|
|
2Минеральный вид
Индицирование
.
16. Закон целых чисел (Гаюи)
Второй закон клисталлографии.
Отношение отрезков, отсекаемых двумя гранями кристалла на координатных осях( или на трех пересекающихся ребрах) относятся друг к другу как целое, взаимно простые и малые числа. Для сравнения между собой параметров граней кристалла одна из его граней принимается за масштабную. Ее называют единичной гранью. При измерении положения других граней изучаемого кристалла параметры это грани принимают за единицу.
17. Закон постоянства двугранных углов(Стено).
Стено закон, закон постоянства углов кристаллов, утверждает, что во всехкристаллах данного вещества при данных температуре и давлении двугранные углы между соответствующими гранями кристаллов (вне зависимости от размеров и формы граней) всегда одинаковы. Установлен Н. Стено в 1669 на основании наблюдения многогранных форм природных кристаллов и объясняется тем, что грани кристаллического многогранника соответствуют плоским атомным сеткам в кристаллической решётке. С. з. лежал в основе классификации и определения кристаллических веществ (измерение углов с помощью гониометра).
18. Трансляции в кристаллических структурах. Принцип построения кристаллической решетки.
Кристалл с определенной химической формулой имеет присущую ему кристаллическую структуру.
Кристаллические структуры - это структуры, представляющие периодическую решетку, в узлах которой расположены атомы. Трехмерная кристаллическая структура представляет решетку, построенную на трех координатных осях x, y, z, расположенных в общем случае под углами a, b, g . Периоды трансляции атомов по осям (параметры решетки) равны, соответственно, a, b, c.В результате трансляции элементарной ячейки в пространстве получается пространственная простая решетка - так называемая решетка Браве. Существует четырнадцать типов решеток Браве. Эти решетки отличаются друг от друга видом элементарных ячеек.
В кристаллической структуре, самосовмещение наступает при переносе вдоль любого трансляционного вектора. Периодичность такого узора описывается трехмерной решеткой — параллелепипедалъиой узловой сеткой, называемой пространственной решеткой .Минимальным представителем трехмерной решетки будет параллелепипед, ребрами которого служат три некомпланарных вектора Ta, Тb и Тc
периоды идентичности вдоль трех узловых рядов решетки. Такой параллелепипед повторяемости, или идентичности, называют также ячейкой трехмерной решетки, которая также без остатка выполняет все трехмерное пространство. Прикладывая решетку к другой заинтересовавшей нас точке при сохранении параллельности решетки самой себе, в ее узлах вновь получим все эквивалентные точки. Тип плоской сетки не зависит от того, какая точка принята за исходную конкретная структура кристалла, т. е. не конкретная укладка атомов (или фигур) в неподвижных узлах решетчатого каркаса, а математический образ — схема, с помощью которой мы описываем периодичность кристаллического вещества, не зависящая от того, какая точка трехмерного пространства (узора) принята за исходный узел. Иными словами, решетку удобно считать своеобразным элементом симметрии, размножающим точки пространства совершенно аналогично тому, как их размножают другие элементы симметрии — плоскости, оси и т. д. В этом смысле решетка — это свойство кристаллического состояния вещества, ибо любое кристаллическое вещество, даже лишенное каких-либо иных элементов симметрии, всегда обладает этим основным элементом симметрии — решеткой, или решетчатым строением.
По определению академика Н. В. Белова, кристалл находится в состоянии решетки. Как каждый единственный в своем роде элемент симметрии допускает только те элементы симметрии, которые переводят его в самого себя, так и решетка допускает присутствие только тех элементов симметрии исходной фигуры, которыми обладает она сама как геометрический образ. Поэтому помимо функции размножения исходной фигуры присущими решетке трансляциями она может рассматриваться и как «инструмент», передающий структуре кристалла (бесконечному узору) симметрию размножаемой конечной фигуры (молекулы, группы атомов). СОна всегда центросимметрична, при этом центры инверсии находятся как в узлах решетки — в вершинах параллелепипедов, так и на серединах расстояний между ними. Кроме того, если в решетке присутствуют оси высшего порядка, то они неизбежно сопровождаются пересекающимися вдоль них плоскостями симметрии. Сами же оси симметрии ограничены только кристаллографическими порядками, т. е. п = 1, 2, 3, 4, 6.
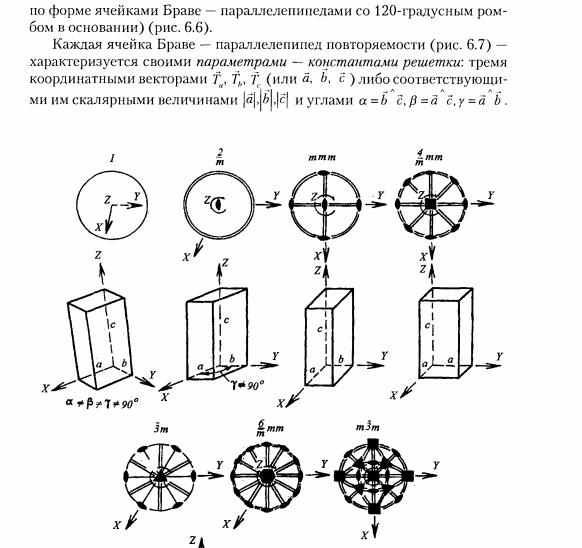
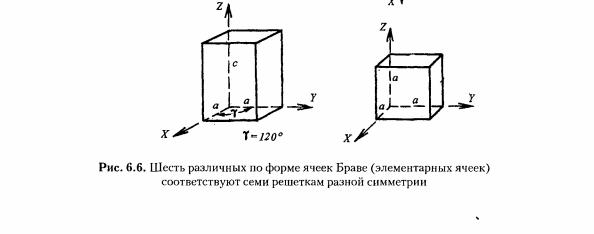
19. Элементарная ячейка (параллелепипед повторяемости) кристаллической структуры, ее параметры и правила выбора.
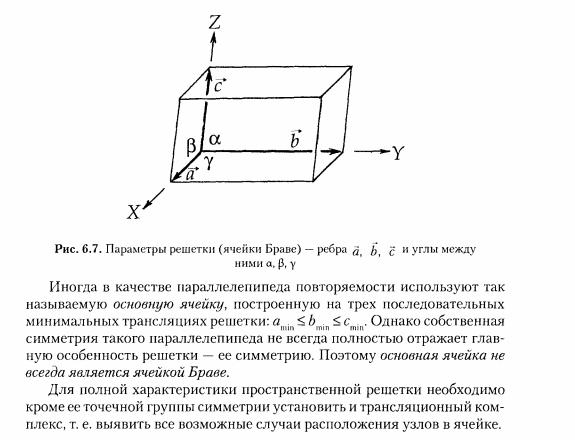
Характеристическая ячейка, наиболее полно отражающая все особенности трехмерной решетки, — это параллелепипед, построенный на трех кратчайших неколлинеарных трансляционных векторах, совпадающих с особыми направлениями максимальной симметрии т. е. с на правлением кристаллографических координатных осей, а при отсутствии особых направлений — с узловыми рядами. Например, в триклин-ной решетке ребра характеристической ячейки рекомендуется совмещать с такими трансляционными векторами, которые обеспечат ее примитивность, а следовательно, минимальный объем. В моноклинной решетке одно ребро ячейки совмещают с единственным особым направлением ( —), а два других ребра направляют по трансляционным векторам, лежащим в плоскости, перпендикулярной этому особому направлению (т. е. в плоскости симметрии решетки, а следовательно, по векторам повышенной симметрии). Отсутствие особых направлений в плоскости косоугольной грани не накладывает ограничений на выбор ребер ячейки, поэтому узлы такой грани будут располагаться только в ее вершинах. Выбранный таким образом параллелепипед подчинен кристаллографической координатной системе, имеет минимальную площадь и называется элементарной ячейкой или ячейкой Браве. Поскольку форму ячейки Браве определяет координатный репер, семь разных по симметрии реше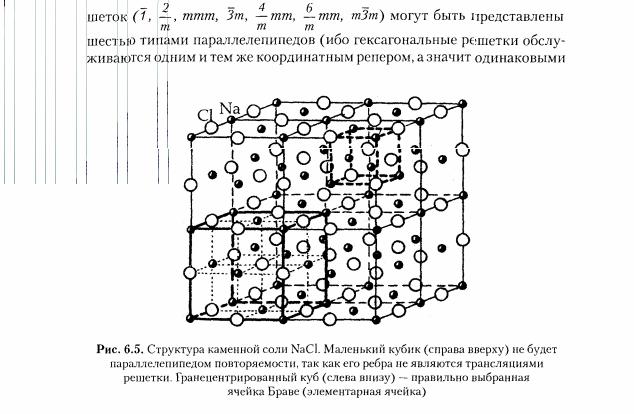
 
20. Решетки Бравэ, их обозначения. Элементы симметрии бесконечных фигур, их сочетания.
БРАВЕ РЕШЁТКИ - классификация решёток параллельных переносов, учитывающая как их точечную, так и параллельно-переноснуюсимметрию. Всего существует 14 типов Б. р., названных по имени О. Браве (A. Bravais), строго обосновавшего эту классификацию. Решёткой наз. совокупность точек пространства (узлов) с целочисленными координатами относительно фиксированной системы координат, построенной на трёх базисных векторах а, b, с - осн. репере решётки. Для представления решёток используют репер Браве - систему координат, построенную на векторах решётки, совпадающих с наиб. симметричными в данной голоэдрии направлениями. Выбор таких векторов может быть неоднозначным и существуют дополнит. правила: сначала выбираются векторы, совпадающие с осями симметрии, затем - самые короткие векторы, не образующие острых углов между собой. Параметры реперов Браве (длины а, 6, с, его векторов и углы 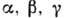 между векторами b и с, а ис, а и b соответственно) в каждой из 7 сингоний (совокупностей решёток с одинаковой голоэдрией) имеют ограничения, указанные в табл., в к-рой также приведены обозначения всех Б. р., распределённые по соответств. сингониям.
|
|
|
|
|
|
|
Сингония
|
Параметры репера Браве
|
Обозначения Браве решёток
|
|
|
международные
|
физические
|
|
|
Триклинная
|
|
|
|
|
|
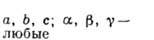
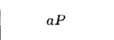
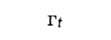
Моноклинная
|
|
|
|
|
|
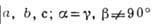
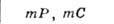
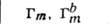
Ромбическая
|
|
|
|
|
|
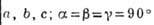
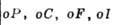
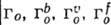
Ромбоэдрическая
|
|
|
|
|
|
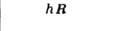
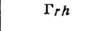
Тетрагональная
|
|
|
|
|
|
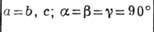
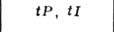
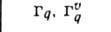
Гексагональная
|
|
|
|
|
|
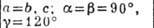
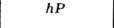
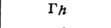
Кубическая
|
|
|
|
|
|
|
|
|
|
|
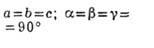
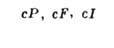
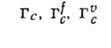
Параллелепипед, построенный на репере Браве, наз. параллелепипедом Браве. Если узлы решётки находятся только в вершинах параллелепипеда Браве, то он и соответствующая ему решётка наз. примитивными (Р-решётки). В нек-рых решётках в параллелепипед Браве попадают дополнит. узлы. Такие параллелепипеды (и решётки) возможны 4 сортов: 1) базоцентрированные С или бокоцентрированные В (А) - дополнит. узлы в центрах граней, построенных на векторах а и b, а и с, b и с соответственно и на параллельных им гранях; 2) дважды центрированные гексагональные (ромбоэдрические) R - дополнит. узлы на главной диагонали параллелепипеда Браве в точках с координатами 2/3, 1/3, 1/3 и 1/3, 2/3, 2/3 ; 3) гранецентрированные F - дополнит. узлы в центрах всех граней параллелепипеда Браве; 4) объёмноцентрированные I - дополнит. узел в центре параллелепипеда Браве.
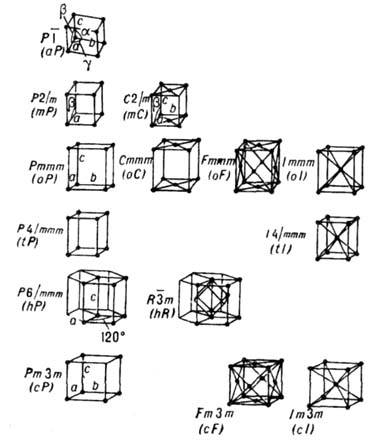
Две решётки относятся к одному и тому же типу Браве, если их параллелепипеды Браве одинаковы и имеют одинаковую центрировку. На рис. представлены все типы Б. р., причём в одной строке расположены решётки с одинаковыми параллелепипедами Браве, а в одном столбце - решётки с одинаковым типом центри-ровок. Около каждого параллелепипеда Браве указан символ соответствующей группы Браве - полной совокупности преобразований симметрии соответствующей решётки. Имеется 14 абстрактно-неизоморфных таких групп (14 из 73 симморфных фёдоровских групп). Группы Браве - основа теоретико-группового определения типов Б. р.: две решётки относятся к одному и тому же типу Браве, если их полные группы преобразований симметрии изоморфны. В скобках на рис. приведены стандартные символы соответствующих типов Б. р. В двумерном случае (в случае плоскости) имеется 5 типов Б. р.: р2, р2тт, с2тт, p4mm, р6тm.
|
|
|
Скачать 7.05 Mb.