2Минеральный вид
 Скачать 7.05 Mb.
|
|
Явление поляризации в кристаллах. Классическим кристаллом, служащим для изучения эффекта является кристалл исландского шпата (  ). Этот кристалл имеет форму параллелепипеда с углами 78˚ и 102˚ (рис. 11.1). При прохождении света через кристалл луч раздваивается. Это явление носит
название двойное лучепреломление. Лучи поляризованы в двух взаимно-перпендикулярных плоскостях. Один из лучей (обыкновенный) имеет для всех направлений одно и то же значение показателя преломления, для другого луча (необыкновенного) показатель преломления зависит от направления луча. Для исландского шпата  . Даже если луч света падает на поверхность кристалла нормально, один из лучей отклоняется (рис.11.2), и если кристалл вращать вокруг направления падающего луча, этот необыкновенный луч вращается тоже. В кристалле исландского шпата есть одно направление, при распространении света вдоль которого оба луча имеют один и тот же показатель преломления (рис.11.3). Это направление – оптическая ось кристалла. Кристалл исландского шпата – одноосный. Существуют кристаллы (двухосные) в которых есть два направления, вдоль которых не происходит двойного лучепреломления. Однако тогда оба луча необыкновенные.Всякая плоскость, проходящая через оптическую ось, называется главным сечениемкристалла (обычно рассматривают главное сечение, содержащее рассматриваемый луч). При двойном лучепреломлении оба луча полностью поляризованы. Терминология (исторически сложилось):плоскостью поляризации называют плоскость, в которой лежит вектор Н. Плоскостью колебаний – плоскость, в которой лежит вектор Е. Если на кристалл падал естественный свет, то интенсивности обоих лучей одинаковы если нет поглощения. Существуют кристаллы, в которых один луч поглощается сильнее другого, например, турмалин. Это явление наз. дихроизм. В турмалине обыкновенный луч практически полностью поглощается уже на глубине 1 мм. 26) Координационные числа и координационные многогранники. Координационным числом данного атома называется число ближайших однотипных соседних атомов (для иона – число ближайших окружающих ионов противоположенного знака). Расположение атомов и число соседей зависят с одной стороны, от отношения их размеров и, с другой от направления и числа связей. В соединениях с ненапрваленой связью на перовм месте стоят соотношения размеров ( катионов и анионов; в металлической связи размеры равны). Число анионов, с которыми может быть одновременно установлен контакт, зависит от относительных радиусов катионов и анионов ( отношения их радиусов) Если ближайшие атомы или ионы соединить линиями, то получится координационный многогранник (полиэдр КП) Координационные многогранники-полиэдры соединяются между собой различными способами: через промежуточные ионы металлов,путем обобществления вершин или ребер. Соединение полиэдров по ребру или грани энергетически невыгодно ( сближение центральных катионов по ребру и возрастание отталкивания их) поэтому редко встречаются. Координационные многогранники вокруг маленьких катионов с более высоким зарядом соединяются только вершинами, с небольшим зарядом- могут ребрами и иногда даже гранями. 27) Пределы устойчивости кристаллических структур (принцип формирования координации). Структура кристалла считается устойчивой лишь в том случае когда каждый ион соприкасается с ионом противоположного знака, при этом одинаково заряженные ионы удалены друг от друга. Предел устойчивости кристаллических структур определяется соотношением радиусов катиона и аниона в момент их касания. Например, соотношение радиусов катиона и аниона у октаэдра =0,41. Это означает что начиная с 0.41 и выше соединение с КЧ=6 будет устойчиво, при этом 0.41 – нижний предел устойчивости таких структур. Верхним пределом устойчивости с КЧ=6 является обратная величина 1:0.41=2.41 28)Теория плотнейших упаковок. Теория плотнейших упаковок шаров обоснована академиком Николаем Васильевичем Беловым. Атомы и ионы каждого элемента характеризуются определенным размером – сферой действия, внутрь пределов, которой не могут проникать другие частицы. В теории шаровых упаковок атомы, анионы и катионы представляются в виде несжимаемых шаров соответствующих радиусов и должны быть упакованы в кристалле максимально плотно. Теория справедлива для ионных, молекулярных и металлических кристаллов, в которых химическая связь ненаправленная и ненасыщенная. АБАБ гексагональнаяплотнейшаяупоковка - ГПУ -2х слойная АБСАБС кубическая п у – КПУ – 3х слойная 29)Структурные единицы кристаллов, структурные формулы минералов. Структурные типы, изоструктурность. В кристаллографии за структурную единицу принимается элементарная ячейка пространственной решетки, которая занимает минимально возможный объем и обладает всеми свойствами трехмерной кристаллической решетки. Элементарная ячейка кристаллической решетки считается определенной, когда известна природа и положение частиц, образующих кристалл, длина ребер a, b, с и величина углов α, β и γ между гранями ячейки (рис. 1). 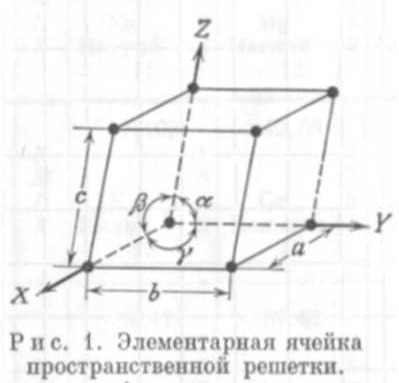 Поскольку химический состав и структура связаны между собой, для выражения этой взаимосвязи используется структурная формула. Хотя структурная формула не дает детальной информации о подлинном пространственном расположении атомов, тем не менее она показывает количество различных катионных и анионных узлов в кристаллической решетке (если имеется только один анион, например кислород, то число узлов часто не указывается). Так, структурная формула минералов группы оливина дается в виде M2SiO4, где M представляет собой двухвалентный катион Fe2+ или Mg. Структурная формула гранатов выглядит как A3B2Si3O12, где А — двухвалентные катионы Ca, Mn2+, Fe2+, Mg, а В — трехвалентные катионы Al, Fe3+, Cr. Если различные атомы занимают позицию в эквивалентных узлах решетки, то в структурной формуле они помещаются совместно в скобках. Например, формула кальцийсодержащего альмандина (группа граната) будет выглядеть как (Fe2+, Ca)3Al2Si3O12, где Fe2+ и Ca занимают одинаковые узлы кристаллической решетки. Наиболее преобладающие в узлах элементы даются первыми, а далее приводятся другие элементы в порядке снижения их количеств. Структурный тип- структуры, одинаковые с точностью до подобия (строго только для кубических кристаллов). Изоструктурность-одинаковый структурный тип при разном химическом составе – галит, галенит.Одна пространственная группа симметрии. *Закон Федорова – Грота: вещества с простым химическим составом обладают более высокой симметрией по сравнению с кристаллами более сложного состава.. 30) Полиморфизм, фазовые переходы, их типы. Политипия. Изоморфизм, его виды. Распад твердого раствора (экссолюция). Полиморфизм – способность твердых веществ образовать при одном химическом составе в разных условиях различные по строению кристаллические структуры и, соответственно, формы кристаллов. Полиморфные модификации имеют собственное название и могут различаться: координационными числами, типом связи, типом ПУ, мотивом расположения катионов, поворотом некоторых структурных элементов, вращением радикалов в кристаллической структуре. Полиморфные переходы:
Политипизм – различная последовательность укладки идентичных слоев в структуре слиостых минералов (слюды, глины) или различные развороты слоев относительно друг друга.(Способность одного и того же вещества кристаллизоваться в нескольких слоистых структурных модификациях, различающихся только поворотом или порядком чередования слоёв.) Обозначение политипов: цифра – количество слоев, буква – симметрия яцейки. Тк – триклинная, М – моноклинная, О-ромбическая,R-ромбоэдрическая. Н-гексаганальная, С – кубическая.SiC- политип 594 R. Изоморфизм:1) свойство химически и геометрически близких атомов, ионов и их сочетаний замещать друг друга в химических соединениях; 2) свойство минералов родственного состава и структуры образовывать ряд смешанных гомогенных минералов одинаковой кристаллической структуры – изоморфные смеси или твердые растворы.
Изоморфизм различается: 1. По типу компенсации валентности - изовалентный и гетеровалентный. 2. По степени совершенства: совершенный и несовершенный. 3. Направленный изоморфизм. 4. По количеству атомов, участвующих в изоморфизме: двухатомный и многоатомный изоморфизм. У некоторых соединений способность к полному замещению двух компонентов при высоких температурах исчезает при охлаждении. При этом охлажденный твердый раствор распадается на исходные фазы. Этот процесс называется распадом твердого раствора экссолюция. Например, щелочные полевые шпаты при высоких температурах смешиваются в неограниченных пределах. Так что любой состав в системе KAlSi3O8 - NaAlSi3O8отвечает гомогенной фазе. Однако при комнатной температуре твердые растворы распадаются на фазы богатого Naи на богатого К-ем полевого шпата. Такие агрегаты называются пертитами. 31) Физические свойства изоморфных примесей. Физические свойства минералов можно объединить в группы: оптические свойства (кристаллооптические и спектроскопические), механические, плотность, электрические, магнитные, вращательные (вращение плоскости поляризации), свойства, связанные с наличием полярных направлений (пиро- и пъезоэлектричество). 32)Анизотропия физических свойств кристаллов. Скалярные, векторные, тензорные физические свойства кристаллов. Анизотропия - зависимость физических свойств вещества от направления.Физические свойства минералов могут описываться скалярными, векторными, тензорными величинами. Анизотропно проявляются в объеме кристалла все физические свойства: оптические, электрические, теплофизические свойства, твердость и др. Скалярные свойства- физические свойства, величина которых не зависит от направления от которого они определяются. Н-р: масса, плотность, теплоемкость, модуль сжатия, температура плавления и др. Ск вел-ы задаются одним числом. Геометрический образ – сфера, симметрия которой - ∞/∞mm. Векторные свойства- физические свойства, величина которых зависит от направления. Твердость спайность и т.д. Симметрия вектр свойства соответствует симметрии неподвижного конуса - ∞mm. Тензорные – направленные физические величины описываемые в некоторой системе координат. Удельная электропроводность, теплопроводность – тензоры 2 ранга Скалярные свойства – тензорные свойства нулевого ранга. Векторные св – тензсв 1 ранга. 33) предельные группы симметрии Кюри. П. Кюри показал, что имеется 7 предельных точечных групп. Симметрия каждой из них наглядно изображается соответствующей геометрической фигурой. 1. Группа , (одна ось симметрии бесконечного порядка). Ей соответствует равномерно вращающийся круговой конус. Группа полярна и энантиоморфна(ЭНАНТИОМОРФИ́ЗМ (от греч. enantios — противоположный и morphe — форма), свойство некоторых кристаллов существовать в модификациях, являющихся зеркальными отражениями друг друга.), потому что конус может вращаться вправо и влево. 2. Группа m, (ось симметрии бесконечного порядка и бесконечное число продольных областей симметрии). Ее символизирует покоящийся круговой конус. Группа полярна, но не энантиоморфна. 3. Группа /m, (ось бесконечного порядка, поперечная плоскость симметрии и центр инверсии). Симметрия группы /m — симметрия вращающегося цилиндра. Торцы цилиндра неодинаковы: с одной стороны торца вращение осуществляется по часовой стрелке, с другой — против. Ось симметрии не полярна, оба ее конца можно совместить друг с другом путем отражения в поперечной плоскости симметрии. 4. Группа 2, (ось симметрии бесконечного порядка и бесконечное число поперечных осей 2). Может быть представлена цилиндром, концы которого закручены в разные стороны. В этой группе возможенэнантиоморфизм. 5. Группа /mmm, (одна ось бесконечного порядка, одна поперечную и бесконечное множество продольных плоскостей симметрии, бесконечное множество продольных осей 2 и центр симметрии). Симметрия этой группы – симметрия покоящегося цилиндра. 6. Группа /, (центр симметрии и бесконечное множество осей бесконечного порядка и плоскостей симметрии). Описывает симметрию обычного шара. 7. Группа /m, (бесконечное множество осей симметрии бесконечного порядка, без плоскостей и центров симметрии). Изображают ее своеобразным шаром, у которого все диаметры закручены по правому или левом винту соответственно правой или левой энантиоморфной формам. 33.Принцип Кюри (диссиметрии /суперпозиции) При взаимодействии нескольких явлений разной природы со своей симметрией сохраняются только общие элементы симметрии. Принцип Кюри можно продемонстрировать на примере сложения двух геометрических фигур, каждая из которых обладает собственной симметрией. В результате сложения диссиметрии составной фигуры увеличилась. 2вар: при наложении нескольких явлений различной природы в одной и той же системе их диссеметрии складываются, то есть кристалл под внешним воздействием изменяет свою точечную симметрию таким образом, что в группе симметрии его внешней формы сохраняются лишь те элементы симметрии, которые являются общими для групп симметрии как самого кристалла так и воздействий взятых отдельно Принцип Неймана. Элементы симметрии каждого физического свойства включают в себя элементы макроскопической симметрии кристалла. Физическое свойство может обладать более высокой симметрией, чем сам кристалл. Связь между точечной симметрии кристалла и симметрии его физических свойств сформулировал Нейман: материал в отношении физических свойств обнаруживает симметрию того же рода, что его кристаллографическая форма(идея изучения физ.свойств с помощью симметрии) Далее ученик Неймана Фойгт уточнил данный принцип: группа симметрии любого физ.свойства должна вкл все элементы точечной группы симметрии кристалла( симметрия физ.свойства не может быть ниже точечной группы симметрии кристалла. Принцип неймана указывает лишь на возможность, но не обязательность проявления определенного физ.свойства у данного кристалла. То есть яв-ся необходимым, но недостаточным условием, используя этот принцип можно, зная группу симмтерии, предсказать физ.свойства., либо зная физ.свойства, установить у кристаллов каких классов симметрии они возможны 34.Оптические свойства кристаллов. Каждое вещество с определенной кристаллической структурой характеризуется своеобразными оптическими свойствами, которое имеет решающее значение при диагностике. Оптические свойства тесно связаны с кристаллической структурой твердого тела, его симметрией. Все вещества можно разделить на изотропные и анизотропные. К первым относятся аморфные тела и кристаллы высшей категории, ко вторым-остальные кристаллы. В оптически изотропных средах световая волна, представляющая собой совокупность поперечных гармонических колебаний электромагнитной природы, распр-ся с одинаковой скоростью во всех направлениях. В оптические анизотропных средах скорости распространения волны в разных направлениях могут быть различны. Оптические постоянные минералов показатель преломления n, коэффициент поглощения k коэффициент отражения R отражательная способность. R=(n-1)2+k2 / (n+1)2+k2 Дисперсия показателей. Оптическая индикатриса Индикатриса- поверхность, построенная на величинах показателей преломления, отложенных в направлении электромагнитных колебаний световых волн. В общем случае – это эллипсоид с тремя различными осями. Индикатрисой кристаллов высшей категории, как и оптически изотропных аморфных тел, будет сфера, то есть в таких кристаллах нет направлений, распространяясь по которым свет испытывал бы двупреломление и для характеристики данной индикатрисы достаточно знать радиус сферы, то есть один показатель преломления. Оптическийиндикатриссой кристаллов средней категории является эллипсиоид вращения в одной главной осью-осью вращения. Показатели преломления кристалла для всех колебаний, совершающих в плоскости кругового сечения,равны.для характеристики эллипсоида вращения достаточно знать половину величины оси вращения эллипсоида и радиус его кругового сечения. Оптический индикатрисой для кристаллов низшей категории является трехосный эллипсоид с тремя взаимно перпендикулярными осями, по величине отвечающим трем разным показателям преломления. Индикатриса имеет 2 круговых сечения с радиусами, равными средней по величине оси эллипсоида, а следовательно 2 оптические оси, то есть имеет 2 направления, распространяясь по которым свет не испытывает двулучпреломления В кристаллах средней категории ось вращения оптической индикатрисы совпадает с главной единственной осью высшего порядка. В ромбических кристаллах с взаимно перпендикулярными осями совпадают также взаимно перпендикулярные оси оптической индикатрисы. В моноклинных лишь одна из осей оптической индикатрисы совпадает с единственным особым направлениием кристалла, а две другие фиксируется относительно выбранной координатной системы, то есть относительно ребер кристалла.В кристаллах триклинной сингонии-кристаллы без особых направлений-все три оси индикатриссы могут быть по-разному ориентированы в кристалле. Оптическая индикатриса кубических кристаллов имеет форму шара. | ||||
