Книга (3). 3. 18. Случайная величина изменяется в пределах от до
 Скачать 1.63 Mb. Скачать 1.63 Mb.
|
|
3.18.* Случайная величина изменяется в пределах от α до β(α<β) по размерному закону. Составить выражение закона ⨈(x) и найти математическое ожидание и дисперсию случайной величины. 3.19.* Показать, что если ⨈(x) является четной функцией, то M(x)=0, а D(x) можно находить по формуле 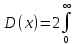 x2⨈(x)dx x2⨈(x)dx3.20.* Найти математическое ожидание и дисперсию случайной величины, имеющей в интервале(- 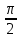 , , 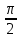 ) распределение по закону ) распределение по закону ⨈(x)= 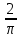 cos2 x; cos2 x;вне указанного интервала ⨈(x)≡0. 3.21.*Найти математическое ожидание и дисперсию случайной величины, имеющей в интервале -1 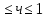 распределение по закону распределение по закону⨈(x)= 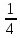 ch b x; ch b x;вне этого интервала ⨈(x)≡0. Коэффициент b также подлежат определению. 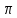 2 23.22.*Пусть известно, что ⨈(X)=⨈(-x) внутри интервала (-𝝅≦x≦𝝅), вне этого интервала ⨈(x)≡0. Показать, что D(x)= 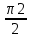 +4 +4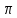 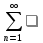 (-1)n (-1)n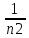 An Anгде An- коэффициенты разложения ⨈(x) и ряд Фурье на заданном интервале. 3.23.* Даны два дискретных распределения(рис. 3.7). x1=1; p1=0.5; x2=1; p2=0.5; y1= 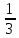 ; p1-0.9; y2=2; p2=0.1. ; p1-0.9; y2=2; p2=0.1.Найти средние значения 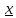 и и 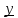 , дисперсии , дисперсии 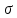 x2 и x2 и 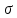 y2 и энтропии Hx и Hy. y2 и энтропии Hx и Hy.3.24.* Определить, при каком числе m значений дискретной случайной величины, имеющей равномерное распределение, энтропия будет равна 1 или 2, если основаниями логарифмов будут служить числа 10, 2 и е. 3.25.* Показать, что при двух событиях с вероятностями p1 и p2 энтропия будет наибольшей при p1 = p2 (p1+p2=1). 3.26.* Задано распределение с вероятностями: p1=0,1; p2=0,1; p3=0,1; p4=0,7. Определить число значений случайной величины, при котором энтропия равномерного распределения будет равна энтропии заданного распределения. 3.27.* Найти характерные значения и построить график функции y=-plnp. 3.28.* Найти энтропию непрерывного равномерного закона 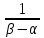 ( (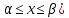 ⨈(x)= { 0 (x  < < 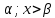 Найти, кроме того, разность между энтропией нормального закона, равной Hнорм=ln( 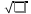 e e 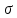 ), ),— 45 — энтропией равномерного закона, у которого было установлено в задаче 3.18, 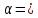 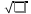 = =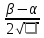 3.29.Дана полная группа, состоящая из двух событий x1 И x2. Вероятность события x1 равна p. Найти характеристическую функцию данной случайной величины. 3.30.*Найти характеристическую функцию распределения Пуассона (2.36) Pm(n)= 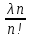 e- e-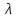 , ,3.31.*Найти характеристическую функцию равномерного закона. 3.34.* Показать, что закон распределения ⨈(x), определяемый при помощи обратного преобразования Фурье через комплексную характеристическую функцию 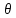 (i (i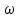 ), Представляет собой вещественную функцию при любом виде ), Представляет собой вещественную функцию при любом виде 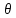 (i (i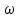 ). ).3.35.*Показать, что где символ * означает сопряженность. 3.36.* Найти первые четыре момента нормального распределения, используя аппарат характеристических функций. Закон нормального распределения принять в виде 3.37.* Показать, что 3.38.* Показать справедливость равенства где 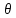 (i (i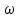 ) - центральные моменты распределения ⨈(x), а ) - центральные моменты распределения ⨈(x), а 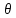 H(i H(i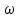 ) - характеристическая функция нормированной случайной величины z, связанной со случайной величиной x равенством ) - характеристическая функция нормированной случайной величины z, связанной со случайной величиной x равенством4. ЗАКОНЫ РАСПРЕДЕЛЕНИЯ И ЧИСЛОВЫЕ ХАРАКТЕРИСТИКИ ФУНКЦИОНАЛЬНОГО ПРЕОБРАЗОВАНИЯ СЛУЧАЙНЫХ ВЕЛИЧИН Задача настоящего раздела формулируется следующим образом, Задан закон распределения случайной величины x в виде ⨈x(x); случайная величина y связана с x детерминированной (неслучайной) функциональной зависимостью y=f(x). Нужно определить закон распределения ⨈y(y) случайной величины y. Частным случаем общей задачи является нахождение числовых характеристик закона ⨈y (y) без определения самого закона. Эти задачи встречаются при изучении прохождения случайных сигналов через линейные и нелинейные цепи ( разд. 10, 11). Сформулированная задача может быть решена как непосредственно, так и на основе аппарата характеристических функций. Начнём с <<непосредственного>> решения. Рассмотрим функцию y=f(x) (рис. 4.1). Вначале положим, обратная функция x= 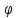 (y), которую будем записывать в виде x(y) - однозначна. Вероятность того, что значение (y), которую будем записывать в виде x(y) - однозначна. Вероятность того, что значение 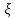 заключено в промежутке x, x+dx, должна быть равна, должна быть равна (вследствие однозначной связи между x и y) вероятности того что значение заключено в промежутке x, x+dx, должна быть равна, должна быть равна (вследствие однозначной связи между x и y) вероятности того что значение 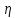 заключено в соответствующем промежутке y, y+dy, т. е. заключено в соответствующем промежутке y, y+dy, т. е.Или Из последнего равенства следует, что причём производную нужно брать по абсолютному значению, так как функция распределения всегда неотрицательна. Введя вместо x обратную функцию x(y), получим: Если функция x= 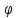 (y) является двузначной (рис. 4.2), т. е. каждому значению y соответствует два значения x, нужно ф-лу (y) является двузначной (рис. 4.2), т. е. каждому значению y соответствует два значения x, нужно ф-лу4.2. Применить дважды: по отношению к каждой ветви кривой x=x1(y) и x=x2(y): Аналогично следует поступать в тех случаях когда функция x(y) - многозначна. Для нахождения числовых характеристик (моментов) закона распределения случайной величины y нет необходимости определять выражение ⨈(у): это можно сделать проще. В самом деле математическое ожидание величины y равно но согласно ф-ле (4.1) для однозначной функции a y=f(x); следовательно, (4.4) Аналогично для начальных и центральных моментов в общем виде получим: В частности, для дисперсии имеем Формулы (4.4) — (4.7) справедливы и для законов, в которых обратная функция х(у) является многозначной. Теперь перейдем к решению общей задачи на основе использования аппарата характеристических функций. Исходя из определения характеристической функции случайной переменной можно ввести понятие характеристической функции случайной величины y, связанной со случайной величиной x зависимостью y=f(x); приняв во внимание ф-лу (4.1), получим Для частного случая линейного преобразования у=ax+b имеем откуда Формула (4.9) представляет собой аналог сочетания известных из теории преобразования Фурье теорема смещения и подобия. По найденной характеристической функции 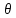 y(i y(i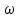 ) можно найти функцию распределения ⨈y(у) либо по таблицам операционного исчисления, либо при помощи обратного преобразования Фурье1): ) можно найти функцию распределения ⨈y(у) либо по таблицам операционного исчисления, либо при помощи обратного преобразования Фурье1):В настоящем разделе первые девять задач посвящены определению законов ?? (у) по ф-лам (4.2) и (4.3), т. е. непосредственно. Задачи 4.10-4.12 содержат условия по определению числовых характеристик закона ??(у) без определения самого закона ⨈y(y). В задачах 4.13-4.15 нужно определить характеристическую функцию 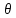 y(i y(i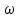 ), а по ней - закон ⨈y(у). ), а по ней - закон ⨈y(у). Задачи и упражнения 4.1.* Найти в общем виде ⨈y(у) по известному закону ⨈x(х) и функциональной связи, выражаемой линейным преобразованием у=ах+b. 4.2.* Найти ⨈y(y), если 4.3.* Найти ⨈y(y), если —— Напомним, что в применяемая здесь преобразовании знак показателя экспоненты противоположен знаку обычного преобразования Фурье(см. разд. 3). 4.4. Найти ⨈y(y), если 4.5.* Найти ⨈y(y), если 4.6.* Найти ⨈y(y), если 4.7.* Найти ⨈y(y), если Решить, далее, ту же задачу, но для закона 4.8.* Найти ⨈y(y), если 4.9.* Найти ⨈y(y), если 4.10*Составить общие выражения для определения среднего значения M(y)=y и дисперсии D(у)=𝜎y2 случайной переменной у по известным соответствующим моментам М(х)= 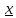 и D(3)= 𝜎y2 случайной переменной х, если случайные переменные связаны между собой линейным преобразованием y=ax+b. и D(3)= 𝜎y2 случайной переменной х, если случайные переменные связаны между собой линейным преобразованием y=ax+b.411.* Составить общие выражения для определения 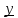 = М(у) и 𝜎y2=D(y) по известным начальным моментам m2x и m1 x , если y=x2 (x>0). = М(у) и 𝜎y2=D(y) по известным начальным моментам m2x и m1 x , если y=x2 (x>0).4.12. Известно, то для рэлеевского распределения четные моменты m2x и m4x равны: Найти математическое ожидание и дисперсия закона распределения случайной величины у, если y=x2(x>0). 4.13.* По известным найти характеристическую функцию 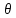 y (i y (i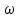 ) закона распределения ⨈y(y), а затем определить ⨈y(y) и по ) закона распределения ⨈y(y), а затем определить ⨈y(y) и по 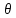 y (i y (i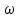 ). Результат проверить, пользуясь ф-лой (4.2). ). Результат проверить, пользуясь ф-лой (4.2). 4.14.* По известным найти характеристическую функцию 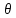 y (i y (i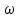 ), а затем ⨈y(y). Результат сопоставить с результатом решения первой части задачи 4.7. ), а затем ⨈y(y). Результат сопоставить с результатом решения первой части задачи 4.7. 4.15.* По известным найти характеристическую функцию 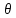 y (i y (i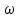 ). а затем ⨈y(y). Результат сопоставить с результатом решения второй части задачи 4.7. ). а затем ⨈y(y). Результат сопоставить с результатом решения второй части задачи 4.7.5. ЗАКОНЫ РАСПРЕДЕЛЕНИЯ СИСТЕМ СЛУЧАЙНЫХ ВЕЛИЧИН Вводные замечания Понятие закона распределения одной случайной переменной (одномерные законы распределения) естественно обобщается на ряд случайных переменных (многомерные законы распределения). Ниже, для простоты изложения, в основном рассматриваются только двумерные законы распределения; определения и формулы, построенные для двух случайных величин, могут быть обобщены на n случайных величин. Содержание материала, посвященного законам распределения двух случайных переменных, можно разбить на следующие разделы: 1. Определения и свойства двумерных законов. 2. Законы распределения суммы независимых случайных величин. 3. Числовые характеристики двумерных законов. Корреляция. 4. Функциональные преобразования двумерных законов. 5. Условные распределения двух случайных величин. Определения и свойства двумерных законов Распределение вероятностей двух случайных величин ________ Индекс 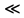 2 2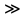 указывает на то, что закон охватывает две случайные переменные. указывает на то, что закон охватывает две случайные переменные.определяет вероятность того, что случайные величины 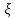 и и 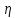 находятся ниже уровней x и y соответственно. находятся ниже уровней x и y соответственно. Если в одномерном случае интегральный закон F(х) даёт ответ на вопрос о расположении точки на прямой, т. е. какова вероятность того, что 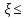 х, то в двумерном случае интегральный закон F2 (х, y) характеризует вероятность того, что точка с координатами х, то в двумерном случае интегральный закон F2 (х, y) характеризует вероятность того, что точка с координатами 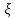 и n (рис. 5.1) находится в заштрихованной части плоскости. и n (рис. 5.1) находится в заштрихованной части плоскости. Ниже приводятся некоторые свойства двумерного интегрального закона распределения. непосредственно следующие из его определения: Двумерная плотность вероятности определяется равенством (5.3) Очевидно (5.4) Подобно тому, как при одномерном законе вероятность того, что точка попадет в заданный интервал на оси, равна площади под кривой ⨈(х), ограниченной указанным интегралом, при двумерном законе распределения вероятность того, что точка попадет в заданную область плоскости хоу, равна объему цилиндра под поверхностью ⨈2 (х, y). основанием которого служит заданная область (на рис. 5.2 она заштрихована). - 52- Вероятность того, что точка будет находиться внутри прямоугольника с вершинами в точках x1y1; x2y1; x2y2; x1y1;(рис. 5.3). навна (см. задачу 5.3) По известной двумерной плотности распределения легко находятся законы распределения каждой из случайных величии. Для случайной величины х имеем1 ) (5.6) где (5.7) Аналогично для случайной величины у (5.8) (5.9) Если имеет место равенство (см. задачу 5.4) (5.10) то случайные переменные являются независимыми. Определением независимости случайных величин может также служить равенство (5.11) Другими словами, две случайные величины независимы, если их совместная функция распределения является произведением индивидуальных функций распределения; справедливо и обратное утверждение. Законы распределения суммы независимых случайных величин Определение закона распределения суммы независимых случайных величин z=x+y по известным законам распределения случайных величин х и y называется композицией законов распределения. 1) Здесь, как и выше (разд. 4), индексы х и у при обозначениях функций ⨈x (x) и ⨈y (y) призваны пояснить, что в общем случае это различные функции. Композиция законов распределения двух независимых случайных величин реализуется на основе применения первой теорем умножения и первой теоремы сложения (разд. 1). Рассмотрим вначале случай дискретных переменных. Текущий индекс переменной х обозначим через i, а переменной у - через j. Для каждой пары значений хi и уi. удовлетворяющей равенству z=x+y, можно написать в соответствии с этим, вероятность того, что случайная величина z будет равна х+у. когда х и у пробегают все значения, удовлетворяющие исходному равенству, составит (5.12а) или, (5.12) Вероятность того, что случайная величина х+у не превзойдет величины z (рис. 5.4), определяется того же вида ф-лами (5.12), но суммирование должно выполняться так, чтобы удовлетворялось соотношение обозначение Р (х+у 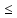 z) в этом случае можно заменить символом, соответствующим интегральному закону, т. е. F(z). Таким образом, z) в этом случае можно заменить символом, соответствующим интегральному закону, т. е. F(z). Таким образом,где yi 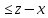 . Обобщим последнее выражение, выполнив суммирование как по хi, так и по уi, (рис. 5.4): . Обобщим последнее выражение, выполнив суммирование как по хi, так и по уi, (рис. 5.4): и, следовательно, можно написать: (5.13) причем хi+ уi 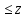 . .При рассмотрении непрерывных случайных переменных нужно совершить соответствующий предельный переход: — 54 — Так как хи у -независимые случайные переменные, то dy можно заменить на dz: Верхний предел в первом интеграле можно заменить на z (а если не возникает неопределенность, и на 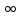 ), так как в левой части нужно найти функцию от переменной z. Совершив эту замену, продифференцируем под знаком интеграла и окончательно получим ), так как в левой части нужно найти функцию от переменной z. Совершив эту замену, продифференцируем под знаком интеграла и окончательно получим (5.14а) Последнее выражение называют сверткой законов распределения.Если закон распределения суммы случайных переменных ⨈z(z) отличается от одинаковых законов распределения каждой случайной переменной ⨈(х) и ⨈(у) только постоянным параметром, то такие распределения называют устойчивыми. Композицию законов распределения, как правило, сравнительно легко реализовать на основе аппарата характеристических функций, так как характеристическая функция суммы независимых Случайных переменных равна произведению характеристических функций каждой переменной (см. задачу 5.11), т. е. (5.146) Для дискретных законов справедливо также аналогичное соотношение, адресованное к производящим функциям [ф-ла (2.6)]: производящая функция суммы m независимых случайных величин равна произведению их производящих функций, т. е. (5. 14в) Числовые характеристики двумерных законов.Корреляция Числовые характеристики двумерных законов строятся по аналогии с числовыми характеристиками одномерных законов с некоторым развитием для тех случаев, когда случайные переменные х и y являются зависимыми (в статистическом смысле - см. ниже) величинами. Средние значения непрерывных случайных величин 1)опреде 1)Определения числовых характеристик законов распределения дискретных случайных величин строятся совершенно аналогично (см. задачу 5.16). |
