Почему нет. 3. Динамика материальной точки
 Скачать 1.89 Mb. Скачать 1.89 Mb.
|
3.7. Принцип относительности ГалилеяЗададим себе вопрос: почему мы, следуя Ньютону, сформулировали принцип инерции Галилея в виде отдельного (первого) закона движения? Ведь он следует из второго закона при равенстве нулю всех действующих на тело сил. Действительно, это так. Но по отношению к какой системе отсчета мы формулируем законы динамики? Среди всех мыслимых систем отсчета эти законы наиболее просто выглядят в так называемых инициальных системах отсчета. Рассмотрим тело, находящееся настолько далеко от других тел, что оно не испытывает никаких воздействий со стороны последних. Такое тело назовем свободно движущимся. Если теперь с таким телом связать систему отсчета, то в ней свободное движение другого тела выглядит наиболее просто: оно будет равномерным и прямолинейным. Это и есть закон инерции, открытый Галилеем. Смысл закона заключается именно в том, что Существует такая система отсчета, в которой свободная материальная точка находится в покое или движется равномерно и прямолинейно. Система отсчета, в которой выполняется первый закон Ньютона, называется инерциальной. Именно для инерциальной системы отсчета мы сформулировали второй закон Ньютона. Инерциальная система отсчета — тоже определенная абстракция, используемая в науке. На практике свободно движущееся тело, равно как и инерциальная система отсчета, могут существовать лишь с большей или меньшей точностью. В огромном большинстве случаев нашу планету можно выбирать в качестве инерциальной системы отсчета (геоцентрическая система). В других случаях, например, для описания движения планет, в качестве таковой выбирается система, связанная с Солнцем (гелиоцентрическая система). Иногда и этого недостаточно, и тогда пользуются системой, связанной со звездами. Итак, первый закон Ньютона постулирует, что существует такая система отсчета, в которой свободная материальная точка находится в покое, или движется равномерно и прямолинейно. Но если существует хотя бы одна инерциальная система, то любая другая система отсчета, движущаяся относительно нее равномерно и прямолинейно, также будет инерциальной. Действительно, установим связь в описании движения той же материальной точки, рассматриваемой относительно двух разных систем отсчета. Пусть дана система отсчета с началом координат в точке 0 и пусть дана другая система отсчета с началом координат в точке 0' (рис. 3.31). 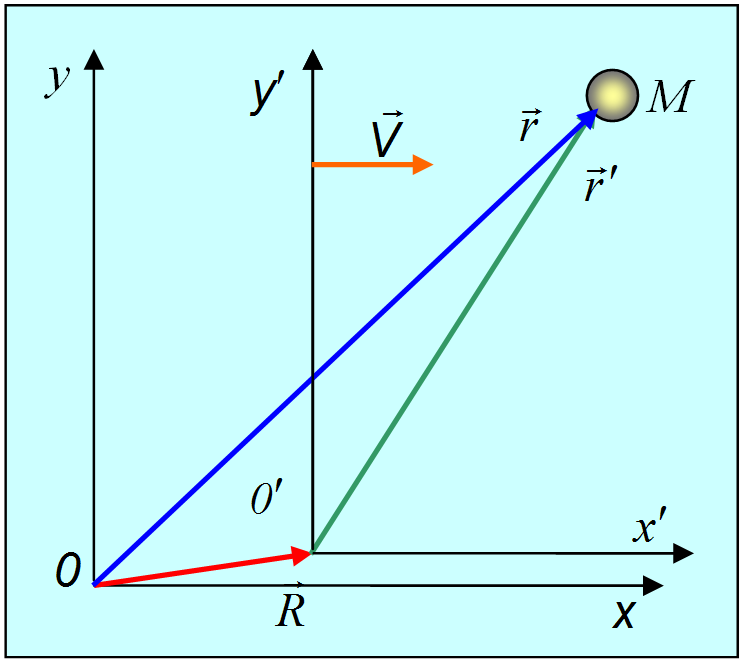 Рис. 3.31. Движение тел в двух разных системах отсчета Все величины, относящиеся к этой системе отсчета, мы будем снабжать знаком штриха (x', y', z' и т.п.). Положение начала отсчета 0' относительно системы 0 характеризуется радиус-вектором . Рассмотрим движение материальной точки М. Ее положение относительно системы 0 задается радиус-вектором , а относительно 0' — радиус-вектором . Исходя из правил сложения векторов, можем написать Дифференцируем данное соотношение по времени и получаем: Здесь , — скорость материальной точки М относительно систем 0 и 0', соответственно. Вектор V — это скорость «штрихованной» системы отсчета относительно «нештрихованной». Мы получили закон сложения скоростей классической механики: Скорость v точки относительно системы 0 может быть представлена как векторная сумма ее скорости относительно системы 0'и скорости V системы 0' относительно системы 0. Если система 0' движется относительно 0 прямолинейно и равномерно, то V не зависит от времени. Дифференцируя полученный закон сложения скоростей по времени, находим, что ускорения точки М относительно обеих систем отсчета одинаковы: Если , то и , то есть закон инерции Галилея выполняется в обеих системах отсчета. Стало быть, если система 0инерциальная, то инерциальной будет и система 0'. Законы механики имеют одинаковый вид во всех инерциальных системах отсчета, которые являются физически эквивалентными (не отличимыми друг от друга). Это и составляет принцип относительности Галилея: Уравнения, выражающие законы природы, инвариантны по отношению к преобразованиям координат и времени от одной инерциальной системы отсчета к другой. Одинаковость вида уравнений движения во всех инерциальных системах отсчета не означает, разумеется, что одно и тоже движение выглядит одинаково в любой инерциальной системе, так как кроме уравнений движения (законов Ньютона) закон движения тела определяется также начальными условиями, которые, в движущихся относительно друг друга инерциальных системах отсчета, естественно, различны: начальные скорости разные Если начальные условия различны, то одно и то же движение тела выглядит по-разному в различных инерциальных системах отсчета. В качестве примера рассмотрим падение мячика с верхушки мачты корабля (рис. 3.32). С точки зрения наблюдателя на корабле мячик движется прямолинейно: падает с нулевой начальной скоростью по вертикали вниз. В то время как для наблюдателя, находящегося на берегу, траектория мяча — парабола: мячик имеет отличную от нуля горизонтальную начальную скорость. 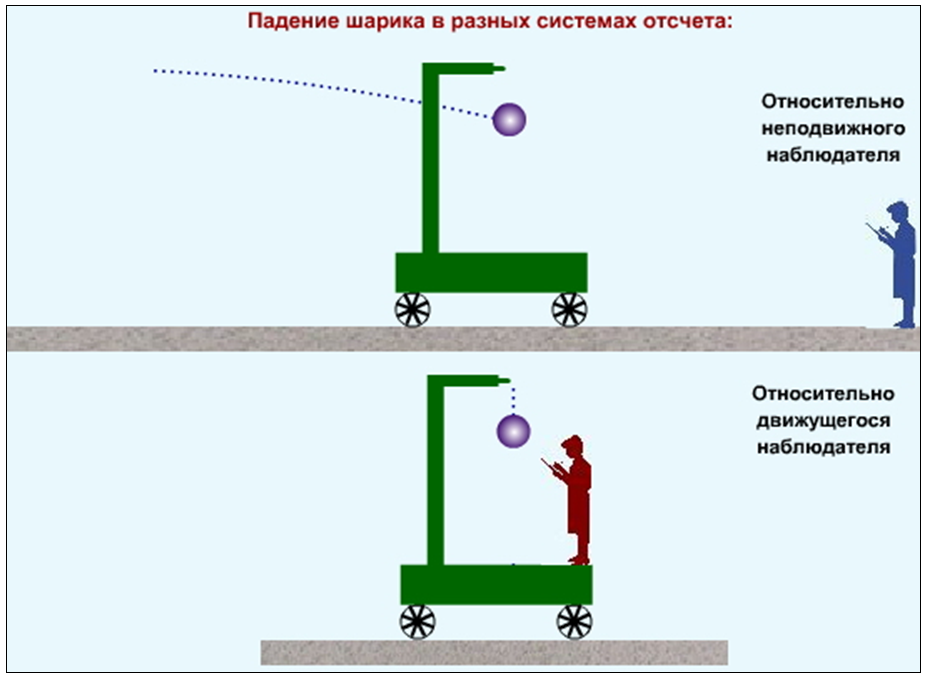 Рис. 3.32. Движение тела в разных инерциальных системах отсчета Связь координат точки в разных системах отсчета дается полученным выше уравнением Его можно записать в виде уравнений для компонент вдоль осей координат. Для упрощения формул часто поступают следующим образом. Во-первых, оси систем выбираются параллельными, причем ось х указывает направление движения системы 0' относительно системы 0. Во-вторых, за начало отсчета времени выбирают момент, когда совпадали начала координат обеих систем. Тогда и мы получаем преобразования Галилея 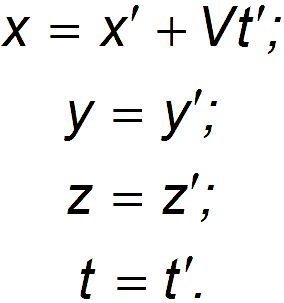 Мы дополнили преобразования пространственных координат равенством времен в обеих системах отсчета, чтобы подчеркнуть, что в классической механике время предполагается абсолютным, оно одно и то же в обеих системах отсчета. Переход в другую систему отсчета — один из методов решения ряда физических задач. Приведем пример. Пример. Катер, двигаясь вниз по реке, обогнал плот в пункте А. Через время после этого он повернул обратно и затем встретил плот на расстоянии ниже пункта А. Найти скорость течения, если скорость катера относительно воды постоянна. В данной задаче рассматривается одномерное движение частиц (плот и катер можно рассматривать как частицы, поскольку они движутся поступательно). Задачу целесообразно решить двумя способами, отличающимися выбором системы отсчета. Способ 1. В системе отсчета, связанной с берегом реки (рис. 3.33), необходимо выразить пути, пройденные плотом и катером, через скорость течения реки и катера относительно воды и времена движения катера вниз и вверх по течению соответственно. После необходимых преобразований становится ясно, что и , следовательно, общее время движения катера, (а, следовательно, и плота) равно . Очевидно, что за это время плот прошел расстояние 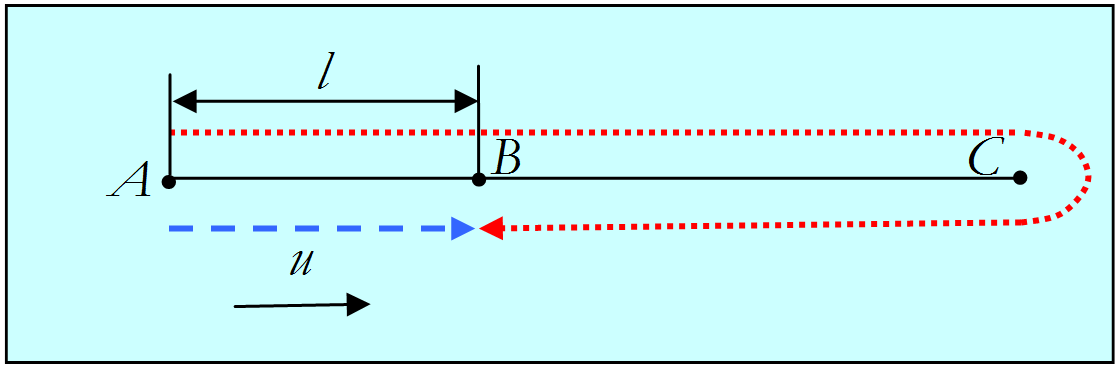 Рис. 3.33. Движение катера вниз и вверх по течению реки В системе отсчета, связанной с берегом, путь , пройденный плотом, равен а путь Учитывая, что после преобразований получаем Следовательно, время движения плота равно , откуда скорость течения Способ 2. В системе отсчета, связанной с плотом, который относительно берегов движется со скоростью течения реки, очевидно, что время движения катера вниз и вверх по течению одинаково, и равно . Поэтому общее время движения равно , и мы вновь получаем тот же результат но гораздо более простым путем. Сопоставление двух способов решения показывает важность обоснованного выбора системы отсчета. |
