Почему нет. 3. Динамика материальной точки

• Название: 3. Динамика материальной точки
• Анкор: Почему нет
• Дата: 11.11.2020
• Размер: 1.89 Mb.
• Имя файла: 02_Dinamika_materialnoi_774_tochki.docx
• Тип: Закон; #149643
• страница: 1 из 5

3. Динамика материальной точки

Динамика исследует законы и причины, вызывающие движение тел, то есть изучает движение материальных тел под действием приложенных к ним сил. Механика — одна из древнейших наук, развитие которой стимулировалось практикой, нуждами общества. К первым теоретическим трактатам по механике относятся «Физика» и «Механика» Аристотеля (IV в. до н.э.). Научные основы статики (теория рычага, учение о центре тяжести, начала гидростатики) разработал Архимед (III в. до н.э.). Дальнейшее развитие механики (сложение сил по правилу параллелограмма, учение о моменте силы) связано с именами итальянца Леонардо да Винчи(ХV в.), фламандца Симона Стевина (ХVI в.) и других ученых. Основу современной классической механики составляют три закона Ньютона. Механика Ньютона базируется на основополагающих принципах Галилея.

3.1. Принцип инерции Галилея

Г. Галилей (1564–1642) справедливо считается основателем физики как науки. Ему мы обязаны развитием современного метода исследований, кратко выражающегося в цепочке: эксперимент => модель (выделение в явлении главных особенностей, то есть применение абстракции) => математическое описание => следствия модели => новый эксперимент для их проверки.

Среди прочих научных достижений, в механике им были введены два основополагающих принципа: принцип инерции и принцип относительности. Принцип инерции Галилея был повторен И. Ньютоном (1643–1727) в качестве первого закона механики.

Первый закон Ньютона гласит:

Существуют такие системы отсчета, в которых всякая материальная точка находится в состоянии покоя или равномерного прямолинейного движения до тех пор, пока это состояние не будет изменено воздействием со стороны других тел. Такие системы отсчета принято называть инерциальными.

Ответ на вопрос: «Существуют ли инерциальные системы отсчета или нет?», как всегда, дает эксперимент. По результатам современных измерений гелиоцентрическая система отсчета, в которой неподвижен центр Солнца, и оси которой направлены на неподвижные звезды, является инерциальной. Это означает следующую простую вещь: существующие акселерометры (измерители ускорения) не обнаруживают отклонений от первого закона Ньютона в гелиоцентрической системе отсчета. Покой или равномерное прямолинейное движение — это состояние с равным нулю ускорением, следовательно, если тело, не подверженное воздействиям извне, приобретает ускорение, то это означает, что движение этого тела рассматривается в неинерциальной системе отсчета. Солнечная система совершает финитное движение в пределах нашей галактики (Млечный путь), любое финитное движение есть движение с ускорением, но солнечная система далека от центра галактики — мы периферийные жители — кривизна её траектории ничтожна, наши приборы не обнаруживают ускорений и мы утверждаем, что гелиоцентрическая система отсчета инерциальна. Инерциальная система отсчета — ещё одна идеализация: в точном смысле инерциальных систем отсчета не существует. Естественно предположить, что это обстоятельство было в ряду тех, что подвигли Эйнштейна на создание общей теории относительности, в которой утверждается физическое равноправие всех вообще, а не только инерциальных, систем отсчета, а поля сил инерции эквивалентны гравитационным полям (так называемый «принцип эквивалентности» подробнее речь об этом пойдет позже).

В дальнейшем будет видно, что любая система отсчета, движущаяся поступательно с постоянной по величине и направлению скоростью относительно некоторой инерциальной системы отсчета, также инерциальна. Другими словами, существование одной инерциальной системы отсчета означает существование бесконечно большого числа таких систем.

Свойство тела сохранять состояние покоя или прямолинейного равномерного движения называется инерцией. Сам этот принцип — принцип инерции Галилея (или первый закон Ньютона) — далеко не столь очевиден.

До Галилея думали, что для движения нужна какая-то причина, движущая сила. Даже великий Леонардо да Винчи писал: «Всякое движение стремится к своему сохранению, или же каждое движущееся тело движется постоянно, пока в нем сохраняется действие его двигателя». Удивительно, но туповатый полковник фон Циллергут из книги Я. Гашека «Похождения бравого солдата Швейка», мыслил похоже: нет бензина, не работает двигатель, автомобиль останавливается. После Галилея стала возможной чеканная латинская формулировка Р. Декарта (1596–1650): «Quod in vacuo movetur, semper moveri» (что движется в пустоте, будет двигаться всегда).

Дело в том, что в природе действительно никогда не наблюдаются тела, вечно сохраняющие состояние покоя или прямолинейного равномерного движения. Нужно было проявить ту самую способность строить модели, отбрасывать несущественное, абстрагироваться, чтобы открыть принцип инерции. Изучая основные законы механики, мы идеализируем систему: пренебрегаем силами трения, считаем, что поблизости нет других тел и т. д. И тогда принцип инерции проявляет себя во всей своей красе и силе:

Для равномерного прямолинейного движения не нужно двигателя, движущая сила нужна для изменения такого вида движения тела.

3.2. Второй и третий законы Ньютона

Для описания воздействия вводят понятие силы. Под действием сил тела либо изменяют скорость движения  , то есть приобретают ускорения (динамическое проявление сил), либо деформируются, то есть изменяют свою форму и размеры (статическое проявление сил). В каждый момент времени сила характеризуется числовым значением, направлением в пространстве и точкой приложения.

Сила — результат и проявление взаимодействия. Это векторная величина,являющаяся в классической(не квантовой) физике количественной характеристикой взаимодействия.



Рис. 3.1. Сила, действующая на пружину

Для того, чтобы установить, какие силы действуют на тело, необходимо определить, с какими другими телами взаимодействует данное тело. Сила всегда есть результат взаимодействия физических тел. Наверное по этой причине Р. Фейнман в своих «Фейнмановских лекциях по физике» назвал силы инерции, не являющиеся результатом взаимодействия рассматриваемого тела с другими телами и появляющиеся только в неинерциальных системах отсчета, псевдосилами.

Видео 3.2. Для того, чтобы выяснить, какие силы действуют на тело, необходимо установить, с какими телами оно взаимодействует. «Знаменитая» задача о соскальзывании тела с наклонной плоскости.

Из опыта известно, что при одинаковых воздействиях различные тела неодинаково изменяют скорость своего движения, то есть, иными словами, приобретают различные ускорения, поэтому в уравнение, связывающее силу, действующую на тело, и его ускорение должна входить некоторая характеристика самого тела. Такой характеристикой является масса тела m.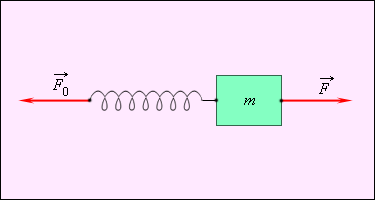



Рис. 3.2. Две различных силы, действующих на тело, вызывают его ускорение.

Установленный экспериментально второй закон Ньютона утверждает:

Произведение массы материальной точки на её ускорение равно векторной сумме сил, приложенных к этой точке:





Рис. 3.3. Несколько сил, действующих на тело, могут нейтрализовывать друг друга.

Сразу подчеркнем, что это справедливо только при нерелятивистских скоростях движения, то есть скоростях малых по сравнению со скоростью света в вакууме:  .

Второй закон Ньютона нередко формулируется так. Произведение массы тела на его ускорение равно векторной сумме сил, приложенных к телу.

Видео 3.3. Взаимодействие тележек: второй и третий законы Ньютона.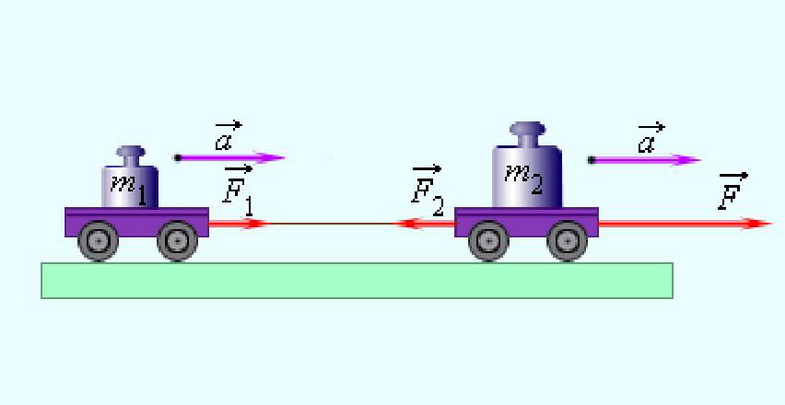



Рис. 3.4. Только внешние силы вызывают ускорение системы (в данном случае — две тележки с грузами.)

Необходимо оговорить, что в такой формулировке, если речь идет о протяженном теле, которое нельзя считать материальной точкой, второй закон Ньютона описывает только поступательное движение протяженного тела, при котором все точки тела имеют одинаковые ускорения, скорости и перемещения. Вращательное движение тела в таком виде — второй закон Ньютона описать не в состоянии. Вращение протяженного тела кардинальным образом зависит от того, в каких его точках приложены силы к телу. Очевидно, что в случае материальной точки этот вопрос лишен смысла: все силы приложены к этой точке. В написанном выше уравнении, а именно:



нет никаких указаний на то, каковы точки приложения сил к протяженному телу.



Рис. 3.5. Движение катушки зависит не только от приложенных сил, но и точек их приложения.

Для описания вращательного движения протяженного тела написанное выше уравнение второго закона Ньютона модифицируется так, чтобы в нём в явном виде присутствовали радиус-векторы точек приложения сил. В результате такой модификации в правой части уравнения вместо сил появляются моменты сил.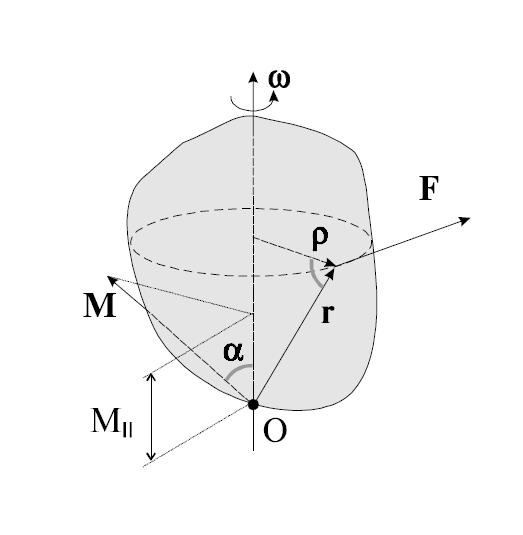



Рис. 3.6. Вращение тела вокруг неподвижной оси.

Учитывая, что ускорение  , второй закон Ньютона можно записать в виде трех полностью

эквивалентных друг другу соотношений:



(3.2.1)



(3.2.2)



(3.2.3)

каждое из которых позволяет подчеркнуть какой-то из аспектов этого закона.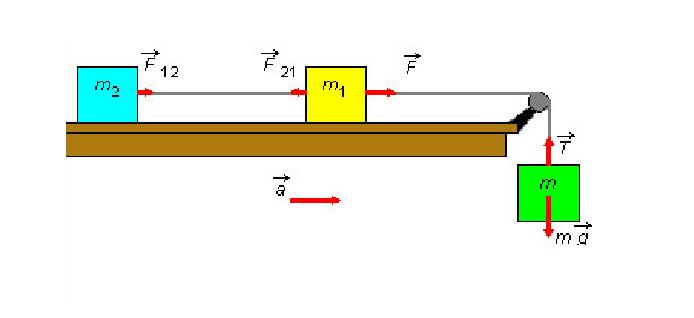



Рис. 3.7. Силы,возникающие при ускоренном движении системы.

Начнем с достаточно тривиальных обстоятельств.

Если для краткости, стоящую в правой части векторную сумму сил   обозначить 

и вспомнить, что сила может быть нестационарной, то есть зависеть от времени, что в большинстве случаев силовые поля неоднородны, то есть сила зависит от координат точки и, что есть такие силы, как например, сила жидкого трения, которая зависит от скорости движения тела в жидкости, то получается, что в общем случае  .

Тогда, из (3.2.3) вытекает, что



(3.2.4)

уравнение второго закона Ньютона есть дифференциальное уравнение второго порядка, разрешенное относительно старшей (второй) производной.

Именно по этой причине уравнение второго закона Ньютона чаще всего называют уравнением движения.

Математики доказали, что, во-первых, при определенных требованиях к свойствам функции, стоящей в правой части уравнения — силе   — решение уравнения (3.2.4) существует. Отметим, что в физических приложениях эти требования практически всегда выполнены, а если нет, то есть смысл проверить, корректна ли, не слишком ли идеализирована постановка физической задачи. Во-вторых, решений уравнения (3.2.4) бесконечно много и отличаются эти решения значениями двух (уравнение второго порядка) векторных констант, для нахождения которых необходимы начальные условия: необходимо указать начальное положение точки и её начальную скорость в некоторый начальный момент времени t₀



(3.2.5)

В математике доказано, что решение дифференциальной задачи (3.2.4) — (3.2.5) единственно. Доказанная единственность решения весьма полезна с чисто практической точки зрения: как бы не была найдена функция, обращающая в тождество уравнение (3.2.4) и удовлетворяющая начальным условиям (3.2.5) — это то единственное решение, которое имеет данная задача.

Запись второго закона Ньютона в виде (3.2.2) подсказывает введение новой кинематической характеристики движущейся материальной точки, учитывающей не только её скорость  , но и массу m. Если масса постоянна, а это именно так — читайте дальше, то её можно ввести под знак производной и переписать уравнение движения в виде



(3.2.6)

Здесь

(3.2.7)

по определению по определению, есть импульс материальной точки массы m, движущейся с нерелятивистской скоростью  , последнее означает (напомним), что  .

Релятивистские ограничения применимости ньютоновской механики вообще, и выражения для импульса (3.2.7), в частности, были поняты, разумеется, не во времена Ньютона, а только после создания Эйнштейном специальной теории относительности, которую в данном контексте, разумеется, можно трактовать как механику околосветовых скоростей, когда  .

На сегодняшний день (начало 2010 года) исчерпывающего ответа на вопрос, что такое масса не существует. Для решения, в частности и этого вопроса, был построен и ныне испытывается в действии БАК — большой адронный коллайдер.

Сегодня, для наших ограниченных целей, можно утверждать следующее.

Масса — феноменологическая характеристика элементарных частиц, не зависящая от того, движется или покоится частица в данной системе отсчета. Другими словами, масса, как, например, и электрический заряд — ни от чего не зависящее число, характеризующее элементарную частицу. Масса, если она отлична от нуля, количественно характеризует инертные и гравитационные свойства тела. Но, не всё так просто, например, масса фотона равна нулю, но фотон участвует в гравитационном взаимодействии: его «траектория» искривляется в гравитационном поле Солнца, что наблюдено, измерено и результат соответствует предсказаниям общей теории относительности.

В основу общей теории относительности положен, так называемый, «принцип эквивалентности», утверждающий, что масса инертная равна массе гравитационной. Другими словами, нет отдельно инертной массы и отдельно массы гравитационной, есть просто масса "ответственная" за всё. Тот факт, что инертная и гравитационная массы строго пропорциональны друг другу было экспериментально установлено венгерским физиком Этвешем (серия экспериментов 1889–1908 годов) с относительной погрешностью не больше  . После этого равенство инертной и гравитационной масс уже не проблема и обеспечивается соответствующим выбором единиц измерения. Результаты экспериментов Этвеша были использованы Эйнштейном при формулировании принципа эквивалентности.

Необходимо признать и принять, что в рамках нерелятивистской ньютоновской механики внятно ответить на вопрос, что такое масса, невозможно. Для этого необходимы представления и средства и специальной и общей теорий относительности, но и их не вполне хватает, ввиду отсутствия на сегодняшний день законченной теории элементарных частиц. Это, впрочем, не привносит никаких трудностей в практическое использование ньютоновской механики.

В системе СИ единицей массы является килограмм (кг). Эта единица измерения является основной.

На рис. 3.8 показаны значения масс некоторых физических объектов.

Рис. 3.8. Массы некоторых физических объектов

Отметим, что если определить энергию E как интеграл движения, сохранение которого у замкнутой системы обусловлено однородностью времени, а импульс   как интеграл движения, сохранение которого у замкнутой системы обусловлено однородностью пространства, то масса есть инвариантная величина, равная



(3.2.8)

Здесь c — скорость света в вакууме, инвариантность которой экспериментально установлена в опытах Майкельсона, Майкельсона и Морли и многочисленных последователей: эксперименты повторялись в течение почти 50 лет (1881 по 1930 год) и, при многократно возраставшей (до 200 раз) точности, дали один и тот же результат. Инвариантность c есть основной постулат специальной теории относительности.

Как уже было сказано структура левой части второго закона Ньютона, записанного в виде (3.2.2) лишь подсказывает выражение для импульса. В действительности можно показать, что как в нерелятивистском так и в релятивистском случаях выражения для импульса (3.2.7) и (3.2.9) являются прямым следствием такого определения импульса:

Импульсом   называется сохраняющаяся характеристика замкнутой системы, сохранение которой обусловлено однородностью пространства. Отсюда для одной нерелятивистской   частицы следует, что её импульс:

Отметим также, что уравнение движения, записанное в виде (3.2.6) с импульсом из (3.2.9) в отличие от (3.2.2) справедливо при любых скоростях.

Уравнение движения в форме (3.2.6)



(3.2.10)

с импульсом   можно прочитать так:

Скорость изменения импульса тела равна векторной сумме сил приложенных к телу.

Нередко весьма полезной оказывается и такая, следующая из (3.2.10), формулировка:

Приращение импульса тела за некоторое время   равно произведению средней суммарной силы, действующей на тело, на время её действия:



Второй закон Ньютона устанавливает единицу измерения силы  .

В системе СИ единицей силы является ньютон (H):

1 ед. силы СИ = 1 ед. массы СИ • 1 ед. ускорения СИ = 1 кг • 1 м/с² = 1 H.>>

Дополнительная информация

http://www.plib.ru/library/book/17005.html – Стрелков C.П. Механика Изд. Наука 1971 г. – стр. 73–75: опыт с обрывом нитей, привязанных к массивному шару сверху и снизу;

http://vivovoco.rsl.ru/VV/JOURNAL/NATURE/10_99/HOOK.PDF — журнал Природа 1999 г. №10 — закономерности удара в механических системах (А.П. Иванов)

Как уже отмечалось, сила не обязана быть постоянной: она может зависеть от времени, от положения тела в пространстве, от его скорости. Поэтому решение уравнения движения в общем случае — достаточно непростая задача. Приведем пример решения такой задачи.

Пример. На покоящееся в начале координат тело массой m в момент времени t = 0 начинает действовать периодическая сила



где   — орт оси 0х, а Т — период изменения силы. Половину периода сила направлена вдоль положительного направления оси 0х, следующую половину периода — в противоположную сторону. Найти зависимость от времени скорости частицы и ее положения (координаты) на оси 0х.

Поскольку максимальное значение силы равно   введем обозначение для максимального ускорения



Тогда уравнение движения примет вид:



Отсюда скорость в момент времени t, с учетом того, что в начальный момент времени частица покоится  , равна



Положение тела на оси 0х также определяется интегрированием. Учитывая, что в начальный момент времени частица находится в начале координат (x(0) = 0), получаем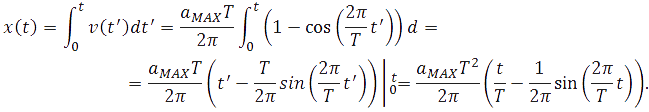



Графики зависимостей от времени ускорения (в единицах  ), скорости (в единицах  ) и координаты (в единицах  ) показаны на рис. 4.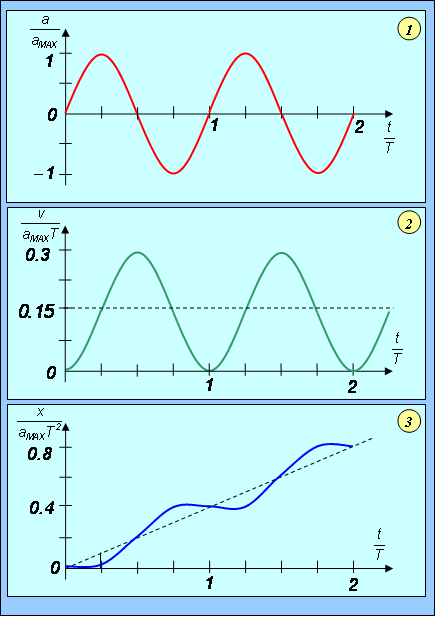



Рис. 3.9. Зависимость ускорения (1), скорости (2) и положения (3) частицы от времени

График ускорения, естественно, повторяет график силы. Скорость изменяется с тем же периодом, что и сила и ускорение, но, в отличие от силы и ускорения, нигде не меняет знака: скорость, набранная за время полупериода положительной силы  , снижается до нуля за время действия отрицательной   силы. Среднее за период значение координаты   растет пропорционально времени. Сама координата осциллирует около этой линейной зависимости. Среднее за период значение скорости постоянно и равно



оно показано пунктиром на рис. 3.9. (2). Зависимость от времени средней координаты показана пунктиром на рис. 3.9. (3).



Рис. 3.10. Несколько сил, действующих на тело.

Как быть, если на нашу точку действует не одна сила, а несколько. В механике большое значение имеет принцип независимости действия сил:

Если на материальную точку действуют одновременно несколько сил, то каждая из них сообщает материальной точке ускорение согласно второму закону Ньютона, не зависящее от других сил.

Полное же ускорение тела равно сумме этих «частичных» ускорений. Согласно этому принципу, силы и ускорения можно разлагать на составляющие, использование которых приводит к существенному упрощению решения задач:

где





и

Сумму сил F называют равнодействующей (или результирующей) силой, приложенной к телу.

Дополнительная информация

http://kvant.mirror1.mccme.ru/1990/02/razmyshleniya_o_masse.html — Журнал «Квант» – из истории физики — размышления о массе (Я. Смородинский);

http://www.plib.ru/library/book/17005.html – Стрелков С.П. Механика Изд. Наука 1971 г. – стр. 102–109: примеры решения задач с применением уравнения Мещерского, формула Циолковского;

http://www.teormex.net/knigi.html# — Тарг С.М. Краткий курс теоретической механики, Изд. Высшая школа, 1995 г. – § 80–81 — излагается методика решения задач динамики прямолинейного движения материальной точки с интересными примерами;

http://ufn.ru/ufn94/ufn94_5/Russian/r945c.pdf – журнал УФН – замечание к §39 учебника Матвеева А.Н. Механика и теория относительности (изд. 2003 г.), об особенностях движения заряженных нерелятивистских частиц в переменном поле плоской электромагнитной волны (Б .Болотовский, А. Серов).

Третий закон Ньютона утверждает, что

Действие тел друг на друга всегда носит характер взаимодействия. Силы, с которыми взаимодействуют тела, равны по величине, противоположны по направлению и направлены вдоль одной общей прямой.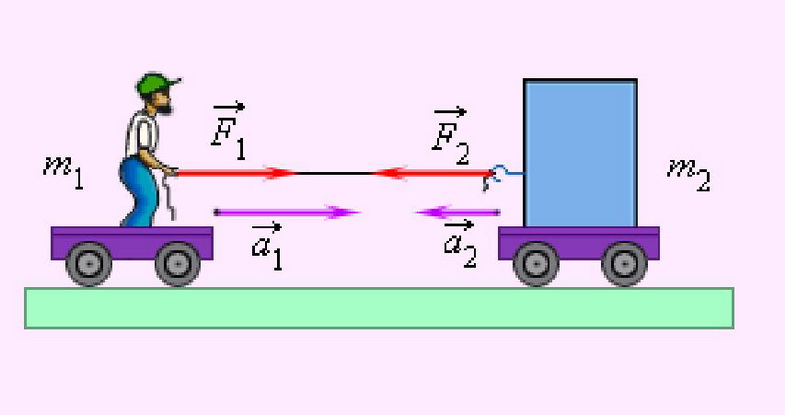



Рис. 3.11. Иллюстрация равенства сил 

Видео 3.4. Расталкивание тележек взрывом: третий закон Ньютона.

Если силу, действующую на первое тело в результате его взаимодействия со вторым телом обозначить   (первый индекс — номер того тела, на которое действует сила), а силу, действующую на второе тело в результате его взаимодействия с первым телом, соответственно  , то равенство сил по величине и их противоположность по направлению можно записать в виде

(3.2.11)

Или, что то же самое:



(3.2.12)

Две равные по величине и противоположно направленные силы образуют, как говорят, «пару сил». Тот факт, что силы взаимодействия, согласно третьему закону Ньютона, направлены вдоль одной общей прямой можно сформулировать так: плечо a пары сил взаимодействия равно нулю. Сказанное поясняет нижеследующий рисунок. Согласно третьему закону Ньютона левая (на рисунке) ситуация а) имеет место, правая — в) невозможна.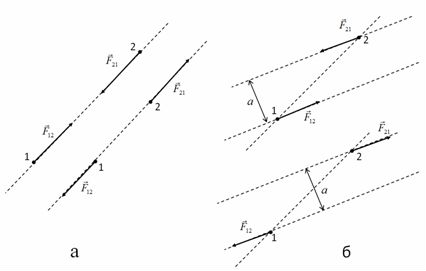



Рис. 3.12. Различные примеры приложения сил.

Если бы два тела составляющие в совокупности замкнутую систему могли взаимодействовать так, как показано в правой — в) части рисунка, то такая замкнутая система сама себя раскручивала бы, что противоречит закону сохранения момента импульсаи чего в эксперименте никто никогда не видел. А если бы не выполнялось соотношение (3.2.12), то такая замкнутая система сама себя ускоряла бы, что противоречит закону сохранения импульса и чего также в эксперименте никто никогда не видел.

Отметим, что в простейшем случае двух покоящихся частиц, имеющих только скалярные характеристики, такие как масса, электрический заряд и тому подобное, третий закон Ньютона является вполне очевидным следствием однородности и изотропии пространства для замкнутой системы. В этом случае единственное физически выделенное направление в пространстве это направление единичного вектора   параллельного прямой, проходящей через те точки пространства, в которых покоятся частицы. Соответственно, силы взаимодействия могут быть направлены только по или против  .



Рис.3.13. Направление силы взаимодействия двух материальных точек.

Однако закон равенства действия и противодействия выполняется лишь в предположении о бесконечной скорости распространения сигналов. Даже в простейшем случае электро-магнитного взаимодействия третий закон Ньютона соблюдается только в пределе   В качестве примера рассмотрим взаимодействие двух положительных зарядов Q₁ и Q₂ (Q₁ > 0; Q₂ > 0), движущихся соответственно со скоростями v₁ и v₂ , на каждой из которых со стороны другого заряда действуют силы F₁ и F₂ (Рис. 3.14)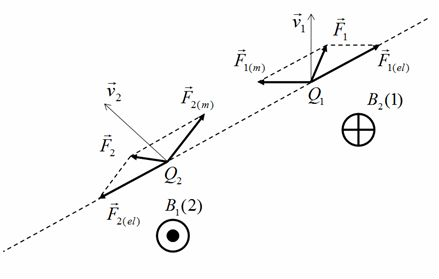



Рис.3.14. Электромагнитное взаимодействие движущихся зарядов (В этом случае третий закон Ньютона не выполняется, т.к. заряды не являются изолированной системоу. В этом взаимодействии участвуют также и поля E и H).

Каждую из этих сил F₁ и F₂ можно предоставить в виде двух составляющих. Первая составляющая есть сила электрического взаимодействия по закону Кулона. Она действует по линии, соединяющей заряды, F_1(el) = –F_2(el) и удовлетворяет требованиям третьего закона Ньютона. Но кроме электрического взаимодействия зарядов существует их магнитное взаимодействие: каждый из движущихся зарядов в точке нахождения другого заряда создаёт магнитное поле с индукцией B. Магнитное поле действует на заряд, движущийся со скоростью v, с силой Лоренца, направленной перпендикулярно скорости.

В ситуации, изображенной на рис. 3.14, поле B₁, создаваемое зарядом Q₁ в точке нахождения заряда Q₂, направленного перпендикулярно плоскости рисунка к нам, а поле B₂, создаваемое зарядом Q₂ в точке нахождения заряда Q₁, направленного перпендикулярно плоскости чертежа от нас. Магнитная сила Лоренца, перпендикулярна скорости v и магнитной индукции B. Силы Лоренца F₁(m) и F₂(m), действующие на каждый из зарядов Q₁ и Q₂, не совпадают по направлению и, следовательно, не могут удовлетворять закону действия и противодействия. Из рисунка очевидно, что результирующая сила действия первого заряда на второй («действие») НЕ равна результирующей силе второго заряда на первый («противодействие»), т. е. третий закон Ньютона не выполняется.

Заметим, что при   силы магнитного происхождения много меньше электрических. Поскольку отклонение от закона равенства действия и противодействия обусловлено магнитными силами, то это отношение при не очень больших скоростях несущественно и им обычно можно пренебречь.