Почему нет. 3. Динамика материальной точки

• Название: 3. Динамика материальной точки
• Анкор: Почему нет
• Дата: 11.11.2020
• Размер: 1.89 Mb.
• Имя файла: 02_Dinamika_materialnoi_774_tochki.docx
• Тип: Закон; #149643
• страница: 2 из 5

3.3. Механические силы

В этом разделе мы приведем примеры сил, действующих в механических системах. Это сила тяжести и вес тела, силы упругости и трения. Происхождение силы тяжести связано с одним из фундаментальных взаимодействий — гравитационным. (С этим взаимодействием мы познакомимся подробнее при изучении закона всемирного тяготения.) Другое фундаментальное взаимодействие — электромагнитное, то есть взаимодействие между электрическими зарядами и токами, лежит в основе сил, связанных с деформацией тел. Это, прежде всего силы упругости, а также силы трения, возникающие за счет деформации при соприкосновении шероховатых поверхностей. При деформации нарушается равновесное распределение зарядов внутри атомов, молекул или ионов, из которых состоят тела, что приводит к изменению действующих между ними сил.

Сила тяжести и вес. Ещё Галилей понял, что если не учитывать силу сопротивления воздуха, действующую на движущееся в нём тело, то все тела будут падать на Землю с одним и тем же ускорением  . Силу, «обеспечивающую» это ускорение, принято называть силой тяжести.

В системе отсчета, связанной с Землей, на всякое тело массой m действует сила тяжести



До тех пор, пока не оговорено иное, мы будет считать силу тяжести совпадающей с силой тяготения (гравитационного притяжения тела к Земле). Строго говоря, сила тяжести есть равнодействующая силы гравитационного взаимодействия тела с Землей и центробежной силы инерции, действующей на тело в любой вращающейся системе отсчета, в частности связанной с Землей. Но поскольку центробежные силы значительно меньше гравитационных, во многих задачах (не во всех) их можно не учитывать.

Дополнительная информация

http://kvant.mirror1.mccme.ru/1970/03/razmyshleniya_po_povodu_pritya.html — Журнал «Квант» — о силе притяжения тела Землей на полюсе и на экваторе (В. Левантовский);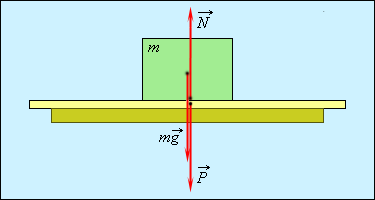



Рис. 3.15. Силы,действующие на неподвижное тело

Сила, с которой тело действует на подвес или опору, называется весом тела.

Видео 3.5. Вес тела на примере маятника Максвелла, подвешенного к коромыслу весов.

Когда тело покоится, то сила тяжести уравновешивается реакцией опоры или подвеса  , то есть

По третьему закону Ньютона вес тела   равен



Если же тело вместе с опорой или подвесом движется с ускорением, то вес тела не равен силе тяжести.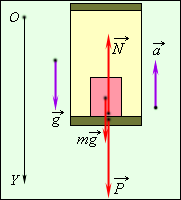



Рис. 3.16. Силы,действующие на тело, двужущееся ускоренно

Попутно напомним, что, по определению, вертикальным (вниз) направлением называется направление вектора свободного падения  . Соответственно, любое направление перпендикулярное   является горизонтальным.

Пусть подвес в виде укрепленной на раме пружины движется вместе с лифтом с ускорением а (рис. 3.17).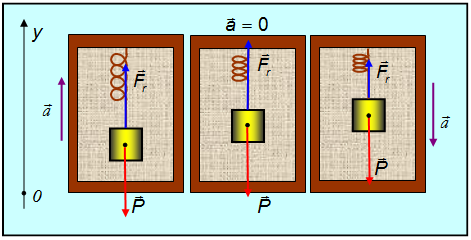



Рис. 3.17. Зависимость веса движущегося тела от ускорения опоры

Тогда уравнение движения тела будет иметь вид



где   — реакция подвеса, то есть сила, с которой пружина действует на тело. По третьему закону Ньютона тело действует на пружину с силой, равной —  , которая по определению представляет собой вес тела  . Заменив в уравнении движения реакцию опоры   силой —  , а силу тяжести   — произведением mg, получим:



Спроецируем полученное соотношение на вертикальную ось у,направленную вертикально вниз:



Отсюда вытекает, что по модулю вес   может быть как больше, так и меньше, чем сила тяжести   (см. рис. 6). При свободном падении рамы с подвесом



и сила  , с которой тело действует на подвес, равна нулю: наступает состояние невесомости. «Исчезновение» веса тела, то есть силы давления на опору, не означает исчезновения инерционных свойств тела (его массы).

В фантастической повести А.Р. Беляева «Звезда КЭЦ» описывается первое пребывание героя в состоянии невесомости. Он оттолкнулся и летит вдоль коридора космической станции:

« — Хватайтесь за ремешок! — крикнул Крамер. Эти ремешки, вроде ручек портпледа, были всюду: на стенах, на полу, на потолке. Я ухватился за ручку, ожидая, что меня рванет при остановке, но в тот же миг с удивлением почувствовал, что в руке не ощущается напряжения».

В этом описании содержится, конечно, грубая физическая ошибка: исчезновение веса героя вовсе не означает исчезновения его импульса mv. Для изменения импульса (остановки) нужна сила, так что космонавта должно было «рвануть» точно так же, как и на Земле.

Сила упругости. При деформации тела возникают силы упругости, препятствующие этой деформации. При небольших деформациях возникающие силы пропорциональны величине деформации. Если пружина в нормальном (ненагруженном) состоянии имеет длину   и мы деформируем ее (растягиваем или сжимаем) ее до длины  , то на нашу руку действует сила упругости



Коэффициент   называется коэффициентом жесткости пружины, знак «минус» указывает, что сила упругости препятствует деформации пружины. Приведенное уравнение описывает простейший случай закона Гука.

Видео 3.6. Линейные упругие деформации и закон Гука.

Возникновение упругой силы в процессе колебаний тела на пружине показано на рис. 3.18.

Дополнительная информация

http://www.plib.ru/library/book/17005.html – Стрелков С.П. Механика Изд. Наука 1971 г. – стр. 54 курсив: неупругая деформация;

http://kvant.mirror1.mccme.ru/1973/10/mehanicheskie_svojstva_kristal.html – Журнал «Квант» – о вычислении модуля упругости кристаллических твердых тел, энергии связи и других физических величин (Г.Б. Куперман, Е.Д. Щукин).

Рис. 3.18. Возникновение упругой силы в процессе колебаний тела на пружине

Пример. Каков эффективный коэффициент жесткости   для пружины, составленной из двух других пружин с коэффициентами жесткости   и   , если пружины соединены: а) последовательно (рис. 3.19), б) параллельно (рис. 3.20).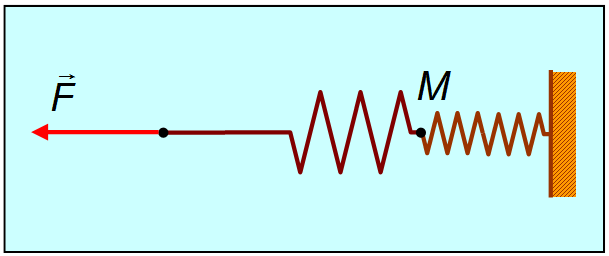



Рис. 3.19. Последовательное соединение пружин



Рис. 3.20. Параллельное соединение пружин

Решение. Если растягивать последовательно соединенные пружины, то возникающие в каждой из них упругие силы одинаковы и равны растягивающей силе   (см. рис. 7): точка соединения   находится в равновесии. Следовательно, удлинения пружин равны соответственно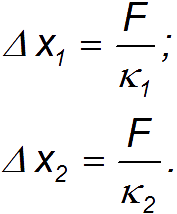



Полное удлинение составной пружины равно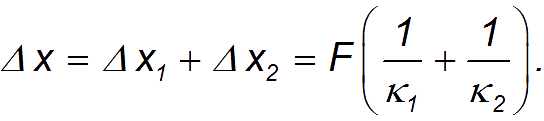



Эффективная жесткость последовательно соединенных пружин определяется из соотношения: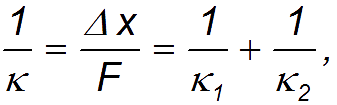



откуда



При растягивании параллельно соединенных пружин одинаковы их удлинения  , так что в каждой из них возникает своя упругая сила: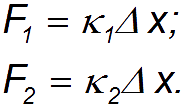



В состоянии покоя сумма этих сил равна растягивающей силе (см. рис. 3.20):



так что коэффициент жесткости параллельно соединенных пружин равен



В ряде задач, когда коэффициент жесткости велик, пренебрегают величиной деформации, но не ее последствиями возникающими силами упругости. Это тоже пример физической абстракции, модели.

Сила трения. При соприкосновении чистых — свободных от жидкой смазки — поверхностей твердых тел между ними возникают силы, называемые силами сухого трения. Их характерная черта: эти силы не обращаются в нуль даже при отсутствии относительного движения соприкасающихся тел.

Трение, которое может существовать между телами, не движущимися друг относительно друга, называется трением покоя.

Имеет место следующее утверждение относительно силы трения покоя:

Сила трения покоя всегда равна по величине и противоположна по направлению внешней силе, которая в отсутствие трения должна была бы вызвать относительное скольжение тел.

Однако сила трения покоя не может превосходить некоторой максимальной величины  . Пока внешняя сила меньше  , относительное скольжение тел не возникает, так как сила трения покоя «автоматически» принимает значение, компенсирующее действие внешней силы.

Видео 3.7. Сила трения покоя и сила трения скольжения:натюрморт с шампанским.

Силы сухого трения между объектами, движущимися друг относительно друга, называются силами трения скольжения.

Они довольно сложным образом зависят от скорости относительного движения, но для широкого класса явлений и соприкасающихся пар материалов их можно считать постоянными и равными максимальному значению силы трения покоя. Они направлены так, чтобы препятствовать относительному проскальзыванию соприкасающихся тел.

Для максимального значения силы трения покоя экспериментально установлено соотношение — закон Амонтона-Кулона:

Максимальная сила трения покоя пропорциональна силе нормального давления, прижимающего соприкасающиеся тела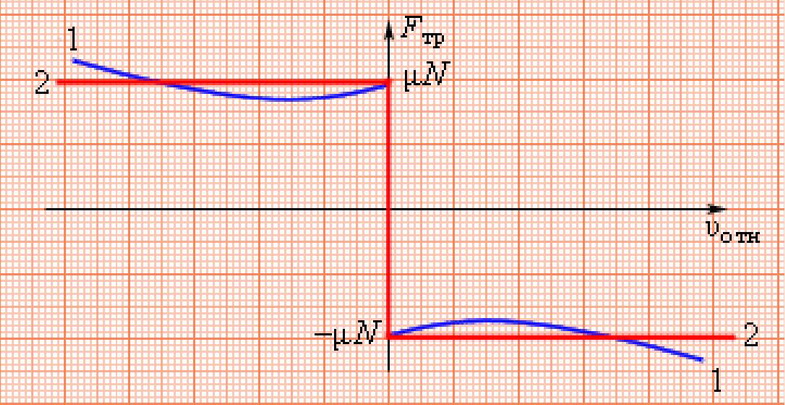





Рис. 3.21. Зависимость силы трения от относительной скорости тел

где   — коэффициент трения покоя, зависящий от свойств соприкасающихся поверхностей. Характерные значения   приведены в таблице.

Таблица

Коэффициент трения покоя для некоторых пар соприкасающихся материалов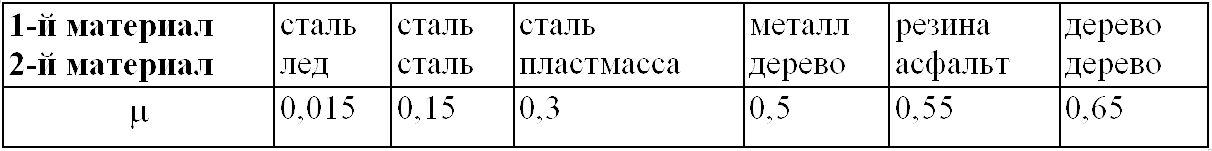



Следует иметь в виду, что коэффициент трения покоя сильно зависит не только от материалов соприкасающихся тел, но и от состояния (обработки) их поверхностей,а также от присутствия посторонних веществ, например, ржавчины на поверхности стальных деталей.

При контакте твердых тел между ними действуют не только силы сухого трения (покоя или скольжения). Из-за деформации тел могут возникать также силы трения качения. Они гораздо меньше сил трения покоя, и ими обычно пренебрегают.

Следующий пример демонстрирует случай, когда сила реакции опоры не параллельна силе тяжести. Пусть тело массой  скользит по наклонной плоскости, которая составляет угол   с горизонтом (рис. 3.22).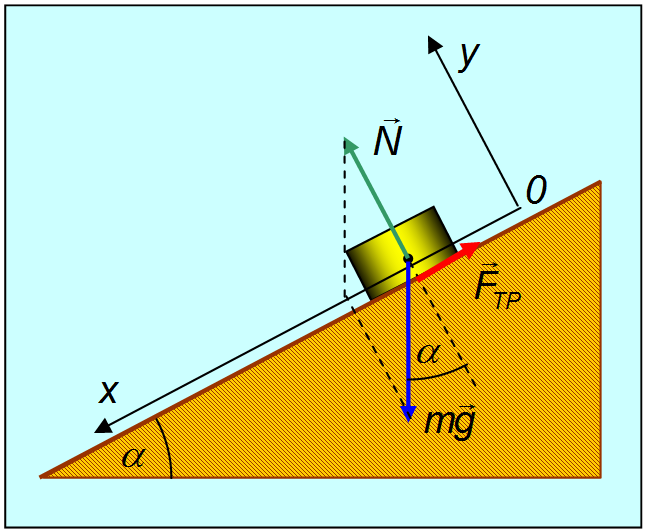



Рис. 3.22. Движение тела по наклонной плоскости

Для того чтобы составить уравнение движения, необходимо установить, какие силы действуют на рассматриваемое тело. При этом необходимо вначале выяснить, действие каких других тел на данное тело следует принять во внимание. Для тела, скользящего по наклонной плоскости, существенно воздействие со стороны Земли (оно характеризуется силой тяжести  ) и воздействие со стороны плоскости (оно характеризуется силой реакции опоры  , где   — нормальная составляющая силы реакции (сила нормального давления), а   — тангенциальная составляющая силы реакции, то есть сила трения). Соответственно, уравнение второго закона Ньютона или уравнение движения имеет вид:



Чтобы найти ускорение тела, необходимо перейти от векторов к их проекциям на соответствующим образом выбранные направления. (Обычно целесообразно в качестве одной из координатных осей выбрать ось вдоль направления движения). Спроецируем векторы, входящие в уравнение, на направления   и   (см. рис. 3.22):



(3.2.13)



(3.2.14)

Предполагая, что тело скользит вниз, вместо   подставим в первое уравнение силу трения скольжения



со значением N, следующим из второго уравнения, то есть:



(3.2.15)

Тогда из первого уравнения, после деления его на массу, для ускорения с которым тело скользит вниз, получаем:



Решим задачу в такой постановке: тело положили на наклонную плоскость и без толчка отпустили, то есть начальная скорость тела равна нулю. Если потребуется определение зависимости координаты x тела от времени t, можно положить, что её начальное значение также равным нулю.

Строго говоря, заранее неизвестно начнет тело скользить вниз или нет. Предположим, что тело остается в покое, найдем из уравнений движения значение силы трения покоя и получим условие сохранения состояния покоя из требования, что сила трения покоя не может превышать своё максимальное значение равное силе трения скольжения. Это общий прием, который приводит к результату — неравенству, при выполнении которого, сохраняется состояние покоя — не только в данном простейшем случае, но и в значительно более сложных ситуациях.

Если тело покоится, то

(3.2.16)

и фигурирующая в (3.2.13) сила трения есть сила трения покоя



(3.2.17)

Подставляя (3.2.16) и (3.2.17) в (3.2.13) для силы трения покоя получаем



(3.2.18)

Но, сила трения покоя не может превышать своё максимальное значение, равное силе трения скольжения. Потребовав, чтобы (3.2.18) не превышало (3.2.15), после сокращений получаем условие сохранения состояния покоя

(3.2.19)

При выполнении неравенства (угол мал, коэффициент трения большой), если тело не просто поставить на наклонную плоскость, а и толкнуть вверх, то тело начнет скользить замедляясь вверх, остановится и останется стоять.

При выполнении противоположного неравенства (большой угол, малый коэффициент трения)

тело будет, замедляясь скользить вверх, остановится и, «не удержавшись», заскользит вниз.

Сухое трение возникает при соприкосновении прижатых друг к другу тел в результате их относительного перемещения. Поверхности реальных тел не являются гладкими, на них имеются шероховатости (рис. 3.23). Поэтому касание тел происходит не по всей площади видимого соприкосновения, а в отдельных областях, расположенных на выступах поверхностей. При скольжении области соприкосновения разрушаются и возникают вновь. Важными последствиями трения скольжения на практике являются нагревание и износ трущихся поверхностей.



Рис. 3.23. Механизм возникновения сухого трения

Дополнительная информация

http://www.plib.ru/library/book/17005.html – Стрелков С.П. Механика Изд. Наука 1971 г. – стр. 145–149 (§ 42): сухое трение скольжения, закон Кулона, описано автомобильное сцепление;

http://vivovoco.rsl.ru/quantum/2002.01/SCHL_102.PDF — Приложение к журналу «Квант» – сухое трение (И. Слободецкий);

http://www.plib.ru/library/book/17005.html – Стрелков С.П. Механика Изд. Наука 1971 г. – стр. 261–263 (§ 75): явление заноса автомобиля при торможении на скользкой дороге;

http://www.plib.ru/library/book/17833.html – Хайкин С.Э. Физические основы механики, Наука, 1971 г.— стр. 202–205 (§ 52): при обсуждении сил сухого трения анализируется явление застоя и заноса автомобиля при торможении.

Сила сопротивления среды. При движении тела в жидкой или газообразной среде на него действует сила сопротивления среды, зависящая от скорости тела. При малых скоростях движения сила сопротивления пропорциональна скорости



При увеличении скорости тела сила сопротивления зависит от скорости по квадратичному закону



В обоих случаях сила сопротивления направлена против вектора скорости тела.

Зависимость силы от скорости тела приводит к существованию установившейся скорости движения, когда сила сопротивления достигает величины движущей силы.

Пример. Рассмотрим медленное движение тела под действием постоянной силы   = const в жидкой среде. В проекциях на направление силы второй закон Ньютона для тела имеет вид



Пусть тело начинает двигаться без начальной скорости



Интегрируя уравнение второго закона Ньютона, получим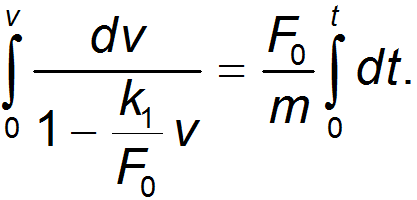



или



откуда зависимость скорости тела от времени принимает вид:



На рис. 3.24 представлена графически зависимость скорости тела от времени.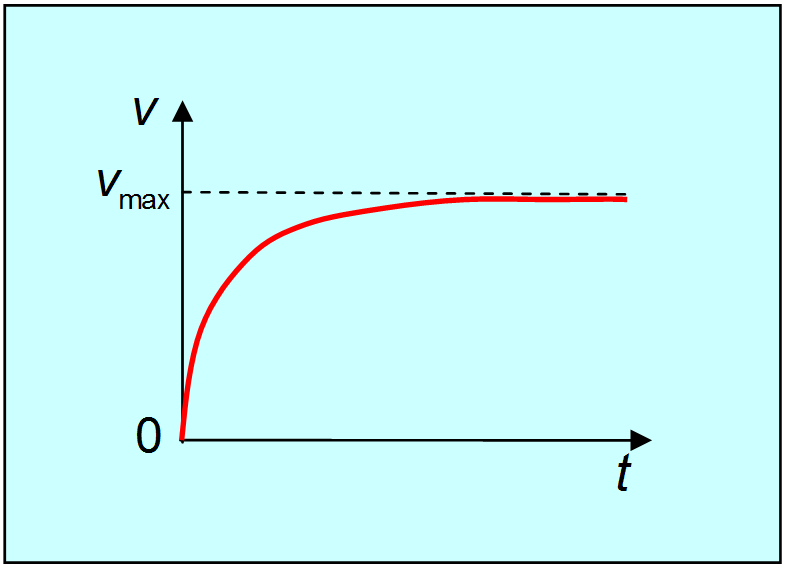



Рис. 3.24. Скорость движения тела в вязкой среде

Видно, что скорость тела с течением времени стремится к предельному значению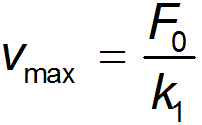



— скорости установившегося движения.