Почему нет. 3. Динамика материальной точки
 Скачать 1.89 Mb.
|
3.5. Центр массСнова рассмотрим ту же систему материальных точек. Построим радиус-вектор по следующему правилу: 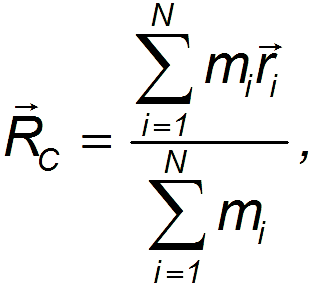 где — радиус-вектор — той материальной точки системы, а — ее масса. Радиус-вектор определяет положение в пространстве центра инерции (центра масс) системы. Вовсе не обязательно, что в центре масс системы окажется какая-то материальная точка. Пример. Найдем центр масс системы, состоящей из двух маленьких шариков — материальных точек, соединенных невесомым стержнем (рис. 3.29). Такая система тел называется гантелей. 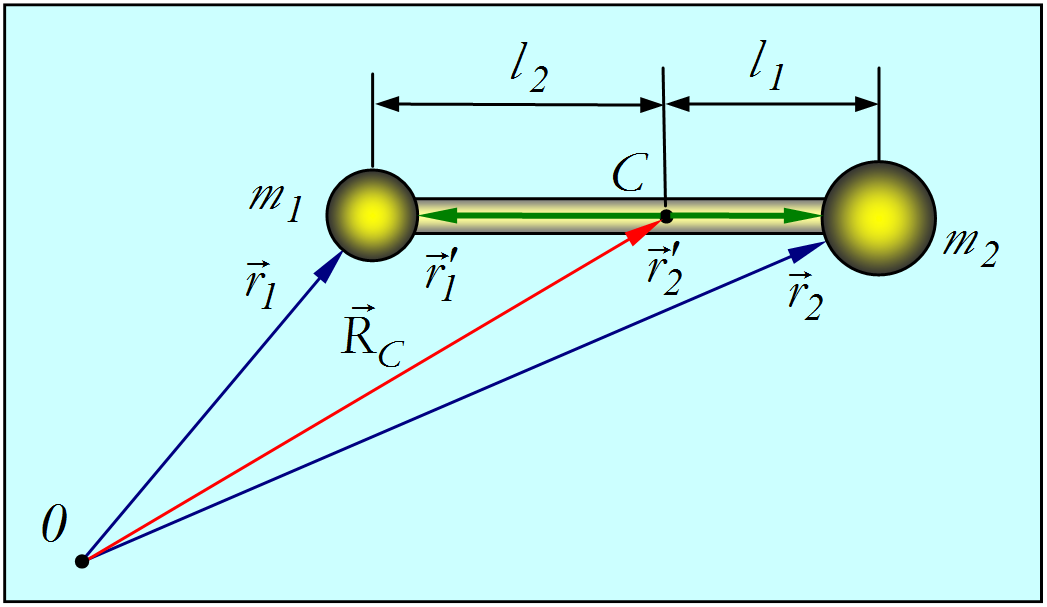 Рис. 3.29. Центр масс гантели Из рис. видно, что  и  Подставляя в эти равенства выражение для радиус-вектора центра масс  получим  и  Отсюда следует, что центр масс лежит на прямой, проходящей через центры шаров. Расстояния l1 и l2 между шарами и центром масс равны соответственно   Центр масс ближе к тому шарику, масса которого больше, что видно из отношения:  Определим, с какой скоростью движется центр инерции системы. Дифференцируем по времени обе части: 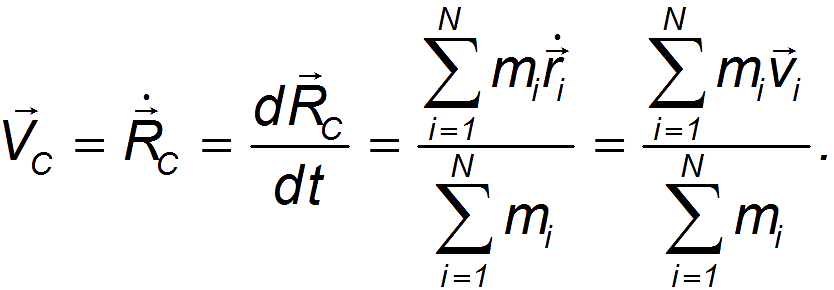 В числителе полученного выражения в правой части стоит сумма импульсов всех точек, то есть импульс системы. В знаменателе стоит полная масса системы  Мы получили, что скорость центра инерции связана с импульсом системы и ее полной массой таким же соотношением, какое справедливо для материальной точки:  Видео 3.11. Движение центра масс двух одинаковых тележек, связанных пружиной. Таким образом, можно считать, что скорость VC является скоростью системы как целого. Она, разумеется, может отличаться от скоростей каждого из тел, входящих в систему. Центр масс замкнутой системы движется всегда с постоянной скоростью, поскольку импульс такой системы сохраняется. Если продифференцировать теперь выражение для импульса системы по времени и учесть, что производная импульса системы есть равнодействующая внешних сил, то получим уравнение движения центра масс системы в общем случае:  Видно, что Центр масс системы движется точно так же, как двигалась бы материальная точка с массой, равной массе всех частиц системы, под действием векторной суммы всех внешних сил, приложенных к системе. Если имеется система материальных точек, внутреннее расположение и движение которых нас не интересует, мы вправе считать ее материальной точкой с координатами радиус-вектора центра инерции и массой, равной сумме масс материальных точек системы. Если связать с центром масс замкнутой системы материальных точек (частиц) систему отсчета (ее называют системой центра масс), то полный импульс всех частиц в такой системе окажется равным нулю. Таким образом, в системе центра масс замкнутая система частиц как целое покоится, и существует только движение частиц относительно центра масс. Поэтому ясно выявляются свойства внутренних процессов, протекающих в замкнутой системе. В случае, когда системой является тело с непрерывным распределением масс, определение центра масс остается по существу тем же. Окружаем произвольную точку в нашем теле небольшим объемом . Масса, заключенная в этом объеме, равна 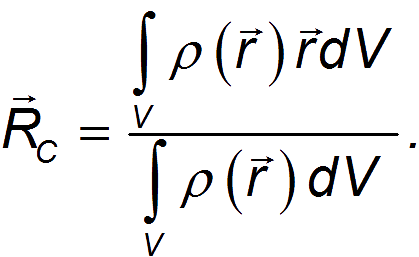 , где — плотность вещества тела, которая может и не быть постоянной по его объему. Сумма по всем таким элементарным массам заменяется теперь на интеграл по всему объему тела, так что для положения центра масс тела получается выражение Если вещество тела однородно, плотность его постоянна, и ее можно вынести из-под знака интеграла, так что она сократится в числителе и знаменателе. Тогда выражение для радиус-вектора центра масс тела принимает вид  где — объем тела. И в случае непрерывного распределения масс справедливо утверждение, что Центр масс твердого тела движется так, как двигалась бы материальная точка с массой, равной массе тела, под действием векторной суммы всех внешних сил,приложенных к телу. Пример. Если снаряд взрывается в некоторой точке своей параболической траектории, то осколки летят по самым различным траекториям, но его центр масс продолжает движение по параболе. 3.6. Реактивное движение Рассмотрим движение тела, масса которого меняется в процессе движения, на примере движения ракеты. Принцип движения ракеты заключается в том, что продукты сгорания топлива с большой скоростью выбрасываются из ракеты, толкая ее при этом в противоположную сторону. Заметим, что при движении ракеты ее масса непрерывно изменяется, следовательно, второй закон Ньютона в рассмотренной ранее форме для описания движения ракеты неприменим. 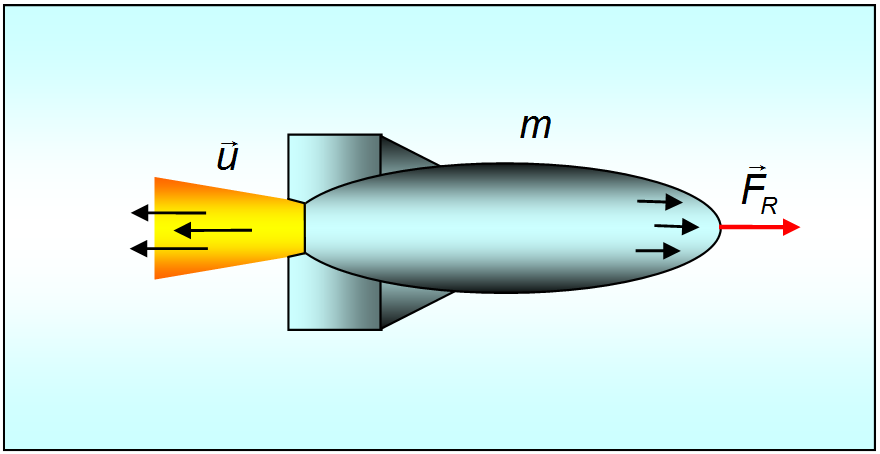 Рис. 3.30. Принцип движения ракеты Пусть — масса ракеты в момент , а — ее скорость. Импульс ракеты будет  За время масса ракеты и ее скорость получают приращения (причем < 0), так как масса ракеты убывает) и соответственно, так что к моменту времени они будут равны   Импульс ракеты станет  Кроме этого следует учесть импульс выброшенных за время газов:  где  — масса выброшенных за время газов,  — их скорость относительно Земли.Воспользуемся вторым законом Ньютона в импульсной форме. Тогда   Раскроем скобки,учитывая, что  (масса ракеты уменьшилась на массу выброшенных из сопла двигателя газов): Введем u — скорость истечения газовой струи относительно ракеты. Тогда  После преобразований и удержания членов первого порядка малости (член второго порядка малости  отброшен) получаем или  Данное уравнение по форме напоминает второй закон Ньютона, однако здесь возникает дополнительное слагаемое  называемое реактивной силой. C учетом этого уравнение движения принимает вид  Это уравнение движения тела переменной массы носит название уравнения Мещерского. Величина  называется расходом топлива. Рассмотрим движение ракеты в отсутствие внешних сил (F = 0) (рис. 3.31). Спроецируем уравнение Мещерского на направление движения ракеты : 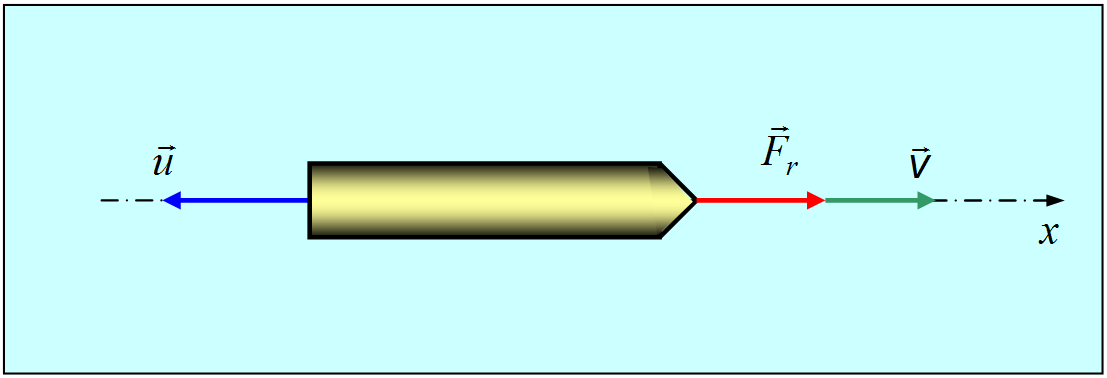  Рис 3.31. Движение ракеты в отсутствие внешних сил С учетом, что  получаем  Разделим переменные:  Обычно можно считать, что скорость истечения газов относительно ракеты постоянна. Интегрируя полученное уравнение, находим  Пусть в начальный момент = 0 мы имеем  и  Тогда  откуда находим постоянную интегрирования  Тогда формула для скорости ракеты, называемая формулой Циолковского, принимает вид  Ясно, что конечная скорость ракеты определяется скоростью истечения газовой струи, которая — в случае химического двигателя с реакцией окисления и выбросом продуктов реакции — зависит от температуры сгорания T и молярной массы газов M  .Следовательно, наиболее эффективным топливом будет водород с очень высокой температурой сгорания и малой молярной массой. Водород как топливо нашел широкое применение в космонавтике, несмотря на повышенную пожароопасность и потребность (при хранении в баках ракеты) в очень низких (криогенных) температурах. Пример. Пусть ракете необходимо сообщить первую космическую скорость = 8 км/с. Если использовать топливо со скоростью истечения = 1 км/с (порох), то отношение массы полезной нагрузки к стартовой массе ракеты будет  Если же использовать топливо с = 2 км/с (водород), то  Видно, что при одинаковой полезной нагрузке стартовая масса ракеты во втором случае будет почти в 50 раз меньше, чем в первом. |