Почему нет. 3. Динамика материальной точки
 Скачать 1.89 Mb.
|
3.4. Закон сохранения импульсаРассмотрим систему материальных точек , , …, , положения которых задаются радиус-векторами , , …, , а их импульсы равны , ,..., , соответственно (рис. 3.25). 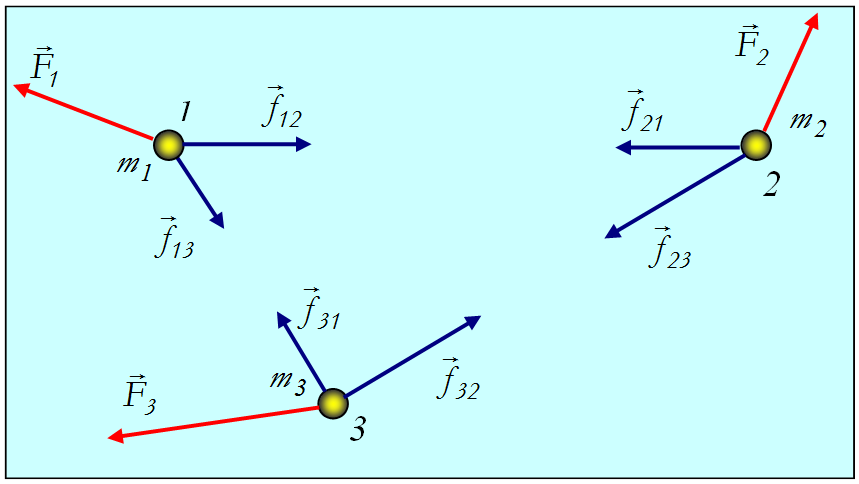 Рис. 3.25. Система взаимодействующих частиц Среди сил, действующих на эти материальные точки, будем различать внутренние силы между телами, входящими в систему, и внешние силы, действующие на систему со стороны тел, в нее не включенных. Внутренние силы будем обозначать как , где индексы показывают, что данная сила действует на тело с номером со стороны тела с номером . Кроме того, на тело с номером действует какая-то внешняя сила . Напишем уравнение второго закона Ньютона (скорость изменения импульса тела равна сумме всех действующих на тело сил) для всех материальных точек системы 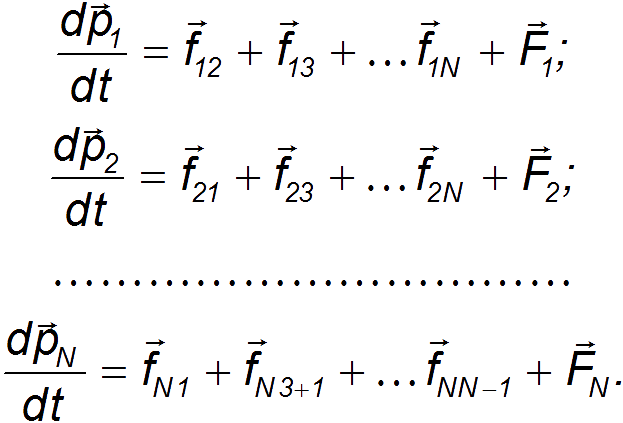 Сложим вместе эти уравнений. Сумма всех внутренних сил в правой части получится равной нулю. Действительно, она состоит из парных слагаемых типа  По третьему закону Ньютона силы взаимодействия двух материальных точек и равны по величине и противоположно направлены (действуют вдоль прямой, соединяющей эти материальные точки):  Поэтому в правой части у нас останется только сумма всех внешних сил:  Сумма  импульсов частиц, образующих механическую систему, называется импульсом системы. 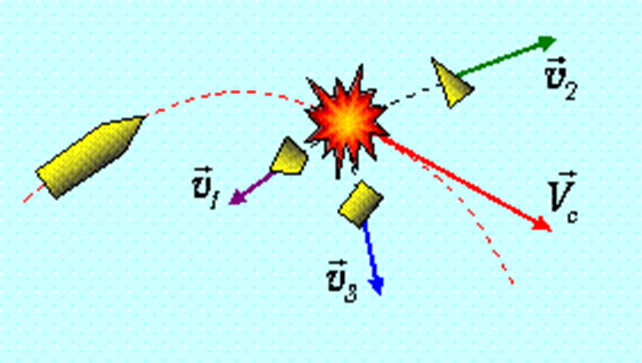 Рис. 3.26. Суммарный импульс осколков снаряда равен импульсу самого снаряда до взрыва. Импульс системы удовлетворяет уравнению  Система тел, взаимодействующих только между собой и не взаимодействующих с другими телами, называется замкнутой.  Рис. 3.27. Суммарный импульс снаряда и вылетающих частиц не меняется со временем Видео 3.8. Пояснение принципа ракетного движения: стрельба с движущейся тележки вперед, назад и вбок. Иными словами, на замкнутую систему не действуют внешние силы. При отсутствии внешних сил  откуда  Суммарный импульс  замкнутой системы постоянен сохраняется, то есть постоянен во времени.  Это утверждение, известное как закон сохранения импульса, связано с фундаментальными свойствами природы (однородностью пространства), и потому справедливо не только в классической механики, но и в физике вообще. Видео 3.9. Сохранение суммарного импульса двух тележек: тележка съезжает с подвижной тележки. Возможны ситуации, когда внешние силы не равны нулю, но равна нулю проекция их равнодействующей на некоторое направление . Тогда, как следует из (3.4.1), переписанного в виде  будет сохраняться проекция импульса системы на это же направление. Примером может служить уже рассмотренное движение тела, брошенного под углом к горизонту. На тело действует сила тяжести, направленная вертикально вниз. Ее проекция на горизонтальную ось равна нулю, и потому горизонтальная проекция импульса сохраняется, соответственно,постоянна горизонтальная проекция скорости. Применение закона сохранения импульса позволяет решить многие задачи, например, когда неизвестны точные силы, действующие в системе. 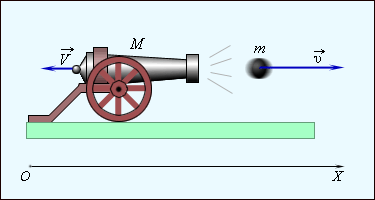 Рис. 3.28. При выстреле сохраняется проекция импульса вдоль ствола орудия Видео 3.10. Закон сохранения импульса: отдача пушки при выстреле. Стрельба привязанным к пушке снарядом. Пример. Стреляя из автомата АК-47, солдат испытывает отдачу: на него действует средняя сила Fcp, эквивалентная весу массы M = 6.5 кг. Учитывая, что масса пули m = 7 г и вылетает она с начальной скоростью 850 м/с, определить скорострельность n автомата (то есть количество пуль, выпускаемых автоматом в единицу времени). За время  выпускается  пуль. Они уносят импульс  По закону сохранения такой же импульс передается автомату. Поэтому по второму закону Ньютона средняя сила отдачи равна По условию  Отсюда находим скорострельность оружия: Естественно, при стрельбе очередями и, тем более, одиночными выстрелами число выстрелов в минуту будет меньшим. |