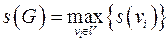|
логика. 3. Множество совокупность объектов, обладающих определенным свойством, объединенных в единое целое. Объекты, составляющие множество, называются элементами множества

1.Математическая логика - является наукой о законах математического мышления. Предметом математической логики являются математические теории в целом, которые изучаются с помощью математических языков. При этом в первую очередь интересуются вопросами непротиворечивости математических теорий, их развязности и полноты. Сфера применения математической логики очень широка. С каждым годом растет глубокое проникновение идей и методов математической логики в информатику, вычислительную математику, лингвистику, философию.
3. Множество - совокупность объектов, обладающих определенным свойством, объединенных в единое целое.Объекты, составляющие множество, называются элементами множества.
Виды множеств: пустое, конечное, бесконечное, упорядоченное
Пустое множество - множество, не содержащее ни одного элемента. Пустое множество является частью любого множества.
Пример: Множество всех действительных корней уравнения пусто.
Конечное множество - множество, состоящее из конечного числа элементов. Основной характеристикой конечного множества является число его элементов.
Теория конечных множеств изучает правила: как, зная количество элементов некоторых множеств, вычислить количество элементов других множеств, которые составлены из первых с помощью некоторых операций.
Пример: Множество всех студентов факультета математики и информатики.
Бесконечное множество - непустое множество, не являющееся конечным.
Пример: Множество натуральных чисел является бесконечным.
Упорядоченное множество - Множество, каждому элементу которого поставлено в соответствие некоторое число (немер этого элемента) от 1 до n, где n - число элементов множества, так что различным элементам соответствуют различные числа.
Каждое конечное множество можно сделать упорядоченным, если, например, переписать все элементы в некоторый список (a, b, c, d,...), а затемпоставить в соответствие каждому элементу номер места, нк котором он стоит в списке. Возможны различные способы задания множеств.Один из них состоит в том, что дается полный список элементов, входящих в это множество.
Пример: Множество учеников данного класса определяется их списком в классном журнале, множество всех стран на земном шаре - их списком в классном журнале, множество всех костей в человеческом теле - их списком в учебнике анатомии.
Существуют два основных способа задания множеств: перечисление и описание его элементов. Перечисление состоит в получении полного списка элементов множества, а описание заключается в задании такого свойства, которым элементы данного множества обладают, а все остальные нет.
4. Пересечением двух множеств называют множество, состоящее из всех общих элементов этих множеств.
Пример:
Возьмем числа 12 и 18. Найдем их делители, обозначив все множество этих делителей соответственно буквами А и B:
А = {1, 2, 3, 4, 6, 12},
B = {1, 2, 3, 6, 9, 18}.
Мы видим, что у чисел 12 и 18 есть общие делители: 1, 2, 3, 6. Обозначим их буквой C:
C = {1, 2, 3, 6}.
Множество C и является пересечением множеств А и B. Пишут это так:
А ∩B =C.
А ∩B={1, 2, 3, 6}.
Если два множества не имеют общих элементов, то пересечением этих множеств является пустоемножество.
Пустое множество обозначают знаком Ø, а используют такую запись:
X ∩Y = Ø.
Объединение двух множеств – это множество, состоящее из всех элементов этих множеств.
Для примера вернемся к числам 12 и 18 и множеству их элементов A и B. Выпишем сначала элементы множества А, затем добавим к ним те элементы множества B, которых нет во множестве А. Мы получим множество элементов, которым обладают А и B в совокупности. Обозначим его буквой D:
D = {1, 2, 3, 4, 6, 12, 9, 18}.
Множество D и является объединением множеств A и B. Пишется это так:
D =AUB.
AUB={1, 2, 3, 4, 6, 12, 9, 18}.
5.Декартовым произведением множествA и B называется такое результирующее множество пар вида (x,y), построенных таким образом, что первый элемент из множества A, а второй элемент пары — из множества B. Общепринятое обозначение:
A×B={(x,y)|x∈A,y∈B}
Произведения трёх и более множеств можно построить следующим образом:
A×B×C={(x,y,z)|x∈A,y∈B,z∈C}
Примеры
1.Положим A={1,2},B={3,4}. Тогда результат декартова произведения можно записать так: A×B={(1,3),(1,4),(2,3),(2,4)}, а B×A={(3,1),(3,2),(4,1),(4,2)}
2.Если в предыдущем примере положить B=A, очевидно, что A×B=B×A={(1,3),(1,4),(2,3),(2,4)}
3.Возьмём A={x∈R|0≤x≤5},B={x∈R|5≤x≤10}. Тогда A×B={(x,y)∈R^2|0≤x≤5∧5≤x≤10}
6. Разностью множеств A и B называется множество элементов, принадлежащих A и не принадлежащих B. Обозначают A\B и читают "разность A и B".
Пример 1. Пусть A есть отрезок [1, 3], B - отрезок [2, 4]; тогда объединением 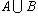 будет отрезок [1, 4], пересечением будет отрезок [1, 4], пересечением 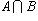 - отрезок [2, 3], разностью A\B- полуинтервал [1, 2), B\A - полуинтервал (3, 4]. - отрезок [2, 3], разностью A\B- полуинтервал [1, 2), B\A - полуинтервал (3, 4].
Пример 2. Пусть A есть множество прямоугольников, B - множество всех ромбов на плоскости. Тогда 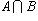 есть множество всех квадратов, A\B - множество прямоугольников с неравными сторонами, B\A - множество всех ромбов с неравными углами. есть множество всех квадратов, A\B - множество прямоугольников с неравными сторонами, B\A - множество всех ромбов с неравными углами.
7. Пересечение множеств является бинарной операцией на произвольном булеане ;
Операция пересечения множеств коммутативна:
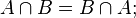
Операция пересечения множеств транзитивна:
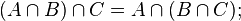
Универсальное множество является нейтральным элементом операции пересечения множеств:
Таким образом булеан вместе с операцией пересечения множеств является абелевой группой;
Операция пересечения множеств идемпотентна:
Если — пустое множество, то
8.Объединение множеств является бинарной операцией на произвольном булеане
Операция объединения множеств коммутативна:
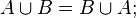
Операция объединения множеств транзитивна:
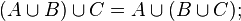
Пустое множество является нейтральным элементом операции объединения множеств:
Таким образом булеан вместе с операцией объединения множеств является моноидом;
Операция пересечения множеств идемпотентна:
9. Виды отношений 1.Бинарное отношение (двучленное отношение). Бина́рное отноше́ние в математике — двухместное отношение между любыми двумя множествами и , то есть всякое подмножество декартова произведения этих множеств: 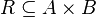 [1]. Бинарное отношение на множестве — любое подмножество [1]. Бинарное отношение на множестве — любое подмножество 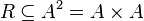 , такие бинарные отношения наиболее часто используются в математике, в частности, таковы равенство, неравенство, эквивалентность, отношение порядка. , такие бинарные отношения наиболее часто используются в математике, в частности, таковы равенство, неравенство, эквивалентность, отношение порядка.
2. Тернарное отношение — то же, что трёхместное отношение (трёхчленное отношение).
3.Кватернарное отношение — то же, что четырёхместное отношение (четырёхчленное отношение)
10. Рефлексивное отношение в математике — бинарное отношение на множестве , при котором всякий элемент этого множества находится в отношении с самим собой.
Формально, отношение рефлексивно, если 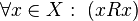 . .
Свойство рефлексивности при заданных отношениях матрицей характеризуется тем, что все диагональные элементы матрицы равняются 1; при заданных отношениях графом каждый элемент х имеет петлю — дугу (х, х).
Бинарное отношение на множестве является рефлексивным тогда и только тогда, когда его подмножеством является тождественное отношение на множестве (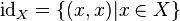 ), то есть . ), то есть .
Если это условие не выполнено ни для какого элемента множества , то отношение называется антирефлексивным (или иррефлексивным).
Если антирефлексивное отношение задано матрицей, то все диагональные элементы являются нулевыми. При задании такого отношения графом каждая вершина не имеет петли — нет дуг вида (х, х).
Формально антирефлексивность отношения определяется как: 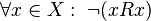 . .
Если условие рефлексивности выполнено не для всех элементов множества , говорят, что отношение нерефлексивно.
Примеры рефлексивных отношений
отношения эквивалентности:
отношение равенства
отношение сравнимости по модулю
отношение параллельности прямых и плоскостей
отношение подобия геометрических фигур;
отношения нестрогого порядка:
отношение нестрогого неравенства
отношение нестрогого подмножества
отношение делимости
Примеры антирефлексивных отношений
отношение неравенства
отношения строгого порядка:
отношение строгого неравенства
отношение строгого подмножества
отношение перпендикулярности прямых (или ортогональности ненулевых векторов) в евклидовом пространстве.
11. Транзитивное отношение в математике - это такое отношение, при котором если один элемент соотносится с вторым, а второй с третьим, то и первый элемент соотносится с третьим.
В математике бинарное отношение на множестве называется транзитивным, если для любых трёх элементов множества выполнение отношений и влечёт выполнение отношения . Формально, отношение транзитивно, если 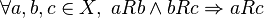 . .
Свойства
Если бинарное отношение транзитивно, то его обратное также транзитивно.
Пересечение двух транзитивных отношений также транзитивно. Это, вообще говоря, неверно дляобъединения.
Примеры
Равенство: и , значит (на самом деле, отношение равенства вместе с отношением эквивалентности и параллельности прямых обладает более сильным свойством также ещё и «равенства третьему» по причине своей симметричности)
Отношение порядка: b" ALIGN=BOTTOM WIDTH=46 HEIGHT=14 BORDER=0> и c" ALIGN=BOTTOM WIDTH=44 HEIGHT=14 BORDER=0>, значит c" ALIGN=BOTTOM WIDTH=46 HEIGHT=12 BORDER=0> или нестрогого порядка: и , значит
Параллельностьпрямых: и , значит (см. примечание к «равенству чисел»)
Импликация: и , значит
Эквивалентность: и , значит (см. примечание к «равенству чисел»)
Включение подмножества: если b является подмножеством a, и в свою очередь c является подмножеством b, тогда c является подмножеством a
Делимость: если a делится на b, и b делится на c, тогда a делится на c.
Отношение следования вершин ориентированного графа: если вершина достижима из вершины , а вершина , в свою очередь, — из , то достижима из .
12. Отношение эквивалентности () на множестве — это бинарное отношение, для которого выполнены следующие условия:
1.Рефлексивность: для любого в ,
2.Симметричность: если , то ,
3.Транзитивность: если и , то .
Запись вида «» читается как « эквивалентно ».
Примеры отношений эквивалентности
Равенство («»), тривиальное отношение эквивалентности на любом множестве, в частности, вещественных чисел.
Сравнение по модулю, («а ≡ b (mod n)»).
В евклидовой геометрии
Отношение конгруэнтности («»).
Отношение подобия («»).
Отношение параллельности прямых («»).
13. ВЫСКАЗЫВАНИЕ - это повествовательное предложение, о котором можно сказать, что оно истинно или ложно.
Высказывание, которое можно разложить на части, будем называть сложным, а неразложимое далее высказывание - простым.
Сложное высказывание получается путем объединения простых высказываний связками - частицей НЕ; союзами И; ИЛИ; НЕВЕРНО, ЧТО...; ТОГДА И ТОЛЬКО ТОГДА..., КОГДА...; ЕСЛИ..., ТО... Значение истинности cложных высказываний зависит от истинности входящих в них простых высказываний и объединяющих их связок.
Например, даны четыре простых высказывания:
На улице идет дождь. (1)
На улице светит солнце. (2)
На улице пасмурная погода. (3)
На улице идет снег. (4)
Составим из них сложные высказывания:
На улице идет дождь и на улице светит солнце.
На улице светит солнце или на улице пасмурная погода.
Неверно что на улице идет дождь и на улице идет снег.
Тогда и только тогда на улице идет дождь, когда на улице пасмурная погода.
На улице не идет дождь и на улице не идет снег.
Если на улице идет дождь, то на улице светит солнце.
14. Конъюнкция
Конъюнкцией высказываний А и В называется высказывание, которое истинно, когда истинны оба данные высказывания одновременно Конъю́нкция - логическая операция, по применению максимально приближенная к союзу «и». Синонимы: логи́ческое «И», логи́ческое умноже́ние, иногда просто «И».
Конъюнкция высказываний А и В обозначается: . Читаем: «Конъюнкция высказываний А и В» или «А и В».
Название «конъюнкция» произошло от латинского слова «conjunctio», что означает «союз, связьилиединение». Определение конъюнкции высказываний А и В можно записать в следующей таблице.
a
|
b
|
|
1
|
1 1
|
1
|
1
|
0
|
0
|
0
|
1
|
0
|
0
|
0
|
0
|
Дизъюнкция
Дизъюнкцией высказываний А и В называется высказывание, которое истинно, когда истинно хотя бы одно из данных высказываний. Дизъю́нкция - логическая операция, по своему применению максимально приближённая к союзу «или»
Дизъюнкция высказываний А и В обозначается: . Читаем: «Дизъюнкция высказываний А и В» или «А или В».
Название «дизъюнкция» произошло от латинского слова «disjunctio», что означает «разделение, разобщение».
Определение дизъюнкции высказываний А и В можно записать в следующей таблице.
a
|
b
|
|
1
|
1
|
1
|
1
|
0
|
1
|
0
|
1
|
1
|
0
|
0
|
0
|
Отрицание
Отрицание - логическая операция, по своему применению максимально приближённая к союзу «не»
Отрицанием Ā некоторого высказывания А называется такое высказывание, которое истинно, когда А ложно, и ложно, когда А истинно.
Определение отрицания может быть записано с помощью так называемой таблицы истинности:
x
|
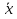
|
1
|
0
|
0
|
1
|
15. Импликация. Импликацией двух высказываний P и Q называется высказывание, истинное тогда и только тогда, когда высказывание Р истинно, а Q – ложно.
Обозначается PQ (или РQ). Высказывание Р называется посылкой импликации, а высказывание Q – следствием.
-
P |
Q
|
PQ
|
И
|
И
|
И
|
И
|
Л
|
Л
|
Л
|
И
|
И
|
Л
|
Л
|
И
|
Эквиваленция. Эквиваленцией двух высказываний P и Q называется высказывание, истинное тогда и только тогда, когда истинности высказываний совпадают.
Обозначается РQ или РQ.
-
P |
Q
|
PQ
|
И
|
И
|
И
|
И
|
Л
|
Л
|
Л
|
И
|
Л
|
Л
|
Л
|
И
|
16. Метод математической индукции
Метод математической индукции является важным способом доказательства предложений (утверждений), зависящих от натурального аргумента.
Метод математической индукции состоит в следующем:
Предложение (утверждение) P(n), зависящее от натурального числа n, справедливо для любого натурального n если:
1.P(1) является истинным предложением (утверждением);
2.P(n) остается истинным предложением (утверждением), если n увеличить на единицу, то есть P(n + 1) - истинное предложение (утверждение).
Таким образом метод математической индукции предполагает два этапа:
1.Этап проверки: проверяется, истинно ли предложение (утверждение) P(1).
2.Этап доказательства: предполагается, что предложение P(n) истинно, и доказывается истинность предложения P(n + 1) (n увеличено на единицу).
Пример: Доказать следующие равенства
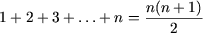
При n = 1 равенство примет вид 1=1 , следовательно, P(1) истинно
При P(n +1), 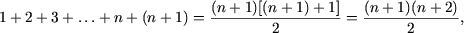
истинно. Поскольку 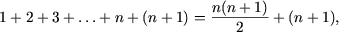
получим 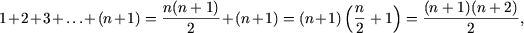
то есть, P(n + 1) - истинное утверждение.
Таким образом, согласно методу математической индукции, исходное равенство справедливо для любого натурального n.
17. Элементы комбинаторики.
Если из множества, содержащего m элементов, требуется выбрать какие-то k элементов, то возникает вопрос: сколькими способами это можно сделать и какие подмножества при этом получаются. Такие задачи называются комбинаторными, а соответствующий раздел математики – комбинаторикой.
Все формулы для подсчета числа решений в комбинаторных задачах опираются на правило произведения: если элемент X можно выбрать k способами, а элемент Y можно выбрать n способами, то пару XY можно составить kn способами.
Размещение с повторением. Из множества, содержащего m элементов, нужно выбрать k элементов, причем выбранный элемент, после того, как его взяли, вновь возвращается в исходное множество (то есть элементы в выбранном множестве могут повторяться). Пользуясь правилом произведения, получим, что каждый из k элементов может быть выбран m способами. Таким образом, общее число комбинаций равно .
Пример. Сколько различных четырехзначных чисел можно составить из цифр 2, 3, 5, 7.
Решение. Первой цифрой в числе может быть любая из четырех имеющихся. То же самое можно сказать и о последующих цифрах числа, поэтому общее число комбинаций:
Размещение без повторений. Из множества, содержащего m различных элементов, надо выбрать упорядоченное подмножество из k элементов (k m), то есть такое подмножество, в котором элементы располагаются в определенном порядке, и изменение порядка элементов изменяет подмножество. Кроме этого, элементы в выбранном подмножестве не повторяются. Требуется выяснить, сколько таких комбинаций существует. По правилу произведения получаем, что первый элемент можно выбрать m способами, второй элемент – (m-1) способом, и так далее, а элемент с номером k можно выбрать (m – k + 1) способами. Следовательно, число упорядоченных k-элементных подмножеств, взятых из множества, содержащего m элементов равно m(m-1)(m-2)…(m-k+1). Такие подмножества называются размещениями из m элементов по k элементов, а их общее число можно выразить формулой
Пример. Сколько различных четырехзначных чисел можно составить из цифр 1, 2, 3, 4, 5, 6, при условии. Что цифры в числе не повторяются?
Решение. Общее число комбинаций равно числу размещений из 6 элементов по 4: 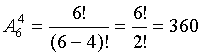
Перестановки. Пусть множество содержит m различных элементов. Рассмотрим все возможные варианты перестановок элементов этого множества. Получаемые при этом упорядоченные множества отличаются друг от друга только порядком входящих в них элементов. Такие упорядоченные множества называются перестановками. Число перестановок из m элементов равно:
Пример. Сколько различных четырехзначных чисел можно составить из цифр 2, 3, 5. 7, если цифры в числе не повторяются?
Решение. Количество чисел равно числу перестановок из четырех элементов:
Сочетания. Пусть из множества, содержащего m различных элементов, требуется выбрать подмножество, содержащее k различных элементов (k m). Получаемые при этом подмножества не упорядочены. Такие неупорядоченные подмножества называются сочетаниями. Число сочетаний из m элементов по k элементов вычисляется по формуле:
Пример. В группе 10 студентов. Сколькими способами можно выбрать из этой группы троих студентов для участия в конференции?
Решение. Число способов равно числу сочетаний из 10 элементов по 3 элемента: .
18. Полином Жегалкина — многочлен над кольцом , то есть полином с коэффициентами вида 0 и 1, где в качестве произведения берётся конъюнкция, а в качестве сложения —исключающее или. Полином был предложен в 1927 году Иваном Жегалкиным в качестве удобного средства для представления функций булевой логики. В зарубежной литературе представление в виде полинома Жегалкина обычно называется алгебраической нормальной формой (АНФ).
Теорема Жегалкина — утверждение о существовании и единственности представления всякой булевой функции в виде полинома Жегалкина.
Полином Жегалкина представляет собой сумму по модулю два произведений неинвертированных переменных, а также (если необходимо) константы 1. Формально полином Жегалкина можно представить в виде
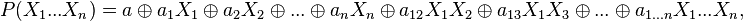
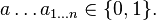
или в более формализованном виде как:
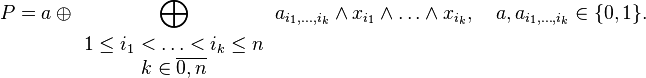
Примеры полиномов Жегалкина:
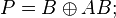
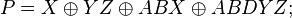
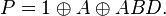
19. Конъюнкцией предикатов 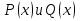 называют предикат называют предикат 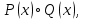 определенный на том же множестве и обращающийся в истинное высказывание при тех и только тех определенный на том же множестве и обращающийся в истинное высказывание при тех и только тех 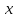 , при которых оба предиката обращаются в истинные высказывания: , при которых оба предиката обращаются в истинные высказывания:
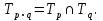
Дизъюнкцией предикатов 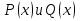 называют предикат называют предикат 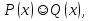 определенный на том же множестве и обращающийся в истинное высказывание при тех и только тех определенный на том же множестве и обращающийся в истинное высказывание при тех и только тех 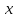 , при которых хотя бы один из этих предикатов обращается в истинное высказывание: , при которых хотя бы один из этих предикатов обращается в истинное высказывание:

Отрицанием предиката 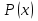 называют предикат называют предикат 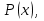 определенный на том же множестве и обращающийся в истинное высказывание при тех значения определенный на том же множестве и обращающийся в истинное высказывание при тех значения 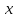 , при которых , при которых 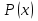 обращается в ложное высказывание, т.е. обращается в ложное высказывание, т.е.

20.Импликацией предикатов 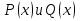 называют предикат называют предикат 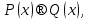 определенный на том же множестве и обращающийся в да ложное высказыванием при тех и только тех определенный на том же множестве и обращающийся в да ложное высказыванием при тех и только тех  при которых при которых 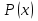 обращаются в истинные высказывания, а обращаются в истинные высказывания, а 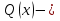 ложное. Согласно данному определению область ложности импликации предикатов находят по формуле ложное. Согласно данному определению область ложности импликации предикатов находят по формуле

А область истинности импликации предикатов по формуле
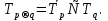
Эквиваленцией предикатов 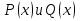 называют предикат называют предикат 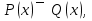
Определенный на том же множестве и обращающийся в истинное высказывание при тех и только тех  при которых при которых 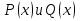 обращаются оба в истинные высказывания или оба в ложные. обращаются оба в истинные высказывания или оба в ложные.
Пользуясь данным определением, можно записать формулу для нахождения области истинности эквиваленции предикатов:
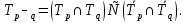
Последнюю формулу можно записать иначе:
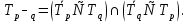
21. Формула бинома Ньютона для натуральных n имеет вид 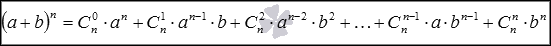 , где , где 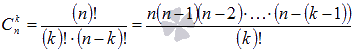 - биномиальные коэффициенты, представляющие из себя сочетания из n по k, k=0,1,2,…,n, а "!" – это знак факториала). - биномиальные коэффициенты, представляющие из себя сочетания из n по k, k=0,1,2,…,n, а "!" – это знак факториала).
К примеру, известная формула сокращенного умножения "квадрат суммы" вида 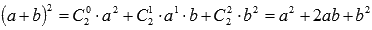 есть частный случай бинома Ньютона при n=2. есть частный случай бинома Ньютона при n=2.
Выражение, которое находится в правой части формулы бинома Ньютона, называютразложением выражения (a+b)n, а выражение 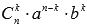 называют (k+1)-ым членом разложения, k=0,1,2,…,n. называют (k+1)-ым членом разложения, k=0,1,2,…,n.
22. Формула де-Моргана:

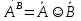
23. Теория графов – это раздел дискретной математики, исследующий свойства конечных множеств с заданными отношениями между их элементами.
Граф – это конечное множество Х, состоящее из n элементов 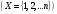 называемых вершинами графа, и подмножество V декартова произведения называемых вершинами графа, и подмножество V декартова произведения 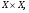 называемое множеством дуг. называемое множеством дуг.
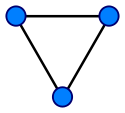
Граф, или неориентированный граф — это упорядоченная пара 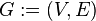 , где — это непустое множество вершин или узлов, а — множество пар (в случае неориентированного графа — неупорядоченных) вершин, называемых рёбрами. , где — это непустое множество вершин или узлов, а — множество пар (в случае неориентированного графа — неупорядоченных) вершин, называемых рёбрами.
(а значит и, , иначе оно было бы мультимножеством) обычно считаются конечными множествами. Многие результаты, полученные для конечных графов, неверны (или каким-либо образом отличаются) для бесконечных графов, поскольку не все утверждения, имеющие место для конечных совокупностей, выполняются в случае бесконечных множеств.
Вершины и рёбра графа называются также элементами графа, число вершин в графе — порядком, число рёбер — размером графа.
Вершины и называются концевыми вершинами (или просто концами) ребра . Ребро, в свою очередь, соединяет эти вершины. Две концевые вершины одного и того же ребра называются соседними.
Два ребра называются смежными, если они имеют общую концевую вершину.
Два ребра называются кратными, если множества их концевых вершин совпадают.
Ребро называется петлёй, если его концы совпадают, то есть .
Степенью вершины называют количество инцидентных ей рёбер (при этом петли считают дважды).
Вершина называется изолированной, если она не является концом ни для одного ребра; висячей (или листом), если она является концом ровно одного ребра.
Графы делятся на два типа,обычные и сложные
Ориентированный граф
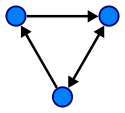
Ориентированный граф (сокращённо орграф) — это упорядоченная пара 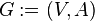 , где — непустое множество вершин или узлов, и — множество (упорядоченных) пар различных вершин, называемых дугами или ориентированными рёбрами. , где — непустое множество вершин или узлов, и — множество (упорядоченных) пар различных вершин, называемых дугами или ориентированными рёбрами.
Дуга — это упорядоченная пара вершин , где вершину называют началом, а — концом дуги. Можно сказать, что дуга ведёт от вершины к вершине .
Смешанный граф
Смешанный граф — это граф, в котором некоторые рёбра могут быть ориентированными, а некоторые — неориентированными. Записывается упорядоченной тройкой 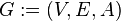 , где , и определены так же, как выше. , где , и определены так же, как выше.
Ориентированный и неориентированный графы являются частными случаями смешанного.
Изоморфные графы
Граф называется изоморфным графу , если существует биекция из множества вершин графа в множество вершин графа , обладающая следующим свойством: если в графе есть ребро из вершины в вершину , то в графе должно быть ребро из вершины в вершину и наоборот — если в графе есть ребро из вершины в вершину , то в графе должно быть ребро из вершины в вершину . В случае ориентированного графа эта биекция также должна сохранять ориентацию ребра. В случае взвешенного графа биекция также должна сохранять вес ребра.
24. Степень вершины (англ. degree, также валентность, англ. valency) в теории графов — количество рёбер графа , инцидентных вершине . При подсчёте степени ребро-петля учитывается дважды. Степень вершины обозначается как (в западных источниках — ). Максимальная и минимальная степень вершин графа G обозначаются соответственно Δ(G) и δ(G). На рис. 1 максимальная степень равна 5, минимальная — 0. В регулярном графе степени всех вершин одинаковы, поэтому в данном случае можно говорить о степени графа.
Степенью графа называется величина 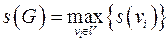
Теорема . Сумма степеней всех вершин графа равна удвоенному количеству всех ребер
25.Путемв графе от одной вершины к другой называется такая последовательность ребер, по которой можно проложить маршрут между этими вершинами. При этом никакое ребро маршрута не должно встречаться более одного раза.
Граф называется связным, если для любой пары различных вершин этого графа существует цепь, соединяющая эти вершины.
Если для графа можно указать пару различных вершин, которые не соединяются простой цепью, то граф называется несвязным.
Эйлеровы графы
Эйлеровым путем в графе называется путь, содержащий все ребра графа. Эйлеровым циклом в графе называется цикл, содержащий все ребра графа.
Связный граф 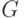 называется эйлеровым, если существует замкнутая цепь, проходящая через каждое его ребро. Такая цепь называетсяэйлеровой цепью. Отметим, что в этом определении требуется, чтобы каждое ребро проходилось только один раз. Если снять ограничение на замкнутость цепи, то граф называется полуэйлеровым, при этом каждый эйлеров граф будет полуэйлеровым. называется эйлеровым, если существует замкнутая цепь, проходящая через каждое его ребро. Такая цепь называетсяэйлеровой цепью. Отметим, что в этом определении требуется, чтобы каждое ребро проходилось только один раз. Если снять ограничение на замкнутость цепи, то граф называется полуэйлеровым, при этом каждый эйлеров граф будет полуэйлеровым.
Примеры.

Теорема 4.1. Если граф 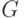 обладает эйлеровым циклом, то он является связным, а все его вершины — четными. обладает эйлеровым циклом, то он является связным, а все его вершины — четными.
Теорема 4.2. Если граф 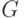 связный и все его вершины четные, то он обладает эйлеровым циклом. связный и все его вершины четные, то он обладает эйлеровым циклом.
Теорема 4.3. Если граф 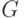 обладает эйлеровым путем с концами обладает эйлеровым путем с концами 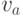 и и 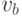 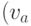 не совпадает с не совпадает с 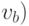 , то граф , то граф 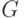 является связным, и является связным, и 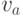 и и 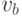 — единственные нечетные его вершины. — единственные нечетные его вершины.
Теорема 4.4. Если граф 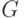 связный и связный и 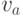 и и 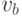 единственные нечетные вершины его, то граф единственные нечетные вершины его, то граф 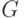 обладает эйлеровым путем с концами обладает эйлеровым путем с концами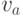 и и 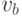 . .
Теорема 4.5. Если связный граф 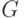 имеет имеет 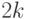 нечетных вершин, то найдется семейство из нечетных вершин, то найдется семейство из 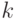 путей, которые в совокупности содержат все ребра графа в точности по одному разу. путей, которые в совокупности содержат все ребра графа в точности по одному разу.
|
|
|
 Скачать 201.25 Kb.
Скачать 201.25 Kb.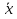
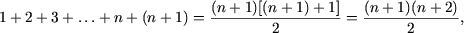
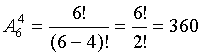
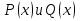 называют предикат
называют предикат 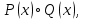 определенный на том же множестве и обращающийся в истинное высказывание при тех и только тех
определенный на том же множестве и обращающийся в истинное высказывание при тех и только тех 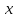 , при которых оба предиката обращаются в истинные высказывания:
, при которых оба предиката обращаются в истинные высказывания: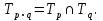
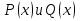 называют предикат
называют предикат 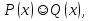 определенный на том же множестве и обращающийся в истинное высказывание при тех и только тех
определенный на том же множестве и обращающийся в истинное высказывание при тех и только тех 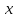 , при которых хотя бы один из этих предикатов обращается в истинное высказывание:
, при которых хотя бы один из этих предикатов обращается в истинное высказывание:
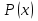 называют предикат
называют предикат 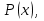 определенный на том же множестве и обращающийся в истинное высказывание при тех значения
определенный на том же множестве и обращающийся в истинное высказывание при тех значения 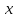 , при которых
, при которых 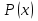 обращается в ложное высказывание, т.е.
обращается в ложное высказывание, т.е.
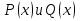 называют предикат
называют предикат 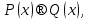 определенный на том же множестве и обращающийся в да ложное высказыванием при тех и только тех
определенный на том же множестве и обращающийся в да ложное высказыванием при тех и только тех  при которых
при которых 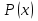 обращаются в истинные высказывания, а
обращаются в истинные высказывания, а 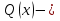 ложное. Согласно данному определению область ложности импликации предикатов находят по формуле
ложное. Согласно данному определению область ложности импликации предикатов находят по формуле
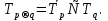
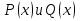 называют предикат
называют предикат 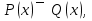
 при которых
при которых 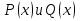 обращаются оба в истинные высказывания или оба в ложные.
обращаются оба в истинные высказывания или оба в ложные.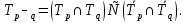
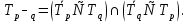
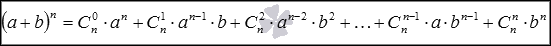 , где
, где 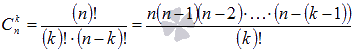 - биномиальные коэффициенты, представляющие из себя сочетания из n по k, k=0,1,2,…,n, а "!" – это знак факториала).
- биномиальные коэффициенты, представляющие из себя сочетания из n по k, k=0,1,2,…,n, а "!" – это знак факториала).
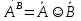
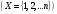 называемых вершинами графа, и подмножество V декартова произведения
называемых вершинами графа, и подмножество V декартова произведения 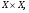 называемое множеством дуг.
называемое множеством дуг.