Итоговая контрольная работа по математике 11 класс. 3. Распределение заданий по проверяемым предметным способам действия
 Скачать 184.68 Kb.
|
|
1. Цель – выявление уровня освоения предметных образовательных результатов в соответствии с требованиями ООП и стандарта. 2. Структура итоговой работы Структура КИМ направлена на решение двух задач: формирования у всех обучающихся базовой математической подготовки, составляющей функциональную основу общего образования, и формирования математической подготовки для заданий повышенного уровня. Работа состоит из двух модулей: «Алгебра», «Геометрия». В модуль «Алгебра», входит две части, соответствующие проверке на базовом и повышенном уровнях. Модуль «Алгебра» содержит 8 заданий: в части 1 – 5 заданий; в части 2 – 3 задания. Модуль «Геометрия» содержит 3 задания. Всего в работе 11 заданий, из которых 8 заданий базового уровня, 3 задания повышенного уровня. 3. Распределение заданий по проверяемым предметным способам действия:
4. Продолжительность диагностической работы На выполнение диагностической работы по математике даётся 90 минут. 5. Критерии оценивания: Максимальный балл за работу в целом – 14. Задания, оцениваемые 1 баллом (1 часть), считаются выполненными верно, если вписан верный ответ.
ВАРИАНТ 1. Часть 1. 1. Найдите значение выражения:  2. Решите уравнение  .3. В правильной треугольной пирамиде SABC точка M – середина ребра AB, S – вершина. Известно, что BC = 3, а площадь боковой поверхности пирамиды равна 45. Найдите длину отрезка SM. 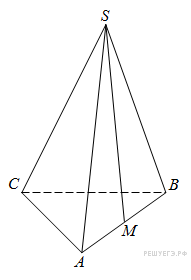 4. Объем конуса равен 16. Через середину высоты параллельно основанию конуса проведено сечение, которое является основанием меньшего конуса с той же вершиной. Найдите объем меньшего конуса. 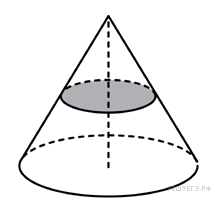 5. Найдите хорду, на которую опирается угол 120°, вписанный в окружность радиуса 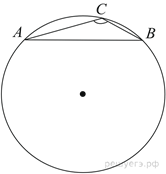  6. На рисунке изображен график производной функции f(x), определенной на интервале (−10; 2). Найдите количество точек, в которых касательная к графику функции f(x) параллельна прямой y = −2x − 11 или совпадает с ней. 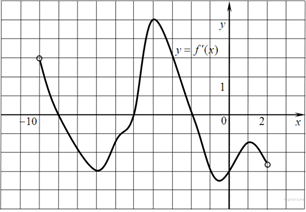  7. На рисунке изображён график функции y = F(x) — одной из первообразных функции f(x), определённой на интервале (−3; 5). Найдите количество решений уравнения f(x)=0 на отрезке [−2; 4]. 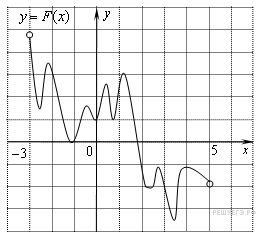 8. На клавиатуре телефона 10 цифр, от 0 до 9. Какова вероятность того, что случайно нажатая цифра будет чётной? Часть 2. 9. Найдите наибольшее значение функции  на отрезке  10. а) Решите уравнение  б) Найдите все корни этого уравнения, принадлежащие промежутку  11. Решите неравенство:  ВАРИАНТ 2. Часть 1. 1. Найдите значение выражения:  2. Решите уравнение  .3. В правильной треугольной пирамиде SABC точка L — середина ребра AC, S — вершина. Известно, что BC = 6, а SL = 5. Найдите площадь боковой поверхности пирамиды. 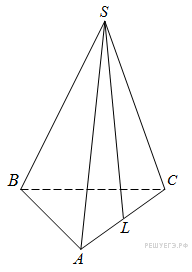 4. В цилиндрический сосуд налили 2000 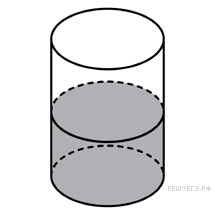 воды. Уровень воды при этом достигает высоты 12 см. В жидкость полностью погрузили деталь. При этом уровень жидкости в сосуде поднялся на 9 см. Чему равен объем детали? Ответ выразите в . 5. Основания равнобедренной трапеции равны 51 и 65. Боковые стороны равны 25. Найдите синус острого угла трапеции. 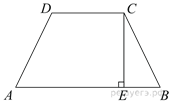 6. На рисунке изображен график функции y = f(x), определенной на интервале (−3; 9). Найдите количество точек, в которых касательная к графику функции параллельна прямой y = 12 или совпадает с ней. 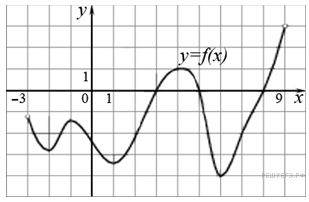 7. На рисунке изображён график некоторой функции 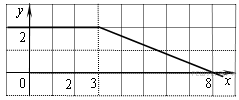(два луча с общей начальной точкой). Пользуясь рисунком, вычислите F(8) − F(2), где F(x) — одна из первообразных функции f(x). 8. Из множества натуральных чисел от 10 до 19 наудачу выбирают одно число. Какова вероятность того, что оно делится на 3? Часть 2. 9. Найдите наименьшее значение функции  на отрезке  .10. а) Решите уравнение  б) Найдите все корни этого уравнения, принадлежащие отрезку  11. Решите неравенство:  Ответы к заданиям
|
б)
