Ряды Фурье. 3. Решение задач по электротехнике
 Скачать 0.49 Mb. Скачать 0.49 Mb.
|
|
СОДЕРЖАНИЕ:
Введение Математика является одной из немногих наук, которые широко используются на практике. Любой производственно-технологический процесс не обходится без фундаментальных математических закономерностей. Эффективное применение различных инструментов математического аппарата позволяет конструировать устройства и автоматизированные агрегаты, способные выполнять операции с высоким уровнем точности, выполнять сложные расчеты и вычисления при проектировании зданий и сооружений, производить необходимые вычисления при геодезических исследованиях. Подобная тесная связь, приводит к взаимному обогащению, как самой математики, так и прикладных дисциплин. Зачастую, идеи и методы, созданные для решения частных задач, принимают общий характер и требуют строгого обоснования. Те методы, которые выдержали всесторонние проверки и весьма длительные испытания, в последствие становятся математическими теориями. В дальнейшем эти теории используются при решении более широкого круга задач, нежели те, на основе которых они были созданы. Инженерная практика в значительной мере ориентирует и стимулирует развитие математического аппарата. Именно от того, что элементы математики встречаются на производстве практически на каждом шагу, специалистам важно знать и блестяще ориентироваться в области применения тех или иных инструментов анализа и расчета. Тема представляет теоретический и практический интересы, потому что эффективное применение различных инструментов математического аппарата позволяет конструировать устройства и автоматизированные агрегаты, способные выполнять операции и с высоким уровнем точности, выполнять сложные расчёты и вычисления при проектировании зданий и сооружений, производить необходимые вычисления при геодезических исследованиях. Анализ литературных данных и результаты ранее проведенных исследований позволили выявить проблему исследования: «Какие существуют способы практического применения рядов Фурье в электротехнике и радиоэлектронике?» Актуальность и недостаточная научная проработанность данной проблемы обусловили тему исследования: «Применение рядов Фурье в электротехнике и радиоэлектронике». Цель исследования: выявить, теоретически обосновать и экспериментально проверить способы практического применения рядов Фурье в электротехнике и радиоэлектронике. Объект исследования – ряды Фурье. Предмет исследования – практическое применение рядов Фурье в электротехнике и радиоэлектронике. (п.1.2) На основании литературы была сформулирована гипотеза: применения рядов Фурье в электротехнике и радиоэлектронике решат массу важных задач. Исходя из цели и предмета исследования, для доказательства гипотезы были поставлены следующие задачи: Провести анализ литературы. 1п. Выявить применение рядов Фурье в технических науках. 2п. Провести опытно экспериментальную работу способов практического применения рядов Фурье в электротехнике и радиоэлектронике. п.3-4 Для достижения цели и решения поставленных задач применен комплекс методов исследования: – теоретические: изучение и анализ литературы и научно-исследовательских работ по теме исследования, анализ, сравнение; – эмпирические: наблюдения, проведение опытно-экспериментальной работы. Глава I. Практическое применение рядов Фурье в электротехнике и электронике 1.Ряды Фурье Рядом Фурье периодической функции 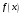 с периодом 2l, определённой на сегменте с периодом 2l, определённой на сегменте 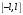 , где , где 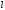 произвольное число, называется ряд произвольное число, называется ряд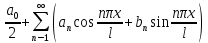 , ,где 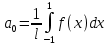 , , 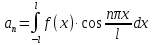 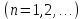 , ,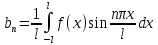 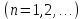 . .При этом пишут так: 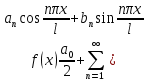 ). ).Ряд Фурье функции f(x) не всегда имеет f(x) своей суммой, если даже сходится. Достаточные условия разложимости функции в ряд Фурье Терема Дирихле. Пусть функция f(x) на сегменте 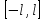 имеет конечное число экстремумов и является непрерывной за исключением конечного числа точек разрыва 1 рода. Тогда ряд Фурье для этой функции сходится в каждой точке сегмента имеет конечное число экстремумов и является непрерывной за исключением конечного числа точек разрыва 1 рода. Тогда ряд Фурье для этой функции сходится в каждой точке сегмента 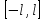 и сумма S(x) этого ряда: и сумма S(x) этого ряда:1) S(x)= f(x) во всех точках непрерывности функции f(x), лежащих внутри сегмента 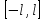 ; ;2) 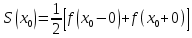 , где , где 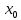 - точка разрыва 1 рода функции f(x); - точка разрыва 1 рода функции f(x);3) 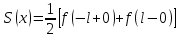 на концах промежутка, то есть при на концах промежутка, то есть при 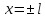 . .Ряд Фурье функции периода 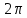 , определённой на сегменте , определённой на сегменте 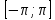 Если функция f(x)задана на сегменте 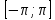 , то при выполнении на этом сегменте условий Дирихле указанная функция может быть представлена в виде ряда Фурье , то при выполнении на этом сегменте условий Дирихле указанная функция может быть представлена в виде ряда Фурье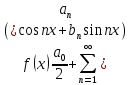 , ,где  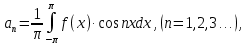 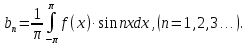 В точках разрыва функции f(x) и в концах 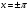 интервала сумма ряда Фурье определяется аналогично тому, как это имеет место при разложении в интервале (-l;l). интервала сумма ряда Фурье определяется аналогично тому, как это имеет место при разложении в интервале (-l;l).ФункцияF(x), совпадающая с f(x) в интервале (- 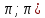 и удовлетворяющая для каждого х условию F(x+2 и удовлетворяющая для каждого х условию F(x+2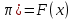 , называется периодическим продолжением функции f(x)на всю ось х. , называется периодическим продолжением функции f(x)на всю ось х.Неполные ряды Фурье (Случаи упрощения ряда Фурье) Выражение для ряда Фурье f(x) 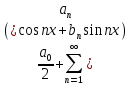 может быть записано более простым образом, если функция f(x), разлагаемая в ряд Фурье, удовлетворяет в промежутке может быть записано более простым образом, если функция f(x), разлагаемая в ряд Фурье, удовлетворяет в промежутке 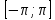 некотором условиям. некотором условиям.Случай чётной функции Если функцияf(x) - чётная (то естьf (-x)= f (x)), то 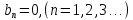 , ,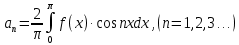 Случай нечётной функции Если функция f(x) - нечётная (то есть f (-x)= f (x)), то 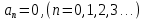 , ,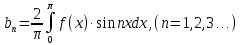 . .Разложение в ряд Фурье функций, заданных на полупериоде Функция, заданная в интервале (0; 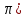 , может быть разложена в зависимости от требований либо только в ряд косинусов, либо только в ряд синусов. Для этого она должна быть продолжена в интервале (- , может быть разложена в зависимости от требований либо только в ряд косинусов, либо только в ряд синусов. Для этого она должна быть продолжена в интервале (-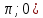 либо как чётная, либо как нечётная. либо как чётная, либо как нечётная.Функция, заданная в интервале (0; 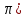 , может быть разложена в ряд Фурье бесконечным числом способов, смотря по тому, как построено её продолжение в интервал (- , может быть разложена в ряд Фурье бесконечным числом способов, смотря по тому, как построено её продолжение в интервал (-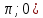 . . Комплексная форма ряда Фурье 1. Если функция f(x) задана на сегменте 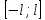 , где , где 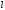 произвольное число, то при выполнении на этом сегменте условий Дирихле указанная функция может быть представлена в комплексной форме в виде суммы ряда Фурье произвольное число, то при выполнении на этом сегменте условий Дирихле указанная функция может быть представлена в комплексной форме в виде суммы ряда Фурьеf(x)= 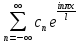 , где , где 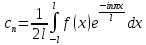 . . 2. Если функция f(x) задана на сегменте 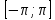 , то при выполнении на этом сегменте условий Дирихле указанная функция может быть представлена в комплексной форме в виде суммы ряда Фурье , то при выполнении на этом сегменте условий Дирихле указанная функция может быть представлена в комплексной форме в виде суммы ряда Фурьеf(x)= 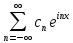 где где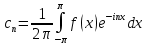 . .Такая форма записи тригонометрического ряда удобна своей краткостью. Разложение в ряд Фурье - это когда в качестве базисных функций используются так называемые синусоидальные и косинусоидальные функции. Что это за функции, можно понять, если взглянуть на движение стрелок часов ( рис.1). 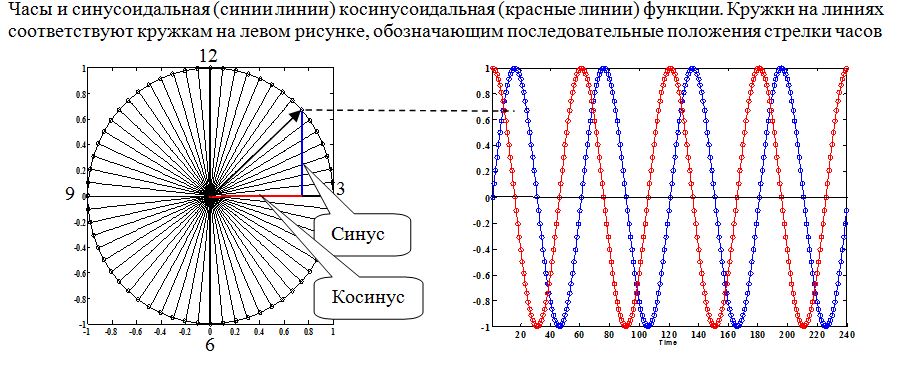 Рисунок 1. Вот как выглядят косинусоидальные (слева) и синусоидальные (справа) функции разных частот. Частота увеличивается сверху вниз. 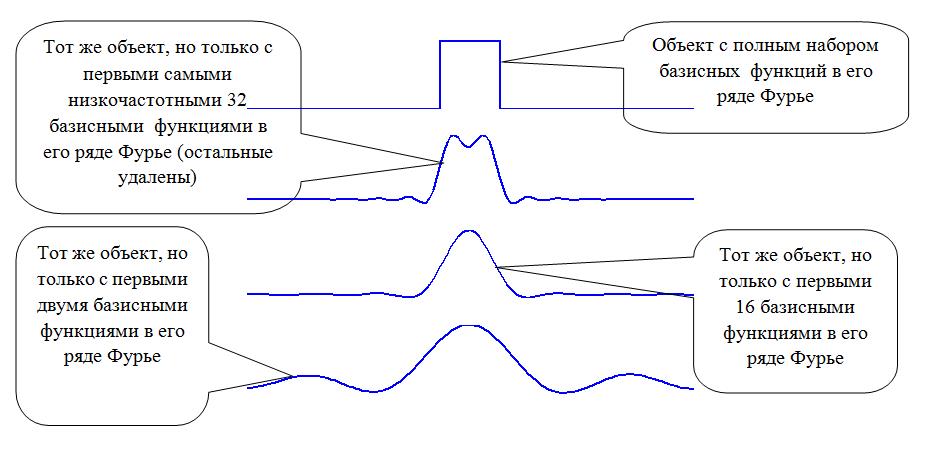 Рисунок 2.  Рисунок 3. На этих рисунках видно, что с потерей своих высокочастотных синусоидальных составляющих объект начинает уширяться и терять четко очерченную форму. Про изображение мы говорим, что оно становится размытым, нечётким. Это явление хорошо знакомо всем, кто потерял остроту зрения и вынужден пользоваться очками. Очки способны в какой-то мере восстановить интенсивность высокочастотных компонент изображений, ослабляемых оптикой глаза людей с частичной потерей остроты зрения. Ухудшение слуха с возрастом тоже, как правило, объясняется тоже ослаблением чувствительности слухового аппарата к высокочастотным составляющим звуков. Степень такого ухудшения измеряется при подборе слуховых аппаратов. Электротехника — область техники, связанная с получением, распределением, преобразованием и использованием электрической энергии. Колебания – это движение тела, в ходе которого оно многократно движется по одной и той же траектории и проходит при этом одни и те же точки пространства. Примерами колеблющихся объектов могут служить - маятник часов, струна скрипки или фортепиано, вибрации автомобиля. Колебания играют важную роль во многих физических явлениях за пределами области механики. Например, напряжение и сила тока в электрических цепях могут колебаться Тригонометрические ряды Фурье имеют широкое применение в электротехнике и радиотехнике. С их помощью изучают периодические процессы. Простейшим видом колебательного процесса являются простые гармонические колебания, которые описываются уравнением: 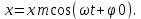
Здесь x – смещение тела от положения равновесия, xm – амплитуда колебаний, т. е. максимальное смещение от положения равновесия, ω – циклическая или круговая частота колебаний, t – время. Величина, стоящая под знаком косинуса φ = ωt + φ0 называется фазой гармонического процесса. При t = 0 φ = φ0, поэтому φ0 называют начальной фазой. Минимальный интервал времени, через который происходит повторение движения тела, называется периодом колебаний T. Физическая величина, обратная периоду колебаний, называется частотой колебаний: 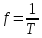 Частота колебаний f показывает, сколько колебаний совершается за 1 с. Единица частоты – герц (Гц). Частота колебаний f связана с циклической частотой ω и периодом колебаний T соотношениями: 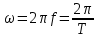
2. Применение рядов Фурье при решении задач в электротехнике Рассмотрим на конкретном примере возможности практического применения разложения в ряд Фурье. На Рис.4 представлен график температуры атмосферы. Этот график отображает среднесуточную температуру, изменяемую в течение одного года, количество данных- 365. 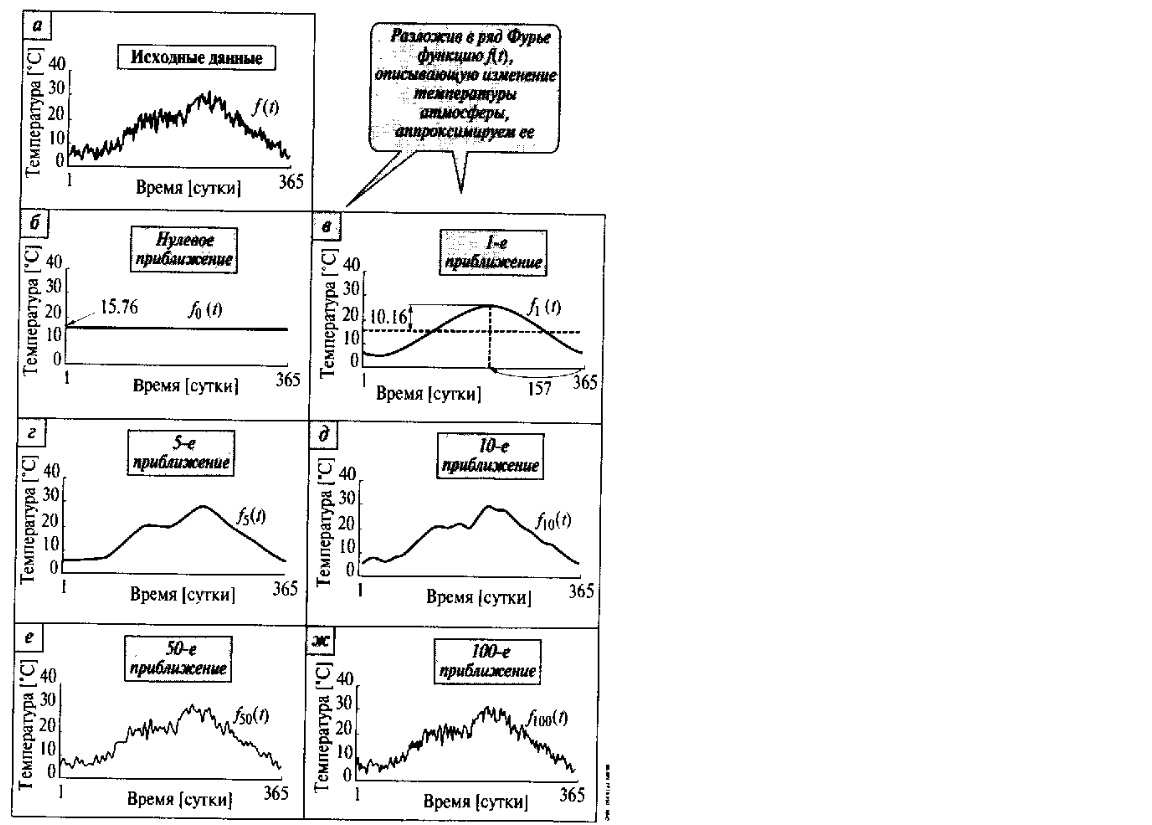 Рисунок 4. Рисунок 4.Представим в виде таблицы коэффициенты Фурье, полученные в результате вычислений (Табл. 5). В этой таблице записаны коэффициенты лишь 10-й гармоники, но в действительности они вычисляются для всех гармоник. Обозначим функцию, приближающую функцию f(t) с помощью nпервых гармоник как 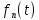 . .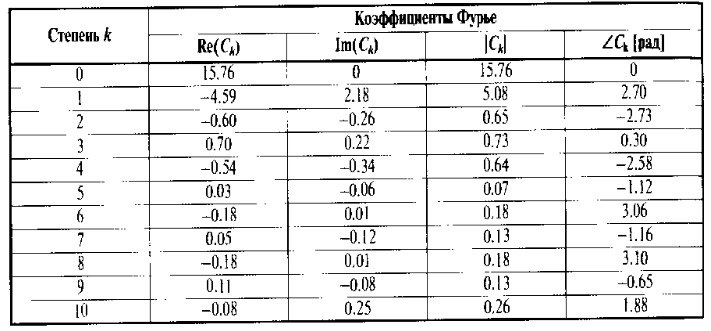 Рисунок 5. В первую очередь попробуем аппроксимировать этот сигнал постоянной составляющей, т.е. константой 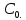 В этом приближении функция f(t) будет равна В этом приближении функция f(t) будет равна 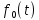 и согласно выражению и согласно выражению 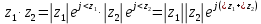 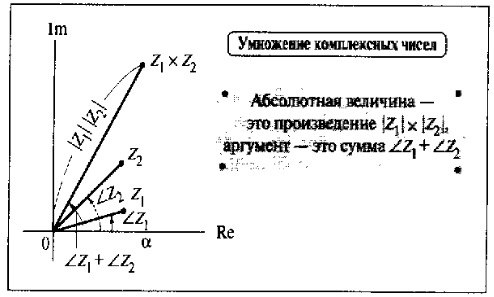 Рисунок 6. примет вид: 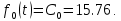 На Рис.4.б эта функция представлена графически в виде одной прямой линии, не зависящей от времени t. Кстати обратим внимание на то, что 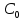 обязательно является действительным числом и отражает постоянную составляющую сигнала, в нашем случае- среднюю температуру в течение года. обязательно является действительным числом и отражает постоянную составляющую сигнала, в нашем случае- среднюю температуру в течение года.На следующем этапе прибавим первую гармонику к функции 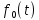 и получим функцию и получим функцию 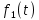 ( первое приближение функцииf(t)): ( первое приближение функцииf(t)):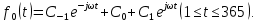 Так как период T равен 365 дням, вычислим 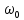 - угловую частоту основной гармоники: - угловую частоту основной гармоники: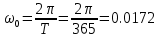 (рад/день). Ранее в выражении (4б) мы уже представили функцию f(x) с помощью амплитуд коэффициентов Фурье (рад/день). Ранее в выражении (4б) мы уже представили функцию f(x) с помощью амплитуд коэффициентов Фурье 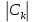 и фаз гармоник и фаз гармоник 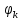 : :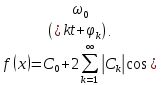 Поэтому функцию 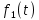 можно выразить как можно выразить как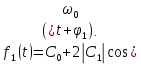 Следовательно , подставив значения коэффициентов Фурье из Табл.5, получим 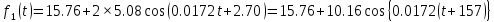 . .График функции 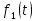 представлен на Рис.4.в в виде синусоиды, приблизительно отображающей общее изменение температуры в течение одного года. представлен на Рис.4.в в виде синусоиды, приблизительно отображающей общее изменение температуры в течение одного года.В спектре амплитуд заключается информация о величине сигнала, а в спектре фаз- информация о положении волны на оси времени. Температура меняется в течение периода, равного одному году, поэтому естественно, что составляющая первой гармоники 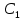 принимает большие значения. Обратим внимание на то, что форма основной гармоники явно отражает состояние летнего сезона в виде «горы» и зимнего- в виде «долины». принимает большие значения. Обратим внимание на то, что форма основной гармоники явно отражает состояние летнего сезона в виде «горы» и зимнего- в виде «долины».Итак, прибавим к первому приближению слагаемые с гармониками более высоких частот. В ряд Фурье рассматриваемой функции приближения 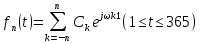 поставим значения коэффициентов Фурье из Табл.5 и графически изобразим функцию, представленную числом гармоники n (Рис.4). Из графиков становится понятно, что с увеличением числа гармоник прибавляются составляющие высоких частот, и форма сигнала постепенно приближается к исходной форме сигнала температуры. А приближение при n=100 (Рис.4.ж) практически неотличимо от исходной функции. 3. Решение задач Задача 1: Разложить в ряд фурье сигнала 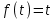 на отрезке на отрезке 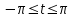 . .Решение: 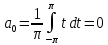 , , 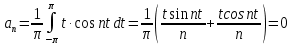 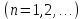 , ,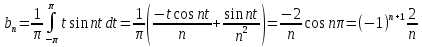 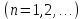 Следовательно, функцию можно представить в ряд Фурье следующим образом: 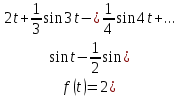 Заключение: Тема представляет теоретический и практический интересы, потому что эффективное применение различных инструментов математического аппарата в электротехнике позволяет конструировать устройства и автоматизированные агрегаты, способные выполнять операции и с высоким уровнем точности, выполнять сложные расчёты и вычисления. Список литературы : Атабеков Г.И. А92 Теоретические основы электротехники. Линейные электрические цепи: Учебное пособие. 7-е изд., стер. СПб.: Издательство «Лань», 2009. — 592 с.: ил. — (Учебники для вузов. Специальная литература Гевелюк И. В. РЯДЫ ФУРЬЕ И ИХ ПРАКТИЧЕСКОЕ ПРИМЕНЕНИЕ В ЭЛЕКТРОТЕХНИКЕ // Научное сообщество студентов XXI столетия. ТЕХНИЧЕСКИЕ НАУКИ: сб. ст. по мат. XXII междунар. студ. науч.-практ. конф. № 7(22). URL: http://sibac.info/archive/technic/7(22).pdf (дата обращения: 16.10.2016) Сборник задач по математическому анализу. Том 2. Интегралы. Ряды [Электронный ресурс]/ Л.Д. Кудрявцев [и др.].— Электрон. текстовые данные.— М.: ФИЗМАТЛИТ, 2009.— 504 c.— Режим доступа: http://www.iprbookshop.ru/12900.— ЭБС «IPRbooks», по паролю |
