8. Показатели вариации. 5. 1 Показатели вариации Понятие вариации. Расчет среднего линейного отклонения
 Скачать 344 Kb.
|
|
3. Имеются данные о вариации цен на товар «А», реализуемый на различных рынках города:  Определите: 1) среднюю цену товара на различных рынках, цену, соответствующую наибольшему объему продаж; 2) степень однородности цен на различных рынках. 4. Имеются следующие данные о коммерческих банках Российской Федерации:  На основе представленных данных рассчитайте все показатели вариации. 5. Имеются следующие данные о просроченной задолженности покупателей организаций топливной промышленности Российской Федерации в 2005 г. (на конец года):  Определите степень влияния отраслевой принадлежности организаций на вариацию просроченной задолженности и тесноту связи между признаками. Показатели вариации, способ их вычисления При изучении совокупности явления нельзя ограничиваться только нахождением средней величины. Средние величины дают обобщенную характеристику варьирующего признака, показывают типичные характеристики для изучаемой совокупности. Однако в средней величине не проявляется степень колеблемости отдельных значений признаков (вариант) вокруг среднего уровня. В зависимости от однородности в совокупности колеблемость признаков может быть большой или, наоборот, малой. Поэтому возникает необходимость в измерении вариации отдельных вариантов по отношению к средней величине. Для большей убедительности приведем два ряда набора чисел: I ряд — 6, 10,14,26,34; II ряд— 14,16,18,20,22. Определим среднюю арифметическую (  ):для I ряда  ; для II ряда .Таким образом, два совершенно различных ряда имеют одну и ту же среднюю (ха= 18). Отсюда следует, что эти средние не характеризуют внутреннего содержания совокупности/ В результате простого обозрения видно, что в первом ряду колеблемость признаков больше, чем во втором. Для измерения пестроты, колеблемости (вариации) изучаемого признака в данной совокупности статистики применяются различные показатели. Рассмотрим сначала размах вариации (R). Размах колебаний (R)— это разность между наибольшей и наименьшей вариантной  Для предыдущего примера амплитуда вариации составляет: R1(I ряда) = 34 - 6 = 28 единиц;R11(IIряда) = 22 - 146 = 8 единиц. Таким образом, можно сделать вывод, что первый ряд распределения имеет значительно большую амплитуду вариант, чем второй ряд распределения. Однако ограничиться определением вариации будет неверно, потому что этот показатель дает только общее, внешнее представление о колеблемости, о пределах вариации, но не характеризует степени колебаний данного признака в этих пределах. Размах вариации улавливает только крайние отклонения, но не отражает размера отклонений всех вариант. По показателям отклонений оценивается надежность вычисленной средней величины, т. е. выявляется, можно ли пользоваться рассчитанной средней величиной. 8. Среднее квадратическое отклонение Для определения степени колеблемости признаков используется среднее квадратическое отклонение, широко применяемое в экономических расчетах. Среднее квадратическое отклонение бывает простое и взвешенное. Оно обозначается буквой σ. 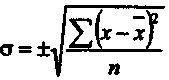 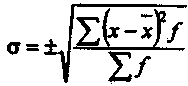— простое квадратическое отклонение;  —взвешенное квадратическое отклонение.Рассмотрим порядок вычисления взвешенного среднего квадратического отклонения.
 Таким образом, получается дисперсия, или средний квадрат отклонений.
 Пример. Произведем вычисление простого и взвешенного среднеквадратического отклонения. В табл. 12 показано распределение кип шерсти по массе при отгрузке. Таблица .12 Распределение кип шерсти при отгрузке
Требуется определить СА простую и взвешенную, среднее квадратическое отклонение простое и взвешенное.
 Подставим значения:  2. Среднее квадратическое простое отклонение (не взвешенное) определяем по формуле: 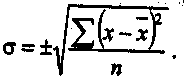 Для расчета квадратического отклонения построим расчетную таблицу(таб. .13). Таблица .13 Данные для расчета квадратического отклонения
Что характеризует полученное квадратическое отклонение? Масса отдельных кип шерсти отклоняется от средней (96 кг) в одних случаях на большую величину, в других— на меньшую. В среднем это отклонение от средней составляет ±7,7 кг. Из этих данных видно и другое: простое среднее квадратическое отклонение выражается в тех же именованных числах, что и средняя величина. Поэтому оно составляет так называемое абсолютное отклонение от средней величины. По данным примера рассчитаем также среднее квадратическое отклонение (взвешенное) для характеристики ряда распределения с неравными частотами. Для этого примем во внимание количество отгруженных кип, которые будут составлять частоты(f). Расчет производим по формуле:  Построим расчетную таблицу (табл. .14). Сначала определяем среднюю арифметическую взвешенную:  Рассчитаем среднее квадратическое отклонение (взвешенное): 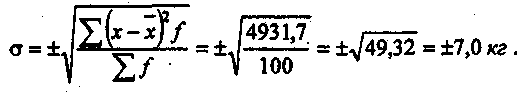 Расчетные данные для определения взвешенного квадратического отклонения
Следовательно, средняя колеблется в пределах 96,3 кг ±7,0 кг. К вопросу 7. Коэффициент вариации До сих пор мы изучали показатели, которые были выражены в абсолютных величинах, т. е. в тех же именованных числах, что и варьирующий признак (в данном примере — в килограммах). Однако квадратическое отклонение, как и всякая абсолютная величина, недостаточно наглядно характеризует колеблемость вариант вокруг средней величины. О том, насколько велико это отклонение, можно судить только при расчете коэффициента вариации. Коэффициент вариации представляет собой отношение среднего квадратического отклонения к средней арифметической и выражается в процентах. Коэффициент вариации рассчитывается по формулам:  а) для среднего квадратического отклонения (простого): и в нашем примере составит:   б) для среднего арифметического отклонения (взвешенного): т.е.  Коэффициент вариации является отвлеченным числом и поэтому он наиболее удобен в измерении вариации признаков. Кроме того, этот показатель можно использовать для сравнения колеблемости совокупностей как с одинаковыми, так и с различными признаками. Пример. Предположим, что мы определяем колеблемость веса одной кипы шерсти по двум партиям путем сравнения коэффициентов вариации I и II партий. Это будет сравнение колеблемости совокупностей, имеющих одинаковые признаки. Или, например, требуется сравнить, что больше колеблется: средний объем товарооборота одной торговой фирмы или средний размер площади торгового зала, т. е. сравниваем совокупности с разными признаками и определяем степень колеблемости этих различных признаков путем вычисления коэффициентов вариации. Дисперсия Дисперсия — это средний квадрат отклонения всех значений признака ряда распределения от средней арифметической. Именно дисперсия и среднее квадратическое отклонение являются основными наиболее употребляемыми показателями вариации.  Обозначается дисперсия буквой где х — значение признака;  - средняя арифметическая; п — численность совокупности. Но  Поделив это выражение на п, учтем, что  . Тогда т. е. дисперсия равна разности среднего квадрата вариантов и квадрата их средней (подразумевая здесь под "средней" среднюю арифметическую). И, наконец,  Заменяя в формуле определения дисперсии (Dx) среднее суммами, разделенными на численность совокупности, получим формулу: 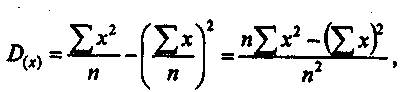 имеющую некоторые технические преимущества для ее вычисления. При ее применении округление производится только один раз и в самом конце вычисления. Пример. В табл. 15 приведены данные для расчета дисперсии и среднего квадратического отклонения на примере стажа продавцов торговой фирмы "Элегант", работающих в двух ее магазинах. Для 1-го магазина: 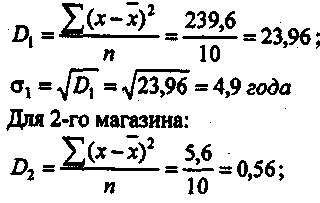 Таблица.15Данные для расчета дисперсии и среднего квадратического отклонения по стажу продавцов в двух магазинах фирмы "Элегант"
 Таким образом, стаж продавцов отклоняется от среднего для первого магазина на 4,9 года, а для второго магазина — 0,75 года. Формула дисперсии для вариационного ряда с вариантами х и частотами/будет иметь вид: 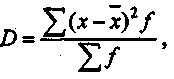 где х — значение признака;  — средняя арифметическая; f— частота. | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
.
.
. Затем полученные отклонения суммируют.
), кг
