8. Показатели вариации. 5. 1 Показатели вариации Понятие вариации. Расчет среднего линейного отклонения
 Скачать 344 Kb.
|
|
Свойства дисперсии Дисперсия обладает рядом простых свойств: 1. D(a)= 0 — дисперсия постоянной величины равна нулю. 2.  — дисперсия не меняется, если все варианты увеличить или уменьшить на одно и то же число.3.  — постоянный множитель выносится за знак дисперсии возведенным в квадрат. Или: если все варианты умножить на число а, дисперсия увеличиться в  раз. — это свойство носит название свойства минимальности дисперсии от средней. Дисперсия от средней меньше, чем средний квадрат отклонения от любого числа  на  .Использование свойств дисперсии позволяет упрощать ее расчеты, особенно в тех случаях, когда вариационный ряд составляет арифметическую прогрессию или имеет равные интервалы. В этих случаях сначала находят дисперсию от условного нуля, а затем используют 4-е свойство дисперсии, переходят к дисперсии от средней. Правила сложения дисперсий Если совокупность состоит из нескольких частей, то можно определить в пределах каждой не только среднюю величину, но и дисперсию  (частную дисперсию). Выясним как связана с ними общая диспепсия по всей совокупности D. Обозначим частные средние  , а общую  .Суммирование в рамках i-й части обозначим 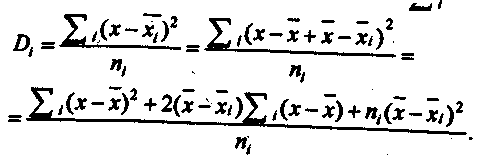  Но  Сделав подстановку, найдем  Отсюда Чтобы получить общую дисперсию, надо 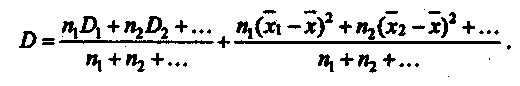 просуммировать все и разделить на их количество n=n1+n2+…Т.о., Обозначив через δi отклонение простой средней от общей, получим: 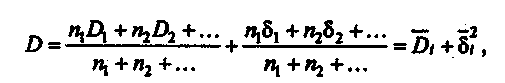 т. е. общая дисперсия равна сумме средней и частных дисперсий (взвешенной по численности соответственных частей) и среднего квадрата отклонения частных средних от общей средней (тоже соответственно взвешенного), или общая дисперсия равна сумме средней из частных дисперсий и дисперсии частных средних. Это есть правило сложения дисперсий. Оно означает, что общая дисперсия складывается из двух слагаемых, одно из которых измеряет вариацию внутри частей совокупности, а второе— различия (вариацию) между этими частями (представленными средними). Рассмотрим более подробно смысл каждой из дисперсий. Пусть имеются данные о средних и дисперсиях заработной платы по менеджерам, работающим в двух компаниях (табл. .16). О 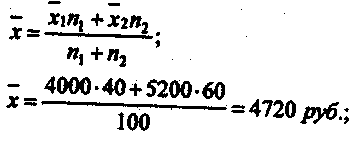 пределим общую среднюю заработную плату х и дисперсию заработной платы Dдля всей совокупности менеджеров на основе правил сложения средних дисперсий Т 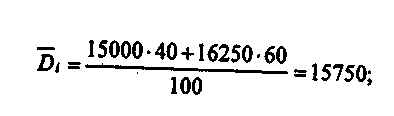 аблица.16 Данные для определения средних и дисперсий по заработной плате компаний "Бест" и Иванов К°"
 Отсюда D- 15750 + 384 -16134. Каждая из исчисленных дисперсий имеет определенный смысл. Общая дисперсия (D) показывает величину вариации заработной платы, которая вызвана всеми факторами, влияющими на размер заработной платы: различиями в оплате, квалификации, индивидуальных качеств менеджеров и т. п. Внутригрупповые, частные дисперсии показывают величину вариации, которая вызвана любыми причинами, например функциональными областями работы менеджеров. Средняя из частных дисперсий, естественно, так же отражает вариацию, вызванную прочими кроме различий в специализации менеджеров причинами, но уже не по отдельным группам менеджеров, а в среднем по всей совокупности менеджеров. Межгрупповая дисперсия, или дисперсия групповых средних, характеризует вариацию групповых средних, которая обусловлена различиями групп менеджеров по разным компаниям. Если сгруппировать менеджеров внутри компании по другому признаку, оказывающему влияние на заработок (например, по уровню квалификации), то можно из внутригрупповых дисперсий выделить дисперсию, показывающую величину вариации, вызванной вторым группировочным признаком, и дисперсию остаточную, характеризующую вариацию за счет всех причин, кроме двух группи-ровочных признаков. Теоретически такую комбинационную группировку можно продолжить до тех пор, пока не будут исчерпаны все причины, воздействующие на исследуемый признак. Общая дисперсия при этом будет представлена как сумма дисперсий, характеризующих вариацию, вызванную каждой из причин, т. е.  Доля каждой из полученных дисперсий в общей дисперсии покажет степень влияния соответствующего признака на исследуемый результативный признак. Именно поэтому правило сложения дисперсий находит широкое применение в анализе взаимосвязей и зависимостей. Вопросы для самоконтроля 1.. Что такое средние величины и каковы их роль и значение?
10. Какие существуют показатели вариации и для каких целей они применяются? |
)