Самостоятельная по математике вернее практическая решённая на 25 баллов от руки Чупрова валентина. математика 5 ззадддание. 5 Многогранники и площади их поверхностей. Объем многогранников Задание 2

• Название: 5 Многогранники и площади их поверхностей. Объем многогранников Задание 2
• Анкор: Самостоятельная по математике вернее практическая решённая на 25 баллов от руки Чупрова валентина
• Дата: 05.12.2022
• Размер: 126.3 Kb.
• Имя файла: математика 5 ззадддание.doc
• Тип: Самостоятельная работа; #829108

Самостоятельная работа по теме 5.2. Многогранники и площади их поверхностей. Объем многогранников

Задание 2. Два ребра прямоугольного параллелепипеда, выходящие из одной вершины, равны 3 и 4. Площадь поверхности этого параллелепипеда равна 94. Найдите третье ребро, выходящее из той же вершины.
Ответ:с поверхности = 2(Sa+Sв+Sс), где Sa, Sв и Sc - это площади боковых(заштрихованных) поверхностей

Пусть х-третье ребро

Sа=4*3=12;

Sв=3х

Sс=4х

94=2(12+3х+4х)

47=12+7х

7х=35

х=5

третье ребро = 5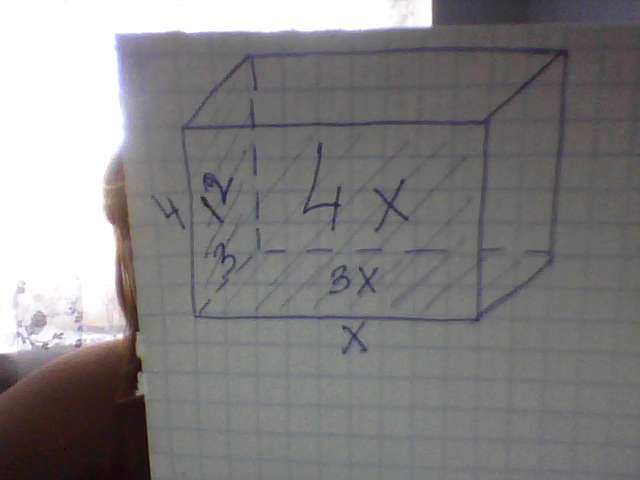

 


Задание 3. Два ребра прямоугольного параллелепипеда, выходящие из одной вершины, равны 1, 2. Площадь поверхности параллелепипеда равна 16. Найдите его диагональ.

Ответ:

Пусть х - длина третьего ребра. Тогда площадь поверхности S=16, следовательно и
2(1•2 +х + 2х) = 16
2(2+3х)=16
4+6х=16
6х=12
х=2
Значит, ребра равны 1, 2 и 2.
Рассмотрим грань с ребрами 2 и 2.
Диагональ этой грани:
с=корень из (2^2 + 2^2)=корень из 8= 2 корня из 2.
Рассмотрим сечение параллелепипеда, проходящее через диагональ с и 2 ребра длиной 1 каждое. Мы видим прямоугольник со сторонами 1 и 2 корня из 2.
Его диагональ d=корень из [1^2 + (2 корня их 2)^2]= корень из (1+8)= корень из 9= 3.
Диагональ параллелограмма равна 3.

Задание 4. Ребра прямоугольного параллелепипеда, выходящие из одной вершины, равны 1, 2, 3. Найдите его площадь поверхности.

Ответ:Площадь полной поверхности прямоугольного параллелепипеда: Sп=2(ab+bc+ac) 
а=1 
b=2 
c=3 
S=2(1*2+2*3+1*3)

Задание 5. Найдите площадь боковой поверхности правильной шестиугольной призмы, сторона основания которой равна 5, а высота – 10
Площадь боковой поверхности призмы равна сумме площадей всех ее боковых граней:

​\( S_{бок}=6S_{гр} \)​

Подставим числовые значения в формулу.​

​\( S_{бок}=6*5*10=300 \)​.

Ответ к задаче

Ответ: 300.

Задание 6. Найдите площадь поверхности прямой призмы, в основании которой лежит ромб с диагоналями, равными 6 и 8, и боковым ребром, равным 10. 

S полной поверхности= 2*S основания + S боковой поверхности S основания = 1/2 * 6 * 8= 24 S боковой поверхности = a * H (a -  сторона ромба, H - боковое ребро) a = корень из (6*6+8*8)= 10 (по теореме Пифагора) S боковой поверхности = 10 * 20 = 200 S полной поверхности = 2 * 24 + 200 = 248 Ответ: 248 

Задание 7. Основанием прямой треугольной призмы служит прямоугольный треугольник с катетами 6 и 8. Площадь ее поверхности равна 288. Найдите высоту призмы. 

РЕШЕНИЕ:

Площадь поверхности прямой треугольной призмы равна сумме 2 площадей основания и площади боковой поверхности призмы:

Sпризмы = Sбок.пов + 2Sосн

Площадь основания равна площади прямоугольного треугольника с катетами 6 и 8. Площадь прямоугольного треугольника равна половине произведения катетов:

Sосн = 1/2 ⋅ 6 ⋅ 8 = 24

Найдем площадь боковой поверхности призмы, вычтя из площади полной поверхности призмы 2 площади основания:

Sбок.пов = Sпризмы – 2Sосн = 288 – 2 ⋅ 24 = 288 – 48 = 240

Площадь боковой поверхности прямой треугольной призмы равна периметру основания, умноженному на высоту. Чтобы найти высоту призмы, нужно вычислить периметр основания. Катеты прямоугольного треугольника, лежащего в основании, известны, осталось найти его гипотенузу по теореме Пифагора:

√62 + 82 = 10

Тогда высота прямой треугольной призмы равна:

Sбок.пов / (6 + 8 + 10) = 240 / 24 = 10

ОТВЕТ: 10

Задание 8. 

В правильной треугольной призме, все ребра которой равны 3, найдите угол между прямыми ВВ1 и АС1 Ответ дайте в градусах.

АС₁ и ВВ₁ - скрещивающиеся прямые. Чтобы показать угол между скрещивающимися прямыми, надо одну их них параллельно перенести, тобы получились пересекающиеся прямые. ВВ₁ || АА₁,  АА₁∩АС₁, значит нам нужен ∠А₁АС₁, этот угол является  углом прямоугольного равнобедренного треугольника А₁АС₁, ∠А₁АС₁, = 45°

Задание 9. В правильной треугольной призме ABCA1B1C1 стороны оснований равны 2, боковые рёбра равны 5. Найдите площадь сечения призмы плоскостью, проходящей через середины рёбер AB, AC, A1B1 и A1C1. 
К₁



А

В

С

А₁

В₁






С₁



К



В правильной треугольной призме ABCA1B1C1 стороны оснований равны 2√3, боковые ребра равны 5. Найдите площадь сечения призмы плоскостью, проходящей через середины ребер AB и A1B1 и точку C

Задание 10. Основанием прямой треугольной призмы служит прямоугольный треугольник с катетами 6 и 8, боковое ребро равно 5. Найдите объем призмы. 

Объем призмы находится по формуле  , где   - площадь основания призмы;   - ее высота. Найдем площадь основания прямоугольного треугольника с катетами 6 и 8 по формуле



и объем призмы равен

.

Задание 11. Через среднюю линию основания треугольной призмы, объем которой равен 32, проведена плоскость, параллельная боковому ребру. Найдите объем отсеченной треугольной призмы. В основании призмы лежит треугольник, средняя линия проходит через середины двух соседних сторон треугольника и параллельна третьей стороне. Длина средней линии в 2 раза меньше стороны, которой она параллельна. Таким образом, получаем, что меньший треугольник (основание отсеченной призмы) имеет линейные размеры в 2 раза меньшие, чем исходный треугольник. Следовательно, площадь малого треугольника в 4 раза меньше площади исходного. Высоты исходной и отсеченной пирамид равны. Получаем, что объем отсеченной пирамиды, равный   меньше исходного объема   в

.

Так как исходный объем  , то

.

Ответ: 8.

Задание 12. 

В правильной четырехугольной пирамиде АВCDS точка O – центр основания, S – вершина, SO=30, SA=34. Найдите длину отрезка АС.

треуг SAO-прямоуг

АО = SA в квадрате - SO в квадрате

АО = 34 в квадрате - 30 в квадрате

АО=16

АС=1/2 АО

АС=16*2=32

Задание 13. В правильной треугольной пирамиде SABC точка M – середина ребра AB, S – вершина. Известно, что BC = 3, а площадь боковой поверхности пирамиды равна 45. Найдите длину отрезка SM.

 

В основании правильной треугольной пирамиды SABC лежит равносторонний треугольник, следовательно, AB=BC=AC=3. Боковыми гранями пирамиды являются равнобедренные треугольники и стороны AS=SB=SC. Тогда отрезок SM – высота треугольника ABS. Площадь боковой поверхности пирамиды можно выразить формулой

,

откуда



и

.

Ответ: 10.