5. Основные уравнения гидростатики и его физический смысл
 Скачать 9.76 Mb.
|
|
25. турбулентное движение. При увеличении скорости слоистое течение жидкости нарушается и движение становится беспорядочным, бесформенным- турбулентным. Критерий, характеризующий режим движения, называется числом Рейнольдса и определяется по следующей формуле: 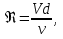 гдеV – средняя скорость потока;d – диаметр потока v- коэффициент кинематической вязкости. Если в потоке жидкости скорость постепенно увеличивать, то смена ламинарного режима на турбулентный произойдет если число Рейнольдса достигнет верхнего критического значения равного 13800. Если скорость уменьшать, то турбулентный режим перейдет в ламинарный при нижнем критическом значении 2320. Область, заключенная между верхним и нижним значения числа Рейнольдса, называется переходной областью или областью неустойчивого режима, в которой может установиться как ламинарный, так и турбулентный режимы. 26. Шероховатые стенок труб. Потери напора по длине происходят за счет вязкости самой жидкости и трения о шероховатые поверхности. Потери напора по длине определяются по формуле Дарси-Вейсбаха: 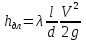 ,где λ - коэффициент гидравлического трения, l – длина участка трубопровода, d – внутренний диаметр трубопровода, V - средняя скорость потока жидкости. Потери напора, происходящие за счет деформации потока в различных гидравлических устройствах, называются потерями в местных сопротивлениях и определяются по формуле Вейсбаха: 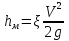 где ξ - коэффициент местных сопротивлений, справочная величина, для каждого типа гидравлических устройств имеет численное значение. V - средняя скорость потока. Суммарные потери определяются: 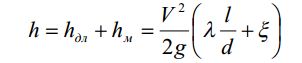 Для успешного вычисления суммарных потерь необходимо правильно определить коэффициент гидралического трения, который на прямую зависит от режима движения, а следовательно и от формирования структуры потока при каждом режиме.Формирование структуры потока при ламинарном режиме происходит в несколько этапов. На начальном этапе все слои жидкости движутся с одинаковой скоростью. Затем, в следствии трения о шероховатые твердые поверхности, происходит торможение переферийных слоев. В последствие за счет внутреннего трения идет последующее торможение слоев. Этот процесс продолжается до тех пор, пока эпюра скоростей не представит собой параболу. Минимальные скорости при этом устанавливаются по краям потока, максимальные в центре. Такое формирование потока устанавливается на участке длиной L=(20:50)d, где d – внутренний диаметр. При этом коэффициент Кориолиса принимается равным a =2, а коэффициент гидравлического трения 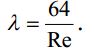 .27. Зоны гидравлических сопротивлений. Для гидравлических гладких труб : 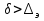 ;  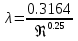, 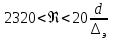Переходная зона(зона смешанного сопротивления): 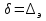 ;  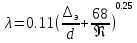, 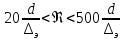Зона шероховатых труб (квадратичное сопротивление): 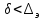 ;  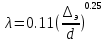, При ламинарном режиме λ зависит только от числа Рейнольдса и определяется по формуле: 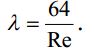28) Местные гидравлические сопротивления Они имеют место в потоках на участках резкого изменения конфигурации. В зоне местных сопротивлений происходит обтекание препятствий, возникает вихреобразование, деформация потока , на что теряется часть энергии.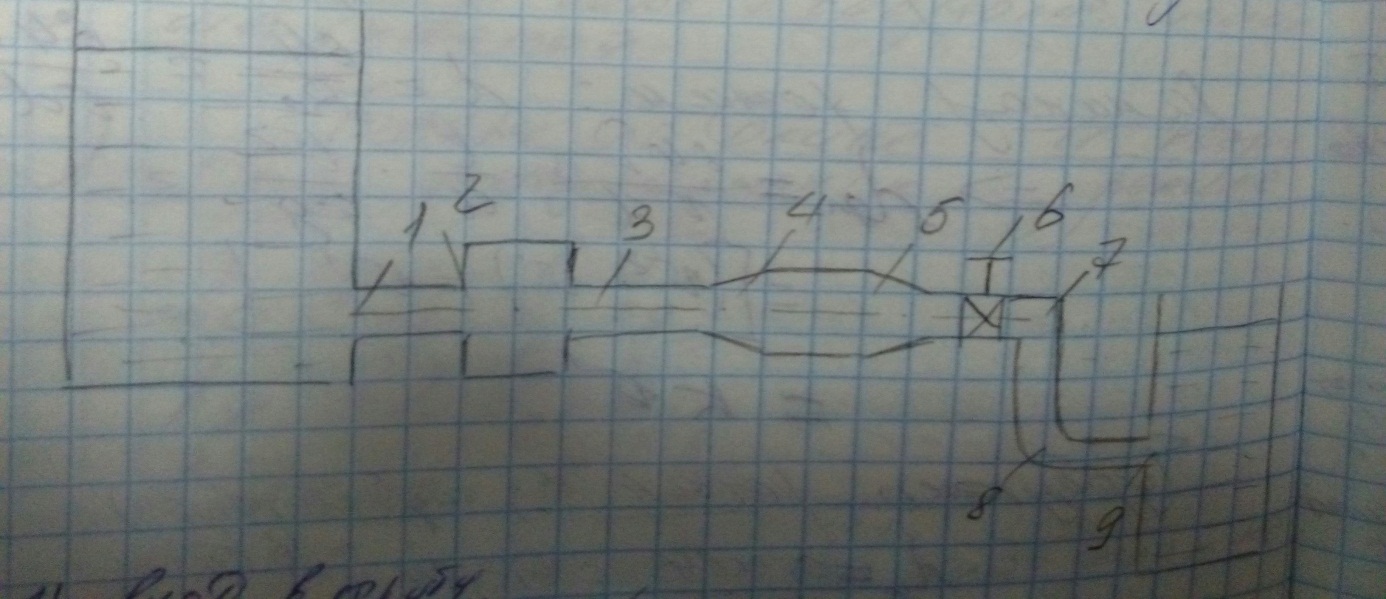 
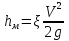где ξ - коэффициент местных сопротивлений, справочная величина, для каждого типа гидравлических устройств имеет численное значение. V - скорость за местным сопротивлением . В гидравлике общие потери :  где lэкв. –это длина такого прямолинейного участка трубопровода, при пропуске через которую такого же расхода жидкости Q возникают одинаковые местные сопротивления   29. Короткие трубопроводы и методика их расчета. Коротким считается трубопровод небольшой длины, но имеющий большое количество местных сопротивлений(масло и топливоприводы двигателей, системы охлаждения и смазки, гидроприводы станков и др. машин)  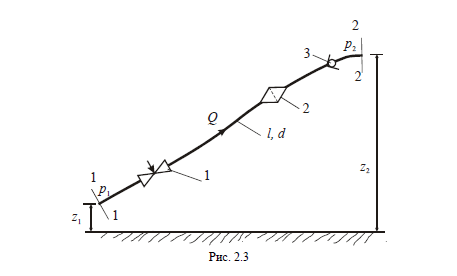   30. Основные задачи по расчету коротких трубопроводов и способы их решения. При расчетах коротких трубопроводов основной задачей является либо определение пропускной способности (расхода), либо потери напора на том или ином участке, равно как и на всей длине, либо диаметра трубопровода на заданных расходе и потерях напора. Задача на расход:   Задача на потери напора:  Задача на определения диаметра:   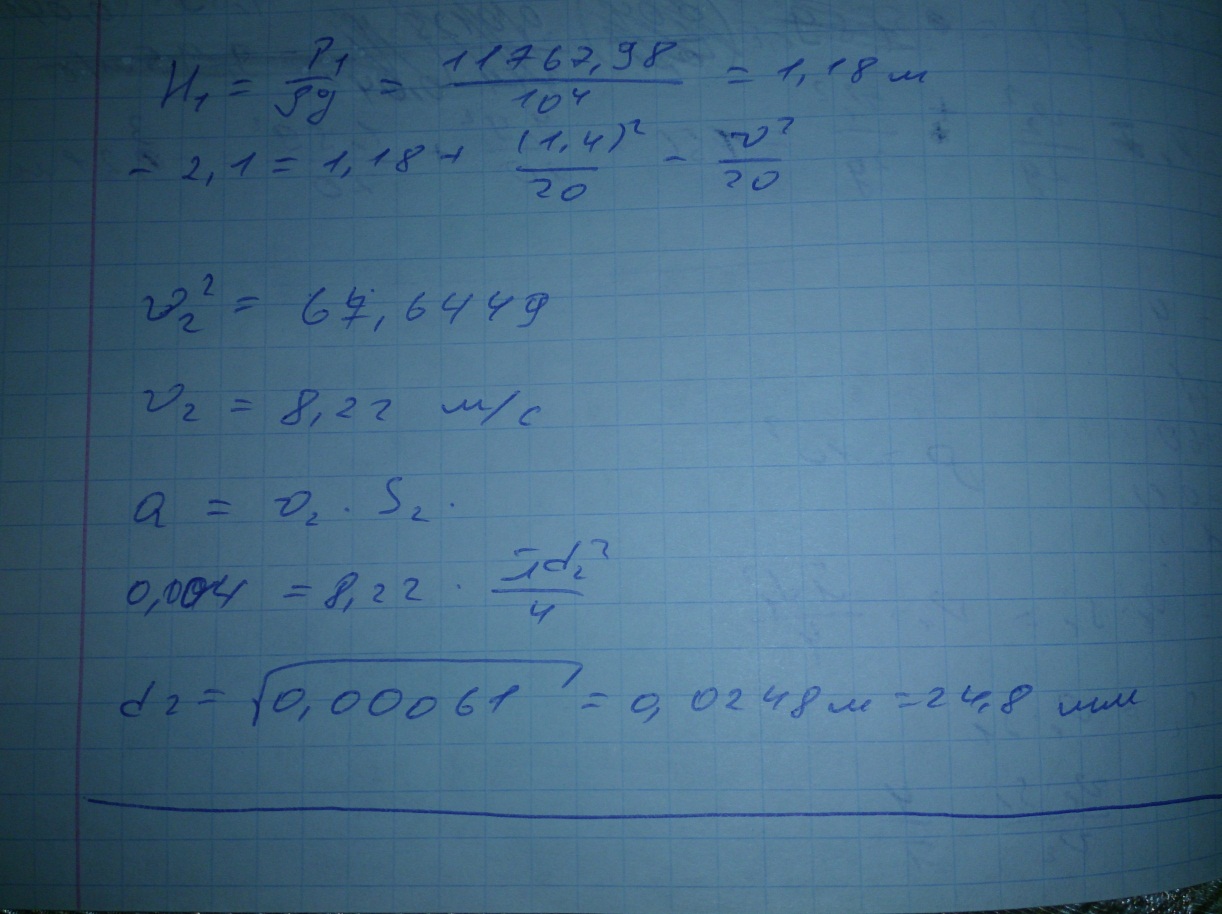 31. Основы технико-экономического расчета трубопроводов. Увеличение диаметра трубопровода уменьшает потери напора, а следовательно, снижает расход энергии при работе насосной установки. Однако при этом увеличивается стоимость трубопровода (чем больше диаметр, тем больше стоимость). Учитывая, что устройство длинных напорных трубопроводов связано со значительными капитальными затратами, вопрос о выборе диаметра трубопровода приобретает большое практическое значение и должен решаться с учетом основных факторов, влияющих на стоимость всего сооружения в целом (стоимость трубопровода, насосных установок и других сооружений), а также всех эксплуатационных расходов, связанных с работой насосных установок и самого трубопровода. Экономически наивыгоднейшим диаметром трубопровода будет такой диаметр, при котором сумма ежегодных денежных затрат (амортизационных и эксплуатационных) по данному комплексу сооружений будет наименьшей. Задача по определению экономически наивыгоднейшего диаметра трубопровода решается следующим образом: задавшись рядом значений диаметра трубопровода 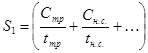 , вычисляют строительную стоимость С всех сооружений в каждом варианте. Затем исходя из расчетного срока окупаемости отдельных сооружений определяют суммарную стоимость всех сооружений в расчете на один год: Подсчитав ежегодные эксплуатационные расходы , связанные с работой трубопровода (ремонт, обслуживание), эксплуатационные расходы по насосной станции (стоимость энергии, содержание штата, ремонт и т.д.) и другим сооружениям, устанавливают размер полных ежегодных эксплуатационных расходов по всему комплексу сооружений:  Полная ежегодная стоимость данного варианта трубопровода  Минимальное значение полной стоимости соответствует экономически наивыгоднейшему диаметру трубопровода. 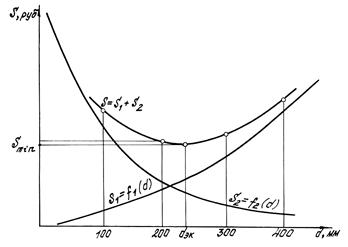 Рис.12 На рис.12 приведен типовой график вида зависимостей  .32. Расчёт коротких трубопроводов при последовательном и параллельном их соединении. Последовательное соединение трубопроводов:   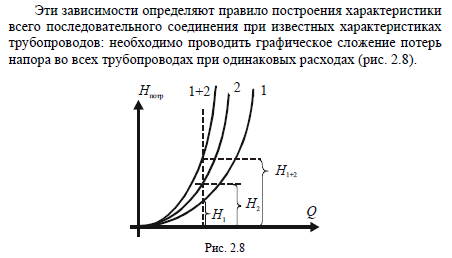  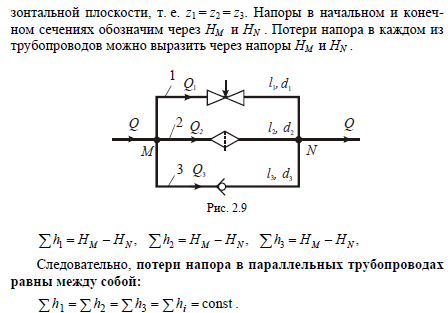 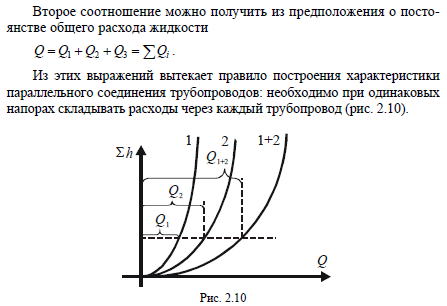 33. Основные расчеты длинных трубопроводов. Длинными считаются трубопроводы, которые имеют значительное притяжение, и в которых основным являются потери на трение, т.е. потери по длине. Отличием длинных трубопроводов от коротких является незначительность потерь напора на местное сопротивление по сравнению с потерями по длине . Поэтому при расчете длинных трубопроводов слагаемым потери на местных сопротивлениях можно пренебречь. На практике местные сопротивления учитываются введением коэффициента, который равен k=(5-10)% hl. Значением скоростного напора ввиду его малости по сравнению с пьезометрическими напорами, также можно пренебречь. При решении практических задач обычно заданной или искомой величиной является расход воды, при этом   – удельное сопротивление трубы, которое зависит от диаметра и коэффициента гидравлического трения λ. 34. Расчет водопровода. Основные задачи и способы их решения. 35. Расчет трубопроводов с насосной подачей жидкости. Для этого рассмотрим наиболее простой случай трубопровода, по которому насос перекачивает жидкость из гидробака в ёмкость или полость с заданными величинами давления и расхода. К таким ёмкостям можно отнести, например, гидроцилиндр 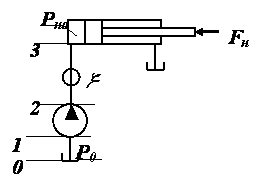 Запишем сначала уравнение Бернулли для сечений 2 и 3  Где  -атмосферное давление, суммарные потери давления во всасывающем трубопроводе (характеристика всасывающего трубопровода). Теперь запишем уравнение Бернулли для сечений 0 и 1 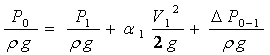 Из второго уравнения определим общий напор (энергию), которым обладает жидкость при входе в насос. Тогда второе уравнение примет вид 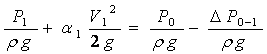 В процессе своей работы насос передаёт жидкости дополнительную энергию Hнасоса, в результате чего общий напор жидкости в сечении 2 становится равным: 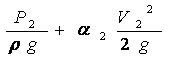 т.е. можно записать:  Выделим из полученного равенства величину насоса: 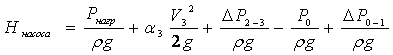 Перегруппируем члены в этом выражении:  Если принять, что: в первом слагаемом атмосферное давление P0 равно 0, второе слагаемое (скоростной напор на выходе из напорного трубопровода) можно переписать через расход и представить в виде где _ можно считать коэффициентом скоростного напора (в этом выражении Й – площадь сечения трубопровода), третье слагаемое можно представить в виде суммарной характеристики всасывающего и напорного трубопровода, то последнее выражение примет вид: 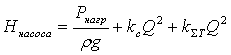 выражение представляет собой рабочую характеристику насоса Построив характеристику трубопровода и характеристику насоса можно найти так называемую рабочую точку, как точку пересечения характеристик насоса и трубопровода. Это означает, что при соответствующих этой точке давлении и расходе, будет обеспечиваться работа насоса с требуемыми характеристиками. Чтобы получить другую рабочую точку нужно или изменить рабочую характеристику насоса или характеристику трубопровода. Это можно сделать различными способами, например, изменив сопротивление трубопровода или режим работы насоса. 36. Истечение жидкости через малые отверстия при постоянном напоре. Отверстия в гидравлике делятся на малые и большие. Малые – отверстия, в различных точках которого геометрический напор одинаков.  Форма отверстий во многих случаях существенно сказывается на параметрах вытекающего потока и его формы. Изменение формы стекающей струи жидкости относительно отверстия называется инверсией жидкости. Отверстия могут выполняться в тонкой или толстой стенке. Стенка считается тонкой, если её толщина S<2/3 напора. Толстая стенка, если S>2/3 напора. Явление сжатия струи через отверстие в тонкой стенке на определенном расстоянии:  - коэффициент сжатия струиСжатие называют совершенным, если боковые стенки сосуда не влияют на истечение струи. Полное – сжатие по всему периметру Если H=const, то это стечение при постоянном напоре Свободное стечение жидкости – истечение жидкости в атмосферу. Скорость и расход жидкости :   Скорость для реальной жидкости корректируется с помощью коэффициентов  - коэффициент скорости.Для расхода  - коэффициент расхода |