5. Основные уравнения гидростатики и его физический смысл

• Название: 5. Основные уравнения гидростатики и его физический смысл
• Анкор: gidra_otvety.docx
• Дата: 13.05.2017
• Размер: 9.76 Mb.
• Имя файла: gidra_otvety.docx
• Тип: Документы; #7517
• страница: 1 из 5

5. Основные уравнения гидростатики и его физический смысл

Что бы получить ОУГ нужно проинтегрировать ур-е Эйлера для жидкости находящейся в поле действия только силы тяжести.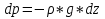


Проинтегрировав: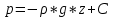



Если принять: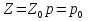



Тогда: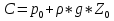



ОУГ: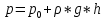



Давление в любой точке покоящейся жидкости равно давлению на поверхности + давление столба жидкости над ней.

В Другом виде ОУГ представляет собой частный случай выражения основного закона сохранения энергии (сумма потенциальной и кинетической энергии постоянная) :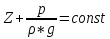



6. Закон Паскаля и его практическое применение

Внешнее давление в объеме покоящейся жидкости во все стороны передается одинаково.

Рассмотрим два сообщающихся сосуда разного диаметра сверху закрытых поршнями. К поршню меньшего диаметра приложена внешняя сила R1 . Необходимо определить какую силу R2 сможет преодолеть больший поршень, если диаметр меньшего поршня d, большего D? От приложенной внешней нагрузки R1 под меньшим поршнем возникает гидростатическое давление равное

w1 – площадь меньшего поршня равная

Так как по своим свойствам гидростатическое давление по все стороны действует одинаково и всегда перпендикулярно к поверхности, воспринимающей это давление, то под большим поршнем возникнет гидростатическое давление Р0 способное преодолеть внешнюю силу R2 = P0w2 , где

w2 – площадь большего поршня, равная

Таким образом,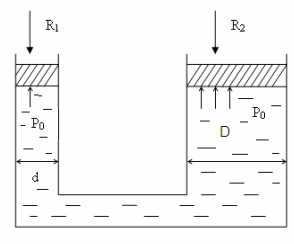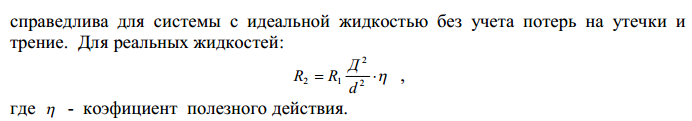

7. 
   Определение силы давления жидкости на плоские поверхности
   

7. 
   Определение силы давления жидкости на криволинейные поверхности
   

7. 
   Виды давлений, единица их измерения, соотношения между ними, приборы для измерения давления.
   

Единицей измерения давления в системе СИ служит , её называют паскаль(Па). Так как эта единица очень мала, часто применяют укрупненные единицы: килоньютон на квадратный метр и меганьютон на квадратный метр. Давление равное

В физической системе единицей давления является дина на квадратный сантиметр, в технической– килограмм– сила на квадратный сантиметр, называемая технической атмосферой. Между приведенными единицами измерения давления существуют

следующее соотношение:



Если при определении гидростатического давления учитывают и атмосферное давление, действующее на свободную поверхность жидкости, его называют полным, или абсолютным. В этом случае давление обычно измеряется в технических атмосферах, называемых абсолютными(ата). Часто при учете давления атмосферное давление свободной поверхности не принимают во внимание, определяя так называемое избыточное, или манометрическое, давление, т.е. давление сверх атмосферного. Манометрическое давление определяют как разность между абсолютным давлением в жидкости и давлением атмосферным Рман=Рабс-Рат и измеряют также в технических атмосферах, называемых в этом случае избыточными(ати). Встречаются также случаи, когда гидростатическое давление в жидкости оказывается меньше атмосферного. В таких случаях говорят, что в жидкости имеется вакуум(разрежение). Вакуум определяется разностью между атмосферным и абсолютным давлениями в жидкости Рвак=Рат-Рабс. и измеряется в пределах от нуля до одной атмосферы.

7. 
   Гидродинамика.
   

Гидродинамикой называется раздел гидравлики, в котором изучаются законы движения жидкости. Если скорость и давление в каждой точке пространства, заполненного движущейся жидкостью, остаются все время постоянными(но могут меняться при переходе из одной точки пространства к другой), движение называется установившемся. Говоря иначе, при установившемся движении поле скоростей и поле давлений с течением времени остаются неизменными. При неустановившемся же движении поле скоростей и поле давлений будут непрерывно изменяться. Установившийся режим движения делится на равномерное и неравномерное движение.

Равномерный режим движения- это режим при котором площадь живых (поперечных) сечений потока не изменяется с течением времени.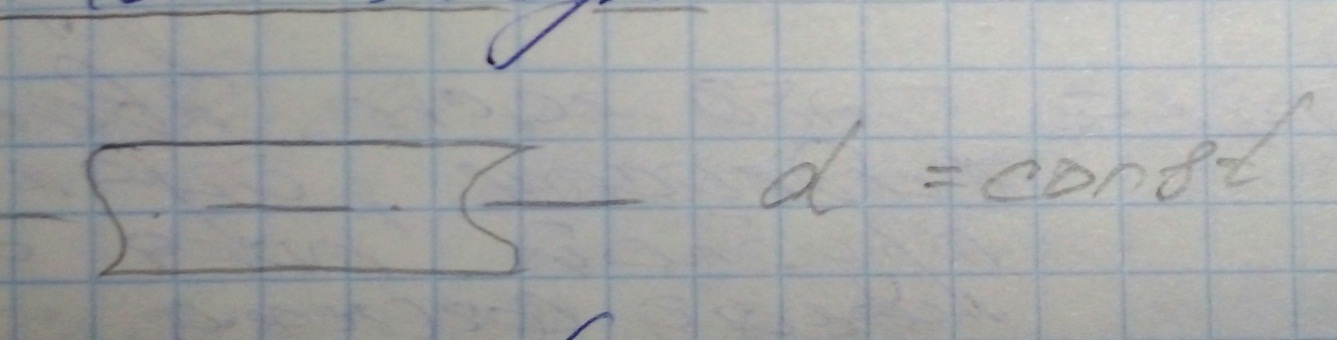



Если площадь переменна– режим неравномерный.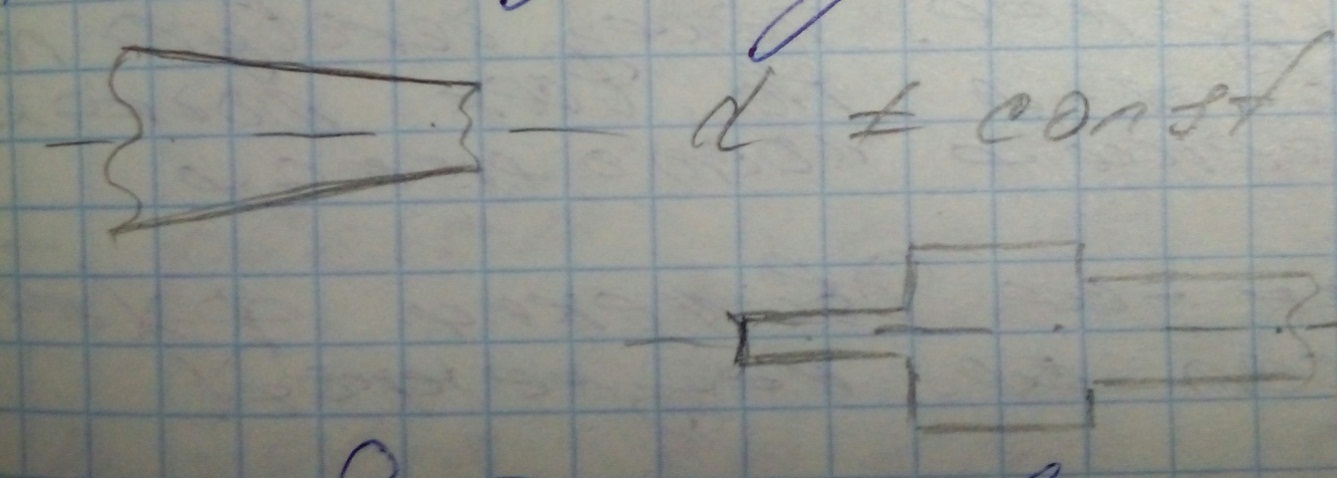

Напорный режим наблюдается в том случае, если поток жидкости заключен в твердые стенки и не имеет свободной поверхности. Если над потоком имеется свободная поверхность- режим безнапорный.

7. 
   Элементарная струйка.
   

Элементарная струйка –это часть движущейся жидкости ,ограниченная трубкой только бесконечно малого сечения.

Свойства:

- частицы жидкости не входят и не выходят из неё через боковую поверхность.

- скорость движения во всех точках поперечного сечения постоянная.

- при установившемся движении форма струйки остаётся неизменной.

7. 
   Поток жидкости и его основные характеристики.
   

Поток характеризуется следующими параметрами:

1)Живое сечение - поперечное сечение нормальное к направлению движения. Оно характеризуется площадью 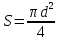, 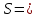bh.

2)Смоченный периметр – это след жидкости на поверхности живого сечения.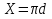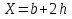

,.

3)Гидравлический радиус – отношение площади живого сечения к смоченному периметру.



4)Эквивалентный диаметр – это величина, равная 4-м гидравлическим радиусам(используется при расчётах трубопровода любого поперечного сечения)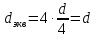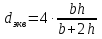





13.Расход жидкости(виды расходов) и средняя скорость. Способы их определения

Расходом называется количество жидкости, протекающей через живое сечение потока в единицу времени.

Различают:

объемный (Q) :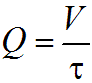



массовый (Qm) :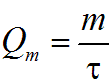



весовой (G)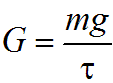



расходы жидкости. Где V— объем жидкости; m — масса жидкости; ? — время.

Объемный расход потока с живым сечением F определим с использованием понятия средней скорости потока wcp:



Средняя скорость — это условная скорость потока, которая считается одинаковой для всех частиц данного сечения, но подобрана так, что расход, определенный по ее значению, равен истинному значению расхода.

14. Уравнения неразрывности для элементарной струйки и потоки жидкости.

Если несжимаемая жидкость движется без разрывов, то при установившемся движении объемный расход для всех живых сечений потока постоянен, т.е. можно записать, что вдоль потока



Это уравнение называют уравнением неразрывности потока, оно является первым основным уравнением гидродинамики. Из него следует, что средние скорости обратно пропорциональны площадям соответствующих живых сечений потока.

14(2). Уравнение неразрывности для элементарной струйки и потока жидкости при установившемся движении. В гидравлике обычно рассматривают потоки, в которых не образуются разрывы и не заполненные жидкостью пустоты, т.е. жидкость сплошь заполняет пространство.

Рассмотрим элементарную струйку несжимаемой жидкости при установившемся движении. Выделим сечение 1-1 и 2-2, расположенные на расстоянии l одно от другого (рис.1.23). Здесь Δs1 и Δs2 - площади живых сечений соответственно; u 1 и u2 - скорости; ΔQ1 и ΔQ2 - расходы элементарной струйки в сечениях.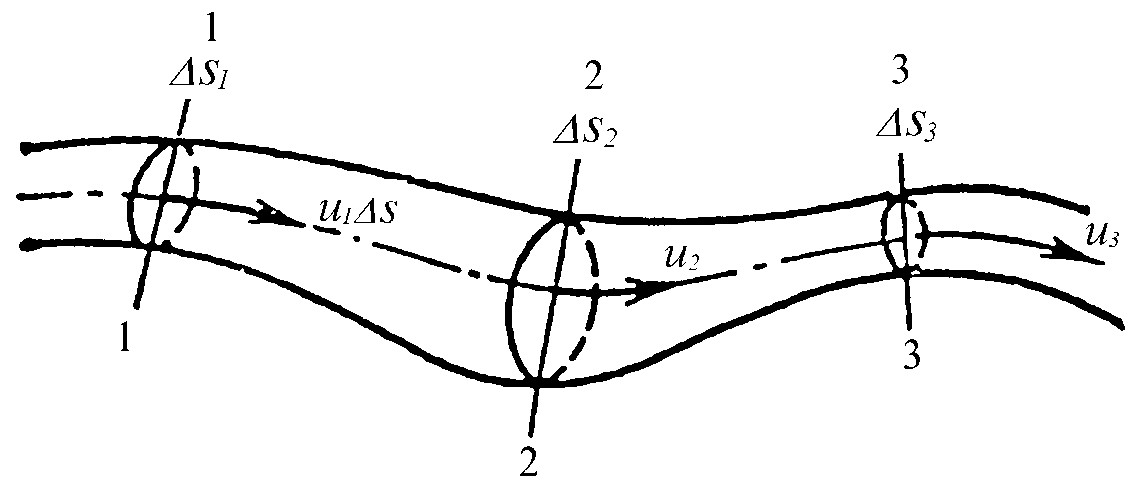



Рис. 1.23. Элементарные струйки несжимаемой жидкости при установившемся режиме движения

Очевидно, что ΔQ1 = Δs1u1 и ΔQ2 = Δs2u2, причем ΔQ1 втекает в рассматриваемый отсек, а ΔQ 2 - вытекает.

Учитывая, что форма элементарной струйки не изменяется с течением времени, поперечный приток и отток невозможен, так как скорости на боковой поверхности струйки направлены по касательным к линиям тока, из которых состоит эта боковая поверхность, получаем, что расходы ΔQ1 и ΔQ2 равны, т.е.

Δs1u 1 = Δs2u2. (1.50)

Аналогичные соотношения можно написать для любых двух сечений элементарной струйки, расположенных вдоль нее:

u1Δs1 = u2Δs2 =...= uΔs = ΔQ = const (1.51)

Это и есть уравнение неразрывности для элементарной струйки несжимаемой жидкости при установившемся движении.

Если выделить в потоке два любых сечения, отстоящих на некотором расстоянии, то, просуммировав по каждому из живых сечений обе части в уравнении (1.50)



Таким образом, в отмеченных условиях расход, проходящий через все живые сечения потока, неизменен, несмотря на то что в каждом сечении средняя скорость и площадь живого сечения могут быть различны.

Из (1.52) получим также важное соотношение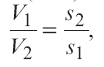



т.е. средние скорости обратно пропорциональны площадям живых сечений потока, которым соответствуют эти средние скорости.

Уравнение неразрывности (1.52) является одним из основных уравнений гидродинамики.

17. Геометрический, энергетический смысл уравнения Бернулли.

Все члены уравнения Бернулли (2.66) имеют линейную размерность, и каждый из них может называться высотой, например: z – геометрическая высота, gV22 – высота скоростного напора.

Сформулируем геометрический смысл уравнения Бернулли.

При установившемся движении жидкости элементарной струйки сумма трех высот есть величина постоянная вдоль элементарной струйки.

Уравнение Бернулли (2.68) выражает один из случаев закона сохранения энергии в любом сечении элементарной струйки.

Таким образом, энергетический смысл уравнения Бернулли заключается в следующем: при установившемся движении жидкости элементарной струйки сумма трех удельных энергий (энергии положения, энергии давления и кинетической энергии) остается неизменной вдоль элементарной струйки. В уравнении Бернулли (2.66) можно слагаемые рассматривать как удельные энергии, но уже по отношению к единице веса жидкости.
18. Дифференциальные уравнения движения реальной жидкости (уравнения Навье-Стокса).

Уравнения Навье —Стокса —система дифференциальных уравнений в частных производных, описывающая движение вязкой ньютоновской жидкости.

В случае несжимаемой жидкости система состоит из двух уравнений:

-Уравнения движения

-Уравнения неразрывности

В векторном виде для несжимаемой жидкости они записываются следующим образом:



где  — оператор набла,  — векторный оператор Лапласа,  — время,  — коэффициент кинематической вязкости,  — плотность,  — давление,  — векторное поле скоростей,  — векторное поле массовых сил. Неизвестные и являются функциями времени .
19. Уравнения Д. Бернулли для потока реальной жидкости.

В реальных потоках жидкости присутствуют силы вязкого трения. В результате слои жидкости трутся друг об друга в процессе движения. На это трение затрачивается часть энергии потока. По этой причине в процессе движения неизбежны потери энергии. Эта энергия, как и при любом трении, преобразуется в тепловую энергию. Из-за этих потерь энергия потока жидкости по длине потока, и в его направлении постоянно уменьшается. Т.е. напор потока Hпотока в направлении движения потока становится меньше. Если рассмотреть два соседних сечения 1-1 и 2-2, то потери гидродинамического напора” h составят:

,

где H1-1- напор в первом сечении потока жидкости,

H2-2- напор во втором сечении потока,

h - потерянный напор - энергия, потерянная каждой единицей веса движущейся жидкости на преодоление сопротивлений на пути потока от сечения 1-1 до сечения 2-2.

С учётом потерь энергии уравнение Бернулли для потока реальной жидкости будет выглядеть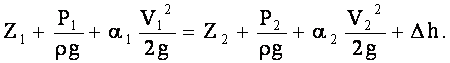



20. Коэффициент «альфа» в уравнении Д. Бернулли и его физический смысл.

Коэффициент Кориолиса. Для применения уравнения Бернулли необходимо знать величину удельной энергии.

Коэффициент Кориолиса при турбулентном режиме течения меняется в пределах от 1,11 до 1,15.

Коэффициент Кориолиса а является определенной величиной и характеризует степень неравномерности распределения скоростей по живому сечению потока. Установлено, что а> I и обычно его значение заключено в пределах а =1,03-=- 1,1. В инженерной практике чаще всего принимают а=1.

Обычно коэффициент Кориолиса определяется опытным путем. Он зависит от степени неравномерности распределения скоростей в поперечном сечении потока и всегда больше единицы; для так называемого ламинарного режима в цилиндрической трубе а = 2, а для так называемого турбулентного режима а = = 1,0454-1,10.
21. Графическое представление и практическое применение Д.Бернулли

Выделим двумя нормальными к линиям тока сечениями 1 - 1 и 2 - 2 отсек жидкости, который будет находиться под действием сил давленияи сил тяжести dGПод действием этих сил через малый промежуток времени отсек жидкости из своего первоначального положения переместится в положение между __сечениями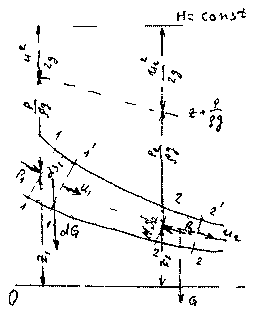



Силы давления, приложенные к живым сечениям отсека с правой и с левой сторон имеют противоположные друг другу направления.

Перемещение всего отсека жидкости можно заменить перемещением массы жидкости между сечениями: 1-1иГ-Г в положение 2-2и2'-2', при этом центральная часть отсека жидкости (можно утверждать) своего первоначального положения не меняет и в движении жидкости участия не принимает.

Тогда работа сил давления по перемещению жидкостиможно определить следующим образом: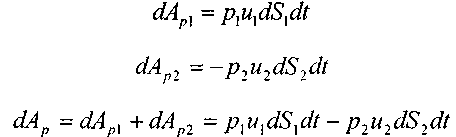

Работа сил тяжести будет равна работе по перемещению веса отсека жидкости на разницу уровней

При перемещении отсека жидкости кинетическая энергия изменится на величину:

f

Теперь запишем общее уравнение баланса энергии:



Разделив все элементы уравнения на dGи, переместив в левую часть уравнения величины с индексами «1» а в правую - с индексом «2», получим:



Это последнее уравнения носит название уравнения Бернулли для элементарной струйки идеальной жидкости.

Интерпретация уравнения Бернулли

Все члены уравнения Бернулли имеют линейную размерность и представляют собой напоры:

z - называется геометрическим напором (геометрической высотой), представляет собой место положения центра тяжести живого сечения элементарной струйки относительно плоскости сравнения,

- называется пьезометрическим напором (пьезометрической высотой),

представляет собой высоту, на которую могла бы подняться жидкость при отсутствии движения

- носит название скоростного напора.

- носит название гидродинамического напора

Уравнение Бернулли является выражением закона сохранения механической энергии движущейся жидкости, по этой причине все части уравнения представляют собой величины удельной энергии жидкости:

z - удельная энергия положения,

- удельная энергия давления,

- удельная потенциальная энергия,

- удельная кинетическая энергия

- удельная механическая энергия.