5. Основные уравнения гидростатики и его физический смысл

• Название: 5. Основные уравнения гидростатики и его физический смысл
• Анкор: gidra_otvety.docx
• Дата: 13.05.2017
• Размер: 9.76 Mb.
• Имя файла: gidra_otvety.docx
• Тип: Документы; #7517
• страница: 2 из 5

22. Режимы движения жидкости. Опыт О.Рейнольдса и его анализ

Ламинарный – жидкость движется слоями, не перемешиваясь; при малых скоростях струйка не перемешивается с др. жидкостью.

Турбулентный – частицы жидкости перемешиваются; при больших скоростях струйка перемешивается со всей жидкостью , что указывает на наличие турбулентного течения.

В 1885г. Рейнольдсом было установлено, что критерием режима жидкости является безразмерная величина представляющая собой: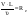
этот критерий режима течения называется числом Рейнольдса.
При напорном движении жидкости в круглых за характерный размер L принимают диаметр трубы, в остальных случаях гидравлический радиус.

Опытно доказано, что ламинарный режим устойчив, если отношение: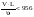
если же больше 956, то неустойчив. Пользуясь числом Рейнольдса моно заранее установить какой режим течения будет в патоке.

Режимы течения жидкости

Расчетное выражение для А._г (и численное значение коэффициента) зависит от режима теченияжидкости. Понятие о режимах течения утвердилось в гидравлике после исследований английского ученого О.Рейнольдса в конце XIX в.

Экспериментальная установка Рейнольдса состояла (рис.) из прозрачного резервуара 1, заполняемого рабочей жидкостью (уровень ее в ходе опыта поддерживался постоянным с помощью подпитки 7 и сливного устройства 4),прозрачной горизонтальной трубы 2с плавным входом, регулировочного вентиля3и сосуда с жидкой темной краской 6.Из сосуда 6краска по капиллярной трубке могла подводиться в какую-либо точку входного сечения трубы 2(поток краски регулировали краном 5). В ходе опытов варьировали диаметр труб 2,скорости жидкости (их рассчитывали по расходу) и ее свойства (плотность, вязкость). Индикатором характера течения служила краска.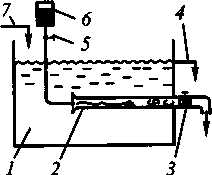

 

Опыт Рейнольдса:

1 —резервуар с рабочей жидкостью, 2 —экспериментальная труба, 3 —регулирующий вентиль, 4 —слив избытка жидкости, 5 — кран, 6 —сосуд с краской, 7 — линия подачи рабочей жидкости

Опыты с гладкими трубами показали, что в трубах малого диаметра при небольших скоростях жидкости подаваемая во входное сечение струйка краски проходила по всей длине трубы не размываясь. Такое параллельно-струйчатое (слоистое) течение было названо ламинарным(по латыни lamina — полоска, пластинка). В трубах большого диаметра и при высоких скоростях частицы жидкости (а с нею и краски) перемещались хаотически по различным траекториям — с визуально наблюдаемыми завихрениями; в результате поток интенсивно перемешивался и на некотором расстоянии от входа в трубу равномерно окрашивался. Такое бурное течение с нестационарным возникновением и разрушением жидкостных образований было названо турбулентным(turbulentus означает бурный, беспорядочный). Рейнольдc установил, что склонность жидкости к ламинарному течению возрастает при увеличении ее вязкости и понижении плотности р, к турбулентному течению — с ростом р и снижением µ. Позднее было найдено, что характер течения определяется значением безразмерного комплекса

wdp/µ=wd/v=Re,

w - скорость движения жидкости,

d - внутренний диаметр трубы,

v,µ- кинематическая и динамическая вязкость. 

названного впоследствии числом Рейнольдса. При значениях Rе ниже некоторой критической величины (Rе _кр) течение жидкости — ламинарное; для круглых труб Rе _кр примерно равно 2300. При увеличении Rе (для изотермического течения в прямых круглых трубках — сверх 10⁴) течение становится существенно турбулентным, причем с ростом Rе интенсивность турбулентности повышается.

Rе представляет собой соотношение сил инерции и вязкости. В случае ламинарного режима (малые значения Rе) доминируют силы вязкости (они — в знаменателе Rе), влияние сил инерции вырождается. При этом использование числа Rе, вообще говоря, теряет смысл (или приобретает формальный характер). В случае турбулентного режима (высокие Rе) в целом преобладают силы инерции. Однако вблизи стенок канала (в очень тонком слое), где скорости малы, течение остается близким к ламинарному; поэтому силы вязкости продолжают оказывать некоторое влияние на характер течения — использование Rе для характеристики таких течений сохраняет смысл. Лишь при очень высоких Rе (для круглых труб — свыше 2*10⁷) пристенный слой оказывается практически сорванным — доминируют силы инерции, а влияние сил вязкости вырождается. Значит, вырождается и число Rе — его использование становится формальным. В обоих случаях доминирования сил вязкости либо инерции течения именуют автомодельнымиотносительно критерия Рейнольдса . При значениях Rе, несколько превышающих Rе _кр (от 2300 до 10000), силы инерции и вязкости сопоставимы по величине: здесь уже нарушено слоистое течение, но неупорядоченность (хаотичность) выражена еще слабо. Эти режимы течения называются переходными(в зарубежной литературе — промежуточными).

На практике возможно некоторое смещение указанных диапазонов. Так, при очень плавном входе жидкости в круглую трубу и отсутствии каких-либо внешних возмущений удается сохранить ламинарный режим при Rе, заметно превышающих 2300. Наоборот, при неблагоприятных условиях входа (наличии вибрации, турбулизующих вставок, шероховатости стенок канала) течение становится турбулентным при Rе значительно ниже 10⁴.

Особенно сильное влияние внешние условия оказывают на течение в переходном режиме — его характеристики могут смещаться в сторону ламинарного либо турбулентного. В этом смысле переходный режим плохо воспроизводится, так что расчетные формулы для различных эффектов переноса в переходном режиме (не только в гидравлике, в тепло- и массообменных процессах — тоже) обычно весьма ненадежны и пригодны лишь для определения качественных связей между различными факторами и приближенной оценки численных значений характеристик процесса.

Физические предпосылки возникновения и поддержания ламинарного или турбулентного режима можно представить следующим образом. В жидкостном потоке под влиянием постоянно действующих случайных возмущений непрерывно возникают отклоненияот характерных (для данного течения) параметров движения жидкости. Но при доминировании сил вязкостиупомянутые отклонения подавляются,и движение остается упорядоченным, т.е. ламинарным.Этого не происходит, когда преобладают силы инерции:возникшие возмущения здесь развиваются, распространяются по объему потока движение становится неупорядоченным, т.е. турбулентным.

Переход к неупорядоченному течению стимулируется внешними (по отношению к потоку жидкости) причинами: преградами в канале, шероховатостью его стенок, вибрацией каналов и т.п.
23. Основы теории гидродинамического подобия. Виды подобия и основные критерии.

Геометрическоеподобие, как известно из геометрии, предполагает пропорциональность сходственных размеров и равенство соответствующих углов. В гидравлике под геометрическим подобием понимается подобие тех поверхностей, которые ограничивают потоки, то есть подобие русел или каналов. При этом подобными должны быть не только русла в пределах изучаемого участка, но и непосредственноперед и за ними, так как они будут оказывать влияние на характер течения жидкости на изучаемом участке. Отношение двух сходственных размеров подобных русел назовем линейным масштабом и обозначим черезkL. Эта величина одинакова (idem) для подобных русел I и II: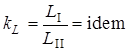

.

Кинематическоеподобие означает пропорциональность местных скоростей в сходственных точках и равенство углов, характеризующих направление этих скоростей: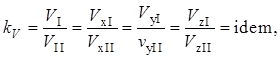



где kV – масштаб скоростей, одинаковый при кинематическом подобии.

Так как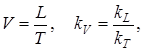



где T –время, kT – масштаб времени.

Очевидно, что для кинематического подобия необходимо геометрическое подобие русел.

Динамическоеподобие– это пропорциональность сил, действующих на сходственные объемы в кинематически подобных потоках и равенство углов, характеризующих направление этих сил.

В потоках жидкости обычно действуют разные силы: силы давления, вязкости, тяжести и др. Соблюдение этих пропорциональностей означает полное гидродинамическое подобие. Осуществить полное подобие на практике удается далеко не всегда, поэтому часто имеют дело с частичным (неполным) подобием, при котором пропорциональны только лишь основные, главные силы.

Для напорных течений в закрытых руслах, то есть для потоков в трубах, в гидромашинах и т. п., такими силами являются силы давления, вязкости и инерции. На жидкость действует также сила тяжести, но в напорных потоках ее действие проявляется через давление: pпр = p + grh, то есть она учитывается.

Силы инерции определяются произведением массы на ускорение F = ma, а их отношение в подобных потоках равно масштабу сил: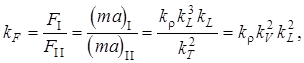



где kr – масштаб плотностей.

Таким образом, силы инерции пропорциональны плотности, квадрату скорости и размеру L во второй степени, то есть площади S:



Силы инерции примем за основу и другие силы будем сравнивать с инерционными, то есть с 

Таким образом, для гидродинамического подобия потоков необходимо, чтобы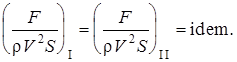



Это отношение называют числомНьютона и обозначают Ne.

24.Основы теории ламинарного движения(распределение касательных напряжения и скоростей, определение потерь напора)

Ламинарное движение является строго упорядоченным, слоистым течением без перемешивания жидкости.

Рис. 1.6.1. Слоистый характер потока при ламинарном течении жидкости

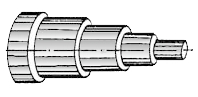
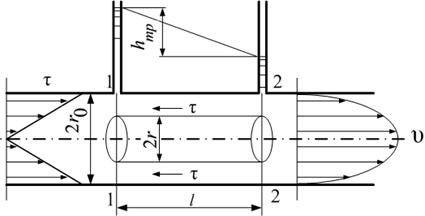
Так как в этом случае перемещение частиц жидкости происходит только в осевом направлении, а поперечные составляющие скорости отсутствуют, то схематически ламинарный поток можно представить в виде бесконечно большого числа бесконечно тонких, концентрично расположенных цилиндрических слоев, параллельных оси трубопровода и движущихся один внутри другого с различными скоростями, увеличивающимися в направлении от стенок к оси трубы (рис. 1.6.1).

Слои жидкости, движущиеся быстрее, увлекают за собой слои, движущиеся медленнее, и наоборот, слои, движущиеся медленнее, тормозят слои жидкости, движущиеся быстрее. Происходит как бы скольжение цилиндрического слоя, движущегося с большей скоростью, по слою, движущемуся с меньшей скоростью. При этом из-за наличия сцепления частиц жидкости друг с другом и со стенками трубы на соприкасающихся поверхностях слоев жидкости возникают силы трения, направленные параллельно оси трубы, навстречу потоку.

1.6.1 Распределение скоростей и касательных напряжений по сечению круглой трубы

Рассмотрим установившееся ламинарное течение жидкости в прямой круглой цилиндрической трубе с внутренним диаметром . Чтобы исключить влияние силы тяжести и этим упростить вывод уравнений, расположим трубу горизонтально. Достаточно далеко от входа в нее, где поток уже вполне сформировался, выделим участок длиной  между сечениями 1-1 и 2-2 (рис. 1.6.2).

Рис. 1.6.2. Распределение скоростей и касательных напряжений по сечению круглой трубы

Пусть в сечении 1-1 давление равно , а в сечении 2-2 - . В цилиндрической трубе скорость жидкости будет постоянной, а коэффициент  будет неизменным вдоль стабильного потока, тогда уравнение Бернулли для выбранных сечений примет вид (1.4.10)

,

где  - потеря давления на трение по длине трубы, определяемая по показаниям пьезометров, установленных в этих сечениях (см. рис. 1.6.2).

В потоке жидкости выделим цилиндрический объем радиусом , соосный с трубой и имеющий основания в выбранных сечениях. Запишем уравнение равномерного движения выделенного объема жидкости в трубе, которое представляет собой равенство нулю суммы сил давления и сопротивления, действующих на объем,



откуда

,                                       (1.6.1)

где  - касательное напряжение на боковой поверхности выделенного цилиндра.

Из формулы (1.6.1) следует, что касательные напряжения в поперечном сечении трубы изменяются по линейному закону в зависимости от радиуса. На оси трубы , так как . На стенке трубы, где , касательные напряжения достигают максимального значения.

Эпюра касательного напряжения показана на рис. 1.6.2 слева.

Касательное напряжение  по закону трения Ньютона можно выразить через динамическую вязкость и поперечный градиент скорости (1.1.12), а если при этом заменить  (расстояние от стенки трубы) текущим радиусом, то получим

.                            (1.6.2)

Знак минус обусловлен тем, что направление отсчета  (от оси трубы к стенке) противоположно направленно отсчета  (от стенки).

Приравняв правые части уравнений (1.6.1) и (1.6.2), получим

,

откуда приращение скорости

.                                (1.6.3)

При положительном приращении радиуса получается отрицательное приращение (уменьшение) скорости, что соответствует профилю скоростей, показанному на рис. 1.6.2.

Выполнив интегрирование выражения (1.6.3) для условия, что на стенке трубы при , получим закон распределения скоростей по сечению круглой трубы при ламинарном движении жидкости

.                               (1.6.4)

Максимальная скорость на оси трубы (при условии, что )

,                                 (1.6.5)

а кривая, изображающая эпюру скорости (рис. 1.6.2 справа), является параболой второй степени.

Элементарный расход  жидкости через бесконечно малую площадку 

.

Если  представить в виде функции радиуса  (1.6.4), а площадку  - в виде кольца радиусом  и шириной , то

.

После интегрирования по всей площади поперечного сечения, то есть от  до , получим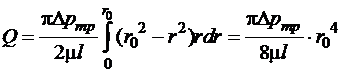

.               (1.6.6)

Среднюю по сечению скорость жидкости найдем делением расхода на площадь. С учетом выражения (1.6.6) получим

.                        (1.6.7)

Сравнение полученного выражения с формулой (1.6.5) показывает, что средняя скорость при ламинарном движении в два раза меньше максимальной: .

Из этого следует, что коэффициент Кориолиса , учитывающий неравномерность распределения скоростей по сечению в уравнении Бернулли (1.4.9), для случая установившегося ламинарного движения жидкости в круглой трубе, равен двум.

Следовательно, действительная кинетическая энергия ламинарного потока с параболическим распределением скоростей по сечению в два раза превышает кинетическую энергию того же потока, но при равномерном распределении скоростей.