5 Тарихи есептер Египет есептері 70 гіз айдап бара жатан баташыдан былай деп сраан гіз табыны анша блігін айдап бара жатырсы

• Название: 5 Тарихи есептер Египет есептері 70 гіз айдап бара жатан баташыдан былай деп сраан гіз табыны анша блігін айдап бара жатырсы
• Дата: 08.11.2021
• Размер: 0.89 Mb.
• Имя файла: 0005eeeb-378d5bf9.doc
• Тип: Документы; #265759
• страница: 2 из 6

Абу Али – Ибн – Сина (Авиценна) (980-18.06.1037)

1. Егер санды 9-ға бөлгенде қалдығы 1 немесе 8 болса, онда бұл санның квадратын 9-ға бөлгенде қалдығы 4 болады.

Егер санды 9-ға бөлгенде қалдығы 2 не 7 болса, онда бұл санның квадратын 9-ға бөлгенде қалдығы 4 болады.

Егер санды 9-ға бөлгенде қалдықтары 1, 4 не 7 болса, онда ол санның кубын 9-ға бөлгенде қалдығы 1 болады.

Абу Бахр Мухамед ибн Ал – Хасан Ал – Караджи (X-XIст)

1. т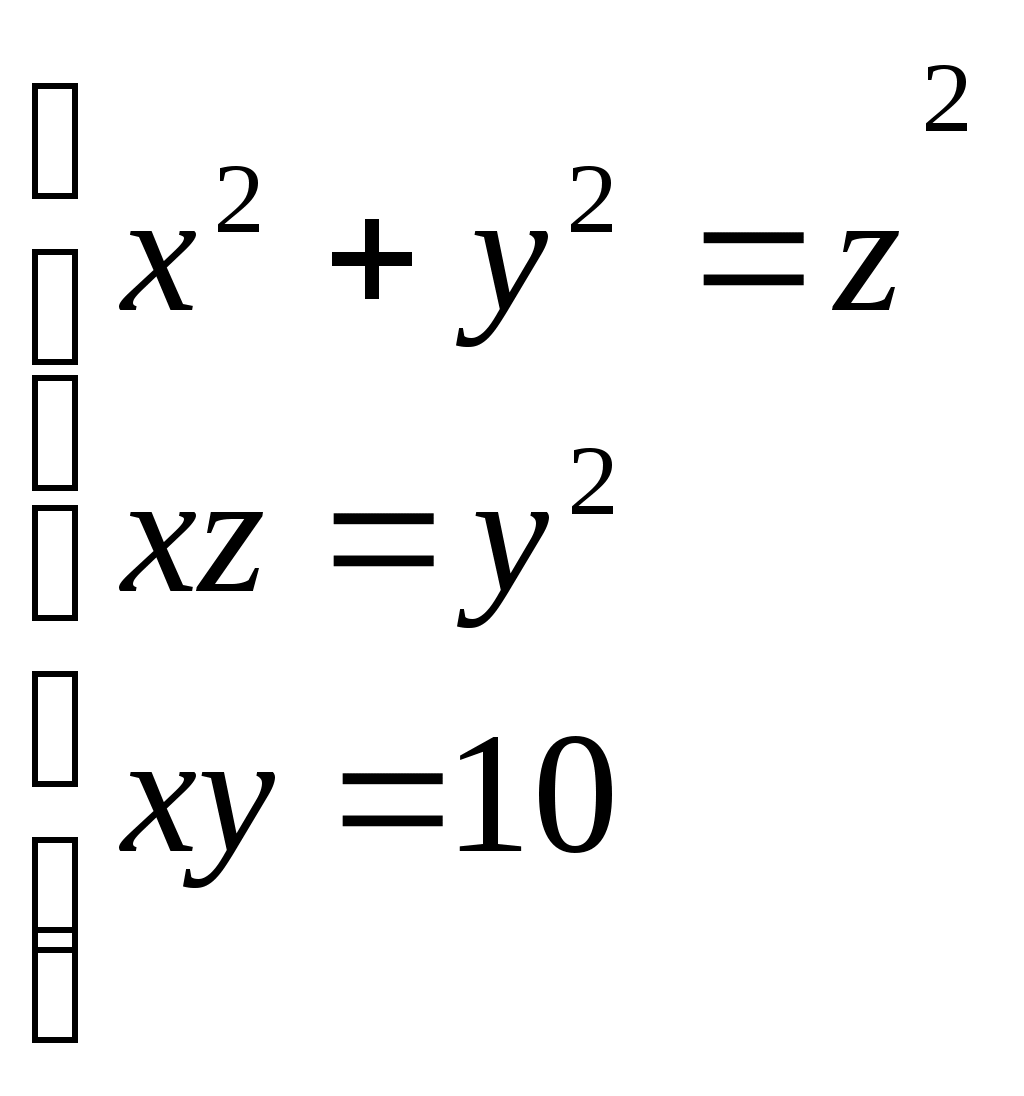еңдеуін шеш.

2. теңдеулер жүйесін шеш.

3. теңдеуін шеш.

Джемшид Ибн-Мамуд-Каши ( 1430ж өл)

1. Бақшада бірінші адам – бір анар ( гранат), екінші адам екі анар, ал келесілері олардан бір анарға артық жұлып алады. Одан кейін анар жинағандар өзара тең бөлісіп алғанда әрбіреуіне алты анардан келген. Қанша адам анар жинайды?

2. Екі жаяу адам бір уақытта дөңгелек көлдің жағасынан бір нүктеден қарама- қарсы бағытта шықты. Біріншісі күніне 10 мильден жүрді, ал екіншісі бір күнде 1 миль, ал қалған әрбір келесі күнде 1 мильге артық жүрді. Екеуі кездескенде біріншісі шеңбердің -ін, ал екіншісі -ін жүріп өткені белгілі болды. Көлдің жағасының ұзындығы қанша және жаяулар жолда қанша уақыт болды?

3. Онды бірінші бөлігінің квадраты мен екінші бөлігінің қосындысы дәл квадрат болатын екі санға бөлу керек.

4. Егер санға -ді қосса немесе азайтса, онда пайда болған қосынды мен азайтынды дәл квадраттар болады. Сол санды табу керек.

5. Суда вертикаль тұрған таяқша судан үш шынтақ шығып тұрды. Жел соққанда таяқ төбесі су бетінде, ал табаны өз орнында қалып көлбеді. Егер таяқтың төбесінің бастапқы орны мен су бетіндегі оның ара қашықтығы бес шынтақ болса, таяқтың ұзындығын табу керек.

Жауабы:

Ал-Хорезми-Абу-Абдаллах-Мұхамед ибн Мұса (783-850ж)

1. Теңдеулердің алты түрі: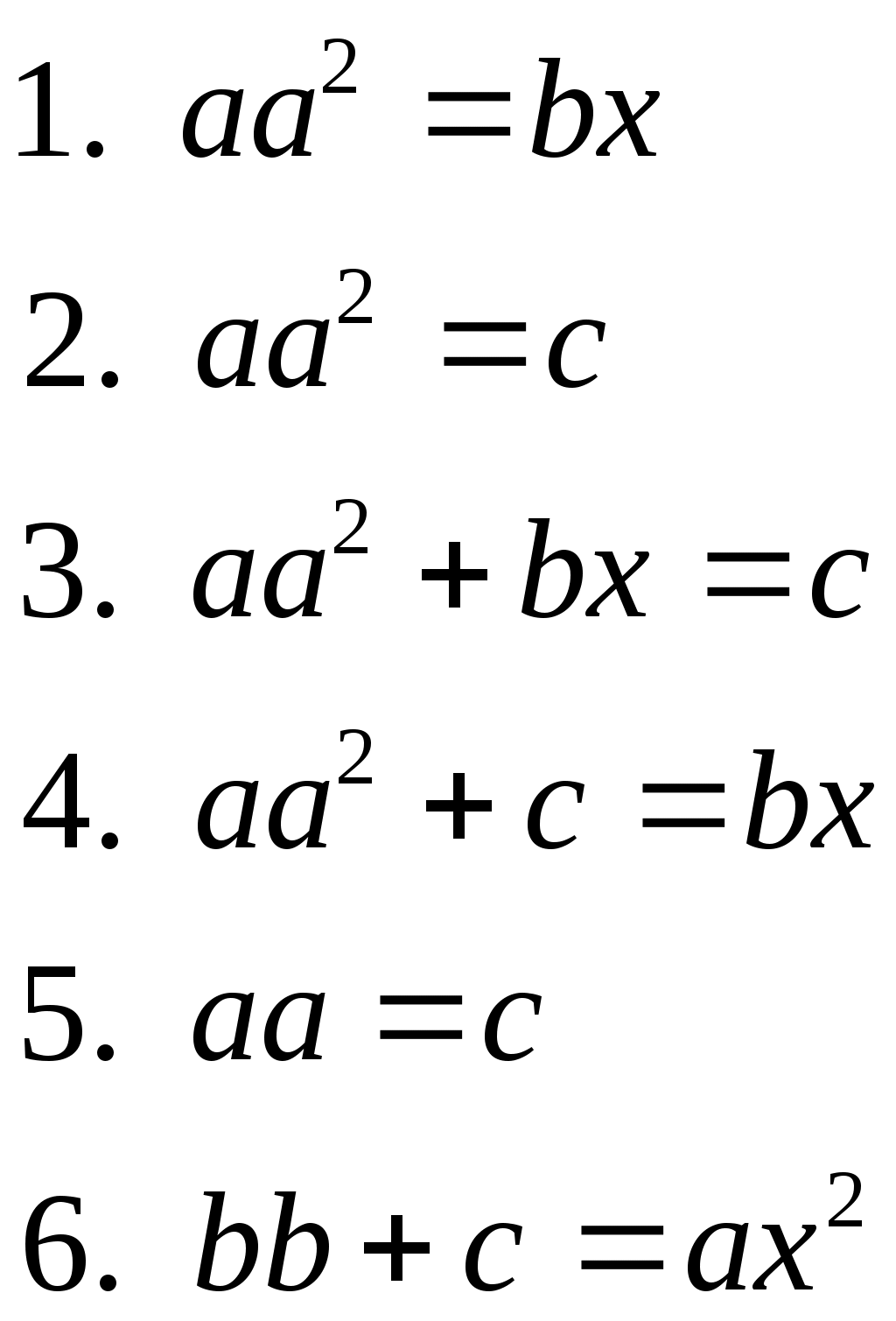



2. Кез келген тікбұрышты үшбұрыштың әрбір қысқа қабырғасын өзіне көбейтсе, онда көбейтінділердің қосындысы үлкен қабырғасының өз-өзіне көбейтіндісіне тең.

3. Егер дөңгелектің диаметрін өзіне көбейтіп, одан диаметрінің бөлігін, және осы бөліктің жартысын алып тастаса, оның ауданы шығады.

Орта ғасырдағы Европа.

Алкуни (735-804)

1. Ит өзінен 150 фут қашықтықтағы қоянды қуып келеді, және ит әрбір секіргенде 9 фут, ал қоян 7 фут қашықтықты алады. Ит қоянды қуып жету үшін неше рет секіреді?

2. 100 өлшем астықты 10 адамға әрбір ер адамға 3 өлшем, әйел адамға 2 өлшем, ал балаларға ½ өлшемнен берілген. Сонда қанша ер адам, әйел адам және балалар бар?

3. Бір адам базардан 30 монетаға 30 құс сатып алды. 3 торғайға 1 монета, ал 2 тауыққа да 1 монета және әрбір көгершінге 2 монетадан төлеген. Әрбір түрінен қанша құс сатып алынды?

4. Егер бір қояндар жұбы әрбір ай сайын 1 қояндар жұбын туса және әрбір туған жұп бір айдан кейін туатын болса, онда 1 жылда ешқандай қоян өлмейді деп есептеп, қанша қоян болады?

5. Егер 0,1,1,2,3,5,8,13,21,...6 Фибоначчи тізбегі берілсе, мұндағы және борлса, онда .

6. Квадраты өзіне тең болатын санның -ға тең болатын санды тап.

7. Теңдеуді шеш:

а)

б)

с)

8. Үш адамның қандай да бір мөлшерде ақшасы бар. Біріншісінің ақшасы барлық ақшаның жартысын, екіншісінің үштен бірін, ал үшіншісінікі алтыдан бірін құрайды. Ақшалардың бір бөлігін сақтау үшін әрбіреуі ақшадан мүмкіндігінше алады. Одан кейін біріншісі сақтауға алғанының жартысын, екіншісі- үштен бірін, үшіншісі алтыдан бірін береді.Кейбір уақыттан кейін олар сол ақшаларды алады, сонда әрбіреуінде сақталған барлық ақшаның 1/3-ін құрайды.Әрбіреуінде қанша ақшадан болады?

9. 0осындылары дәл квадрат болатындай сандарын тап.
Николь Орем (1323-1382

1. теңдігін дәлелдеңіз.

2. гармониялық қатарының жинақтылығын дәлелде.

3. Шексіз үшбұрыштар жиынынан құралған фигураның ауданын табу керек, егер тіктөртбұрыштың көлденең орналасқан қабырғаларының ұзындығы 4:1 қатынасында азайтса, ал тік қабырғаларының ұзындығы 1:2 қатынасында көбейтсе.

Лука Пачоли ( 1445-1514)

4. Теңдеуді элементар тәсілмен шығар:



5. Рационал бөлшек түріне келтір.



6. Үшбұрышқа іштей сызылған дөңгелектің радиусы 4 сызықтық бірлікке тең. Жанасу нүктесі үшбұрыштың бір қабырғасын ұзындықтары 6 және 8 бірлік болатын бөлшектерге бөледі. Үшбұрыштың басқа екі қабырғасын табыңыз.

Леонардо да-Винчи (1452-1519)

1. Егер екі конгруэнтті шеңберлер қилысса, онда қиылысу нүктелері арқылы өтетін түзу шеңбердің центрінен бірдей қашықтықта жатқан нүктелер жиыны болып табылады.

Меохаэль Штифель (1486-1567)

2. Теңсіздікті тексеріңіз.



3. Теңдеуді шешіңіз.



Бұл математика тарихындағы бірінші оң жағында нолі бар теңдеудің мысалы.

НиколоТарталья (1500-1557)

1. берілген кесіндіде сызғыш пен циркуль көмегімен, тең үшбұрышты тұрғызыңыз. тең емес.

2. Біреуде 24 фунт қымбат май бар. Ол адамды сонымен қатар сыйымдылығы 13,11 және 5 фунт болатын ыдыс бар. Осы ыдыстарды қолданып майды қалайша тең үш бөлікке бөлуге болады?
Джиралома Кардало (1501-1576)

1. Теңдеуді элементар тәсілмен шығар:



Рафаэль Бомбелли(1526-1573)

1. Мынаны дәлелдеу керек:



2. Теңдеуді шешіңіз:



3. Өрнекті ықшамдаңыз: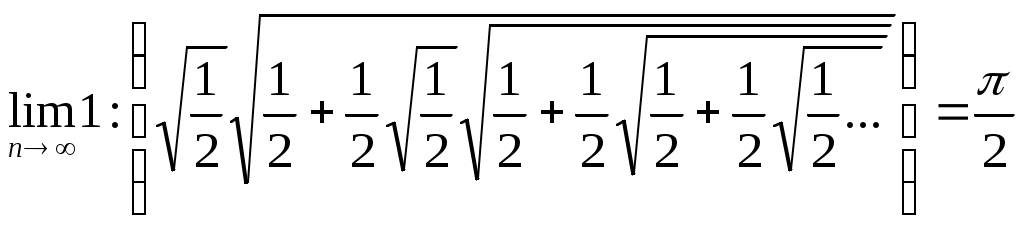



үшін Виет формуласын дәлелдеңіз.



4. Егер үшмүшелі теңдеу берілсе

,

Онда осы теңдеудің түбірлері болады, мына теңдеу үшін тексеріңіз.



5. Теңдеуді шешіңіз:



Жаңа дәуірдегі Европа.

Йоганн Кеплер (27.ХІІ.1571-15.ХІ.1630)

1. Теңдеуді шешіңіз:



Гаспар Клоуд Баше де Медриан (9.Х.1587-25.ІІ.1638)

1. Солдаттар ротасы өзеннің екінші жағына өту керек, бірақ көпір сынған ал брод жоқ. Өзен жағасында екі бала челн ойнап жүр екен. Бұл челнға бір үлкен адам немесе екі кішкентай бала сыяды. Осы челнның көмегімен рота екінші жағаға қалай өтеді?

2. Бір цифрдан тұратын төрт сан ойлаңыз. Бірінші санды екіге көбейтіп, бес қоыңыз. Қосындыны беске көбейтіп, онды және екінші санды қосыңыз.Шыққан қосындыны онға көбейтіп, төртінші санды қосыңыз да шыққан нәтижеден 3500-ді алыңыз. Сонда айырма ойланған сандармен жазылған төрт орынды сан болады.

Рене Декарт (31.ІІІ.1596-11.ІІ.1650)

1. Теңдеуді шешіңіз:

а)

б)

Пьер Ферма (1601-12.І1.1665)

1. Егер S- шексіз кемімелі геометриялық прогрессияның қосындысы болса, онда

2. АВС сүйір бұрышты үшбұрышында оның А,В және С төбелеріне дейінгі қашықтықтарының қосындысы минималь болатындай Р нүктесін табыңыз. Осы Р нүктесі Ферма-Торчелли нүктесі деп аталады.

3. үшін мына теңдік орындалады:


Джон Валлис (23. ХІ.1616-28.Х.1703).

1. белгілі, сондықтан Бұдан немесе

Блез Паскаль (19.ҮІ.1623-19.ҮІІІ.1662)

1. 
   Паскаль үшбұрышының әрбір жолдағы сандар қатарының қосындысын табу керек.
   
2. 
   Егер жұп орындағы сандарды минус таңбасымен алсақ, бұл қосынды нешеге тең болады.
   

3. 1,3,6,10,15,21;1,410,20,35,...т.с.с Паскал үшбұрышының сан қатарларын даңғыл делік. n даңғылындағы m мүшелерінің қосындысын қалай табады?

4. Паскаль үшбұрышындағы Фибонначчи сандар қатарын табу керек, яғни түріндегі (үшбұрышты) қатарды, түріндегі (пирамидальды) қатарды.
5.Кавалер де Мере сүйек ойынымен баюды көздеді. Ол ойын сүйегін 4 рет лақтырғанда ең болмағанда 1 рет 6 саны көрінеді деді. Егер олай болмаса
(6саны 4 рет лақтырғанда көрінбесе),оның қарсыласы жеңеді. Көзі жету үшін ол Паскальға жеңу ықтималдығын есептетті. Ықтималдық нешеге тең болды?
6.Екі бірдей ойыншы тең болатын жағдай жоқ ойын ойнайды. Олар тең ставка жасап, егер кім де кім 10 партияны бұрын жеңіп алса, сол жеңеді деп келісті, яғни барлық ақшаны алады деді. Ойын 9:8 есебімен аяқталады да, ойын жалғаспады. Олар ақшаны қалайша бөліп алды?
7.Барлық циркульмен орындалатын сызулар /ч/ =1 болатын шеңбер арқылы жүргізіледі.

(0,/0А/)шеңберін (мұнд /0А/=ч) және оған с нүктесінде жанама жүргіземіз. С нүктесі арқылы шеңбер Д нүктесінде қиятын доға саламыз.
Жан Озанам (1640-3.04.1717)

1. Жеті достар түскі тамақтануға жиналды, бірақ олар кім-кіммен отыру керек екендігін шеше алмады. Сол кезде біреуі оларға қалай болса да отыруды бұйырды, бірақ, келесі күні және тағы да басқа тамақтану кездерінде әртүрліше отырамыз деп келісілді. Осылайша барлық мүмкін жағдайлар аяқталғанша олар қанша рет бірге тамақтана алады?
Исаак Ньютон (4.01.1643 – 31.03.1727)

2. Бірдей қалыңдықтарда шөп өскен үш көгалдардың аудандары және 24 га. Бірінші көгалда 12 өгіз 4 күн, ал екіншісінде 24 өгіз 9 күн шамасында жайылады. Үшінші көгалдағы барлық шөпті 18 күнде жеп тауысу үшін қанша өгіз жіберуге болады?

3. Ара қашықтықтары 59 миль болатын екі жерден А және В пошташылары бір-біріне қарама-қарсы шықты. А поштасы 2 сағатта 7 миль, ал В А поштасынан 1 сағатқа кеш шығып, 3 сағатта 8 миль жүреді. А пошташысы В мен кездесу үшін қанша миль жүрді?
Тогфрид Вильгельм Лейбниц (1.07.1646 – 14.11.1716)

1. Лейбництің белгілі қатарынан үшін қатар алыңыз.

2. Дәлелдеңіз:

3. Лейбництің сандардан тұратын гормониялық үшбұрышының Паскаль үшбұрышы сияқты бірнеше қасиеттері бар.











Джованни Чева (1648 – 13.12.1734)

1. (X, Y, Z – үш нүкте берілген болсын).

АВС үшбұрышының қабырғасында жататын X, Y, Z – үш нүкте берілген болсын. (АX), (ВС), (CZ) бір нүктеде қиылысу үшін болуы қажетті және жеткілікті.

Гвидо Гранди (IX 1671 – 4.VII 1742)

1. болса, онда немесе болады. Бұдан шығатындай мүше қатарын группалау керек. Сондықтан . Бұдан