5 Тарихи есептер Египет есептері 70 гіз айдап бара жатан баташыдан былай деп сраан гіз табыны анша блігін айдап бара жатырсы

• Название: 5 Тарихи есептер Египет есептері 70 гіз айдап бара жатан баташыдан былай деп сраан гіз табыны анша блігін айдап бара жатырсы
• Дата: 08.11.2021
• Размер: 0.89 Mb.
• Имя файла: 0005eeeb-378d5bf9.doc
• Тип: Документы; #265759
• страница: 3 из 6

Лоран Патенот (1660 -01.08.1782).

1. және бұрыштары арқылы көрінетін немесе А,В,С үш нүктелері арқылы құралған және кесіндісінің нүктесін тап.
Жорж Аум-Леклерк Бюфан (7.IX.1707 -16.IV.1788)

1. Жазықтықта арақашықтығы шырпының ұзындығына тең, параллель түзулердің жүйесі жүргізілген жазықтыққа шырпының бумасын лақтырды. Шырпының бір параллель түзумен қиылысу ықтималдығы –ге тең.

Европа XIX-XXғ

Жозеф Лун Лагранж (25.01.1736-10.10.1813)

1. Теңдікті тексер: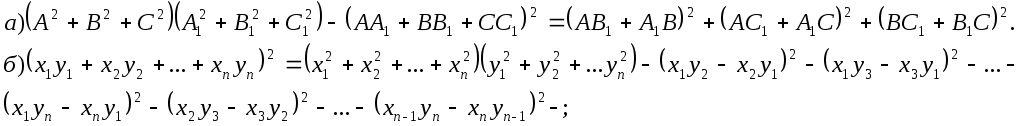



Карл Фридрих Гаусс (30.04.1777-23.02.1855)

1. Егер төртбұрыштың ешбір қабырғасы параллель болмаса, онда қарсы жатқан қабырғалардың қиылысу нүктелерін қосатын кесіндінің ортасы, диагоналдарының орталарын қосатын түзуде жатыр.
Симеон Дени Пуассон (21.06.1781-25.04.1840)

1. Бір адамда 12 пинт вино бар. (I пунт-0,568л). Ол адамда сыйымдылығы 8 және 5 болатын ыдыстар бар. 6 пинт виноны сыйымдылығы 8 пинт болатын ыдысқа қалай құюға болады.
Огюстен Лун Коши (21.08.1789-23.05.1857)

1. Кез келген т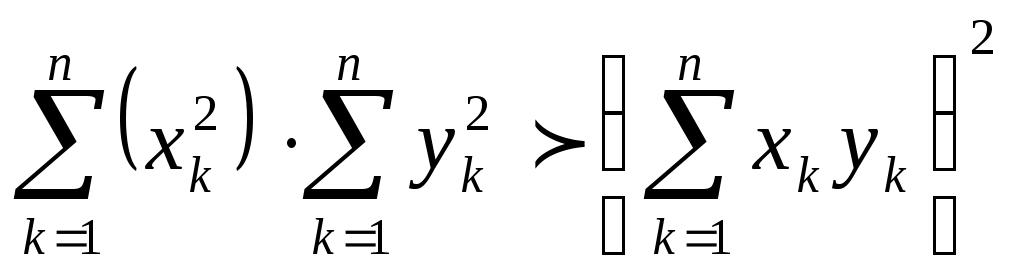еріс емес сандары үшін



2.

3. Ұзындықтары жеткілікті жақты болатын екі бірдей қағазды алып және олардан бір жақты бетті Мебиус парағы моделін дайындаңыз. Модельдің біріне жолақтың ортасынан қарандашпен сызық жүргізіңіз, ал екіншісіне жолақты 3 бірдей бөліктерге бөлетіндей 2 сызық жүргіземіз. Бірінші модельдің жолағын ортаңғы сызығынан, ал екінші модельдің жолағын 2 жүргізілген сызықтар бойымен қиықсыз. Нәтижесінде не пайда болады ?
Якоб Штейнер (18.03.1796-01.04.1863)

Бір ғана сызғыштың көмегімен орындалатын салулар.

1. Түзудің бойында А,В,С үш нүктесі берілген. В нүктесі А және С нүктелерінің арасында жатыр. Кез келген К(К(АС)) нүктесі арқылы (АС) –ға параллель түзу жүргізу керек.

2. АС║ КҒ берілген. Осы кесінділерндің біреуін, мысалы кесіндісін тең бөлікке бөліңіз.

3. Екі параллель түзулер берілген. Берілген нүкте арқылы берілген түзулерге параллель болатын үшінші түзу жүргізу керек.

4. Көмекші шеңбер және осы шеңбердің центрі арқылы өтетін (АВ) түзуі берілген. Берілген М нүктесінен (АВ) түзуіне перпендикуляр жүргізу керек.

5. Көмекші шеңбер және кез келген АВ түзуі берілген. Берілген нүкте арқылы өтетін және (АВ) түзуіне параллель түзу жүргізу керек.

6. Егер екі тік бұрышты үшбұрыштардың әрқайсысының бір катеттері және екінші катеттерінің қосындысы белгілі болса, онда үшбұрыштар ұқсастығы жағдайында гипотенузалар қосындысы ең кіші болады.

Нильс Генрих Абель (5.08.1802-6.04.1829)

1. болсын. Мұндағы ; -2 сандар тізбегі. онда болады.

1.Қарандаштың бір сызығымен а фигурасын, содан соң в фигурасын сызу керек. Бұл екі есептің шешімдерінің нәтижелерін немен түсіндіруге болады? А үшін- жоқ, в үшін-ия. Бұл топологиялық тапсырмалардың мысалдары. Тополдогия терминін енгізген Листинг.

Жозеп Лун Бертран (2.03.1822-3.04.1900)

1. Бірде Непольда преподобный Галиани Базиликидің бір адамын көреді. Ол үшін ойын сүйегін шеңберге лақтырып тұрды, және үш алтылық түсіремін деп айтты, шынымен ол үшін алтылық түсірді. Базиликидің адамына бұл екінші ретте, содан соң үшінші ретте, төртінші ретте, және бесінші ретте де түсті, «Вапха қаны» деді преподобный, «Сүйектер қорғасын жалатылған»

Чарлз Людвид Дозжс (Льис Керролл)

(27.01.1832-14.01.1898)

1. Он тиын жазықтықта екі картаға орналастырылған екі қатарға орналастырылған. Бес әртүрлі түзуде 4 тиыннан болатындай жағдайларға 4 тиынды орналастыру керек.

2. Патша өзінің қазынасы азайғанын және қалған ақшасын үнемдеп жұмсау керектігін түсініп өзінің ақылшы кеңесшілерінің көпшілігін қуып жіберуді ұйғарды. Ақылшылар патшада өте көп болатын. Оларға қойылатын жалғыз кінә-қандай да бір сұрақтар бойынша патшаға берген кеңестерінің қарама-қайшылығы және патша үстелінің тамағына және ішімдіктеріне шексіз қызығушылық. Бірақ заң бойынша сарайда, араларында екі көзге бір көздері көрмейтін екі соқыр, бес екі көздері де көреген, он бір көзге көреген болатындай, сонша кеңесшілер болуы тиіс. Заңның талабын бұзбас үшін сарайда қанша ақылшы қалады?

3. Бір адам театрға барғысы келеді. Билет 1 шилинг 6 пенс тұрды, ал ол адамға тек қана 1 шилинг болды. Ойлана келіп ол өзінің 1 шилингісін лавочникке залогқа беруді ұйғарды. Лавочник тиынды мұқият қарап шығып, және оның жалған емес екеніне көзі жетіп, ол адамға закладқа 9 пенсо берді. Кошологінде 9 пенсомен және бір шилингке квитанциясы бар ол адам лавочниктен кетіп, көшеде досын кездестіреді. Досына квитанцияны 9 пенсоға сатып алуды ұсынды. Енді бұл адамда лавочниктен алған 9 пенсо және квитанциясы сатқаннан түскен 9 пенсо бар. Бұл сомма билетке жететін еді. Барлық операциялар нәтижесінде кім және қанша жойғаны сұралады.

4. Бір адщам 5 сағат қыдырды. Алдымен ол горизанталь жолмен жүріп өтіп, содан coң тауға көтерілді және ақырында бұрын жүріп өткен жолмен бастапқы пунктке қайта оралды. Оның горизонталь жол бойымен жүріп өткен жылдамдығы 4км/сағ, тауға шыққандағы жылдамдығы -3 км/сағ, таудан түскен уақыттағы жылдамдығы -6 км/сағ болса, жүрген жолды тап.

Геоде Кантор

1. Серпинский кілемінің варианты: бірлік квадраты 25 тең квадраттарға бөлеміз және тек ортаңғысын алып тастаймыз( оның ауданы 1/25 ). Алынып тасталған квадраттың қабырғалары болатын кесінділерін үлкен квадратқа дейін созамыз. Әрқайсысынан ( алынған квадраттардан олар төртеу ) және 4 тіктөртбұрыштан екі 1/25 болатын өзара перпендикуляры жолақтар саламыз. 4 квадрат және 4 тіктөртбұрыш қиылысатын жолақтардан 8 кв алып тастаймыз. Лынған квадраттардың ауданы 8/25 үшінші қадамға барлық ауданнан 64 квадрат алып тастайтындай осындай салу орындаймыз. Серпинск кілемі вариантының ауданы қандай?

Отандық математика.

2. Бірінші адамға және бірнеше адамдардың екеуіне бірдей тиетіндей, бір жарым дирхеманы бір адам және тағы бірнеше адамдар арасында бөлу керек. 1-ші адамнан басқа қанша адам болды.

Анания Ширакаци (VIIғ ортасы)

1. Бір көпес 3 қалада болып сауда жасағанда, ол 1-ші қалада мүлкінің жартысын және үшт ен бірін, 2-ші қалада ( қалған мүлкінің )жартысын және үштен бірін, 3-ші қалада тағы да ( қалында барының) жартысын және үштен бірін баж салығ,ы ретінде төлеген, сонда үйіне қайтып келгенде 11 ақшасы (ақша бірліктері) қалған. Сонымен, әуелде көпестің барлық ақшасы қанша еді, соны біл.

2. Афина қаласында хауыз (су қоймасы) болған еді және оған 3 құбыр жүргізілген болатын 1 –ші құбыр хауызды 1 сағат ішінде, 2-ші құбыр 2 сағат ішінде, 3-ші құбыр 3 сағат ішінде толтыра алатын. Барлық 3 құбырды қтарынан ашқанда олардың хауызды сағаттың қандай бөлігі ішінде толтыратынын біл.
П.Л. Чебышев (16.04.1821 – 6.12.1894)

1. Егер және болса, онда


Егер де , бірақ болса, онда



Бұл теңсіздік тек қана және болғанда ғана орындалады.

а)

б) болғанда Чебышев теңсіздігін тексеріңіз.

Лев Николаевич Толстой

1. Шапқыншылар артелі бірі екіншісінен екі есе үлкен болатын екі көгалды шаба алады. Күннің бірінші жартысында барлығы бірінші көгалды шапты. Түстен кейін артель екі бірдей группаға бөлінді. Бірінші группа үлкен көгалда қалып кешке дейін шапты. Екінші группа кешке дейін кіші көгалды шапты, бірақ бұл көгалда кішігірім бөлік қалды. Оны келесі күні бір шапқыншы шауып тастады. Артельде қанша шапқыншы болды.
2. Суда өсіп тұрған тал су бетінен бір аршынға шығып тұр. Талды өлшемей және тереңдікті не ескекпен, не басқа заттармен өлшемей, тал өсіп тұрған өзеннің тереңдігін табу керек.
3. Ұзындығы мен екі қандай да бір өлшем болатын бөлменің қарама – қарсы жақтарында шыбын мен өрмекші отыр. Шыбын еденнен 1,5 аршында, ал өрмекші төбеден 1,5 аршында отыр. Шыбын мен өрмекші араларының ең қысқа арақашықтығын табу керек.
Эйлер есебі.

1. Бір санның 4-ші дәрежесін сол санның жартысына бөлгенде және ге

арттырғанда 100-ге тең болу керек. Сол санды тап.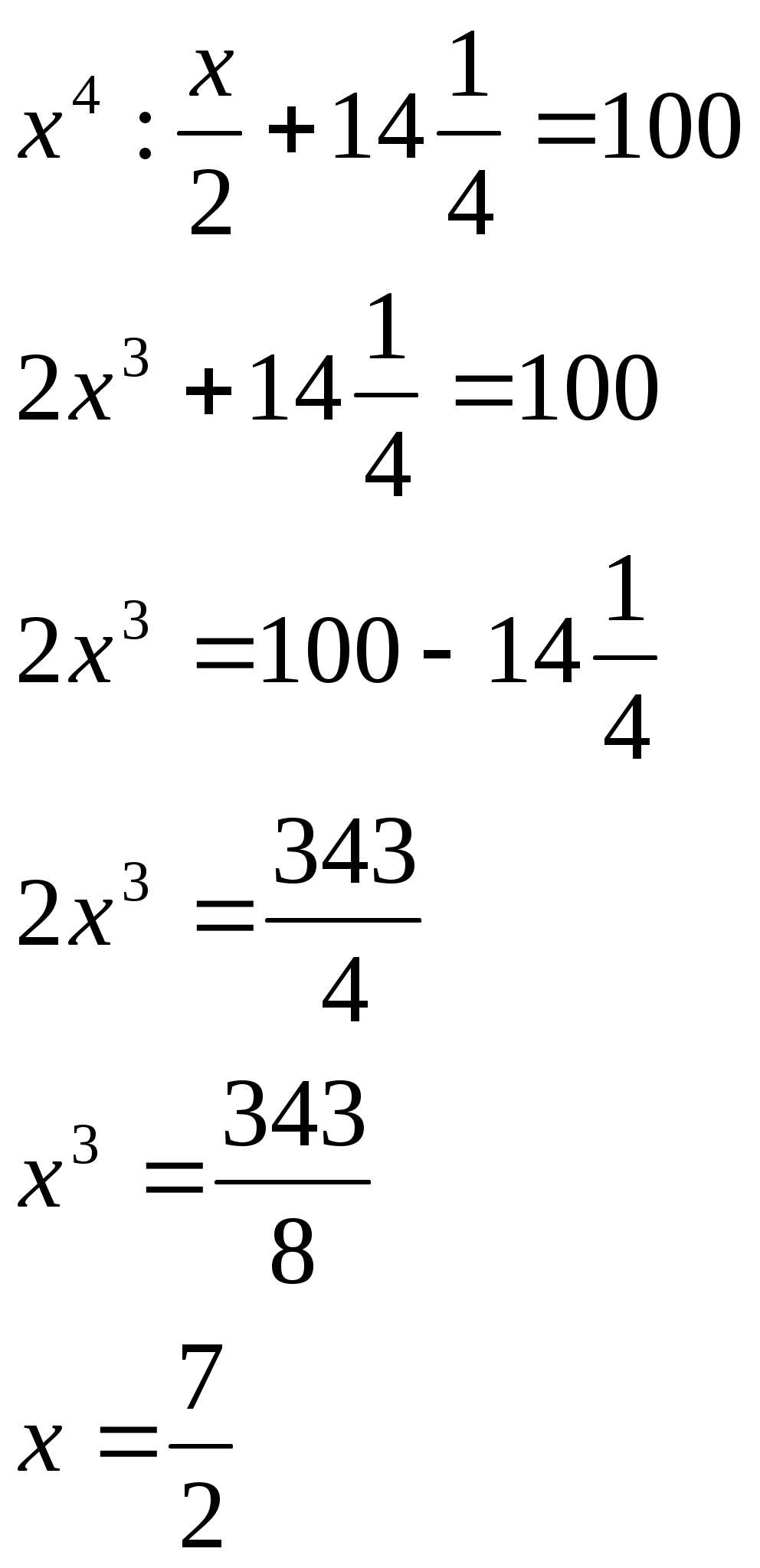


Жауабы: ;

2. Үш адам 24000 ливрға үй сатып алғысы келді. Олар былай келісті: біріншісі жарты ақшасын береді; екіншісі үштен бірін береді, ал үшіншісі қалған бөлігін береді. Әрқайсысы қанша бермек?

I-ші: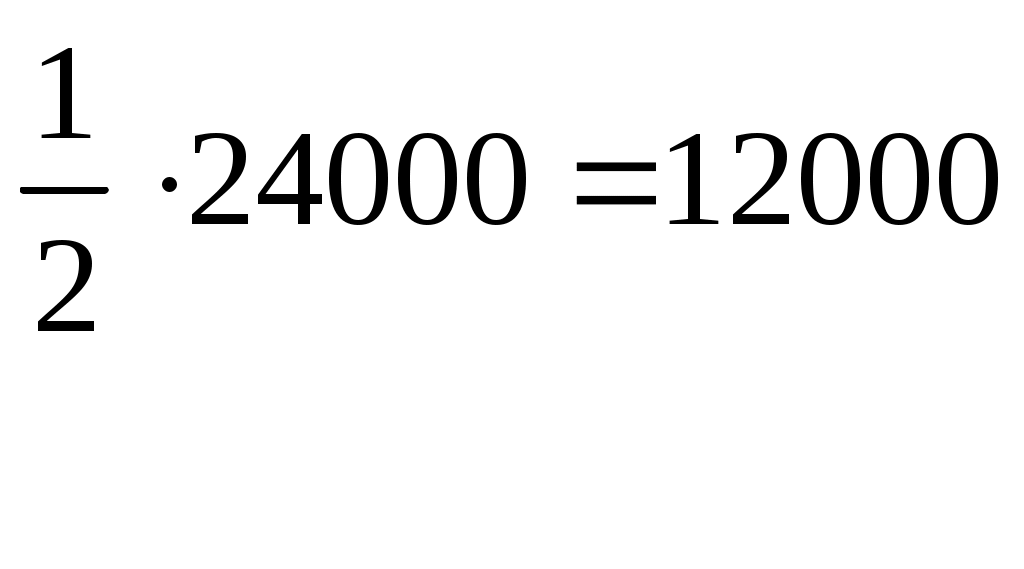

II-ші:

III-ші:

Жауабы:

3. Бір топ қаз ұшып барады, оларға бір қаз қарсы ұшып келе жатып: «Жүз қазға бір сәлем!» - депті. Топ қаз оған былай деп жауап беріпті: «Жоқ біз жүз емеспіз! Егер бізге тағы осынша қосылса, тағы соның жартысындай, тағы соның ширегіндей, оның үстіне сен қазым, бізге қосылсаң, біз тура жүз қаз боламыз» Олар қанша болған еді?

Шешуі: қаз саны – х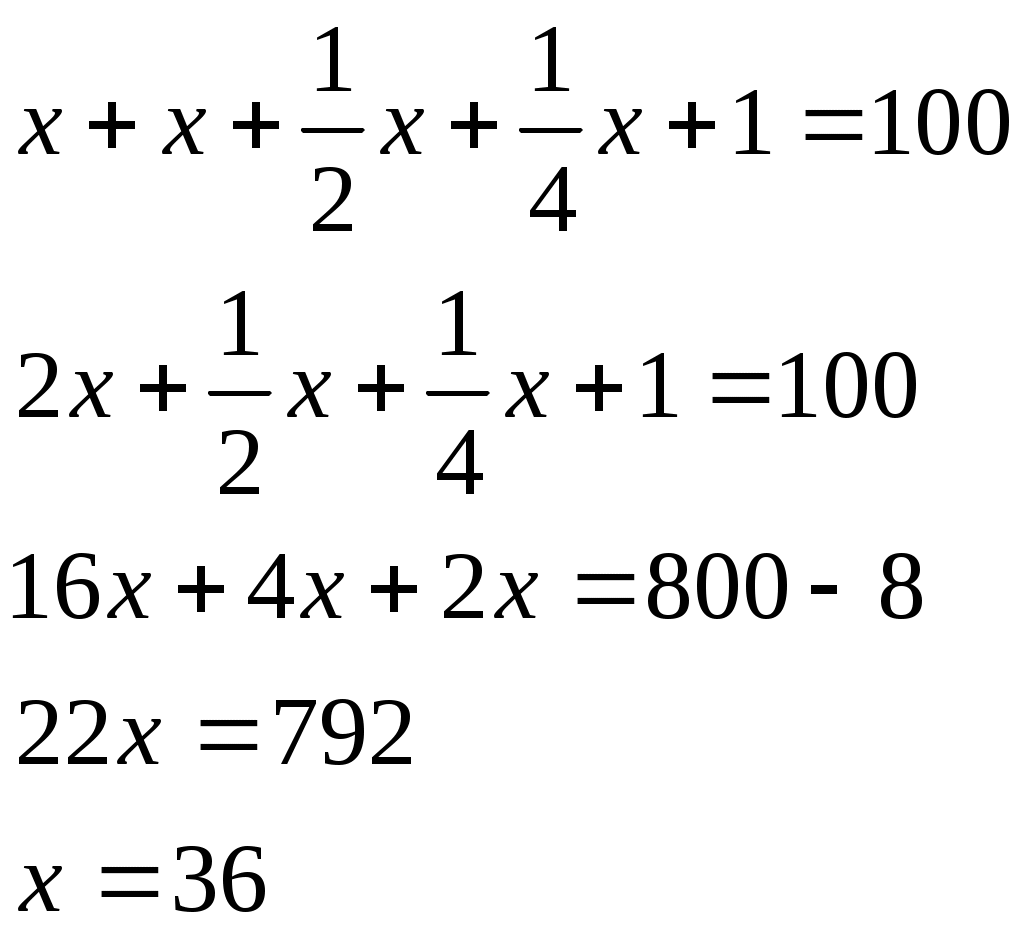



Жауабы: қаз.

4. Бехаэддин есебі.

Өзінің үштен екісіне және бірлікке арттырылған сан 10-ға тең. Сол санды табу керек.

Шешуі: Ізделінді сан – х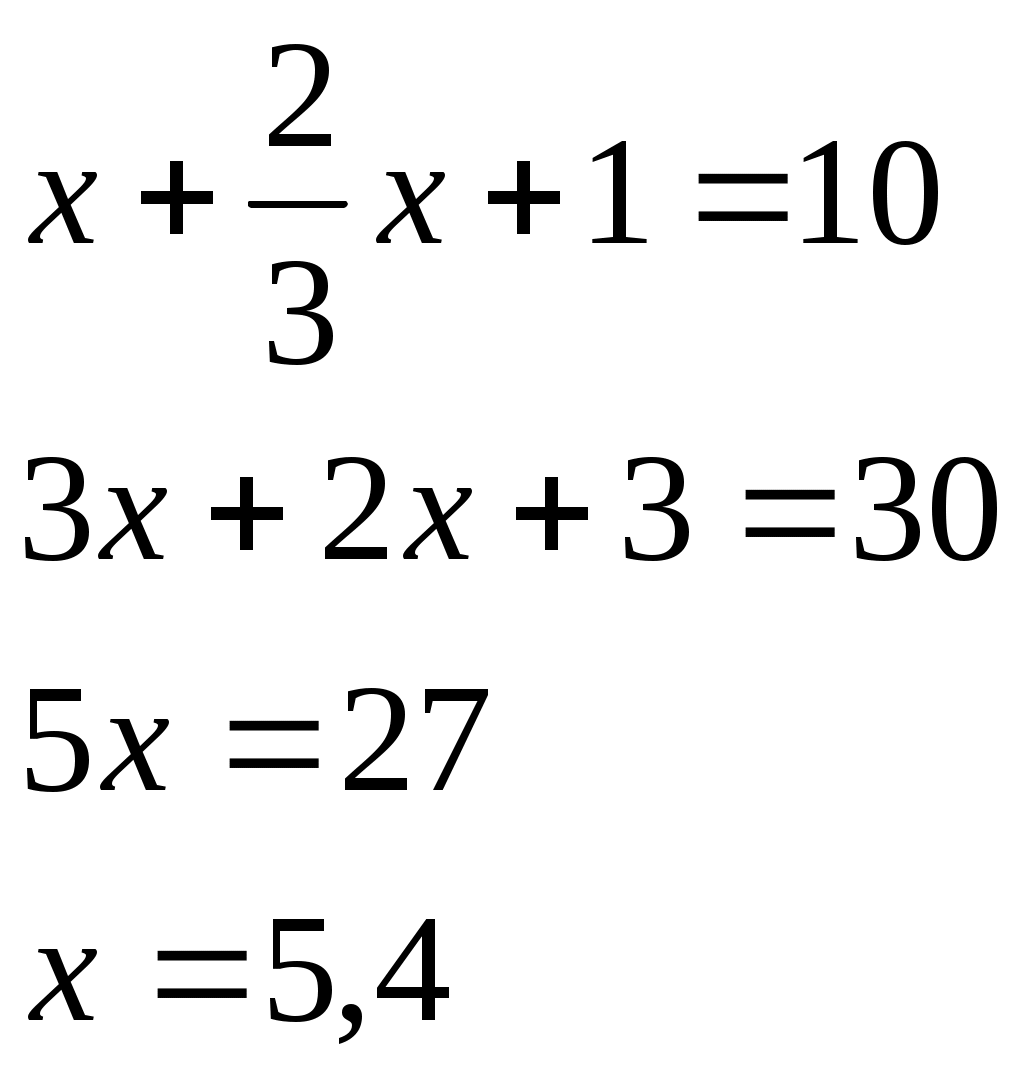



Жауабы:

5. «Үш адам ақша ұтып алған. I адамға осы соманың і, II адамға осы

соманың і, III адамға 17 флорин тиді. Ұтыстың шамасы қандай болған?»

Шешуі: Ұтыс шамасы – х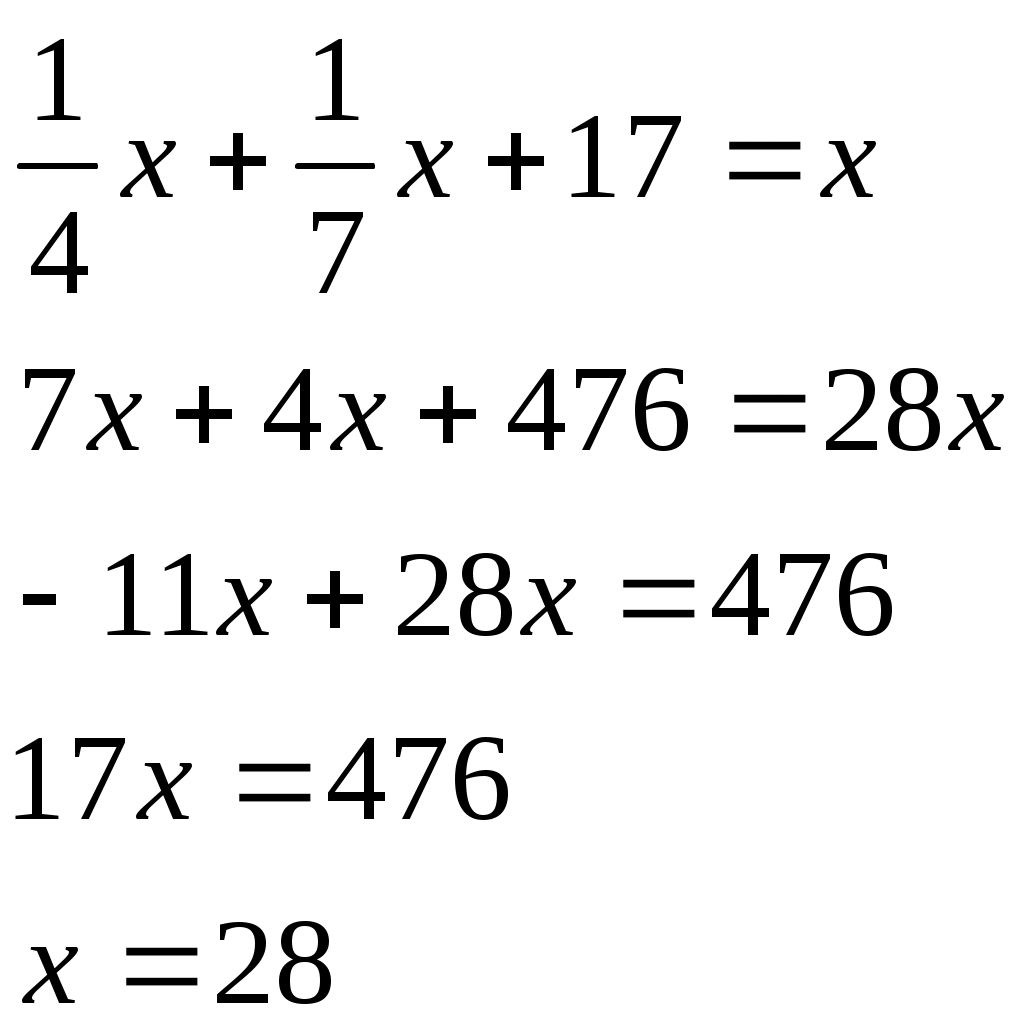


Жауабы: флорин.

6. «Бір адам жыл аяғына дейін киім және 10 флорин алмақшы болып жалданды. Бірақ 7 ай өткен соң жұмысты тоқтатты да, есеп айырысқанда киім және 2 флорин ақша алды. Киім қаншаға бағаланған?»

Шешуі: киім – х

1 жылда –

7 айда –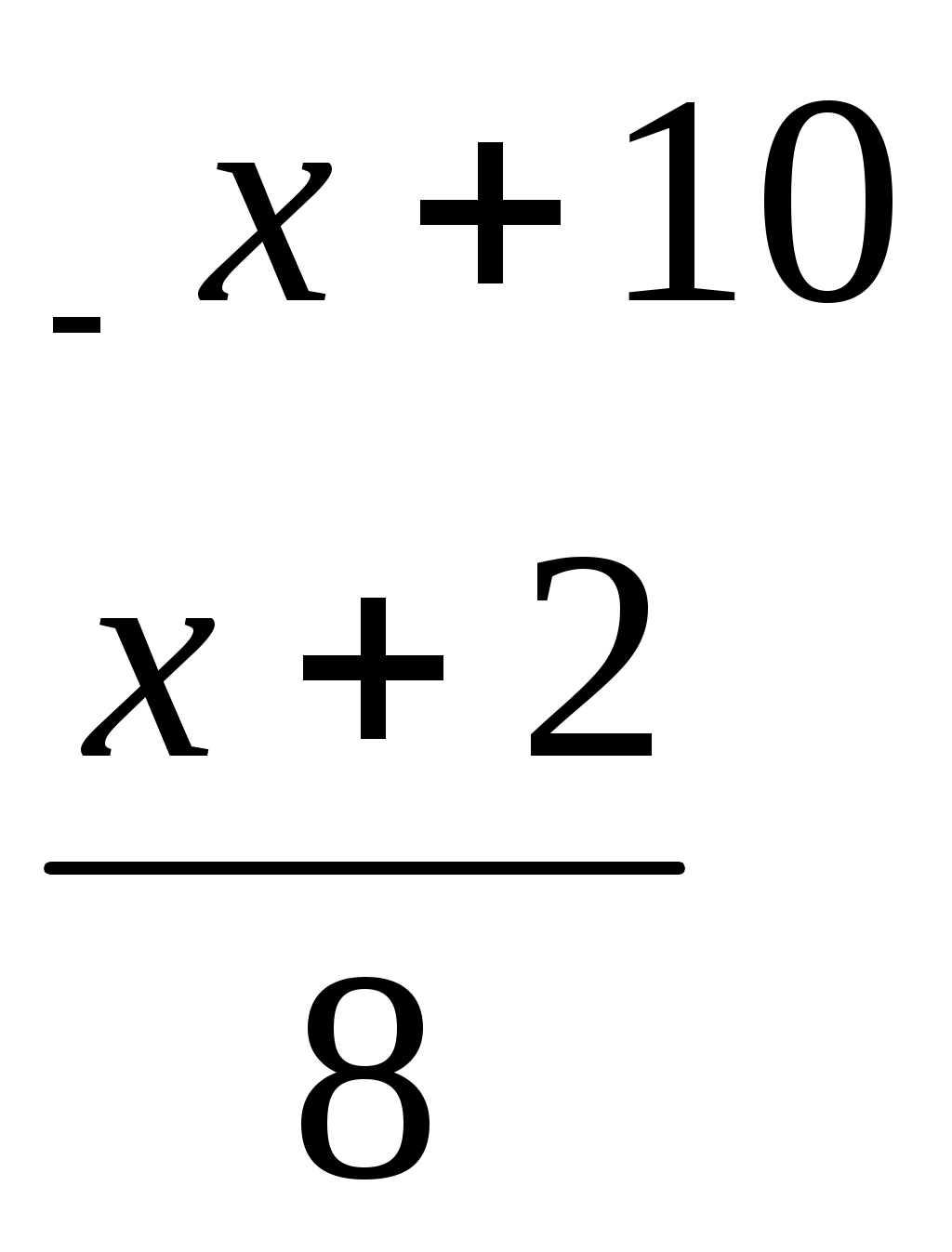

айға = 1,6



1,6 · 12 = 19,2 ( 1жылда)

х + 10 = 19,2

х = 9,2

Жауабы: 9,2.

7. «Тоғыз кітаптағы математикадан» есеп. Бірнеше адам бірлесіп тауық сатып алған. Егер әр адам 9-дан (ақша бірлігі) берсе, онда 11 қалады, ал егер әрқайсысы 6-дан берсе, 16-сы жетпей қалады. Адам саны мен тауықтың құнын табу керек».

Шешуі: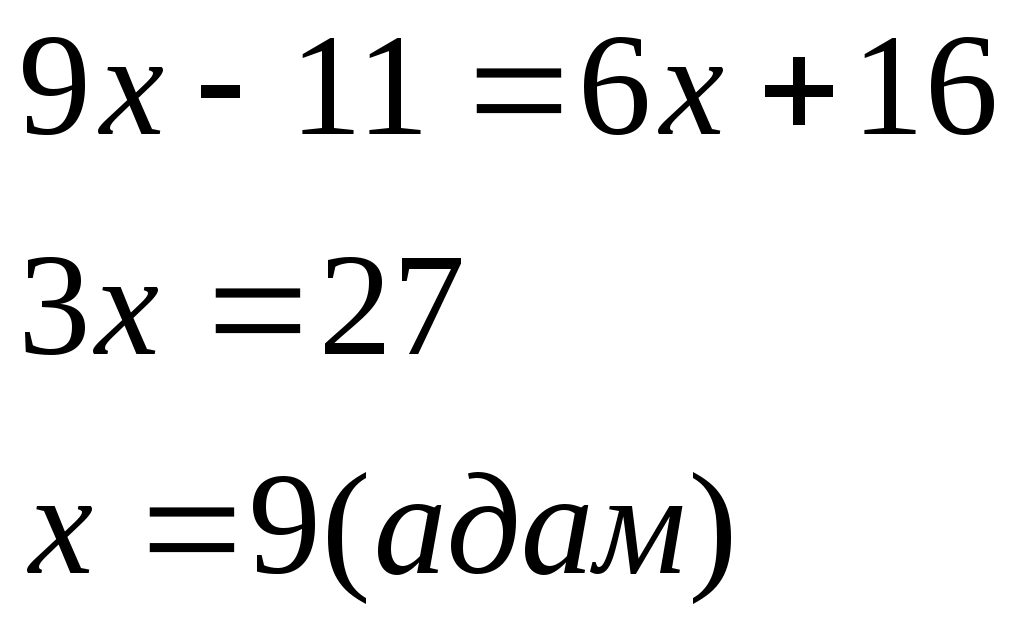



8. «Егер бір санды 20-ға қоссақ және сол санды 100-ден алсақ, сонда шыққан қосынды сонда шыққан айыпмадан 4 есе артық болады. Белгісізді табу керек.»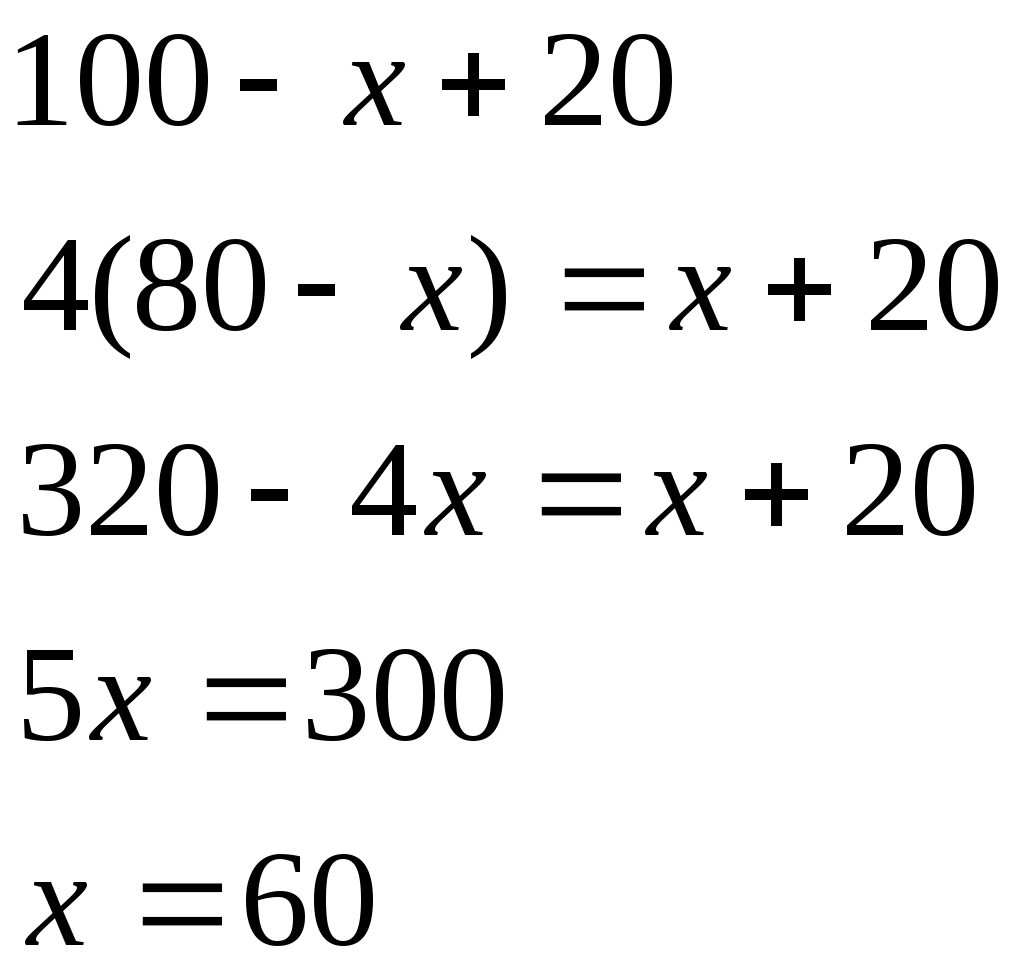



Жауабы: 60.

9. Акмим папирусынан (VI ғ. ) есеп: «Бір адам қазынаның - ін алды. Одан қалғанының - ін екінші біреу алды. Ол қазынада 150 қалдырды. Әуелде қазынада қанша болғанын білгіміз келеді?»

Барлығы – х
І - х

ІІ -
Қалды – 150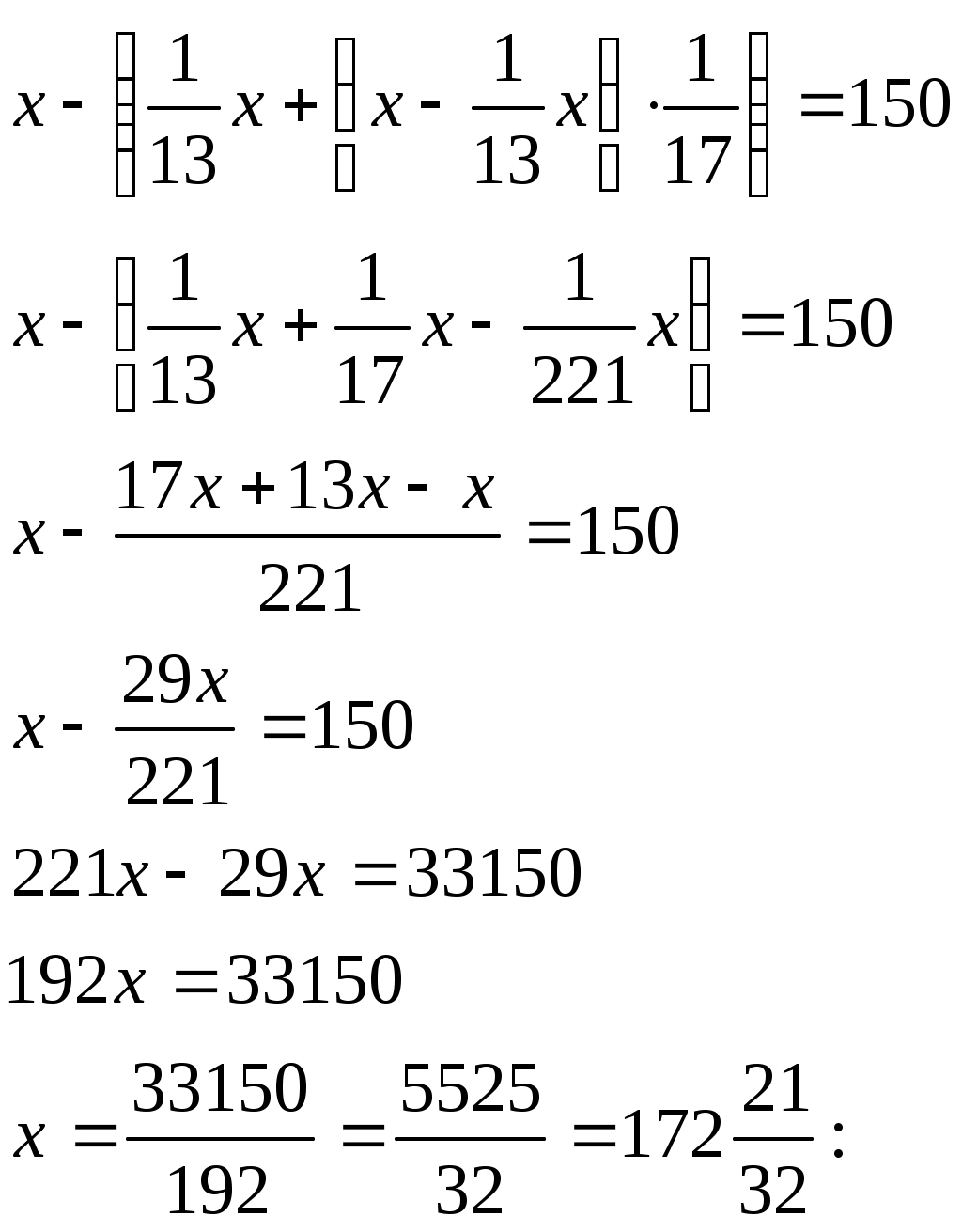

10. Диофанттың қабіріндегі құлпытаста былай деп жазылған: «Диофанттың балалық шағы - өмірінің алтыдан бірі, жастық шағы – он екіден бірі, ал баласыз өткен ерлі-зайыпты өмірінің жетіден бірі және тағы 5 жыл өткенде

ұлды болды. Әкесінің жарты жасына келгенде ұлы дүние салды, бұдан кейін Диофант тек 4 жыл ғана өмір сүрді. Диофант неше жыл сүрген еді?»

Шешуі: Өмірі – х

Балалық шағы - х

Баласыз - х

Жастық шағы - х

Ұлды - ;

Ұлы дүние салды - ;

Өзі дүние салды - ;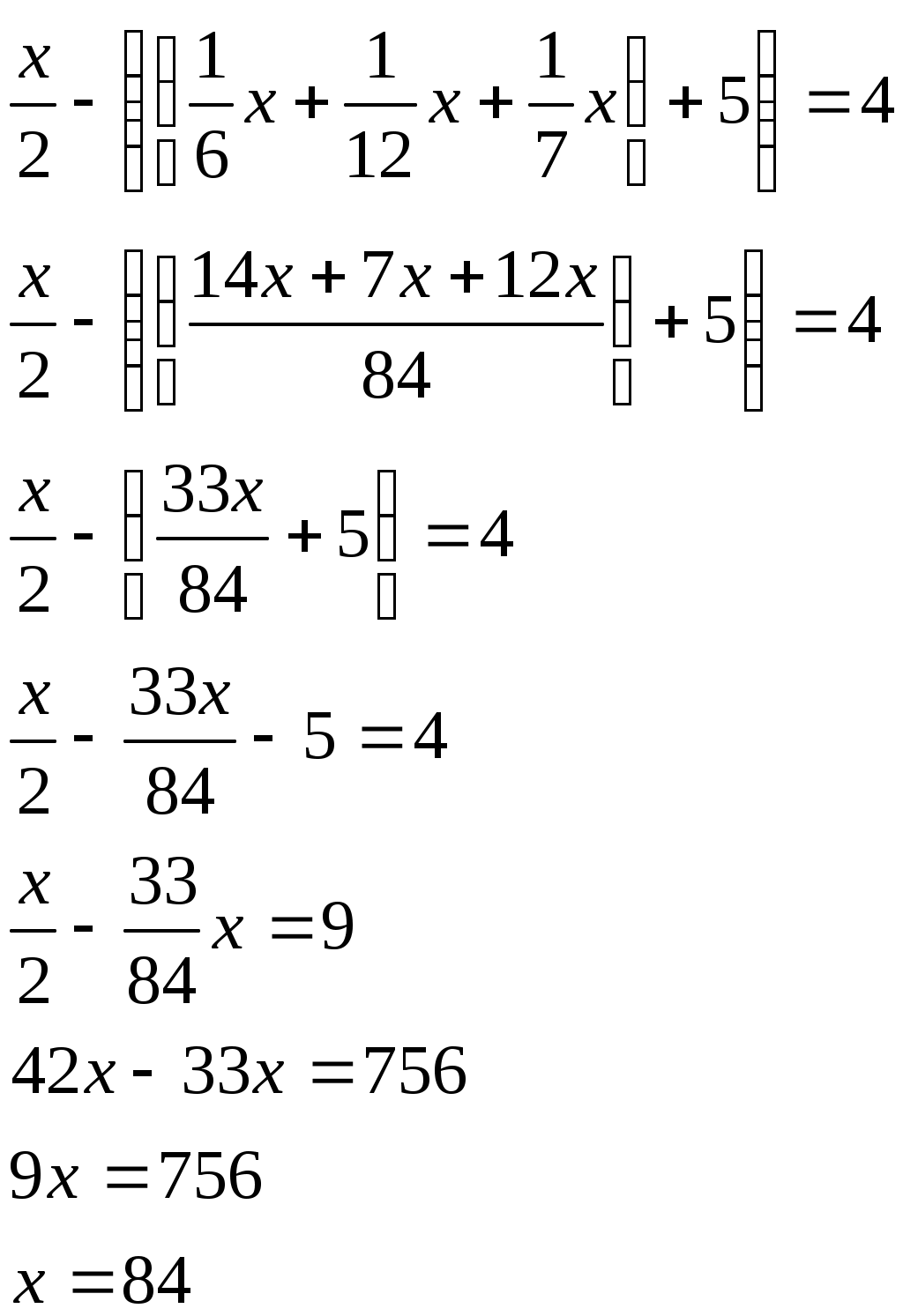


Жауабы: Диофант 84 жыл өмір сүрді.

11. «Көпестің жинақтаған азды-көпті ақшасы бар еді. Ол жыл сайын семьясының қажетіне 100 фунт ақша ұстап, қалған ақшасына оның үштен біріндей ақша қосып отыратын. Үш жыл өткеннен кейін ол қаражатының екі есе көбейгендігін байқады. Әуелде оның қанша ақшасы болған еді?»

Бар еді – х

Бір жылдан соң қолында қалды – х – 100

Үш жылдан соң болды - ;

Жинақталған ақшасы әуелгі ақшасынан екі есе артық болды.

Шешуі: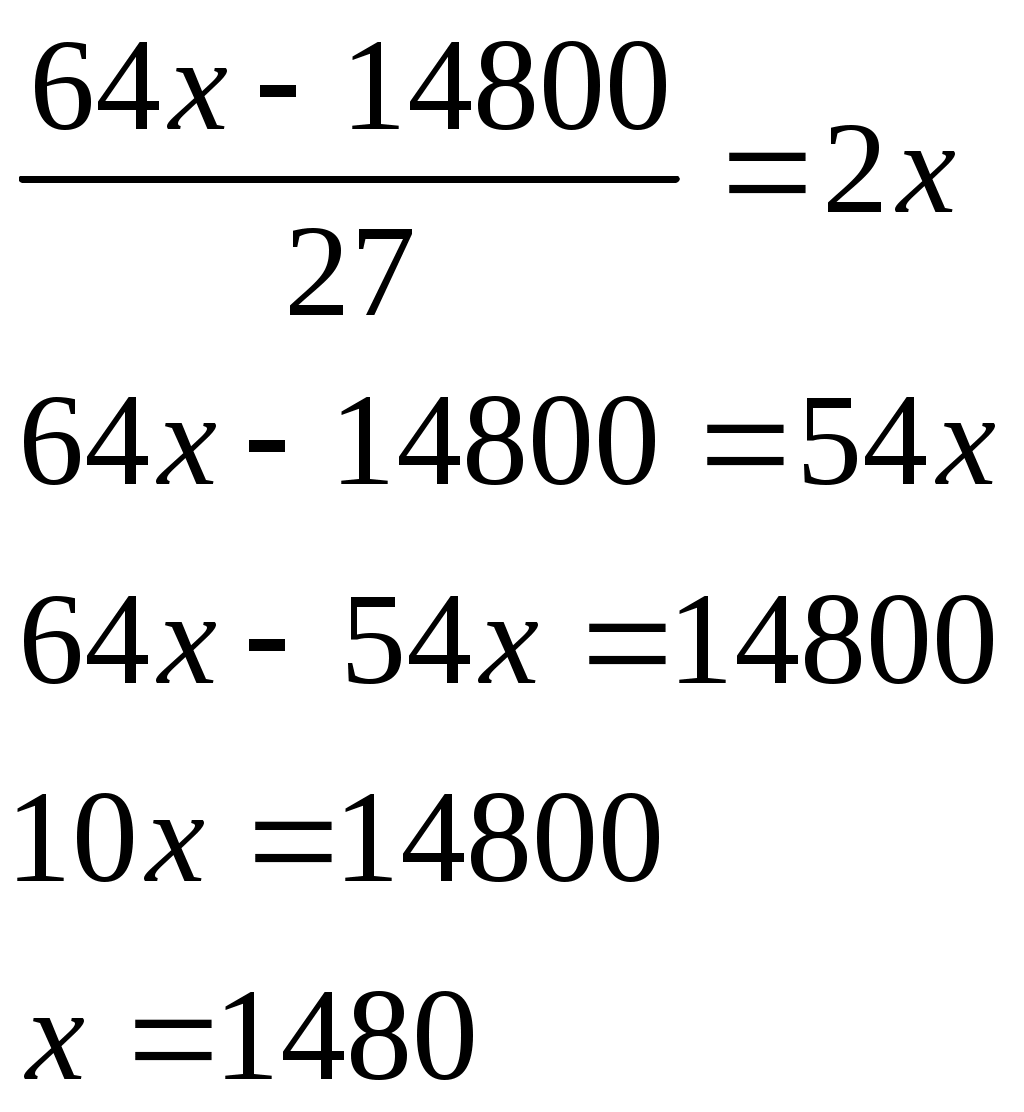

Жауабы: Әуелдегі ақшасы 1480 фунт.
12. «Бақташы 70 өгіз айдап келеді. Оған мынадай сұрақ берілген: Үлкен табынының бұл айдап келе жатқаның қанша?

Бақташы жауабы:

− Табындағы барлық малдың үштен бірінің үштен екісі.

Есептеп көр!»

(Бүкіл табында қанша өгіз болғандығын білу керек.)

Шешуі: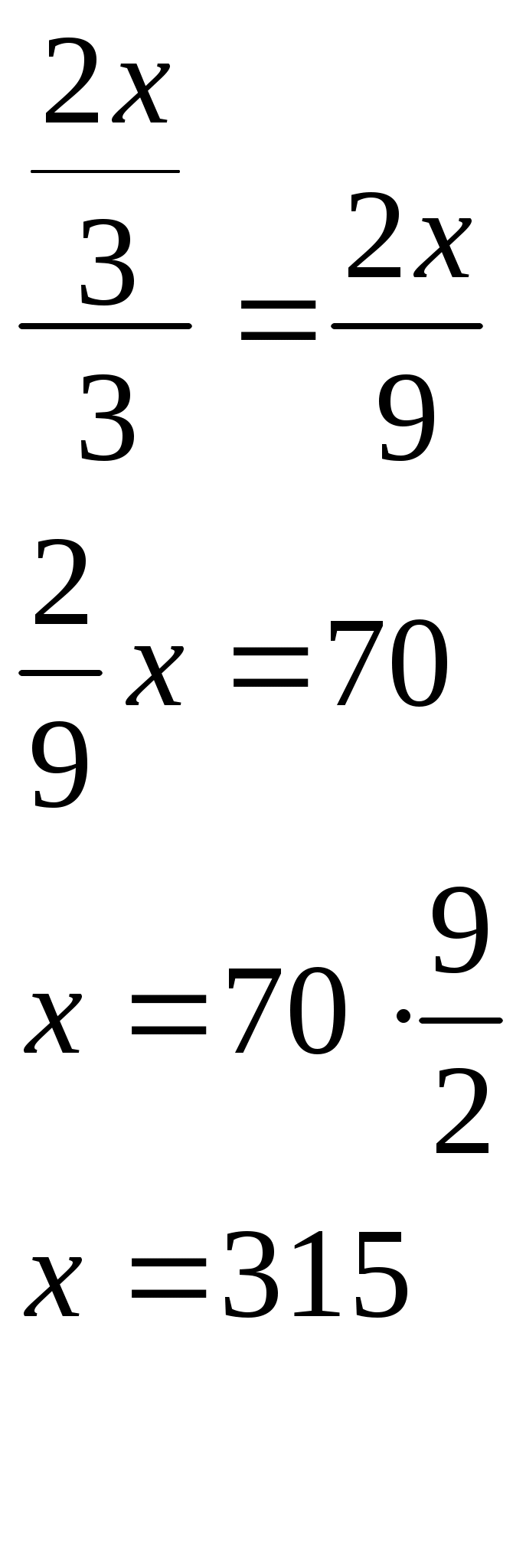



Жауабы: Бүкіл табында өгіз болған.

13. Ежелгі римдік есеп. ІІ ғ. «Бір адам өлерінде былай деп өсиет қалдырған: егер әйелім ұл тапса, онда оған имениемнің - сі, ал әйеліме қалған бөлігі берілсін. Егер қыз туса, онда оған - і, ал әйеліме - сі берілсін. Егіз бала – қыз және ұл туды. Имение қалай бөлінуі керек?»

Жауабы: Ұлы әйелінен екі есе көп үлесін, әйелі – қызынан екі есе көп үлесін алуы тиіс. Имениені ұлы, әйелі және қызына 4:2:1 сандарына тура пропорционал етіп бөліп берген жөн.

14. Бір адам өзінің досына: «Маған 100 рупий бер, сонда мен сенен екі есе бай боламын» - депті. Досы былай деп жауап береді: «Сен маған тек 10 рупий бер, сонда мен сенен 6 есе бай боламын». Әрқайсысында қанша болған?

Шешуі:

I адам – х

ІІ адам - у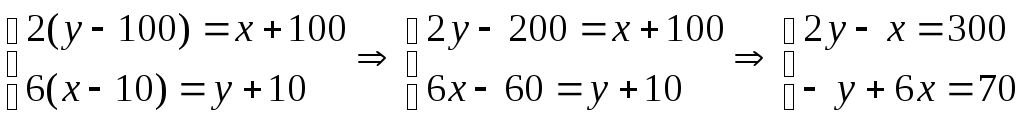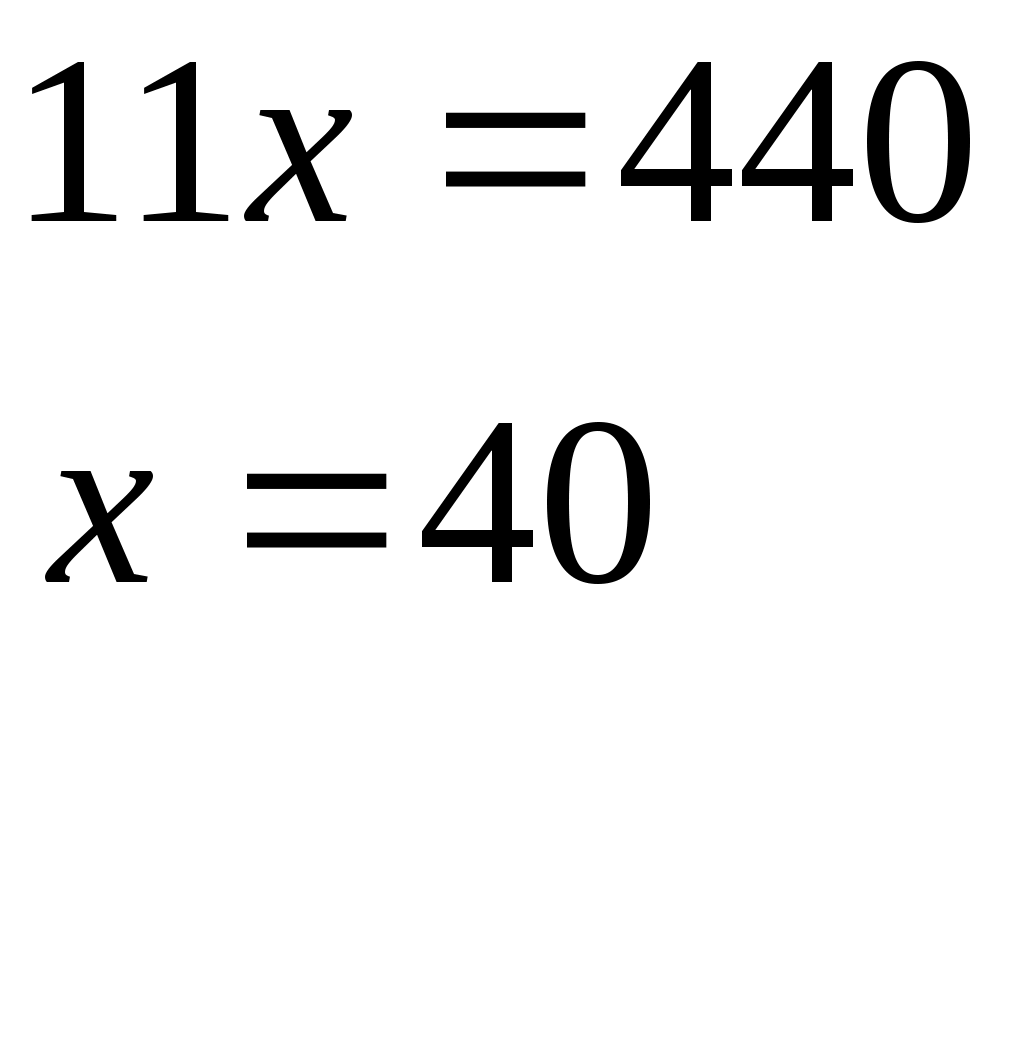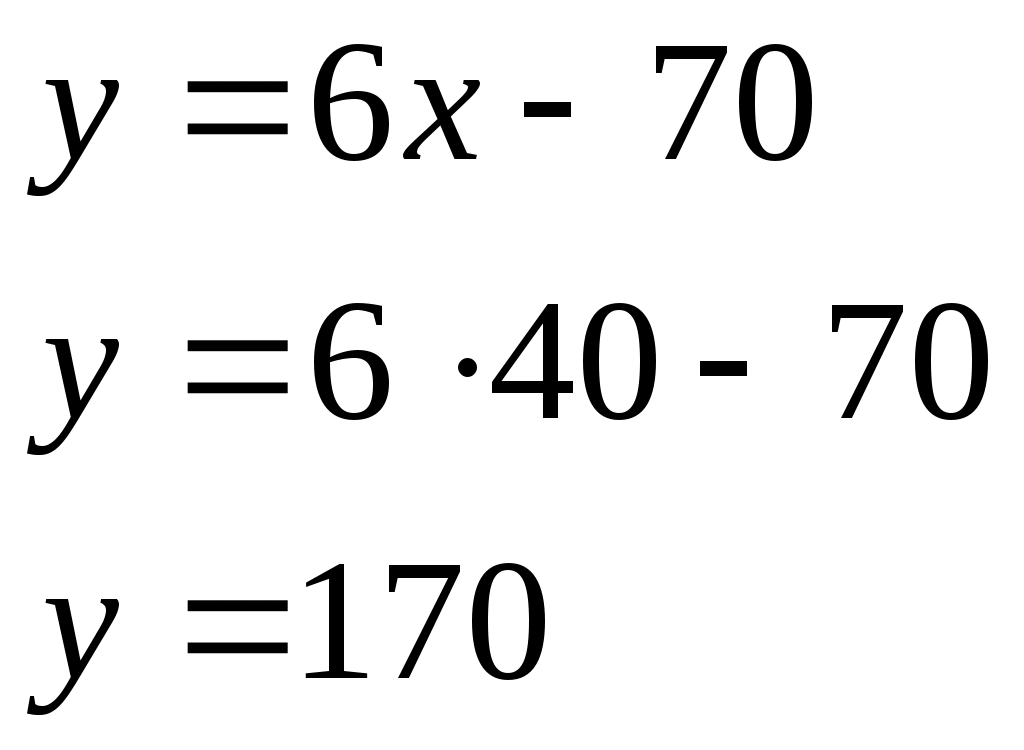



Жауабы: және ;
15. «Екі санның айырмасы екіге тең, ал олардың қатынасы екіге кері санға тең. Осы сандарды табу керек».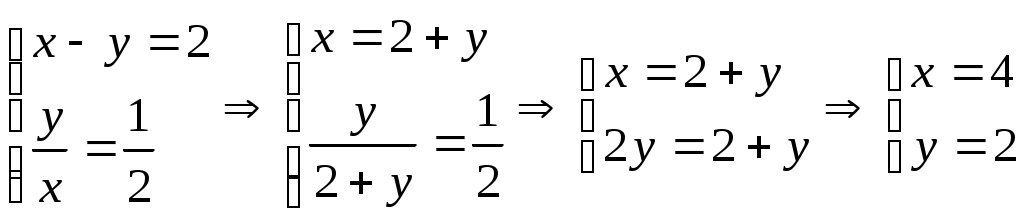
Жауабы: 2; 6.
16. «Репетитор» деген әңгімесінде ұлы орыс жазушысы А.П.Чехов мынадай есеп келтіреді: «Көпес 138 кез қара және көк шұғаны 540 сомға сатып алды. Егер бір аршын көк шұға 5 сом, ал қара шұға 3 сом тұрса, әрқайсысынан неше кез мата алған?»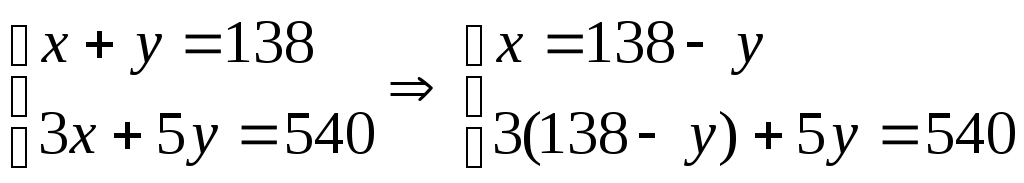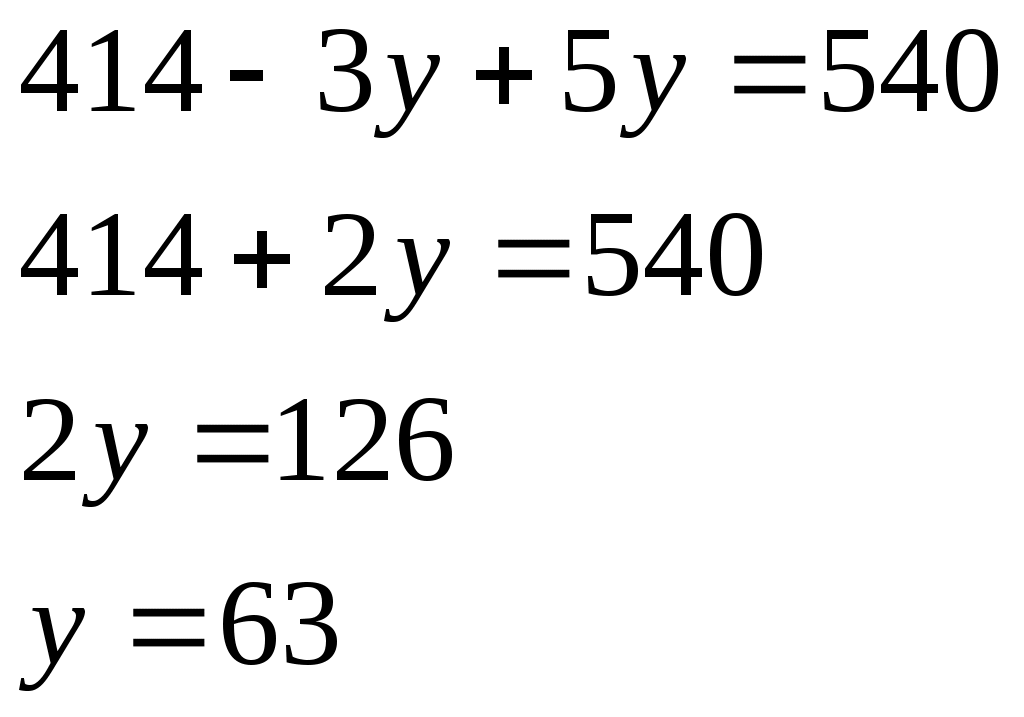



17. XVI ғасырдағы иран ғалымы Бехаэддиннің есебі: «10 санын айырмасы 5 болатын екі бөлікке бөлу керек».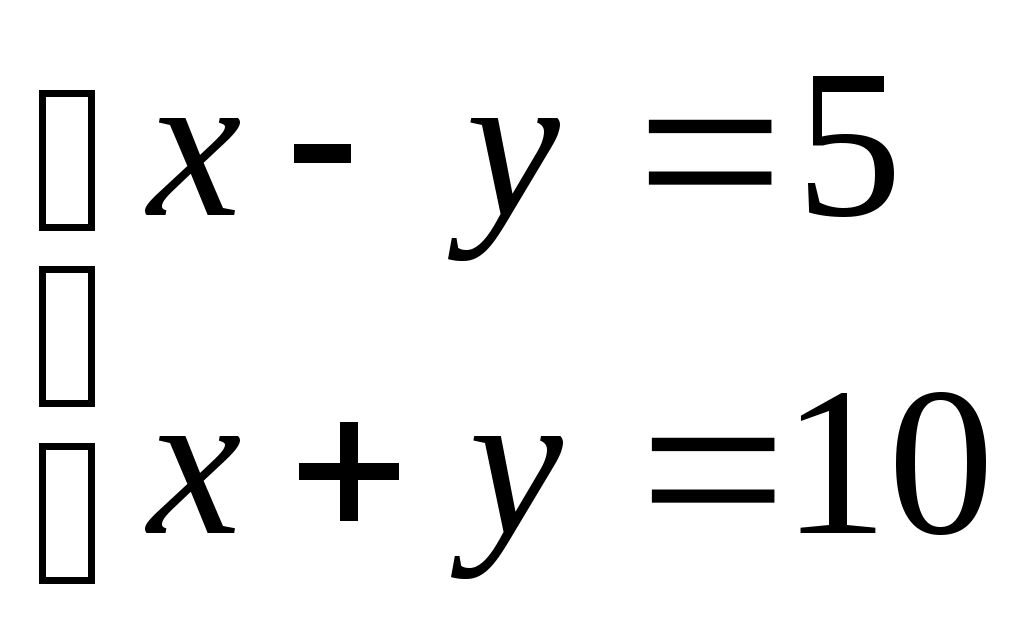



18. «Екі санның қосындысы 10-ға, ал қатынасы 4-ке тең екенін біле отырып, сол сандарды табу керек».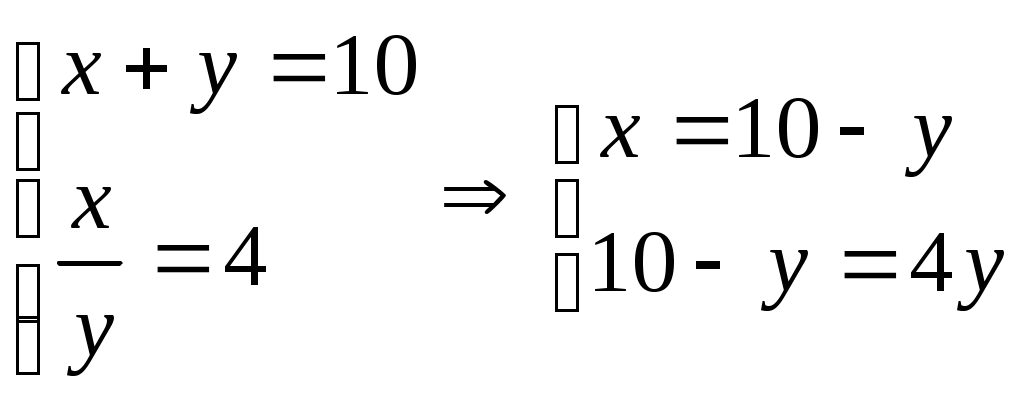






19. Евклид бастамалық ІІ кітабында берілген теңбе-теңдікті тексеру.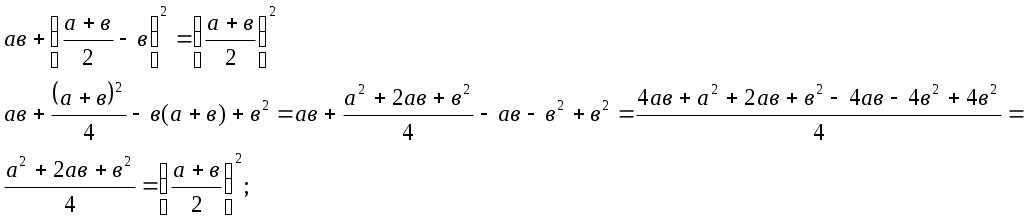



20.


21.


22.



23.

24. Диофанттың «Арифметикасында» баяндалған бөлшектермен берілген мына амалдарды тексеру керек: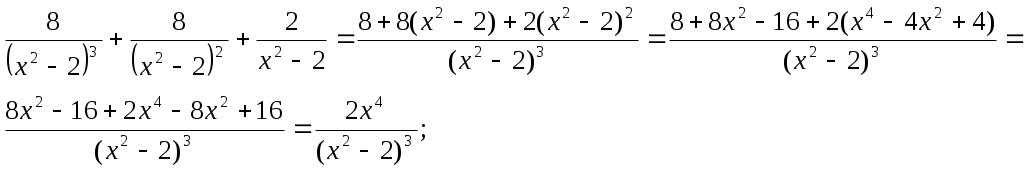


25.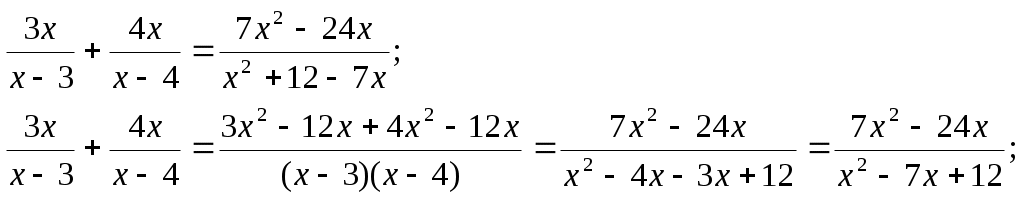


26.
27.

28.



Штифельдің «Арифметикасында» берілген бөлшектерге қолданылған мына амалдарды орындаңдар:
29.
30.
31.
32.
33. Ньютонның «Жалпыға бірдей арифметикасынан» бөлшектерді қысқарту.

34.

1. Математика бастамалары.

1. 
   Математика және оның тарихы.
   
2. 
   Математика ұғымдарының қалыптасуы.
   
3. 
   Ежелгі шығыс ғалымы.
   
4. 
   Мысыр математикасы.
   
5. 
   Вавилон математигі.
   

1. Математика тарихының методологиялық негізгі диомктикалық материолизм болып табылыды. А.Н Кормогоровтың тарауы бойынша математика тарихын шартты түрде 4 дәірге бөлуге болады.

І–дәуір. Математиканың туу, математикалық білім дағдылардың мағлұматтардың жиналу және қорғалу дәуірі. Бұл жазба тарихқа дейінгі санаудан алғашқы қарқынмен басталып математика өзінің белгілі бір зерттеу пәні мақсаты әдістері бар дербес теориялық ғылым болы қалыптасқан грек математиктарына (б.з.д 6-5 ғасыр) дейін созылады. Бұл дәуірде математикалық негізгі ұғымтар сандар, фигуралар т.б-лар қалыптасады.

ІІ-дәуір. Элементарлық математика дәуірі б.з.д 6-5 ғасырлардан басталып б.з 16-ғасырмен аяқталады. Бұл кезенде математикада тұрақты шамалар қалыптастырылады. Математиканың алгебра, геометрия және тригонометрия деп аталған дербес салалары пайда болады.

ІІІ-дәуір. Айнымалы шамалар математиканың туу дәуірі бұл кезенде математиканың негізгі нысанасы, объектісі – процестерді, қозғалыстарды зерттеп білу игеру басталады. Бұл дәуір 17–ші ғасырдағы Декарт, Лейбниц, Нютонның алғашқы математикалық жазбаларынан басталып 19-шы ғасырдың 1-ші жартысын қамтиды. Бұл аралықта математиканың бұрынғы салаларына аналитикалық геометрия, диферинциалдық және интегралдық есептеулер, диференциялдық теңдеулер, ықтималдық теориясы сияқты физика математика техникалық тағы басқа салалары қосылды.

ІV–дәуір. Қазіргі математика дәуірі. Бұл 19–ғасырдың 1-ші ұлы математиктер Н.И Лабочевский, Эрност Гауус ашқан математикалық жетістіктен басталады. Мұнда математика қамтитын кеңістік пішіндері мен сандық қатынастар мейлінше кеңейді сандардан басқа вектор, тензор тәрізді және басқа тектес шама қарастырыла береді кеңістік туралы ұғымның шеңдері кеңеліп әртүрлі геометриялар (Евклидтік елос) ашылады. Алгебраның мазмұны біртіндеп озгеріске ұшырайды. Математиканың көптеген жаңа шамалары қалыптасады. Математиканың өзінің тарихы логикалық және философиялық тұрғыдан негіздеу мәселесі қолға алынды есептегіш машиналар жасалды.
2. Карл Гаусс (неміс) математиканың әртүрлі салаларын әртүрлі сарапқа сала келіп арифметикалық математика патшасы деп бағалаған, арифметикалық негізгі ұғымы - сан. Олай болса сол сан ұғымының қалай пайда болуын ашу, білу үғымы математиканың үлкен проблема. Арифметика өзі айрықша ғылым болып бертінше қалыптасқан мен оның басты ұғымы сан ұғымы өте ертеде адамзат жазу сызуды білмеген заманда пайда болды. Адам баласы ең бірінші қолдана білген математикасының амалы санау болды. Тіпті аз ғана сана білетін жабайы тайпа көп нәрсе турулы жиндарды санауға дейін әрекет жасағанда адам санан бұрын-ақ санауды түгелдеуді білген деуге болады. Осы санау түгелдеу әрекеттер негізінде сан ұғымы туады біртіндеп кеңейеді.

Сан ұғымы баяу дамыды, сандар шекарасы біртіндеп кеңейді, тор ел бұғазының жағалауын мекендеген австралиялық жабайы тайпалар адам дене мүшелері арқылы 33-ке дейін санды өрнектей алады екен. Егер саннан сан асып кетсе таяқша пайдаланған. Қоғамдық өндірісті өркендеуі, өндірістің өнімнің молайуы тайпалар, қауымдар арасындағы саяси шаруашылық қарым- қатынастың ұлғаюы санның оған әртүрлі амалдар қолданудың дамуына әсер етті. Сандардың жоғарғы шекарасы біртіндеп кеңейіп натурал сандар қатары түзілді. Бертін келе жай сандардың әрқайсысы белгілі бір жүйемен атау, таңбалау күн тәртібіне қойылды. Міне осылай түрліше санау жүйесі немесе номерлеу қалыптасты. Санау жүйелерінің ішінде тарихи жағынан ең алғашқы және ең қарапайымы екілік жүйе. Қазіргі қолданылып жүрген позициялық жүйесі, яғни 10 цифр 0 1 2 3 4 5 6 7 8 9 арқылы кез-келген сандық өрнек жүйесі бізге көне үнді жұртынан мирас болып қалған. Сан ұғымы қалыптасуымен қатар сандарға 4 амал қолдану әрекеті туып жетілді. Сан ұғымы негізгі бөлшектер бүтін оң сандар сияқты күнделікті тұрмыста қажеттілітен шықққан. Түрліше ұзындық, аудан, көлем, уақыт т.б. шамаларды өлшеу барысында пайдаланды. Олар есептеу практикасында қолдауын тапты. Қорыта келгенде, арифметиканың бастапқы да негізгі ұғымдарымен әдістері тікелей өмір талабынан туындаған. Теріс, иррационал, комплекс, гиперкомплекс сан ұғымдарының шығуы, сан ұғымының дамуының заңды жағдайы және оларды математиканың ішкі даму талабы туғызды.

Геометрия ғылымының негізгі ұғымы болып саналатын фигураның ұғымдарының қалыптасуының арифметика негіздерінің шығуы ұқсас. Геометрия ерекше «гео»-жер «метрейн» - өлшеу деген екі сөзден құралған осы атаудың өзінен-ақ геометрияның шығу тегі бірден байқалады. Әр түрлі өлшеу қажетіліктердің ұзындық,аудан, көлем сияты геометриялық шамалар жөніндегі ұғымдар қалыптасты. Адамдар бірте-бірте кейбір қарапайым заңдылықтарды ашатындай дәрежеге көтерілді. Қисық жолға түзу жолдың төте екенін аңғару қиын болмады. Осылайша алғашқы геометрияның теориялары дұниеге келді. Бірақ бұларды ешкім дәлелдемеді. Дәлелдеуді керекте етпеді. Өйткені бұл теориялар астарында күн сайын тұрмыста көбірет сыналатын шүба келтірмейтін шындық жатты.

Уақытты өлшеуді, түнде бағытты бағдарлау тәрізді әрекеттер аспан шырақтарының қозғалысын жүйелі түрде бақылауды қажет етті. Бұл әрекет бұрынғыларды өлшеудің аспан сферасында орын алатын саласын қалыптастырды. Фигураларды зертеп білудің бастамалары еді.

3. Ғылым мен мәденетті ң барлық саласында өшпес мұра қалдыратын ежелгі герек ғалымдары (б.з 2000-2500 жылдар бұрын өмір сүрген ) өздерін ежелгі шығыс ғұламаларының шәкіртері санаған, олар әсіресе Мысыр және Вавилон сияқты шығыстың көне елінде жасалған миростардан үлгі , тәлім алып отырған. Геректердің астрономиялық білімдерінің де бастамалары ежелгі Вавилон астрономиялық еңбектерінде жатыр. Геректердің ұлы астрономиялары Гиппарх, Птоломейдің өздері ескі Вавилонда дүргізген астрономияық бақлаудың нәтижесін есте алы отырған. Египет, Вавилон елдері мәдениеті өте ертеде дамыған тарихи жұрттар қатарына жатады. Мысырдың бізге ғылыми, тарихи және басқа жақтарын жазылған көптеген попирусты хаттар келді (өсімдіктен жасалған төзімді жазу құралы - папирус). Ал Вавилондықтардың бізге мыңдаған сына жазулар (гленопистер) қалды. Олар жазулар мен есептерді арнайы дайындаған балшық тақталарға сына арқылы жазып ұзақ сақталу үшін оларды отқа күйдірген. Мысыр бұдан 4 мың жылдай бұрын біріккен қуатты мемлекет болып түрды. Осы кезде құрылыс аса күшті қарқынмен жүреді. Жер үдей қажеттігі күшейді, теңізден жүзіп тарихи экономиканың саяси байланыс жасаудың қажеттігі туады. Осы айтылғандардың бәрі ғылыми білімдерді көптеп қажет етіп, ғылымның шығуына дамуына қалайды әсер етеді. Сондықтан да мысырлықтар жаратылыстану, математика жөніндегі білімдерді жинақтап меңгеруге көрнекті табыстарға жетеді. Мысалы сүмбіле жұлдызының орның батып тууын зерттей келіп олар 1 жылда 365 күн бар екенің аңғарады. Осы кезде Мысыр күн парағы жасалады, Мысырлықтан соғатын кейіннең су сағатын жасады. Олар математика фактілердің, әдістердің жиналып қалдыруына әсер етті. Осы кезде Мысырмен қатар шығыстың екінші бір жерінде Вавилон мәдениеті гүлденіп тұрды. Вавилон – эфпрат және тигр өзендері арасынан қоныс тепкен азияның өте ескі мемлекеттерінің бірі болатын. (шамамен қазіргі Ирак мемлекетінің териториясы) Мысыр мен Вавилон елдерінең қалған бай білім мен өнер дәстүрлері кейіннең батыс пен шығыс елдерінде ежелгі грециядағы ғылым тууына өркендеуіне игі әсер етті. Бастапқы ірге тас болып қаланды.
4. Ежелгі Мысырлықтардың математика білім дәрежесінің айқындауы білетіндей екі папирус сақталған. Олардың біріншісі Римдік папирус Лондонда британ музейінде, ал екіншісі Москва папирусы Москвада. А.С Пушкинде сақталған. Біріншісінің өлшемі 55м х 32см 85 есеп жазылған. Екіншісі 5,5м 8см 25 есеп жазылған.бұлардың жазылу кезі б.з. 2000 жылдай бұрын папирустарда келтірілетін есептер қысқа догмолық түрде берілген жоғарыда айтылған папарустарды мұқият зерттеу тек өткен ғасырлардан айтылған. Бұл тұрғыда математика тарихын зерттеушілер елеулі жұмыстар енгізді. Ежелгі мысырда қазіргі қолданылып жрген позициялық емес рим нөмерлеуіне ұқсас ироглифтік ондық жүйе қолданылған. Мысырлықтан бір таяқша онды П (кісен), жүзді – с (өлшеуіш жіп), мыңды - ÷ (гүл жапырақ) деп белгілеген. Мысалы 2344 саның былай жазған ÷ ÷ с с с П П П П 1 1 1 1. Мысырлықтар төрт амалды бүтін сандарға, бөлшек сандарға да қолдана білген. Мысырлықтың кейбір арифметикалық есептерін шешу жолын қарастыра келіп, матаматика тарихшылары олар бір белгіс бар теңдеулерді шеше білген деген қортындыға келіп отыр.

Үймек және оның төрттен бірі он бес деген есеп, қазіргі біздің жазуымыз бойынша түріндегі теңдеулер келеді.

Мысырлықтар геометрия саласында едәуір жетістікке жеткенін байқаймыз. Олар үшбұрыш, квадрат, трапеция ауданын дұрыс формулалар арқылы табады, дөңгелектердің ауданын жуық түрде диаметрінің тоғыздан сегізінің квадратына тең деп алады. Олай болса, шеңбер ұзындықтарының оның диаматріне қатынасын көрсететін π саны үшін мынадай жуық мән табылады. бұл өз уақытымен салыстырғанда үлкен жетістік еді. Мысырлықтар қабырғалары, 3, 4,5 өлшем болып келетін үшбұрыштың тікбұрышты екенін білген. Олар осы үшбұрыш арқылы жер бетінде тікбұрыш салатын болған. Олар кубтың, паралепипедтің, дөңгелек цилиндр көлемін таба білген.
5. Вававилон математикасы жөніндегі негізгі деректерді біз олардан мириас болып қалған сына жазуынан қалғанын білеміз. Өткен ғасырда ежелгі ассерия патшасы акниезбанипалдық кітапханасы табылды. Математика тарихшылары математика тарихы үшін аса маңызды құжаттарды аудырып, жарыққа шығарды.

Вавилондықтар санаудың алпыстық жүйесін қолданды. Бұл жүйе бойынша барлық бүтін сан және бөлшек сандар мына тәріздес екі саннан өрнектелген бір үшін- , ал он үш- таңбасы қолданылады. Мысалы 34 саны .

Санаудың алпыстық жүйесін грек оқымыстылары қабылдады, олар арқылы бізге жетті. Уақыт және бұрышты өлшеу проблемалары да атап айтқанда, бір градус – алпыс минут, бір минут – алпыс секунд деген сияқтыларды, біз күні бүгінге дейін сол Вавилондықтардан пайдаланып келеміз.

Вавилондықтар Мысырлықтар сияқты көбейтуді қосуға және екі еселеуге келтірмей-ақ бірден жүргізді. Мұнда 2х2ден 59х59 дейінгі сандардың көбейтіндісін жатқа білуге тиісті болған. Дайын кесте пайдаланған. Бізге белгілі 300 математикалық тақташалар 200-ге жуығы осындай кестелерге арналған. Вавилон математиктері санның жуық квадрат түбірін табу кезінде формуласына пара-пар ереже қолданды. Бұл айтылғандардан Вавилондықтардан есептеу техникасының едәуір кемелденгенін көреміз. Мұндай жетілген есептеу жүйесінің болуы орларда алгебралық бөлім дағдыларының пайда болуына, молайуына әкеліп соқты. Олар бір белгісі бар теңдеулерді, квадрат теңдеулері және олардың жүйелерін шеше білген. Вавилондықтардың квадрат теңдеуін шешу жолы қазіргі біз қолданып жүрген формуламен пара-пар, сонымен қатар , , формуланың және арифметикалық прогрессияның қосындысын табу ережесін білген.

1945 жылы Вавилондықтардан қалған тағы бір математикалық текстінің мазмұны анықталды. Мұнда қабырғалары рационал сандар болып келген тікбұрышты үшбұрыш болып келген тізім келтіріледі теңдеуін қанағаттандыратын Пифагор. Сондықтан табу жолдарын қарастырған.

Пифагордан көп бұрын Вавилон математиктеріне «пифагор теоремасы» белгілі болды. Вавилондықтар үшбұрыштардың тіктөртбұрыш, трапеция аудандарын, призма мен цилиндр көлемдерінің дәл табу тәсілдерін білген т.б.

Осы шолудан біздің жыл санауымыздан 3000-6000 жылдар бұрын-ақ Мысыр және Вавилон елдерінде әр-түрлі санау жүйелеріне арифметикалық амал қолдану римше 1 және 2 дәрежелі теңдеулерді олардың жүйе шешу, аудан, көлем есептеу т.б. есептер шығарудың әдістерін жасау сияқты көптеген нақты матаматикалық мазмұндардың білім дағдылардың жинақталғанын көреміз.