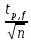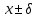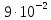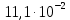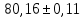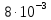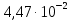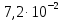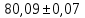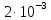аналитика практика. Практикалық сабақ №6. 6 Практикалы саба Санды анализ пнi жне дiстерi. Гравиметриялы талдау дісі
 Скачать 1.73 Mb. Скачать 1.73 Mb.
|
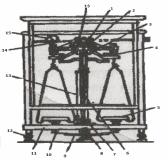
№6 Практикалық сабақСандық анализ пәнi және әдiстерi. Гравиметриялық талдау әдісіСандық анализ пәні – заттың сандық құрамын анықтауға мүмкіндік туғызатын әдістерді оқып үйрену. Сандық анализдің мақсаты – анализденетін заттың құрамына кіретін әр түрлі компоненттердің мөлшерін, сондай-ақ анализденетін қоспаның құрам бөліктерінің мөлшерлік арақатынасын анықтау болып табылады. Сандық анализ көмегімен көптеген мәселелер шешіледі, олардың негізгілері мыналар: Заттардың атомдық, мольдік және эквиваленттік массаларын анықтайды. Зерттелетін заттар құрамына кіретін иондар мен молекулалардың, элементтердің мөлшерін анықтайды. Зерттелетін затта оның құрам бөліктері қандай арақатынаста болатынын табады. Мөлшерлік анализдің мәліметтері бойынша, құрамындағы негізгі компоненттер мен қоспаның мөлшеріне байланысты болатын заттардың сапасын анықтайды. Бұл өз кезегінде заттардың қолдануға жарамдылығын анықтауға мүмкіндік береді. Мөлшерлік анализ көмегімен тұрақты химиялық бақылау арқылы өндірістегі технологиялық процестердің жүргізілу дұрыстығын тексереді. Химиялық бақылаусыз өндіріске материалдың ешқайсысы түспейді және дайын өнімнің ешқайсысы шықпайды. Мөлшерлік анализдің нәтижелері массалық үлеспен (%), бір литр ерітіндідегі моль санымен, 1 кг еріткіштегі моль санымен және т.б. көрсетіледі. Мөлшерлік анализді химиялық, сондай-ақ аспаптық әдіспен орындайды. Мөлшерлік анализдің химиялық әдістері құрам тұрақтылық заңына, зат массасының сақталу заңына, эквиваленттер заңына негізделген. Анализдің химиялық әдістеріне гравиметриялық және титриметриялық әдістер кіреді (қышқылды-негіздік, тотығу-тотықсыздану, комплексиметриялық, тұндыра титрлеу). Гравиметриялық анализ – құрамы анық белгілі қосылыс түрінде немесе химиялық таза күйінде бөлінген анықталатын компоненттің массасын дәл өлшеуге негізделген мөлшерлік анализ әдісі. Титриметриялық анализ – анықталатын заттың берілген мөлшерімен әрекеттесуге жұмсалған нақты концентрациялы реактив ерітіндісінің көлемін өлшеуге негізделген мөлшерлік анализ әдісі. Титриметриялық анализ негізінде эквиваленттер заңы жатыр. Титриметриялық анализге қарағанда, гравиметриялық анализ дәлірек болып табылады. Гравиметриялық анализде анықтау қателігі 0,1-0,005%, ал титриметриялықта – 0,1-0,05% болады. Бірақ гравиметриялық анализ ұзағырақ орындалады (бірнеше сағаттан бірнеше тәулікке дейін). Гравиметриялық анализге қарағанда, титриметриялық анализдің артықшылығы анализді өте жылдам орындау (экспрестігі) болып табылады. Гравиметриялық және титриметриялық әдістер аналитикалық химияның классикалық әдістері болып табылады, олар ғылыми зерттеулерде, заводтың лабораториясының тәжірибесінде жан-жақты қолданылады. Оларды тамақ өндірісінің технологиялық бақылауында: өнімдердің зольдігін (күлдігін) және ылғалдығын, қышқылдығын, қант мөлшерін, белокты, күкіртті қышқылды, судың кермектігін және т.б. анықтау үшін кеңінен пайдаланады. Мөлшерлік анализдің маңызды операцияларының бірі – аналитикалық таразыда жүргізілетін массаны өлшеу болып табылады. 1. Аналитикалық таразы Қазіргі уақытта химиялық анализде қолданылатын ең қажетті және ең дәл өлшегіш аспап – аналитикалық таразы. Химиялық анализде таразының бес түрі қолданылады: Технологиялық (техникалық) таразыны заттар мен нәрселерді 1 кг-ға дейін 0,01 г дәлдікпен жуықтап өлшеуге пайдаланады. Аналитикалық таразыны шекті жүгі 200 г дейінгі 0,0001 г дәлдікпен. Жартылай микроаналитикалық таразы шекті жүгі 100 г және 0,01 мг дәлдікпен. Микроаналитикалық таразы шекті жүгі 20 г және 0,0001 мг дәлдікпен. Ультромикротаразы шекті жүгі 1 г және 0,000001 мг дәлдікпен. Аталған аналитикалық таразылардың түрлерін бір табақты және екі табақты деп бөледі. Екі табақты (рычагты) аналитикалық таразының технохимиялықпен бірге жұмысшы (негізгі) бөлшектері бірдей болады, олар тек қана размерлерімен, детальдарының даярлану дәлдігімен және кейбір қосымша тетіктерімен, демек өлшеудің дәлдігі және жылдамдығымен, шекті жүгімен ерекшеленеді. АВ-200 аналитикалық таразысы. Таразы шыны футляр ішіне жинақталған, оның екі жағындағы есіктері ашылады және алдыңғы қабырғасы көтеріледі (1-сурет). Олар тең иінді рычаг болып келетін (1) күйентеден тұрады, күйентенің ортасына қырлары төмен қаратылған металл немесе агат призма (2) орнатылған. Ол (3) тірек бағанасына қатысты күйентенің тірек нүктесі болып табылады. Күйентенің ұштарына дәл осындай призмалар орнатылған, олардың бір қыры жоғары қаратылған. Осы призмаларға (4) ілмешектер арқылы (5) таразы табақтары ілінген. Күйентенің ортасына ұзын тігінен вертикаль (6) бағдарша орнатылған, оның төменгі ұшы таразы тербелгенде (7) бөліктерге бөлінген шкала бойлай қозғалады. Шкала орталығында нөлдік бөлік, ал екі жағында он-оннан бөлінген бөліктері бар. Таразының қажалатын бөліктерін (призмалар мен тірек аудандары) қажалудан сақтау үшін, таразыны (8) арретирмен қамтамасыз етеді, яғни таразының күйентесін көтеріп және оны тыныштық күйге әкелетін тетік. Таразының екі табағының астына да (9) рычаг көмегімен табақ тежегіштері (10) қойылады. Олар табақтардың тербелісін тоқтатады. Күйентенің (2) орталық призмасы және таразы табақтары көтеріліп тұрғанда, таразы жұмыссыз жағдайда, яғни арретирленген болады.
Өлшенетін нәрселерді және таразы тастарды тек қана арретирленген таразыға алып, салуға болады. Таразыны жұмыс жағдайына келтіру үшін арретирді сол қолмен жайлап сағат тіліне қарсы шегіне дейін төмен түсіру керек. Арретирленбеген және жүктелмеген таразы дұрыс жұмыс істегенде бағдарша шкала бойынша орталықтан (нөлдік) орын алуы қажет. Бағдаршаны шкаланың ортасында тұрақтандыру үшін күйентенің екі басында да екі гайка (14), кейде таразы күйентесінің ортасында бұл мақсатқа бір «шағала» (чайка) болады. Өлшенетін зат пен тастардың теңестірілгенін тексеру үшін де арретирдің тұтқасын жайлап сағат тіліне қарсы төмен бұру керек (тыныштық жағдайда тілі шкаланың нөлімен сәйкес келеді). Вертикаль тіреу колонкасы орнатылған (11) төменгі тұғырық, (12) тұрақтандыратын винтке және аяғына тіреледі. Осы винттерді айналдырып таразыны вертикаль жағдайға алып келеміз. Таразының тіреу бағанасының (колонка) горизонталь орнығуының дұрыстығын анықтау үшін ұшталған гірге ұқсайтын ұзынша келген жіпке ілінген тіктеуіш не деңгей (13) қолданылады. Осы гірдің астына жоғары қаратып қозғалмайтын тұғырға сүйір ұш орнатылған. Егер тіктеуіштің (гірдің) сүйір ұшы қозғалмайтын сүйір ұштың дәл үстінде тұрса, таразы дұрыс орнатылған (тіктеуіш бойынша). 2. Мөлшерлік анализдегі есептеу ережелері Химиялық анализ жасағанда есептеулерді өте мұқият жүргізу керек. Сан мәнінен жіберілген математикалық қате, анализде жіберілген қатемен пара-пар. Сан мәні дәл және жуықтап алынған деп бөлуге болады. Дәл алынғандарға, мысалы орындалған анықтаулардың санын, элементтің периодтық жүйедегі рет нөмірін жатқызамыз. Жуықтап алынған сандарға, мысалы, мөлшерлік анализдегі ерітінді көлемін немесе заттың массасын өлшеу жатады. Жуықтап алынған санның дәлдігі мәнді цифлар мөлшерімен немесе ондық белгілер санымен анықталады. Жуықтап алынған сандардың мәнді цифрлары деп үтірдің сол жағында тұрған, нөлден басқа цифрлары және үтірден кейін оң жағында тұрған нөлдерден басқаларын атайды. Санның ортасында тұрған нөлдер мәнді цифрлар болып табылады. Мысалы, 427,205 санында мәнді цифрлар алтау, 0,00365 – үшеу, 244,00 – үшеу болады. Санның ондық белгілері деп үтірден оң жақта тұратын және оның бүтін бөлігін бөліп тұратын барлық цифрларды атайды. Мысалы, 49,204 санына үш, 235,00 – екі, 18,00365 – бес ондық белгі бар. Химиялық анализ жасағанда есептеулер дәлдігі ГОСТ-пен немесе ТЖ (техникалық жағдайлармен) анықталады. Талап етілетін дәлдікке сәйкес анализдің есептеген нәтижесінде мәнді цифрлардың немесе ондық белгілердің саны болуы қажет. Аналитикалық таразыда өлшегенде гравиметриялық анализде ондық белгілердің саны төртке тең (мысалы, тиглдің массасы 12,3618 г). Титриметриялық анализде ерітіндінің көлемін бюреткамен өлшегенде дәлдігі екі ондық белгі (мысалы, 15,23 см3), ал концентрацияны есептегенде – төрт ондық белгісі (мысалы, 0,7512 моль) және т.с.с. болады. Егер есептеу үшін керек санның дәлдік дәрежесі үлкен, ал есептеудің дәлдік дәрежесі кемдеу талап етілетін болса, онда есептеудің нәтижесінде алынатынға қарағанда бір мәнді цифрға артық қалатындай етіп, барлық берілгендерді дөңгелектейді. Мысалы егер ГОСТ немесе ТЖ бойынша төрт мәнді цифр алу талап етілсе, 0,0274866 санын 0,027487-ге дейін дөңгелектейміз. Жуықтап алынған сандарды мына ереже бойынша дөңгелектейді: егер соңғы цифр бестен кіші болса, оны алып тастайды, егер ол тең немесе үлкен болса, онда соңғыдан алдыңғы алдыңғы цифрды бірге арттырады. Мысалы, екі сан бар: 0,86527 және 0,86534. Дөңгелектегенде сәйкес алатынымыз: 0,8653 және 0,8653. Анализ нәтижелерін есептегенде берілген өлшеу қандай дәлдікпен жүргізілетінін есепке алу қажет. Соңғы нәтижеде қосып және алғанда үтірден кейінгі белгілерді, шынайылығы аз санда болатындарынан артық болмайтындай етіп сақтайды. Мысалы, натрий хлоридінің мольдік массасын есептегенде натрий мен хлордың салыстырмалы атомдық массасын кестеден табады, (1-форзацты қара) натрийдікі – 22,9898, хлордікі – 35,453. Натрийдің салыстырмалы атомдық салмағы төртінші белгіге дейін, ал хлордікі – үшінші дәлдікке дейін берілгендіктен, натрийдің салыстырмалы атомдық массасын үшінші белгіге дейінгі дәлдікпен есептейді. NaCl мольдік массасы 58,442 г/моль тең болады. Есептеулерді тездету үшін микроколькуляторларды пайдалану ұсынылады, мұнда аталған ережелерге сай барлық нәтижелерді дөңгелектеу керек (аралық және соңғыларын да). Егер есептеулердің дәлдік дәрежесі жоғары болса, онда нәтиженің алдына = (теңдік) белгісін, ал дәлдігі кем болғанда теңдік белгісінің орнына ≈ (шамамен тең) белгісін қояды. Айтылған ережелерді ескермей жасалған есептеулер дұрыс деп саналмайды. 3. Метрологиялық сипаттамалар Дұрыстық, қайталанғыштық және дәлдік Кез келген мөлшерлік анықтаудағы негізгі талап татпадағы элементтердің ақиқат мөлшерін бейнелейтіндей эксперименттік (тәжірибелік) нәтижелер алудан, яғни осы нәтижелердің үлгі құрамына мүмкіндігінше дәлірек сәйкес келуінен тұрады. Күрделі үлгінің құрамын 100%-тік ықтималдықпен анықтау мүмкін емес. Алайда, үлгіні анализдеуді көп рет қайталай отырып, жуықтаудың жақсы дәрежесіне жетуге болады, сонда анализдің барлық операциялары методика талаптарының бәріне сәйкес мұқият және дұрыс орындалуы тиіс. Анализді сәйкес стандарт үлгілерді пайдаланып әр түрлі әдістермен жүргізу жасалған методиканың дұрыстығын бағалауға мүмкіндік береді. Анализдің дұрыстығы орташа және ақиқат нәтижелерінің арасындағы айырмашылықпен сипатталады. Анализдің дұрыстығы жүйелі қателіктерден толығымен арылудың сәті түскен кезде қамтамасыз етеді. Іс жүзінде анықтаудан анықтауға көшкенде эксперимент нәтижелері білудің қайсыбір интервалында өзгеріп отыратындықтан, анализ деректерін статистиканың қарапайым әдістерімен өңдеу қабылданған. Ол үшін жеткілікті түрде көп өлшеулер негізінде орташа мәнді табады да, нәтижелердің осы орташа мәнге қатысты шашырауын есептейді. Бұл шашырау анализ методикасының дәлдігін немесе қайталанғыштығын сипаттайды. Өлшемдердің қайталанғыштығы әр түрлі жағдайларда (әр түрлі уақытта және әр түрлі орындаушылар) жасаған өлшеулер нәтижелерінің бір-біріне жуықтығын білдіреді, талдау қайталанымды, бірақ дұрыс емес бола алатынын ескерген жөн. Өлшемдердің дәлдігі анықтаулар нәтижелерінің өлшенетін шаманың ақиқат мәніне жуықтығын бейнелейді. Анализдің дәлдігі дұрыстық ұғымымен де сипатталады. Дәлдік және қайталанғыштық ұғымдары бірін бірі толықтырады. Қайталанғыштық жоқ болғанда дәлдікке қол жету мүмкін емес, бірақ жақсы қайталанғыштық та жоғары дәлдікті бере алмайды. 4. Қателіктерді жіктеу ГОСТ 16263-70 бойынша «өлшеудің қатесі» терминін қолдану қабылданбаған, «өлшеудің қателігі» деген термин дұрыс деп есептеледі. Абсолютті қателік – талдау нәтижесінің өлшенетін шаманың ақиқат мәнінен ауытқуы: ∆хі = хі – μ (1) Мұндағы хі – анықтау нәтижесі, μ – талданатын компоненттің ақиқат мөлшері. Салыстырмалы қателік – өлшеудің абсолютті қателігінің ақиқат мәнге қатынасы: ∆хі / μ = (хі – μ) / μ немесе ∆хі / μ = 100% (хі – μ) / μ (2) Салыстырмалы қателік көбінесе процент арқылы өрнектеледі. Өлшеу қателігі көптеген факторларға байланысты, олар: реагенттердің, аналитикалық ыдыстың тазалығы; орындаушының өзіндік қабілеттілігі; өлшеу методикасы; химиялық және физикалық операциялар саны, пайдаланылатын ыдыс пен жабдықтардың (аппаратураның) дәлдік класы және т.б. Жүйелі қателік – өлшеудің әрдайым тұрақты болып қалатын немесе қайталанатын анализдерде заңдылық бойынша өзгеріп отыратын қателігін сипаттайды. Жүйелі қателік тұрақты таңбаға ие болады, яғни ол анализ нәтижесін тек арттырып немесе кемітіп отырады. Жүйелі қателіктер түзетулер енгізу, эталонмен салыстыру және басқа да тәсілдер арқылы есептеле (ескеріле) және елеулі түрде азайтыла алады. Өлшеудің кездейсоқ қателігі деп қайталанған өлшеулерде кездейсоқ сипатта өзгеретін қателік аталады. Оның таңбасы тұрақты емес, кездейсоқ түрде өзгеріп отырады. Өрескел қателіктер (оларды мүлт кетулер деп те атайды) тәжірибені қайталаған сайын елеулі түрде өзгеріп отырады. Олар аналитиктің оперативтік қателіктері нәтижесінен және пайдаланылатын жабдықтың (аппаратураның) кездейсоқ қателіктері салдарынан пайда болады. Тәжірибелік нәтижелерді өңдеу кезінде олар байқалуы және шығарып тасталуы тиіс. Анализдің нәтижелері дұрыс та қайталанғыш; қайталанғыш, бірақ дұрыс емес те, қайталанбайтын да бола алады. Бұл белгілер анықтаулардың алынған нәтижелерін метрологиялық өңдеу негізінде айқындалады. 5. Жүйелі қателіктер Жүйелі қателіктердің пайда болу көздері едәуір көп. Олардың ішінде ең маңыздылары – пайдаланылатын аспаптар мен реактивтерге байланысты қателіктер; әдістің қателіктері; орындалушының шеберлік дәрежесіне, кейбір тәуелділіктер мен заңдылықтарға немқұрайлы қарауға, ыдыстың, жабдықтың ластығына байланысты қателіктер. Аналитикаық тәжірибеде қолданылатын аспаптар белгілі бір дәлдік класымен сипатталады. Дәлдік класы жоғарырақ аспаптарды пайдаланғанда анықтаудың қателігін төмендете аламыз. Жүйелі қателіктер стандартталмаған таразыларды, мөлшері айқын белгіленбеген өлшеуіш ыдыстарды қолданудан, спектрофотометр призмасының ауытқуынан, фотоэлементтердің күңгірттігіне және т.б. себептерден пайда болады. Мысалы, стандарт үлгілер бойынша мөлшерлік деңгейлерді белгілегенде анықталатын түзетулерді енгізу немесе алынған нәтижелерді дәлдік класы жоғарылау болатын басқа аспаптардың көрсетулерімен салыстыру арқылы бұл қателіктерді өлшеуге және біршама ескеруге болады. Анықталатын элемент пен кедергі жасайтын қоспадан тұратын реактивті қолдану да жүйелі қателік туғызады. Реактивтерді алдын ала мұқият тазарту және кедергі жасайтын қоспаларды бөліп алу ол қателікті азайтады. Әдістің қателіктері талданатын жүйенің қасиеттеріне тәуелді: тұндыру немесе шаю кезінде тұнбаның ерігіштігі; қоспалардың қоса тұнуы; уақыт барысында фотометрленетін ерітінді тұрақсыздығы, реакция жүруінің толық еместігі және т.с.с. Методикалық қателіктер әр методикаға тән болғандықтан көбінесе байқалмай қалады. Анализ барысында орындалатын барлық операцияларға байланысты және негізінен анализ жасаушының шеберлігі мен оның қабілетіне тәуелді болатын оперативтік және өзіндік қателіктердің де елеулі маңызы бар. Егер аналитик мысалы, түрлі-түсті индикаторлармен титрлеу кезінде бояу түсінің өзгеруін дәл ажырата алмаса, онда ол ерітінділерді әрқашан не асыра, не жеткізбей титрлейді. Жүйелі қателіктерді байқау және оларды болдырмау анализ барысында мүмкін болатын бөгеттер мен жүйелі қателіктердің пайда болуы тұрғысынан барлық операцияларды сын көзбен бағалауға негізделеді. Сондай-ақ теріс түсініктер қателігін де атап өткен жөн. Олардың мәнісі мынада: қайталанатын анықтаулар кезінде аналитик көз мөлшерімен өлешегенде аспаптың тең ықтималды екі көрсетулерінің алдыңғы нәтижеге жуықтау болатындай мәнін таңдап алады. Әдетте, жүйелі қателіктер бірінші кезекте байқалуы және ескерілуі тиіс. Жүйелі қателіктерді байқаудың ең көп тараған тәжірибелік тәсілдері – анализді бір-бірінен тәуелсіз әдістер арқылы орындау, құрғақ (бақылау мақсатымен) тәжірибе жүргізу және стандарт үлгілерді қоса (параллель) анализ жасау болып табылады. Стандарт үлгілер деп құрамындағы анықталатын элементтердің мөлшері жоғары дәрежелі дәлдікпен белгілі болатындай әр түрлі материалдар аталады. Оларды градуирленген графиктерді салу, анализді үстемелер әдісімен жүргізу және осылайша заттың құрамын анықтау үшін әр түрлі аналитикалық әдістерде, сондай-ақ анализдің дұрыстығын тексеру, әр түрлі методикаларды шынайы метрологиялық сипаттау және т.с.с. үшін қолданады. Стандарт үлгілерге бірқатар талаптар қойылады. Олар үшін аса маңыздыларын аиап өтейік. Эталондалған элементтердің мөлшері реттелген және көрсетілген қателіктер аралығында ақиқат мөлшерден аспауы тиіс. Стандарт үлгінің құрамы барлық немесе кейбір анықталатын компоненттер бойынша арнайы куәлікпен (паспортпен) расталады. Ұзақ уақыт сақтау кезінде стандарт үлгінің құрамы өзгермеуі тиіс. Ол бүкіл массасы бойынша анализ жасау үшін татпалар таңдаудың тепе-теңдігін қамтамасыз ететіндей химиялық құрамының жоғары біртектілігіне ие болуы керек. Әдетте ол біртұтас үлгі ұсақ металл жоңқалары, ұнтақтары және т.с.с. Стандарт үлгілердегі эталондалатын элементтердің мөлшері өндірістік үлгілердегі сол элементтердің анықталу дәлдігінен әлдеқайда артық болатындай дәлдікпен тағайындалады. Идеал эталон тек анықталатын элементтің мөлшерімен ғана татпалардан ерекшеленуі тиіс. Бұл талап іс жүзінде орындалмайды, сондықтан әдетте татпалар мен эталондар құрамындағы айырмашылық кездейсоқ қателіктерден асып кететін жүйелі қателіктер тудырмайтындай болуын талап етумен шектеледі. Стандарт үлгілердің талдауын өте шебер аналитиктер әр түрлі әдістерді пайдаланып жүргізеді. Бізде стандарт үлгілерді ғылыми-зерттеу орталығы (Свердловск қаласы) бар стандарт үлгілердің мемлекеттік қызметі ұйымдастырылған, мемлекеттік тізімге 500-ден астам сапасы кепілдендірілген стандарт үлгілер енгізілген. Қара және түрлі-түсті металдар құймаларының әр түрлі топтары үшін сенімді эталондар бар. Рудалар, минералдар, тау кендерін және т.с.с. анализ жасау үшін эталондар дайындау әлдеқайда күрделірек, өйткені бұл материалдар біртекті емес және олардың құрамдары әр түрлі болады. Кездейсоқ қателіктер Кездейсоқ қателіктердің анықталған таңбасы болмайды және «кездейсоқ» деген атаудың өзі бұл қателіктердің пайда болуында қандай да бір заңдылықтың жоқ екенін білдіреді. Кездейсоқ қателіктердің бар болуы тіпті жүйелі қателіктер шығу көздерінің бәрі сәйкес түзетулер көмегімен ескерілген күннің өзінде параллель анализдердің нәтижелері бір-бірінен әрқашан дерлік біршама өзгеше болуымен байқалады. Кездейсоқ қателіктердің пайда болуы әдетте кездейсоқ оқиға ретінде қарастырылады да, бұл қателіктер ықтималдықтар мен математикалық статистика теориясы негізінде өңделеді. 6. Анализ нәтижелерін статистикалық өңдеу Қателіктер теориясында егер қателіктер Гаусстың үлестіру заңына сәйкес болса, онда өлшенетін шаманың ең ықтимал және сенімді өлшеулердің алынған теңаралықты мәндерінің математикалық үміті немесе олардың арифметикалық орташасы болатыны тұжырымдалады. Бұл берілген шартта орындалуы мүмкін болатын бақылаулардың бәріне, жиынтығына қатысты. Осы бақылау нәтижелерінің арифметикалық орташасы μ сара (генеральдық) орташа деп аталады. Аналитикалық химияда параллель анықтаулар саны әдетте көп емес және алынған нәтижелер жиынтығын таңдамалық жиынтық немесе кездейсоқ таңдама деп атайды. Кездейсоқ таңдаманың орташа мәні таңдамалық орташа деп аталады. Статистикалық анализ әдістерімен кездейсоқ таңдама нәтижелері бойынша сара жиынтықтың параметрлерін бағалауға және сонымен татпадағы компонент мөлшерінің ең ықтимал мәнін табуға болады. Таңдамалы жиынтықтан алынған бірлік анықтаудың сандық мәнін варианта деп атайды да хі арқылы белгілейді. Варианталардың қайсыбір саны, яғни татпадағы компонентті бір ғана әдіспен параллель анықтаулардың нәтижелері хі, хі ... хn осы варианталар жиынтығын құрайды. Варианталар саны n-ға бөлінген варианталардың қосындысын орташа немесе арифметикалық орташа деп атайды: 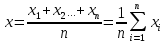 (3) (3)Жеке нәтиже мен орташа мәннің арасындағы айырым кездейсоқ ауытқу немесе бірлік ауытқу, немесе жай ғана ауытқу болады да d немесе ∆ арқылы белгіленеді di = хі - 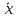 (4) (4) Жеке анықтаудың таңдамалық стандарт ауытқуын формуласымен есептейді: 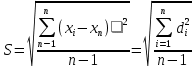 (5) (5) Стандарт ауытқудың квадратын дисперсия деп атайды: 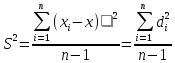 (6) (6)Егер бақылаулар саны өте көп болса, онда S шамасы қайсыбір тұрақты σ мәніне ұмтылады, ол мәнді S статистикалық шегі деп атаймыз: σ = lim S (7) Қатаң түрде айтқанда, дәл осы шекті стандарт ауытқу, ал оның квадратын өлшеулердің дисперсиясы деп атаған жөн. Сонымен, аналитикалық анықтау шарттарында әдетте сара орташа μ-ді емес, таңдамалық орташа х-ты, σ-ды емес, стандарт таңдамалық ауытқу S-ты табады. Қайталанымдықты бағалау үшін орташа мәннің таңдамалық дисперсиясын 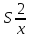 : :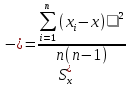 (8) (8)және орташа нәтиженің стандарт ауытқуын есептейді. 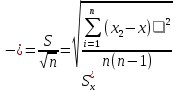 (9) (9)Есептеулер μ=-σ-дан μ=+σ-ға дейінгі аралықтағы интеграл үлестіру қисығымен және абсциссалар осімен шектелген жалпы ауданның (10.1-сурет) 68,3%-ін, μ=-2σ-дан μ=+σ-ға дейінгі аралықта - 95%-ін, μ=-3σ-дан μ=+3σ-ға дейінгі аралықта – 99,7%-ін құрайтынын көрсетеді. 10.1.-суретте штрихталған ауданға тең интеграл көрсетілген мәндер аймағында (х= - Rσ-дан (х=+kσ-ға дейін)) х1 нәтижесінің пайда болу Р ықтималдығын білдіреді. Ықтималдықтың бұл шамасын сенімді ықтималдық немесе статистикалық сенімділік деп, μ=-kσ-дан μ=+kσ-ға дейінгі аралықты сенімділік интервалы деп, ал аралықтың шекараларын сенімділік шекаралары деп атайды. Сонымен, нәтижені μ=-kσ-дан μ=+kσ-ға дейінгі аралықта алудың сенімді ықтималдығы 68,3% яғни осы аралықта барлық нәтижелердің 2/3-дей бөлігі жатады деп айтуға болады (-2σ, +2σ), аралығының ішінде нәтижелердің 95%-ті, ал (-3σ, +3σ) аралығында – 99,7%-ті яғни іс жүзінде нәтижелердің бәрі жатады. Интегралдау шектерінен тыс жататын талдау нәтижелерін алудың ықтималдығы: 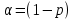 –ға тең (10) –ға тең (10)Бұл шаманы мәнділік деңгейі деп атайды. Қалыпты, (нормаль) үйлестірілуге негізделген қателіктердің классикалық теориясы бір шаманың өлшеулері көп рет орындалатындай астрономияда, геодезияда және басқа да салаларда кеңінен қолданылады. Алайда заттың мөлшерлік анализі бойынша деректерді өңдеу негізінде ол жеткілікті түрде тиімді болмайды, өйткені ол әдетте қателіктердің төмендетілген нәтижелерін береді. Шынында да, қалыпты үлестірілу заңына сәйкес шағын қателіктердің пайда болу ықтималдығы үлкен қателіктердің пайда болу ықтималдығына қарағанда көп, сондықтан бақылаулардың (параллель татпалар) саны аз болғанда үлкен қателіктер әдетте пайда болмайды, бұл азғана нәтижелерді қалыпты үйлестірілуге сәйкес өңдегенде қателіктердің төмендеуіне әкеледі. Шағын таңдамалар статистикасын пайдаланған кезде қателіктің дәлірек шамасы алынады. Бұл статистика ХХ ғасырдың басынан дамып келеді, ол t үлестіру немесе Стьюдент-Фишер үлестірілуі деп аталады.
Стьюдент-Фишер үлестірілуі Өлшеулердің шектелген саны үшін берілген шама анықталған x = tp Sx сенімді ықтималдығымен іске асырылады, (10.11) мұндағы tp – Стьюдент коэффициенті, ол n мен P мәндері үшін есептелген t үлестірілуден табылады да, жуықталады. Өлшеулер саны көп (n>20) болғанда t үлестірілу қалыпты үлестірілуге жақындайды. Стьюдент коэффициенттері 10.1-кестеде келтірілген, онда еркіндік дәрежесі f = n-1. Өлшеулердің шектелген санында t үлестірілу мен Гаусстың қалыпты үлестіруі арасындағы айырма едәуір елеулі болады, мысалы, f = 3 және P = 95% (0,95) үшін t коэффициенті 3,18-ге тең, ал қалыпты үйлестірілу мәні 2-ге тең болу керек еді. Бұл анықтаулар (параллель татпалар) саны аз болумен түсіндіріледі, бұл жағдайда t-үлестірілу қатаңырақ есептеледі.
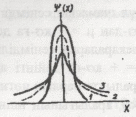
Қалыпты үлестіру сияқты t – үлестірілу де абсциссаның сол мәнінде симметриялық максимумға ие болады, алайда қисықтың биіктігі мен ені сияқты сипаттамалары өлшеулер санына тәуелді (2-сурет). Берілген сенімді P ықтималдығы мәнінде нәтиже жататындай сенімділік интервалы: 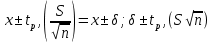 (11) (11)f → ∞ жағдайда t – үлестірілу қалыпты үлестірілуге көшеді де олардың арасындағы айырма іс жүзінде f = 20 болғанда білінбейді. Статистикалық өңдеу мысалы Әк тас құрамындағы кальций мөлшеріне комплексонометриялық әдіспен анализ жасау кезінде – аналитик массадағы Са-дің проценттік мөлшері 80, 15; 80, 28; 80, 05, 80, 20, 80, 10 және 78, 40 екенін анықтады. 2-аналитик дәл сол үлгіні гравиметриялық әдіспен талдау жасап, келесі нәтижелерді алды: 80, 10; 80, 06; 80, 08 және 80, 12. Бұл жағдайда нәтижелердің дұрыстығын қалай бағалау керек? Бәрінен бұрын айқын түрде кішірейген мәні бар (78,40%) 1-аналитиктің соңғы нәтижесі көзге түседі. Оны өрескел қателікке жатқызып қарастырудан шығарып тастау керек. Берілген жағдайда небары бес вариантадан (n=5) тұратын шағын таңдама бар. 1-аналитик үшін Са құрамы жайлы басқа әдістермен табылған деректер жоқ, сондай-ақ әк таста (μ) Са құрамының нақты мәні ретінде қабылдауға болатындай нәтижелер де жоқ. Бұндай жағдайда тәжірибеші (эксперименттеуші) өз нәтижелерінің дұрыстығын бағалауда өзінің шектелгендігін түсінуі керек, бірақ ол әк таста Са құрамын анықтау әдісінің дұрыстығы мен қайталанғыштығын бағалай білуі тиіс. Қайталанғыштықты бағалау үшін стандарт ауытқудың (S немесе δ) дисперция (S2) шамасын есептейді. Алдын ала х орташа мәнін есептейді. 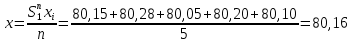 Содан кейін анализдің әрбір нәтижесінің орташа мәннен ауытқуын есептейді, олар сәйкес: 0,01; 0,12; 0,11; 0,04; 0,06. Стандарт ауытқуды (10.5) формуласы бойынша есептейді: 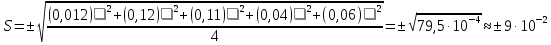 Шындық мән (μ) ретінде қабылдауға болатындай кальций құрамының мәні белгісіз және ол шамаға жуықтықтың дұрыстығын бағалау мүмкін емес болғандықтан, сенімділік интервалын δ, яғни ақиқат орташа мәннің табылуын берілген ықтималдық дәрежесімен күтуге болатындай аймақты анықтау қажет. Әдетте ықтималдықты 0,95 (немесе 95%) деп қабылдайды, бұл 100-ден 95 дұрыс нәтиже сенімділік интервалында (+δ) жататынын білдіреді. Мұны 10.12-формуламен есептейді. Кесте бойынша алдын ала мәндерін t – критериі үшін табады (мысалы, 10.1-кестеден), ол n = 5 және f = n-1 = 4 болғанда 2,78-ге тең. Жүргізілген есептеулер нәтижелері гравиметриялық әдіс бойынша есептелген нәтижелермен бірге 10.2-кестеде келтірілген, бұлар анализден алынған нәтижелерді дұрыс деп санауға болатынын көрсетеді. 1-кесте Стьюдент коэффициенттері
2-кесте Тәжірибе нәтижелерін статистикалық өңдеу
3-кесте P = 0,95 болғандағы F – критерий
4-кесте Q сандық мәндері
Бұдан әдістің қайталанғыш екені және ақиқат орташа едәуір шағын сенімділік интервалында жататыны шығады. Жүйелі қателіктердің болуы мұнда байқалмайды. Нәтиже дұрыстығын едәуір қатаңырақ бағалау үшін және жүйелі қателіктерді анықтау үшін әк тасты анализ жасаудың жүйелі қателігі жоқ екені алдын ала белгілі, мұны CaC2O4  2H2O түріндегі гравиметриялық тұндыру сияқты тәуелсіз әдіспен орындау керек (2-аналитиктің нәтижелері). Гравиметриялық әдіс нәтижелерінің статистикалық өңдеу тізбегі сақталады. Алайда комплексонометриялық әдіс нәтижелерінің дұрыстығын бағалағанда орташа мәндері Фишер критериі (F-критериі) бойынша салыстыру керек. 2H2O түріндегі гравиметриялық тұндыру сияқты тәуелсіз әдіспен орындау керек (2-аналитиктің нәтижелері). Гравиметриялық әдіс нәтижелерінің статистикалық өңдеу тізбегі сақталады. Алайда комплексонометриялық әдіс нәтижелерінің дұрыстығын бағалағанда орташа мәндері Фишер критериі (F-критериі) бойынша салыстыру керек.Екі әдістің (комплексонометриялық және гравиметриялық) дисперсияның тәжірибелік жолмен табылған қатынасы: 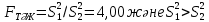 Бұл нәтиже сәйкес екендігін дәрежелері мен мәнділік деңгейі үшін (Fкесте =9.12) салыстырмалы (3-кесте). Егер FТӘЖ < Fкесте болса, онда екі әдістің орташа мәндері арасындағы айырма елеусіз болады да екі әдістің нәтижелерін бір таңдамаға біріктіру мүмкіндігі бар. Егерде FТӘЖ < Fкесте болса, онда әдістің сондай орташа мәндері арасындағы айырма елеулі болар еді де, әдістердің нәтижелерін бұл жағдайда бір таңдамаға біріктіру мүмкін емес, яғни тексеретін әдісте жүйелі қателіктер орын алады. Біздің мысалда таңдаманың дисперсиялары комплексонометриялық және гравиметриялық анықтаулар үшін сәйкес 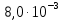 және және 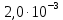 екі дисперсиялық: қатынасы екі дисперсиялық: қатынасы 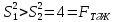 . Еркіндік дәрежелер саны f1 = n1-1 = 4 дисперсиясы . Еркіндік дәрежелер саны f1 = n1-1 = 4 дисперсиясы 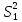 үлкен таңдама үшін (комплексонометриялық анықтау), ал үлкен таңдама үшін (комплексонометриялық анықтау), ал 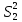 дисперсиясы кіші таңдама үшін f2 =3 (гравиметриялық анықтау). Мәнділік деңгей: 0,05 болғанда сәйкес еркіндік дәрежелері үшін Фишер критериінің кестелік мәні 9,1-ге тең, яғни FТӘЖ = 9,1. Біз FТӘЖ < Fкесте екенін алдық, демек, екі таңдаманың орташа мәндері арасындағы айырма елеусіз болады. Сонымен екі анықтаудың нәтижелерін бір таңдамаға біріктіруге болады және кальций құрамын анықтаудың комплексонометриялық әдісі берілген дәрежелі дәлдігімен мәнді жүйелі қателіктерден бос екенін білуге болады. Шынында да, гравиметриялық анықтаудың орташа мәні 80,90% комплексонометриялық анықтау нәтижелерінің 80,05%-80,27% сенімділік интервалына, ал оның орташа мәні 80,16% гравиметриялық анықтау нәтижелерінің 80,09%-80,16% сенімділік интервалына тиісті. Жүргізілген статистикалық өңдеу комплексонометриялық әдістің жақсы қайталанымды (5-0,08%) және дұрыс әдіс екенін көрсетеді. дисперсиясы кіші таңдама үшін f2 =3 (гравиметриялық анықтау). Мәнділік деңгей: 0,05 болғанда сәйкес еркіндік дәрежелері үшін Фишер критериінің кестелік мәні 9,1-ге тең, яғни FТӘЖ = 9,1. Біз FТӘЖ < Fкесте екенін алдық, демек, екі таңдаманың орташа мәндері арасындағы айырма елеусіз болады. Сонымен екі анықтаудың нәтижелерін бір таңдамаға біріктіруге болады және кальций құрамын анықтаудың комплексонометриялық әдісі берілген дәрежелі дәлдігімен мәнді жүйелі қателіктерден бос екенін білуге болады. Шынында да, гравиметриялық анықтаудың орташа мәні 80,90% комплексонометриялық анықтау нәтижелерінің 80,05%-80,27% сенімділік интервалына, ал оның орташа мәні 80,16% гравиметриялық анықтау нәтижелерінің 80,09%-80,16% сенімділік интервалына тиісті. Жүргізілген статистикалық өңдеу комплексонометриялық әдістің жақсы қайталанымды (5-0,08%) және дұрыс әдіс екенін көрсетеді. Қателіктерді анықтау Методиканы жасағанда немесе едәуір жеткілікті дұрыс нәтижелер алуға ұмтылғанда аналитик бірнеше параллель анықтаулар жасайды, олардың кейбіреулері басқаларынан және бүкіл серияның орташа мәнінен мүлдем ерекше болады. Бұл нәтижелерді қалай болса солай алып тастау жеткілікті түрде қолайсыз, өйткені ол орташа арифметикалық мәнді есептеуге қате берілгендерді енгізу сияқты талдаудың жалпы нәтижесін елеулі түрде бұрмалауы мүмкін. Шамамен алғанда өрескел қателіктер деп 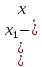 теңсіздігі сақталатындай, яғни орташа мәннен абсолют ауытқу жеке нәтиженің стандарт ауытқуы мәнінен үш еседен артық болатындай қателіктерді есептеуге болады. теңсіздігі сақталатындай, яғни орташа мәннен абсолют ауытқу жеке нәтиженің стандарт ауытқуы мәнінен үш еседен артық болатындай қателіктерді есептеуге болады. Егер тәжірибелер саны 10-нан көп болмаса, онда Q-критерийді пайдалану дұрысырақ. Бұл жағдайда алынған нәтижелерді шамаларының өсуі ретімен орналастырған тиімді: х1, х2, ... хn . Бірінші мен соңғы мәндердің арасындағы айырым варияциялау ауқымы деп аталады: R = хn - х1. Ең ықтимал жағдай – қатардың шеткі мәндері х1 мен х2 өрескел қателіктер болып шығуы, олар 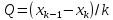 (13) (13)формуласымен анықталады, мұндағы 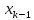 мен мен 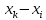 , х1, х2, ... хn қатарындағы көршілес мәндер. Осы формула бойынша есептелген Q-дың мәндерін берілген ықтималдық P- мен f еркіндік дәрежесі санындағы критерийдің Qкесте кестелік мәнімен салыстырады (мысалы, 10.4-кесте). Егер Q > Qкесте болса, онда анализдің күдікті нәтижесі өрескел қателік болады және оны орташа арифметикалық мәнді есептегенде шығарып тастау керек. , х1, х2, ... хn қатарындағы көршілес мәндер. Осы формула бойынша есептелген Q-дың мәндерін берілген ықтималдық P- мен f еркіндік дәрежесі санындағы критерийдің Qкесте кестелік мәнімен салыстырады (мысалы, 10.4-кесте). Егер Q > Qкесте болса, онда анализдің күдікті нәтижесі өрескел қателік болады және оны орташа арифметикалық мәнді есептегенде шығарып тастау керек.Солай әк тастағы кальцийді комплексонометриялық тәсілмен анықтаудың келтірілген мысалында анализ нәтижелерін қатарға былай орналастыруға болады: 78, 40; 80,05; 80,10; 80,15; 80,20; 80,28. Варияциялау ауқымы k = 80,28-78,40 = 1,88 болады. Анализдің бірінші нәтижесі үшін Q критерий мынаған тең: Q = (80,06-78,40) (1,88=1,65/1,88=0,88). P = 0,95 пен f=5 үшін кестелік мән Qкесте = 0,56, яғни Q > Qкесте. Демек берілген нәтиже өрескел қателік болады. Екінші және соңғы нәтижелер үшін Q критерий сәйкес: (80,10-80,05) 1,88-0,05/1,88 =0,027 және (80,28-80,20) 1,88 =0,08/1,88 =0,043. Бұл шамалар Qкесте мәнінен кіші және олар өрескел қателік болып есептелмейді. | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||