Навигация по странице:Не путать с тригонометрическим тангенсом, который является относительной и безразмерной величиной.Скорости движения поездов Схема укладки переводов ПутиУсловия нормальные стесненные нормальныеПучкообразная стрелочная улица32,06 32,066,4 – 6,5 78,40 46,81 46,8132,06 – – 25,82 25,827,5 и более 78,40 46,81 46,8125,82 25,82 25,82 25,82 25,82
|
6. Стрелочные улицы. 6. Стрелочные улицы Схемы взаимной укладки стрелочных переводов
6. Стрелочные улицы 6.1. Схемы взаимной укладки стрелочных переводов
Для обеспечения безопасности движения поездов на станции и недопущения нахождения подвижного состава на двух кривых одновременно при сооружении пути предусматриваются прямые вставки между двумя смежными стрелочными переводами (рис. 6.1).
-
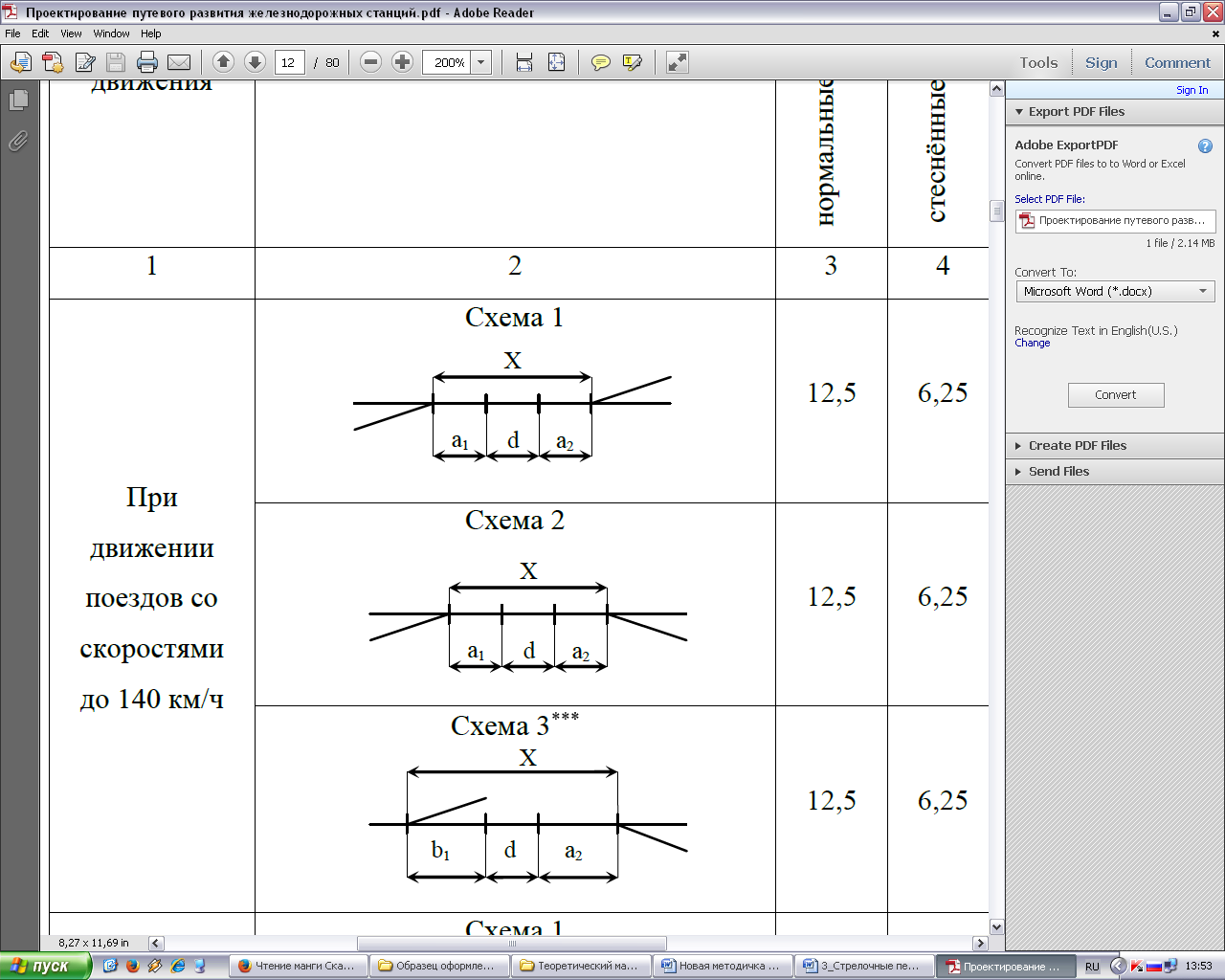
Схема 1
|
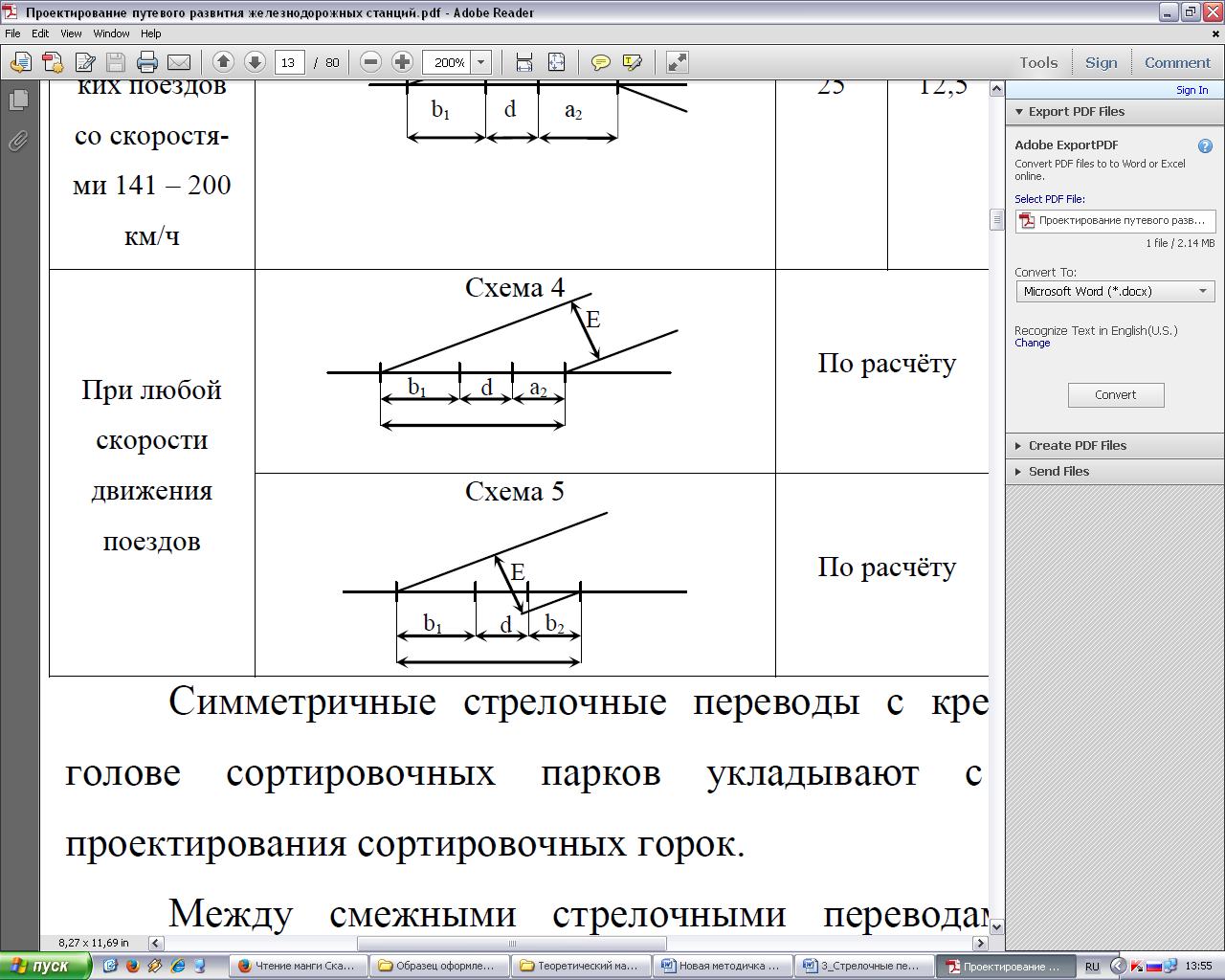
Схема 4
|
Схема 2

|
Схема 5

|
Схема 3

|
|
Рис. 6.1. Схемы взаимной укладки стрелочных переводов
Прямую вставку d между смежными стрелочными переводами укладывают (табл. 6.1):
при встречной укладке переводов с путями, направленными в разные строны (схема 1) или в одну сторону от основного пути (схема 2) – между стыками рамных рельсов стрелочных переводов;
при попутной укладке переводов (схема 3) – между трцом крестовины первого перевода и началом рамного рельса второго перевода;
при ответвлении боковых путей в одну сторону (схема 4) – между торцом крестовины первого перевода и началом рамного рельса второго;
при ответвлении двух параллельных путей в разные стороны (схема 5) – между торцами крестовин переводов.
Величина прямой вставки d при смежной укладке стрелочных переводов зависит от назначения путей, на которых переводы укладывают, типа схемы, а также от допускаемых скоростей движения по стрелочным переводам.
Для схем 4 и 5 величину прямой вставки d определяют по следующим формулам:
-
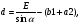
|
(6.1)
|
Е – ширина междупутья, м;
α – угол крестовины, ˚;
b1 – расстояние от центра первого перевода до торца его крестовины, м;
a2 – расстояние от начала рамных рельсов до центра второго перевода, м.
-
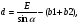
|
(6.2)
|
Между стрелочным переводом и началом кривой также укладывается прямая вставка, которая обозначается буквой f и рассчитывается по формуле:
-
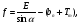
|
(6.3)
|
bn – расстояние от центра перевода до торца его крестовины, м;
Tm – тангенс кривой, м.
Тангенс кривой – это расстояние от вершины угла поворота до начала и конца кривой (измеряется в метрах). Не путать с тригонометрическим тангенсом, который является относительной и безразмерной величиной.
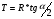 , ,
|
(6.4)
|
R – радиус закрестовинной кривой, м;
α – угол крестовины, ˚.
Таблица 6.1
Минимальные величины вставок d, м при укладке стрелочных переводов на новых и переустраиваемых станциях
Скорости движения поездов
|
Схема укладки переводов
|
Пути
|
главные
|
приемоотправочные
|
прочие
|
Условия
|
нормальные
|
стесненные
|
нормальные
|
стесненные
|
нормальные
|
стесненные
|
До 120 км/ч
|
1
|
12,5
|
6,25
|
12,5
|
6,25
|
0*
|
0*
|
2
|
12,5
|
6,25
|
6,25
|
6,25**
|
0*
|
0
|
3***
|
12,5
|
6,25
|
6,25
|
4,5
|
4,5
|
4,5
|
124 – 160 км/ч
|
1
|
25
|
12,5
|
Те же, что и при движении поездов со скоростями до 120 км/ч
|
2
|
3
|
При любой скорости
|
4
|
По расчету
|
По расчету но не менее
|
5
|
12,5
|
12,5
|
12,5
|
4,5
|
* - с разрешения инстанции, утверждающей проектом железнодорожных станций, или инстанций, согласовывающей проекты внешних железнодорожных подъездных путей, прямые вставки можно не предусматривать.
** - в стесненных условиях на приемо-отправочных путях частично переустраиваемых крупных станций укладку прямой вставки можно не предусматривать, если расстояние между остриями остряков смежных однотипных стрелочных переводов и более 8,65 м.
*** - если второй стрелочный перевод имеет марку крестовины 1/18 или 1/22, то прямая вставка d в нормальных условиях должна быть равна 25 м, а в стесненных условиях – не менее 12,5.
|
6.2. Типы стрелочных улиц
Стрелочной улицей называется путь, на котором последовательно уложены стрелочные переводы для примыкания группы параллельных путей. Они позволяют принимать поезда с перегона на любой станционный парковый путь, отправлять поезда со станции с любого паркового пути, переставлять подвижной состав с одного пути на другой.
Конструкция стрелочных улиц характеризуется взаимным расположением стрелочных переводов на соединяемых путях и определяет условия работы станции, влияет на их длину, строительные затраты и безопасность движения и маневровой работы.
Стрелочная улица должна быть спроектирована так, чтобы по возможности иметь минимальную длину. Чтобы обеспечить минимальную длину, нужно:
соблюдать по возможности минимально допустимое расстояние между стрелочными переводами,
грамотно использовать различные конструкции стрелочных улиц в различных условиях.
Различают следующие типы стрелочных улиц:
под углом крестовины (рис. 6.1);
по основному пути (рис. 6.2);
под двойным углом крестовины (рис. 6.3);
сокращенная (рис. 6.4);
комбинированная (рис. 6.5);
веерная (рис. 6.6);
пучкообразная (рис. 6.7).
Достоинства и недостатки различных типов стрелочных улиц зависят от назначения и числа присоединяемых путей, места их расположения на станции, местных условий и др.
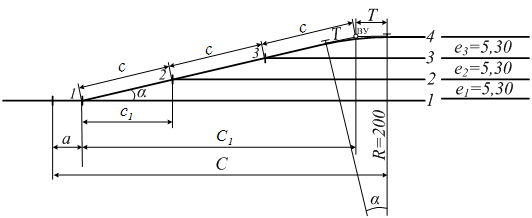
Рис. 6.1. Стрелочная улица под углом крестовины
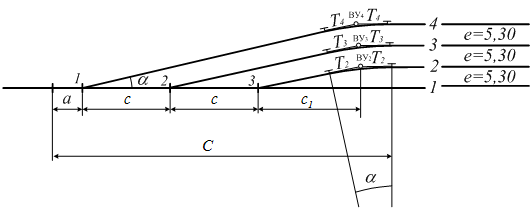
Рис. 6.2. Стрелочная улица по основному пути
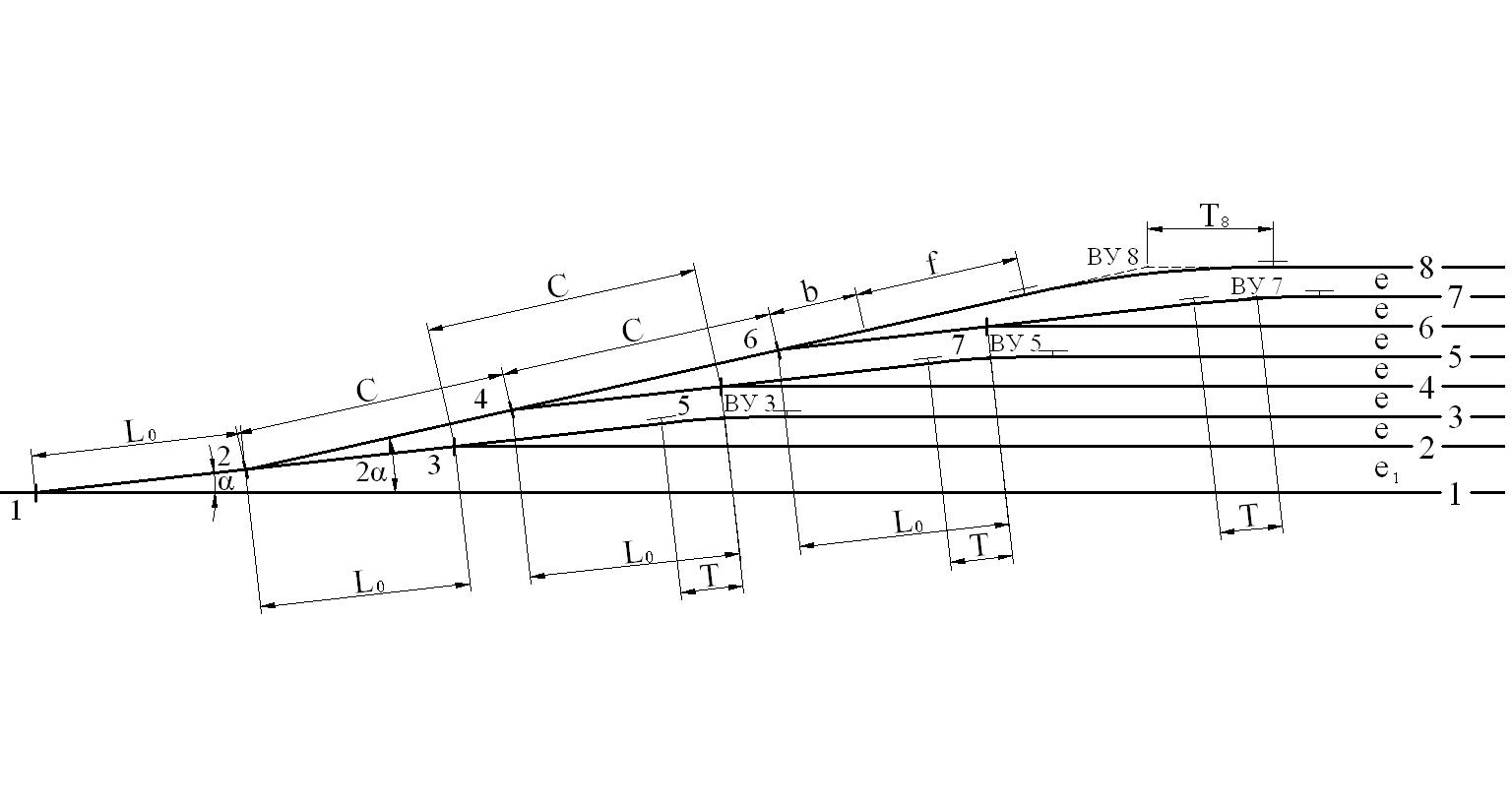
Рис. 6.3. Стрелочная улица под двойным углом крестовины
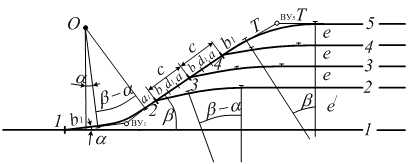
Рис. 6.4. Сокращенная стрелочная улица
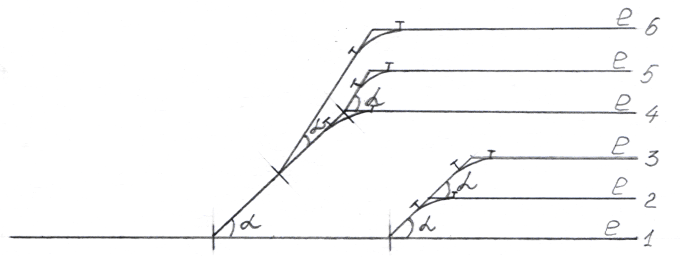
Рис. 6.5. Комбинированная стрелочная улица
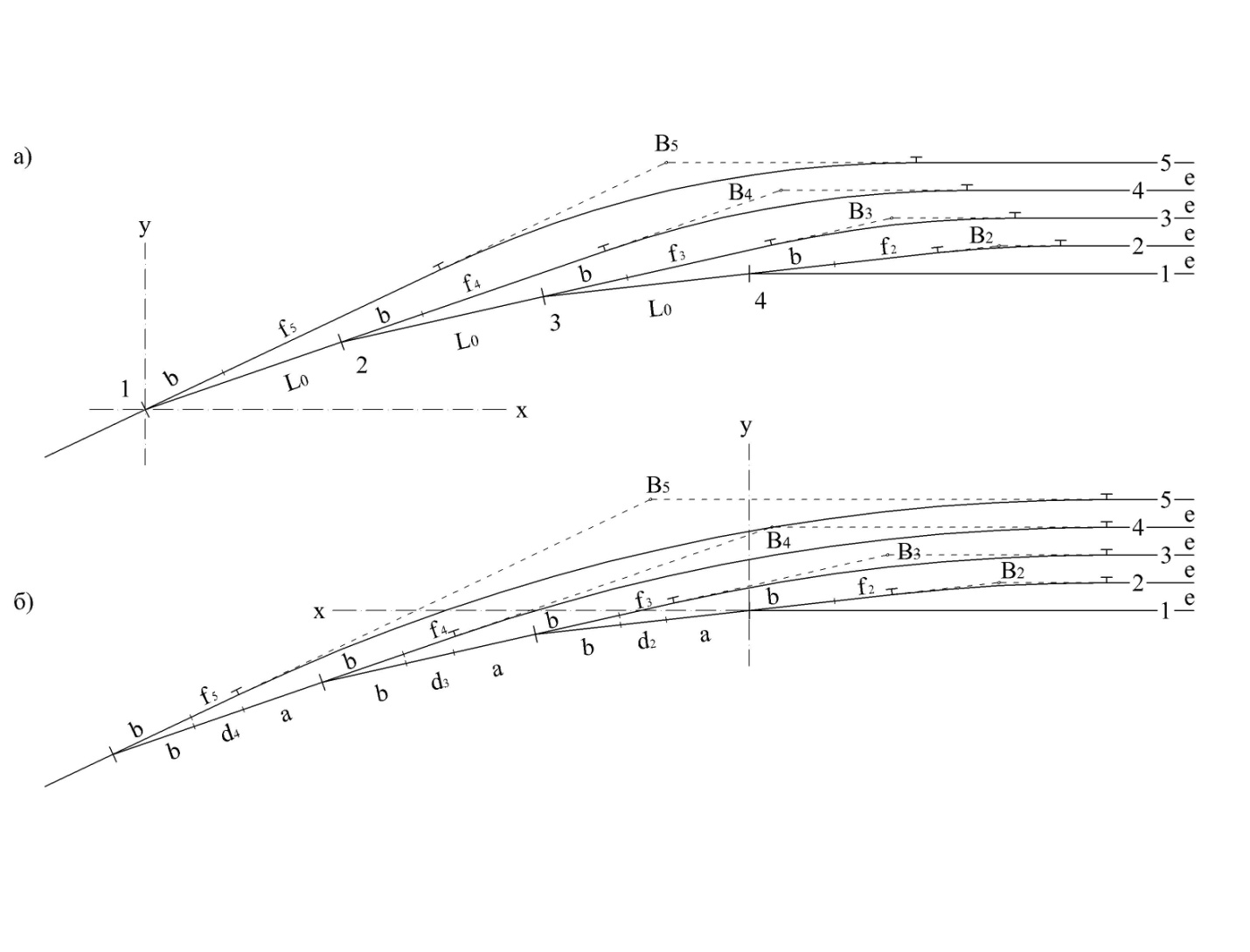 Рис. 6.6. Веерная стрелочная улица Рис. 6.6. Веерная стрелочная улица
а – неконцентрическая, б – концентрическая

Рис. 6.7. Пучкообразная стрелочная улица
Достоинством простых улиц является хорошая видимость и удобство обслуживания; недостаток – значительное увеличение длины горловины при большом количестве путей (пропорционально числу путей). Поэтому простые стрелочные улицы применяются с переводами марки 1/9 преимущественно в небольших парках (до 4-5 путей). Из двух видов простых стрелочных улиц предпочтительней первый, который имеет прямые пути в пределах полезной длины, что обеспечивает лучшую видимость при маневрах. Если основной путь стрелочной улицы является в то же время главным, надо применять стрелочную улицу под углом крестовины, чтобы на главном пути укладывать меньше стрелочных переводов.
Основное преимущество сокращенной стрелочной улицы – ее небольшая длина по сравнению с простейшими стрелочными улицами, поэтому она нашла применение в парках при ограничении длины станционной площадки. Однако при использовании сокращенных стрелочных улиц возникает необходимость уширения первого междупутья и укладки обратных кривых, что затрудняет маневровую работу на станции.
Достоинством стрелочной улицы под двойным углом крестовины является сокращение длины стрелочной зоны, а следовательно, и маневрового рейса. Данный тип стрелочной улицы применяется преимущественно в горловинах приемо-отправочных парков, имеющих более 4-5 путей.
Положительной особенностью веерных стрелочных улиц является возможность устройства выхода на основной путь, расположенный к парку под углом более 2 углов α, а также для крайних пучков больших парков.
Веерные улицы могут быть концентрическими и неконцентрическими. В концентрических улицах центр всех кривых находится в одной точке в независимости от величины радиуса. В неконцентрических улицах центры кривых не совпадают.
Пучкообразная стрелочная улица обладает самой короткой длиной при наименьшем числе углов поворота при движении на пути парка с основного пути. Этот тип стрелочных улиц применяется в горочных горловинах сортировочных парков, где продолжительность занятия элементов горловины должна быть минимальной.
Комбинированные улицы представляют собой различные комбинации простых улиц с увеличением угла наклона к основному пути. Они возникают при большом числе путей в парках, что затрудняет использование какого-либо одного конкретного типа стрелочных улиц.
Прежде чем уложить стрелочную улицу на местность ее рассчитывают. Расчет стрелочной улицы заключается в определении координат характерных ее точек и размеров элементов:
вершин углов поворота;
центров стрелочных переводов;
тангенсов (Т) кривых;
длин прямых вставок (f и d).
Предельный столбик – путевой сигнальный знак. Предельные столбики устанавливаются посередине междупутья в том месте, где расстояние между осями сходящихся путей составляет 4100 мм. На существующих станционных путях, по которым не обращается подвижной состав, построенный по габариту Т, разрешается сохранить расстояние 3810 мм. На перегрузочных путях с суженным междупутьем предельные столбики устанавливаются в том месте, где ширина междупутья достигает 3600 мм. На кривых участках пути эти расстояния увеличиваются в соответствии с нормами, установленными Инструкцией по применению габаритов приближения строений.
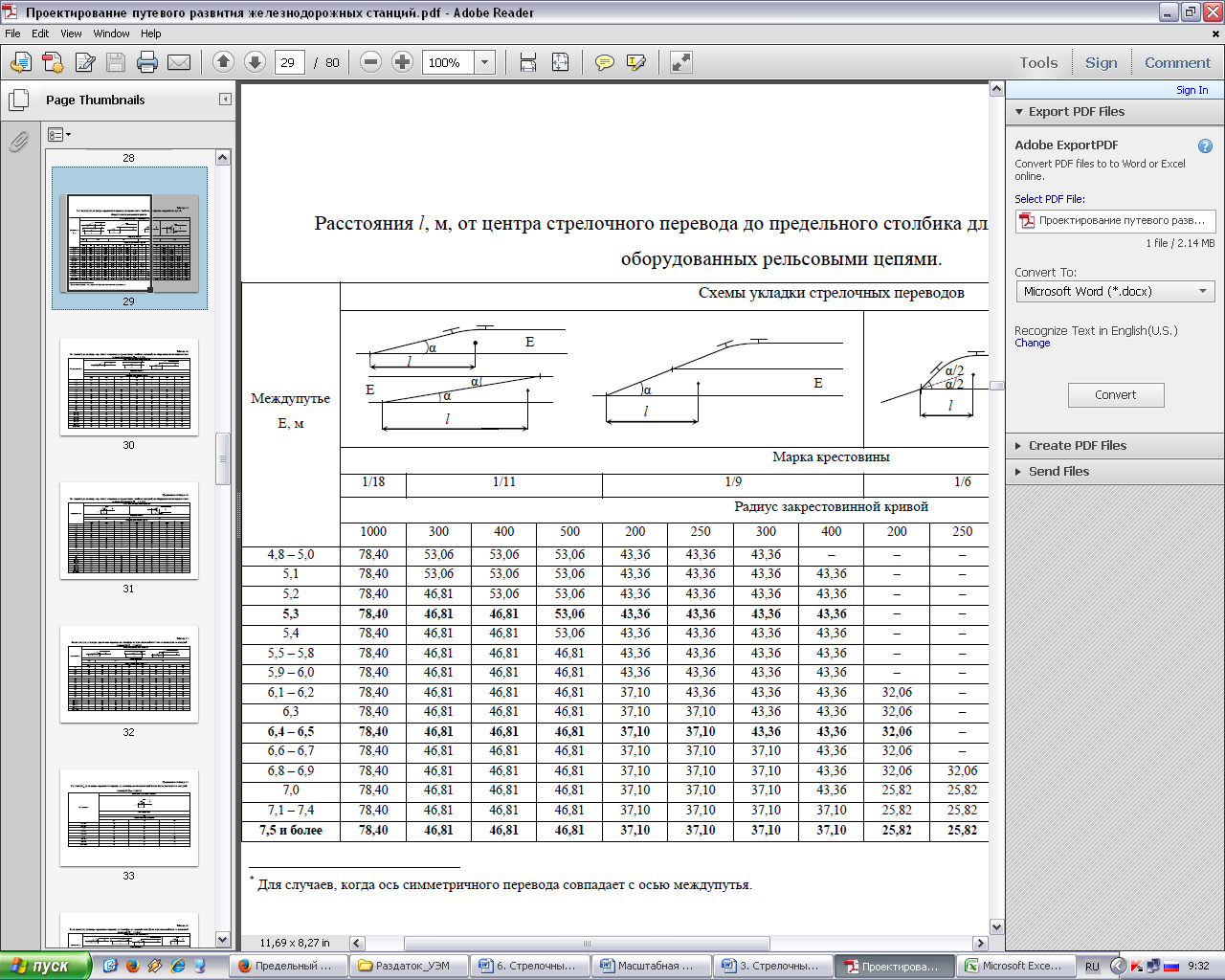
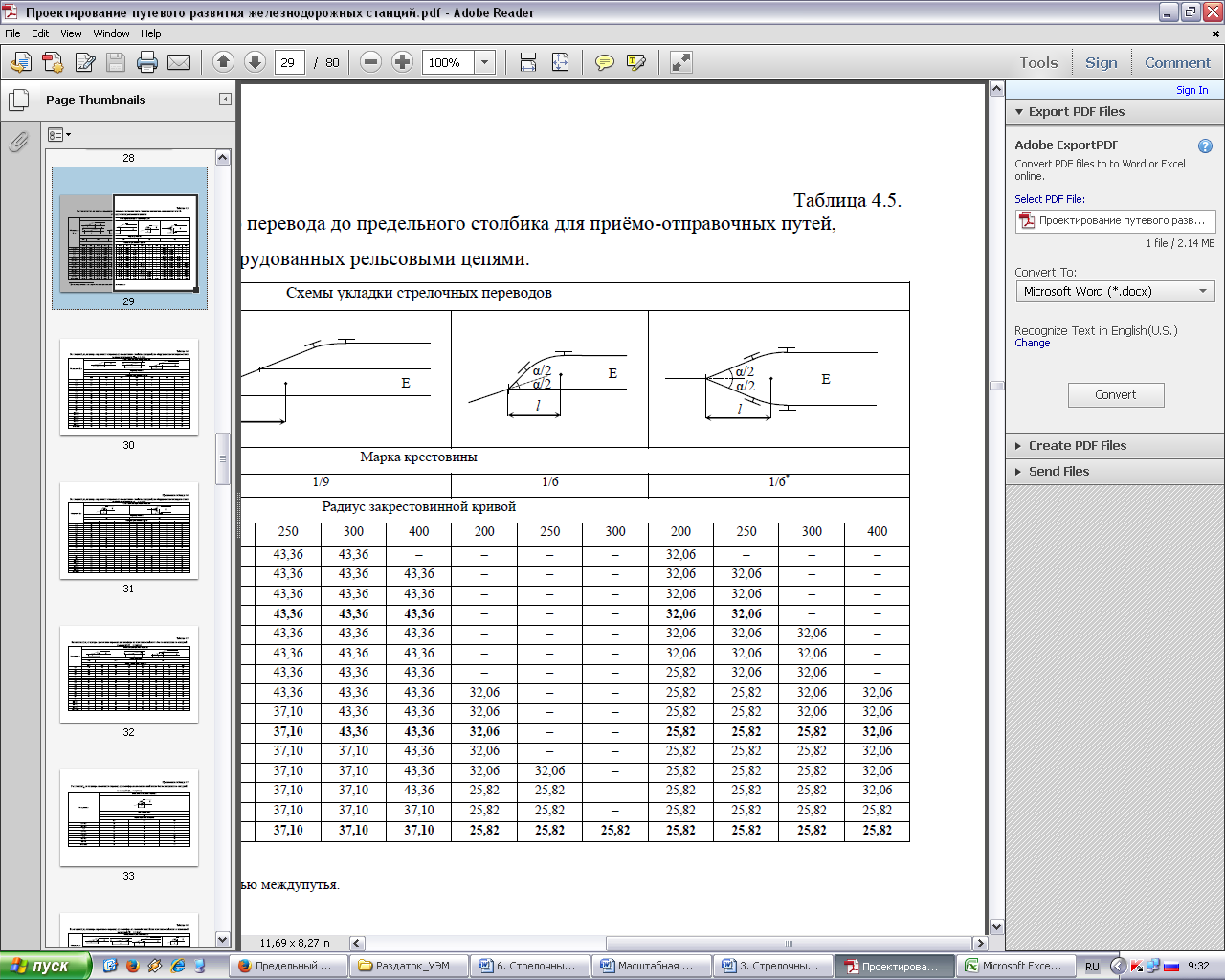
Расстояние от центра стрелочного перевода до предельного столбика на путях, не оборудованных рельсовыми цепями, определяется расчетным способом. Расстояния до предельных столбиков на участках, оборудованных рельсовыми цепями, приведены в табл. 6.2.
Таблица 6.2
Расстояние от центра стрелочного перевода до предельных столбиков на приемо-отправочных путях, оборудованных рельсовыми цепями
Ширина междупутья, м
|
Схема укладки стрелочных переводов
|
|
|

|
Марка крестовины
|
|
1/18
|
1/11
|
1/9
|
1/6
|
1/6*
|
Радиус кривой, м
|
|
1000
|
300
|
400
|
500
|
200
|
250
|
300
|
400
|
200
|
250
|
300
|
200
|
250
|
300
|
400
|
4,8 – 5,0
|
78,40
|
53,06
|
53,06
|
53,06
|
43,36
|
43,36
|
43,36
|
–
|
–
|
–
|
–
|
25,82__25,82'>32,06__32,06'>32,06
|
–
|
–
|
–
|
5,1
|
78,40
|
53,06
|
53,06
|
53,06
|
43,36
|
43,36
|
43,36
|
43,36
|
–
|
–
|
–
|
32,06
|
32,06
|
–
|
–
|
5,2
|
78,40
|
46,81
|
53,06
|
53,06
|
43,36
|
43,36
|
43,36
|
43,36
|
–
|
–
|
–
|
32,06
|
32,06
|
–
|
–
|
5,3
|
78,40
|
46,81
|
46,81
|
53,06
|
43,36
|
43,36
|
43,36
|
43,36
|
–
|
–
|
–
|
32,06
|
32,06
|
–
|
–
|
5,4
|
78,40
|
46,81
|
46,81
|
53,06
|
43,36
|
43,36
|
43,36
|
43,36
|
–
|
–
|
–
|
32,06
|
32,06
|
32,06
|
–
|
5,5 – 5,8
|
78,40
|
46,81
|
46,81
|
46,81
|
43,36
|
43,36
|
43,36
|
43,36
|
–
|
–
|
–
|
32,06
|
32,06
|
32,06
|
–
|
5,9 – 6,0
|
78,40
|
46,81
|
46,81
|
46,81
|
43,36
|
43,36
|
43,36
|
43,36
|
–
|
–
|
–
|
25,82
|
32,06
|
32,06
|
–
|
6,1 – 6,2
|
78,40
|
46,81
|
46,81
|
46,81
|
37,10
|
43,36
|
43,36
|
43,36
|
32,06
|
–
|
–
|
25,82
|
25,82
|
32,06
|
32,06
|
6,3
|
78,40
|
46,81
|
46,81
|
46,81
|
37,10
|
37,10
|
43,36
|
43,36
|
32,06
|
–
|
–
|
25,82
|
25,82
|
32,06
|
32,06
|
6,4 – 6,5
|
78,40
|
46,81
|
46,81
|
46,81
|
37,10
|
37,10
|
43,36
|
43,36
|
32,06
|
–
|
–
|
25,82
|
25,82
|
25,82
|
32,06
|
6,6 – 6,7
|
78,40
|
46,81
|
46,81
|
46,81
|
37,10
|
37,10
|
37,10
|
43,36
|
32,06
|
–
|
–
|
25,82
|
25,82
|
25,82
|
32,06
|
6,8 – 6,9
|
78,40
|
46,81
|
46,81
|
46,81
|
37,10
|
37,10
|
37,10
|
43,36
|
32,06
|
32,06
|
–
|
25,82
|
25,82
|
25,82
|
32,06
|
7,0
|
78,40
|
46,81
|
46,81
|
46,81
|
37,10
|
37,10
|
37,10
|
43,36
|
25,82
|
25,82
|
–
|
25,82
|
25,82
|
25,82
|
32,06
|
7,1 – 7,4
|
78,40
|
46,81
|
46,81
|
46,81
|
37,10
|
37,10
|
37,10
|
37,10
|
25,82
|
25,82
|
–
|
25,82
|
25,82
|
25,82
|
25,82
|
7,5 и более
|
78,40
|
46,81
|
46,81
|
46,81
|
37,10
|
37,10
|
37,10
|
37,10
|
25,82
|
25,82
|
25,82
|
25,82
|
25,82
|
25,82
|
25,82
|
* Для случаев, когда ось симметричного перевода совпадает с осью междупутья
6.3. Порядок выполнения работы
Задание. Рассчитать и начертить стрелочную улицу. Пронумеровать пути и центры стрелочных переводов, отметить вершины углов, тангенсы кривых и предельные столбики. Рассчитать: длины прямых вставок, тангенсов, расстояния между центрами переводов; координаты вершин углов, центров переводов и предельных столбиков.
Чертеж выполняется на листе А3 (или двух листах А4, склеенных в длину) в масштабе М 1:1000. Название чертежа: Стрелочная улица … (вместо многоточия указывается заданный тип стрелочной улицы).
На черновике схематично изобразить стрелочную улицу (не в масштабе).
Пронумеровать пути арабскими цифрами (начиная снизу).
Пронумеровать центры стрелочных переводов (далее ЦП) арабскими цифрами, двигаясь слева направо.
Отметить и пронумеровать вершины углов кривых (ВУ1, ВУ2 и т.д.). Номер вершины угла соответствует номеру пути.
Отметить и пронумеровать тангенсы кривых (Т1, Т2 и т.д.). Тангенсы отмечаются с обеих сторон от вершины угла. Номер тангенса соответствует номеру пути, на котором располагается кривая.
Отметить и пронумеровать прямые вставки между стрелочными переводами (d) и прямые вставки между стрелочными переводами и кривыми (f), а также элементы стрелочных переводов (a и b).
По формулам, приведенным в теоретической части, рассчитать длины прямых вставок и тангенсов кривых. Для марки крестовины 1/9 радиус закрестовинной кривой принимается равным 200 м, для 1/11 – 300 м, для 1/18 – 1000 м.
Рассчитать расстояния между центрами переводов.
Рассчитать координаты всех объектов: центров стрелочных переводов, вершин углов кривых, предельных столбиков. Ось абсцисс (X) совпадает с осью первого пути. Ось ординат (Y) проходит вертикально через ЦП1. Расчет производится с использованием простейших тригонометрических функций: sin, cos, tg.
Предельные столбики устанавливаются там, где ширина междупутья составляет 4,1 м (если столбик не расположен между прямым и кривым путем). Соответственно, расстояние от ПС до оси каждого из путей равно половине ширины междупутья. Если ПС расположен между прямым и кривым путем, то расстояние от столбика до кривого пути будет больше, чем до прямого. Это связано с необходимостью уширения горизонтальных размеров габарита приближения строений на кривом участке пути. Номер предельного столбика соответствует номеру центра перевода, к которому он относится (например, ПС1, ПС2 и т.д.).
Начертить стрелочную улицу в масштабе, отметить и пронумеровать все элементы.
В четырех таблицах указать исходные данные, условные обозначения и все расчетные величины. В первую таблицу заносятся исходные данные по варианту; во вторую – координаты объектов (ЦП, ПС, ВУ); в третью – длины прямых вставок (d и f), размеры элементов стрелочных переводов (a и b), длины тангенсов кривых, расстояния между соседними стрелочными переводами; в четвертую – условные обозначения (Т, ЦП, ПС, ВУ, R).
Все расчеты выполняются на отдельном листе и прикладываются к чертежу.
6.4. Контрольные вопросы
Классификация стрелочных улиц.
Что такое тангенс кривой, и как он рассчитывается?
Что такое предельный столбик? Правила установки предельных столбиков.
Как рассчитываются длины прямых вставок?
Как рассчитываются координаты объекта? Конкретный объект называет преподаватель.
Приложение
Таблица П 6.1 - Тригонометрические функции углов, кратных углам крестовины
Марка крестовины
|
Число углов поворота
|
Угол поворота
|
sin α
|
cos α
|
tg α
|
ctg α
|
sec α
|
cosec α
|
1/18
|
0,5
|
1º35′06,25″
|
0,027661
|
0,999617
|
0,027672
|
36,137975
|
1,000383
|
36,151775
|
1
|
3º10′12,5″
|
0,055301
|
0,998470
|
0,055386
|
18,05515
|
1,001533
|
18,082825
|
1/11
|
0,5
|
2º35′50″
|
0,045315
|
0,998973
|
0,045361
|
22,04529
|
1,001028
|
22,06796
|
1
|
5º11′40″
|
0,090536
|
0,995893
|
0,090909
|
10,99997
|
1,004124
|
11,04533
|
1,5
|
7º47′30″
|
0,135571
|
0,990768
|
0,136835
|
7,30808
|
1,009318
|
7,376183
|
2
|
10º23′20″
|
0,180328
|
0,983606
|
0,183334
|
5,45453
|
1,016667
|
5,54544
|
3
|
15º35′00″
|
0,268640
|
0,963241
|
0,278891
|
3,585624
|
1,038162
|
3,722459
|
1/9
|
0,5
|
3º10′12,5″
|
0,055301
|
0,998470
|
0,055386
|
18,05515
|
1,001533
|
18,082825
|
1
|
6º20′25″
|
0,110433
|
0,993884
|
0,111113
|
8,999875
|
1,006154
|
9,055265
|
1,5
|
9º30′37,5″
|
0,165227
|
0,986256
|
0,167529
|
5,969098
|
1,013940
|
6,052282
|
2
|
12º40′50″
|
0,219515
|
0,975609
|
0,225003
|
4,444382
|
1,025001
|
4,555495
|
2,5
|
15º51′02,5″
|
0,273132
|
0,961977
|
0,283927
|
3,522027
|
1,039526
|
3,661240
|
3
|
19º01′15″
|
0,325912
|
0945400
|
0,344734
|
2,900784
|
1,057753
|
3,068315
|
4
|
25º21′40″
|
0,428322
|
0,903626
|
0,474003
|
2,109689
|
1,106652
|
2,334693
|
5
|
31º42′05″
|
0,525492
|
0,850798
|
0,617646
|
1,618260
|
1,75366
|
1,902977
|
6
|
38º02′30″
|
0,616234
|
0,787563
|
0,782457
|
1,278025
|
1,269740
|
1,622759
| |
|
|
 Скачать 1.04 Mb.
Скачать 1.04 Mb.




 Рис. 6.6. Веерная стрелочная улица
Рис. 6.6. Веерная стрелочная улица



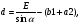
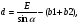
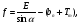
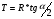 ,
,
