8_ Дисперсионный анализ-1. 8. Дисперсионный анализ. 1 Понятие, назначение дисперсионного анализа. Виды дисперсионного анализа
 Скачать 0.57 Mb.
|
|
8.3 Пример использования однофакторного дисперсионного анализа Пример 1. Поставки продукции осуществляются тремя поставщиками («Мега+», «Коста» и «Трамп») в разное время: дневные часы, ночные смены и в пересменку. Контроль за качеством продукции в дневное время выше, чем в другое время. Собраны данные с оценками качества продукции (в баллах). Необходимо выяснить, есть ли отличие в качестве продукции, которая поставляется в разное время. Таблица 8.5 Таблица исходных данных
Таблица 8.6 Данные, подготовленные для анализа
Таблица 6.7 Однофакторный дисперсионный анализ
Результаты расчета показывают, что  , следовательно, существенное отличие в качестве поставляемой продукции в разное время отсутствует. Кроме того, достигнутое значение уровня значимости P-значение превышает 0,05, т.е. нулевая гипотеза на указанном уровне значимости не отвергается. Можно считать доказанным тот факт, что качество поставляемой продукции не зависит от времени поставки и является одинаковым в разное время.Пример 2. Требуется оценить влияние уровня рекламы внутри магазина на объемы продаж. Имеются следующие данные по 30 торговым точкам: Таблица 8.8 Таблица исходных данных
Таблица 8.9 Данные подготовленные для анализа
Таблица 8.10 Однофакторный дисперсионный анализ
Результаты анализа показывают, что разница в объемах продаж в магазинах с разным уровнем рекламы, является значимой (существенной). Об этом свидетельствует значение F: 17,943 > 3,354, а также малое значение достигнутого уровня значимости (р – значение = 1,10 Е-0,05). Следовательно, нулевая гипотеза отклоняется и принимается альтернативная о том, что уровень рекламы влияет на объемы продаж, причем наблюдается прямая зависимость, т.е. более высокому уровню рекламы соответствуют более высокие объемы продаж. 8.4 Априорные контрасты и апостериорные критерии При проведении дисперсионного анализа в дополнение к выявлению наличия различий между средними значениями можно узнать, какие именно групповые средние значения различаются. Есть два типа критериев для сравнения средних значений: априорные контрасты и апостериорные критерии. Контрасты – это критерии, которые применяются до проведения эксперимента, апостериорные критерии применяются после проведения эксперимента. Кроме того можно также осуществлять проверку наличия трендов по уровням (категориям). Контраст представляет собой взвешенную сумму (линейную комбинацию) групповых средних значений зависимой переменной для каждого уровня независимой переменной. В зависимости от того, как заданы коэффициенты, контрасты позволяют проверять гипотезы о различии средних значений отдельных уровней или комбинаций уровней анализируемого фактора (или факторов). Обычно весовые коэффициенты контраста должны в сумме давать 0. Для этого должны выполняться следующие обязательные условия:
Таким образом, если изучаемый фактор имеет три уровня – А, В и С, и необходимо "выявить контраст" между средними значениями уровней А и С (т.е. сравнить эти значения статистически), коэффициентам контраста можно придать следующие значения: -1; 0; 1 (или -0.5; 0; 0.5 – выбор значений весовых коэффициентов в контрастах совершенно произволен - главное, чтобы в сумме они давали 0). Аналогично, при сравнении средних значений уровней А и В коэффициенты соответствующего контраста составят: -1; 0; 1. При необходимости можно сравнивать также комбинации из нескольких уровней фактора с другими его уровнями (или комбинациями уровней), что открывает широкие возможности для проверки самых разнообразных гипотез в отношении анализируемых данных. Если сравнивать среднее значение уровня А с общим средним значением уровней В и С, то можно выбрать коэффициенты контраста: 2; -1; -1. Пример. Пончики впитывают различное количество жира в процессе их приготовления. В эксперименте используются три типа жиров: арахисовое масло, кукурузное масло и свиное сало. Арахисовое и кукурузное масло являются ненасыщенными жирами, а топленое сало - насыщенным жиром. Выясняя, зависит ли количество расходуемого жира от типа используемого жира, можно выбрать априорный контраст, позволяющий выяснить, различаются ли количества впитывающегося жира для насыщенных и ненасыщенных жиров. В этом случае коэффициенты могут принять следующие значения: -1; -1; 2. Апостериорные критерии применяются в случае подтверждения различий средних значений. Установив, что различия средних значений существуют, с помощью апостериорных критериев диапазона и парных множественных сравнений можно выяснить, какие именно средние различаются. Критерии диапазона выявляют однородные подмножества средних, не различающихся между собой. Парные множественные сравнения проверяют различия между каждой парой средних значений, на основании чего формируется матрица различий на заданном уровне значимости. 8.5 Однофакторный дисперсионный анализ для связанных выборок (ANOVA с повторными измерениями) Метод применяется в тех случаях, когда исследуется влияние разных значений фактора (градаций фактора) на одну и ту же выборку. (Например, одни и те же респонденты в разных условиях.). Условий (градаций) должно быть не менее трех. В этом случае различия отдельных значений могут быть вызваны не только влиянием фактора, но и индивидуальными различиями между элементами выборки (респондентами). При анализе несвязанных выборок это обстоятельство не оказывало воздействия за счет того, что выборки были различны, а это приводило к случайным причинам различий, - здесь же индивидуальные различия между элементами выборки (респондентами) необходимо особо учитывать. Индивидуальные различия могут оказаться более значимыми, чем результаты воздействия фактора. Проверяемые гипотезы: H0(A): Различия независимой величины при разных градациях фактора являются не более выраженными, чем различия, обусловленные случайными причинами. H1(A): Различия независимой величины при разных градациях фактора являются более выраженными, чем различия, обусловленные случайными причинами. Hο(Б): Индивидуальные различия между элементами выборки являются не более выраженными, чем различия, обусловленные случайными причинами. H1(Б): Индивидуальные различия между элементами выборки являются более выраженными, чем различия, обусловленные случайными причинами. Результаты вычислений могут быть представлены в следующем виде (табл.8.11). Таблица 8.11 Результаты анализа
Использованы следующие обозначения и расчетные формулы: 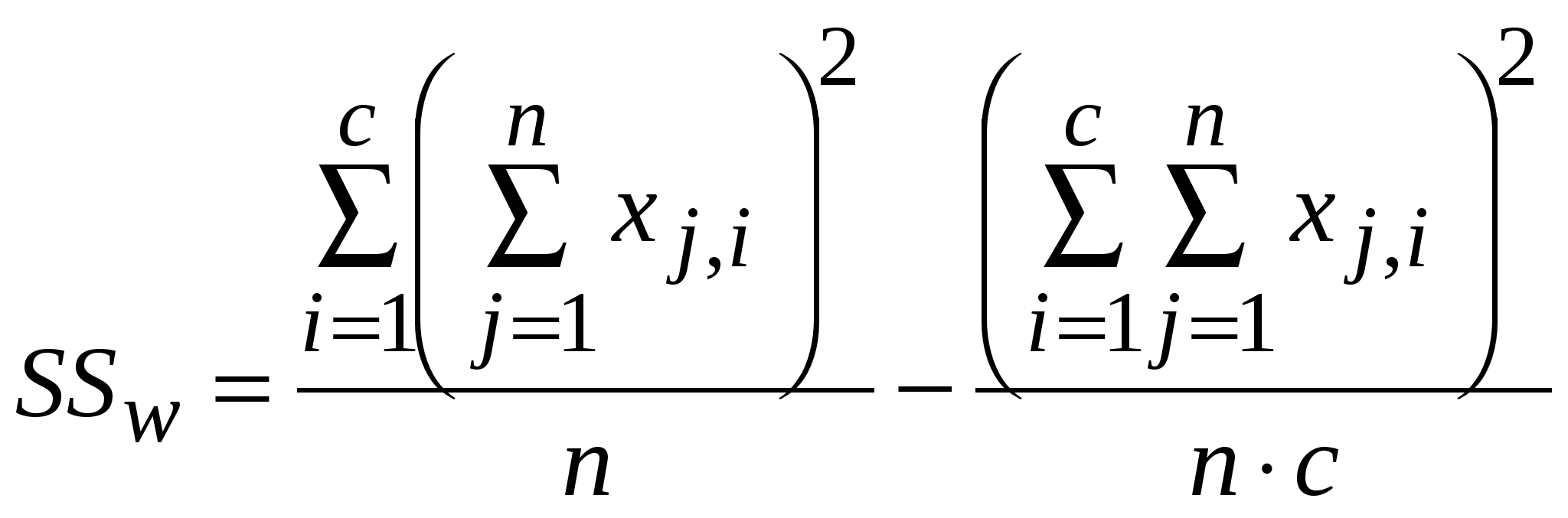 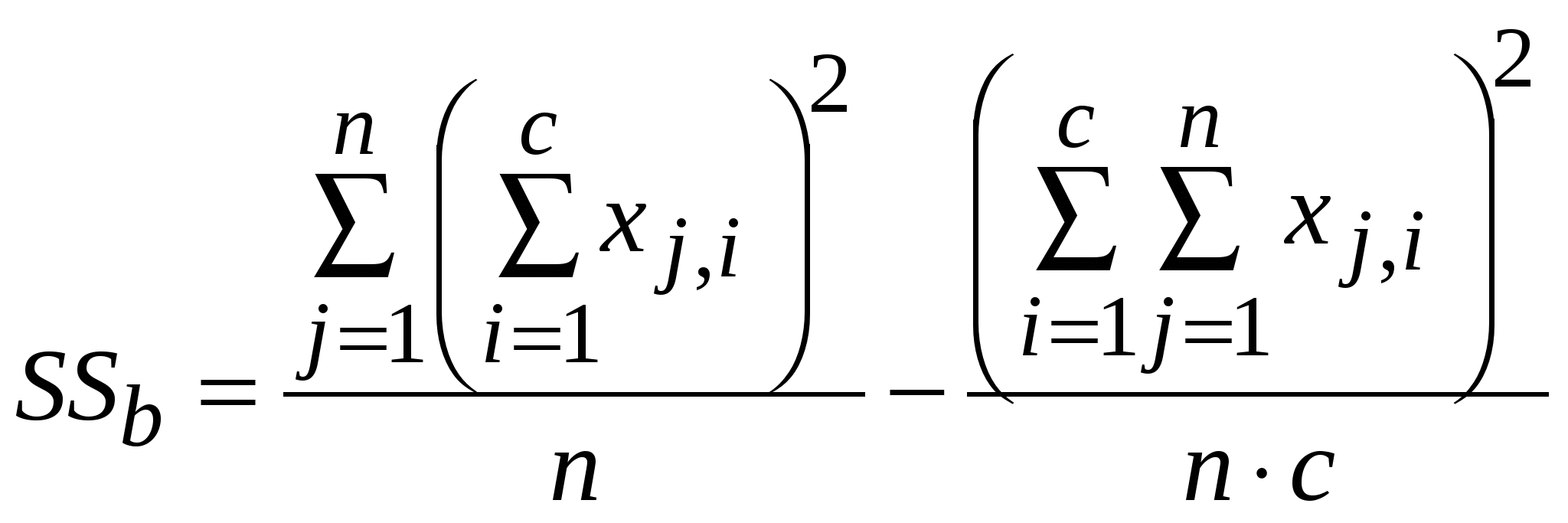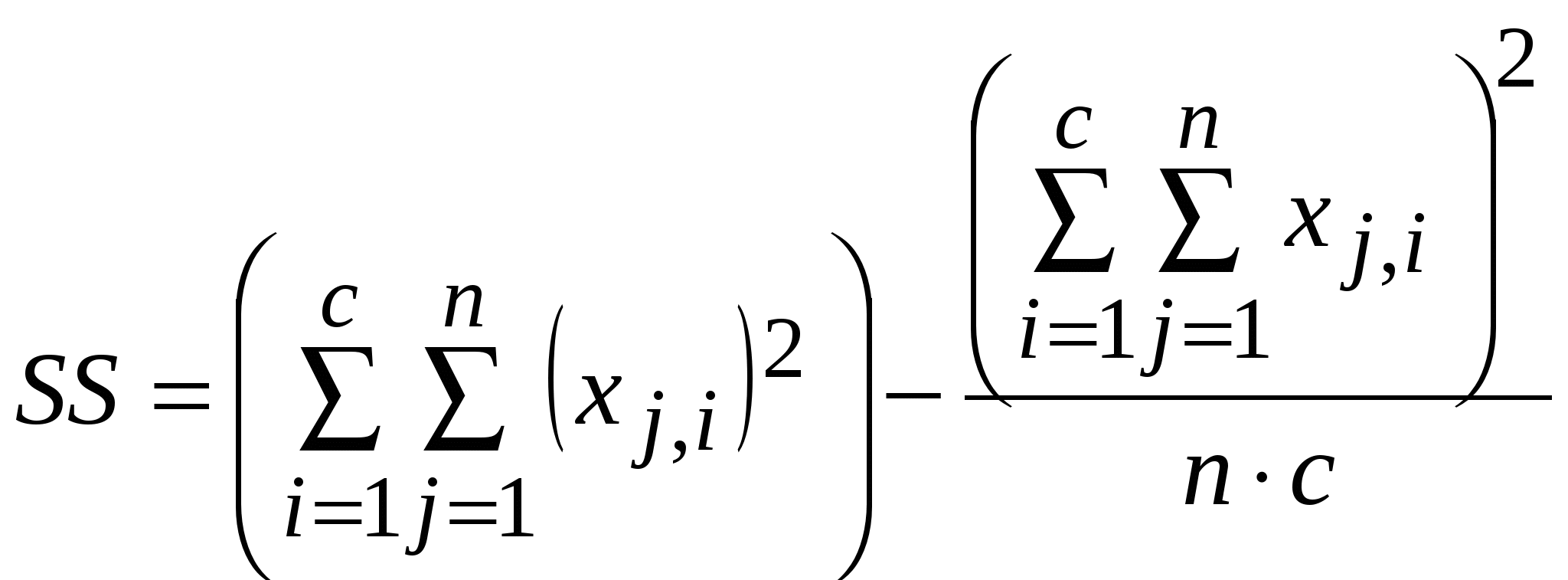– объем выборки; – количество значений для каждого элемента выборки; – общее количество измерений; ; ; ; – сумма квадратов для ошибки.Статистическая проверка гипотезы о наличии различий осуществляется на основании  – статистики:  ,  ; ,  ;Если  , то нулевая гипотеза А отвергается, различия при разных значениях фактора являются более выраженными, чем различия, обусловленные случайными причинами.Если  , то нулевая гипотеза Б отвергается, различия при разных значениях фактора являются более выраженными, чем различия, обусловленные случайными причинами.Ограничения метода дисперсионного анализа для связанных выборок: 1. Дисперсионный анализ для связанных выборок требует не менее трех градаций фактора и не менее двух элементов выборки в каждой группе. 2. Должно соблюдаться правило равенства дисперсий в каждой группе. Это условие косвенно выполняется за счет одинакового количества наблюдений в каждой группе. 3. Результативный признак должен быть нормально распределен в исследуемой выборке. Непараметрический вариант этого вида анализа – критерий Фридмана – применяется в тех случаях, когда результативный признак является порядковой величиной или если не выполняются перечисленные требования. | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
