8_ Дисперсионный анализ-1. 8. Дисперсионный анализ. 1 Понятие, назначение дисперсионного анализа. Виды дисперсионного анализа
 Скачать 0.57 Mb.
|
|
8.5 Способы реализации однофакторного дисперсионного анализа с повторными измерениями Данный вид дисперсионного анализа используется, когда разным градациям фактора соответствует одна и та же выборка (зависимые выборки). С другой стороны, эти выборки можно рассматривать как независимые и применить обычный вариант ANOVA, но ANOVA с повторными измерениями имеет преимущество – он позволяет исключить из общей дисперсии данных ту ее часть, которая обусловлена индивидуальными различиями в уровне зависимой переменной, т.е. из остаточной внутригрупповой изменчивости вычитается компонент, обусловленный индивидуальными различиями. Это позволяет данному варианту дисперсионного анализа быть более чувствительным к влиянию изучаемых факторов, за счет уменьшения дисперсии ошибки факторной модели. Существует два типа моделей ANOVA с повторными измерениями: 1) Одномерная модель основана на предположении, что каждому уровню внутригруппового фактора соответствует повторное измерение одной и той же зависимой переменной (следовательно, эти изменения положительно коррелируют). Данный одномерный подход основан на применении F-отношений, но имеет определенные ограничения: дисперсии зависимой переменной для разных уровней внутригруппового фактора не различаются и корреляции между повторными измерениями есть и они положительны. Данное предположение проверяется с помощью теста сферичности ковариационно-дисперсионной матрицы Моучли. 2) Многомерная модель свободна от допущения о коррелированности измерений зависимой переменной (т.е. о сферичности). В этом случае применяется не F-критерий, а многомерные тесты, такие как «След Пиллая» (Pillai's Trace) и «λ-Вилкса» (Wilks' Lambda). 8.6 Многофакторный дисперсионный анализ Принципиальной разницы между многофакторным и однофакторным дисперсионным анализом нет. Многофакторный анализ не меняет общую логику дисперсионного анализа, а лишь несколько усложняет ее, поскольку, кроме учета влияния на зависимую переменную каждого из факторов по отдельности, следует оценивать и их совместное действие. Таким образом, то новое, что вносит в анализ данных многофакторный дисперсионный анализ, касается в основном возможности оценить межфакторное взаимодействие. Тем не менее, по-прежнему остается возможность оценивать влияние каждого фактора в отдельности. В этом смысле процедура многофакторного дисперсионного анализа (в варианте ее компьютерного использования) несомненно более экономична, поскольку всего за один запуск решает сразу две задачи: оценивается влияние каждого из факторов и их взаимодействие. Рассмотрим многофакторный анализ на примере двухфакторного. Двухфакторный дисперсионный анализ позволяет проверить эффекты влияния обоих факторов на зависимую переменную одновременно, а не по отдельности. Кроме этого, можно проверить гипотезу об эффекте взаимодействия между двумя независимыми переменными (рис.8.6).  Рис.8.6 Двухфакторный дисперсионный анализ Например, компания хочет проверить эффективность своей рекламы (табл. 8.12). Выбран продукт, и созданы два типа рекламных роликов: серьезный и смешной. Реклама размещается в рабочие и выходные дни. Выбраны 16 потенциальных зрителей, которые распределяются по группам случайным образом: Группа 1: Смешной ролик, рабочий день Группа 2: Смешной ролик, выходной день Группа 3: Серьезный ролик, рабочий день Группа 4: Серьезный ролик, выходной день Эта схема 2×2, так как каждая переменная состоит из двух уровней. После того, как каждый зритель просмотрел ролик, его просят оценить эффективность рекламы (привлекательность, ясность, краткость ролика и т.д.) по двадцатибалльной шкале. Необходимо на уровне значимости α выяснить зависимость оценок от указанных факторов, используя двухфакторный дисперсионный анализ. Таблица 8.12 Оценки эффективности рекламы
Исследуемые группы называют эффектами обработки (treatment groups): Двухфакторный дисперсионный анализ позволит проверить эффекты влияния типа ролика и типа дня одновременно, а не по отдельности, а также гипотезу об эффекте взаимодействия между двумя переменными. Наличие значимого эффекта будет означать, что тип ролика по-разному влияет на эффективность рекламы в зависимости от типа дня. Схема двухфакторного дисперсионного анализа имеет несколько нулевых гипотез: одна для каждой независимой переменной и одна для взаимодействия. Н0: Тип ролика и день не имеют эффекта взаимодействия на эффективность рекламы. Н1: Тип ролика и день имеют эффект взаимодействия на эффективность рекламы. Н0: Эффективность рекламы не зависит от типа ролика. Н1: Эффективность рекламы зависит от типа ролика. Н0: Эффективность рекламы не зависит от типа дня. Н1: Эффективность рекламы зависит от типа дня. Результаты вычислений могут быть представлены в виде следующей таблицы: Таблица 8.13 Результаты анализа
Использованы следующие обозначения:  – сумма квадратов для фактора А; – сумма квадратов для фактора В; – сумма квадратов для взаимодействия факторов; – сумма квадратов для ошибки;а – количество уровней фактора А; b – количество уровней фактора В; n – количество объектов в каждой группе. Общая изменчивость в двухфакторном дисперсионном анализе может быть разложена следующим образом: 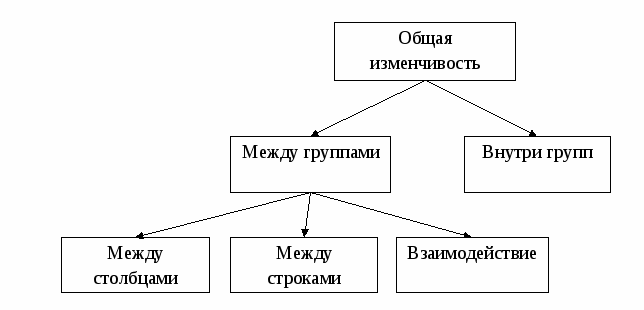 Рис.8.7 Распределение изменчивости Статистическая проверка гипотезы о наличии различий осуществляется на основании  – статистики:  ,  ; ,  ; ,  Условия применения 1. Генеральные совокупности, из которых извлечены выборки, должны быть нормально распределены. 2. Выборки должны быть независимыми. 3. Дисперсии генеральных совокупностей, из которых извлекались выборки, должны быть равными. 4. Группы должны иметь одинаковый объем выборки. 8.6 Пример использования двухфакторного дисперсионного анализа Необходимо выяснить, оказывают ли влияние тип потребляемого бензина и тип автомобиля на расход топлива. Для этого будут использованы два типа бензина – обычный и высокооктановый, и для каждой группы будут использованы два типа автомобилей – с двумя ведущими колесами и с четырьмя. Для каждой группы будут использованы по два автомобиля, всего восемь. Таблица 8.14 Пробег автомобиля в милях на галлон
Алгоритм решения задачи:
Формулировка гипотез.
Н0: Тип топлива и тип автомобиля не оказывают эффекта взаимодействия на потребление бензина. Н1: Тип топлива и тип автомобиля оказывают эффекта взаимодействия на потребление бензина.
Н0: Для двух типов топлива нет разницы между средним потреблением бензина. Н1: Для двух типов топлива существует разница между средним потреблением бензина.
Н0: Для автомобилей с двумя и четырьмя ведущими колесами нет разницы в среднем потреблении бензина. Н1: Для автомобилей с двумя и четырьмя ведущими колесами существует разница в среднем потреблении бензина. Каждая независимая переменная, или фактор, имеет два уровня (принимает два значения). Фактор А - тип топлива: обычное и высокооктановое, а = 2. Фактор В - тип автомобиля: также имеет два значения, b = 2. Число объектов в каждой группе, n = 2. Степени свободы для каждого фактора:
Критические значения:  ; ; .Если факторы имеют различное число градаций, критические значения будут различными. Таблица 8.15 Результаты дисперсионного анализа
Поскольку  ,  , что превышает критический уровень 7,71, нулевые гипотезы об отсутствии влияния эффекта взаимодействия и типа автомобиля отвергаются. Можно сделать вывод о том, что тип автомобиля и сочетание типа топлива и типа автомобиля оказывает существенное влияние на потребление топлива.8.6 Анализ взаимодействия Влияние каждого фактора называют основными или главными эффектами. Если нет значимого эффекта взаимодействия, основные эффекты можно интерпретировать независимо друг от друга. Однако, если значимый эффект взаимодействия существует, надо более внимательно интерпретировать основные эффекты. Чтобы интерпретировать результаты двухфакторного дисперсионного анализа, можно использовать график, на который наносятся средние значения каждой группы. Рассмотрим пример, рассматривающий влияние типа бензина и типа автомобиля на расход топлива. В таблице приведены средние значения пробега. Таблица 8.16 Средний пробег автомобиля в милях на галлон топлива
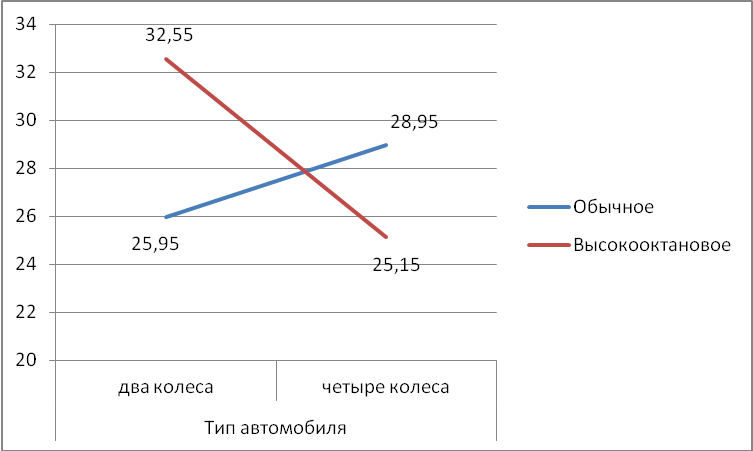 Рис. 8.8 Беспорядочное взаимодействие На графике (рис 8.8) прямые, соединяющие соответствующие средние, пересекаются. В случае такого пересечения и при значительном эффекте взаимодействия, это взаимодействие называется беспорядочным. В случае беспорядочного взаимодействия не следует интерпретировать основные эффекты без учета эффекта взаимодействия. Другой возможный тип взаимодействия – порядковое взаимодействие (рис.8.9). Если значение F-критерия для взаимодействия оказывается значимым и прямые не пересекаются, тогда взаимодействие называется порядковым, и основные эффекты можно интерпретировать отдельно друг от друга. 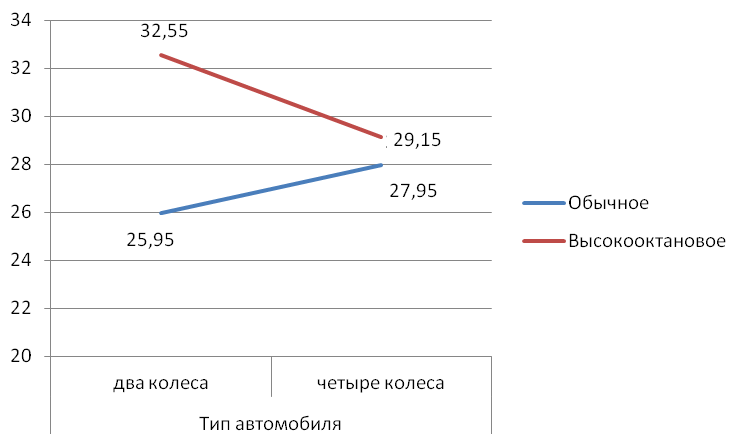 Рис.8.9 Порядковое взаимодействие Наконец, когда нет значительного эффекта взаимодействия, прямые на графике будут параллельными или почти параллельными (рис.8.10). В подобной ситуации основные эффекты можно интерпретировать независимо друг от друга, поскольку не существует значимого взаимодействия. На рисунке приведен график двух переменных, когда эффект взаимодействия незначителен, прямые практически параллельны. 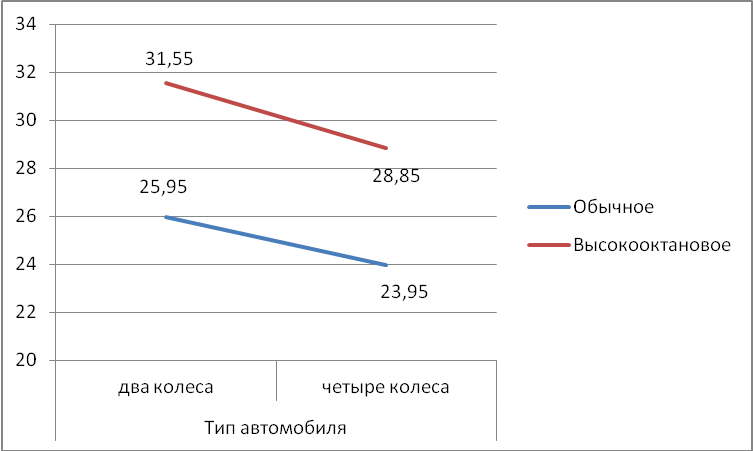 Рис.8.10 Отсутствие значимого взаимодействия Многомерный ANOVA (MANOVA) MANOVA применяется для изучения эффектов влияния факторов не на одну, а на несколько переменных (многомерную зависимую переменную). Таким образом, для каждого объекта имеются несколько зависимых переменных, которые подвергаются дисперсионному анализу. MANOVA позволяет проверить не только гипотезы о влиянии факторов на каждую зависимую переменную в отдельности, но и гипотезу о влиянии факторов на всю совокупность зависимых переменных, как на одну многомерную переменную. Однако MANOVA может применяться как альтернатива ANOVA с повторными измерениями в случае, если не выполняется ее основное допущение о сферичности ковариационно-дисперсионной матрицы. Однако следует учитывать, что MANOVA является менее мощной, но более сложной процедурой, особенно для выборок небольшой численности. 8.7 Примеры задач, решаемых с использованием дисперсионного анализа В задачах, которые решаются с использованием дисперсионного анализа, присутствует результативный признак числовой природы, на который воздействует одна или несколько переменных, имеющих номинальную природу. Например, несколько видов рационов откорма скота или два способа их содержания и т.п. Пример 1. В течение недели в трех разных местах работало несколько аптечных киосков. В дальнейшем мы можем оставить только один. Необходимо определить, существует ли статистически значимое отличие между объемами реализации препаратов в киосках. Если да, мы выберем киоск с наибольшим среднесуточным объемом реализации. Если же разница объема реализации окажется статистически незначимой, то основанием для выбора киоска должны быть другие показатели. Пример 2. Сравнение контрастов групповых средних. Семь политических пристрастий упорядочены от крайне либеральные до крайне консервативных, и линейный контраст используется для проверки того, есть ли отличная от нуля тенденция к возрастанию средних значений по группам - т. е. есть ли значимое линейное увеличение среднего возраста при рассмотрении групп, упорядоченных в направлении от либеральных до консервативных. Пример 3. Двухфакторный дисперсионный анализ. На количество продаж товара, помимо размеров магазина, часто влияет расположение полок с товаром. Данный пример содержит показатели недельных продаж, характеризуемые четырьмя типами расположения полок и тремя размерами магазинов. Результаты анализа показывают, что оба фактора – расположение полок с товаром и размер магазина – влияют на количество продаж, однако их взаимодействие значимым не является. Пример 4. Исследуется влияние на припек хлеба (превышение массы печёного хлеба по сравнению с массой употреблённой муки) всех возможных комбинаций трех жиров и трех рыхлителей теста. Необходимо выявить значимость взаимодействия жир-рыхлитель. После этого определить различные возможности выбора контрастов, позволяющих выяснить, какие именно комбинации уровней факторов различаются. Пример 5. Одномерный анализ повторных измерений. Этот эксперимент проводился для определения влияния индивидуального рейтинга тревожности на сдачу экзамена в четырех последовательных попытках. Данные организованы так, чтобы их можно было рассматривать как группы подмножеств всего множества данных. Эффект тревожности оказался незначимым, а эффект попытки - значим. | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
;
;
;
;