8_ Дисперсионный анализ-1. 8. Дисперсионный анализ. 1 Понятие, назначение дисперсионного анализа. Виды дисперсионного анализа
 Скачать 0.57 Mb.
|
|
8. Дисперсионный анализ. 8.1 Понятие, назначение дисперсионного анализа. Виды дисперсионного анализа. Дисперсионный анализ – анализ изменчивости результативного признака под влиянием каких-либо контролируемых переменных факторов. (В зарубежной литературе именуется ANOVA – «Analisis of Variance»). Результативный признак называют также зависимым признаком, а влияющие факторы – независимыми признаками. Ограничение метода: независимые признаки могут измеряться по номинальной, порядковой или метрической шкале, зависимые – только по метрической. Для проведения дисперсионного анализа выделяют несколько градаций факторных признаков, а все элементы выборки группируют в соответствии с этими градациями. Формулировка гипотез в дисперсионном анализе. Нулевая гипотеза: «Средние величины результативного признака во всех условиях действия фактора (или градациях фактора) одинаковы». Альтернативная гипотеза: «Средние величины результативного признака в разных условиях действия фактора различны». Дисперсионный анализ можно подразделить на несколько категорий в зависимости: от количества рассматриваемых независимых факторов; от количества результативных переменных, подверженных действию факторов; от характера, природы получения и наличия взаимосвязи сравниваемых выборок значений. При наличии одного фактора, влияние которого исследуется, дисперсионный анализ именуется однофакторным, и распадается на две разновидности: - Анализ несвязанных (то есть – различных) выборок. Например, одна группа респондентов решает задачу в условиях тишины, вторая – в шумной комнате. (В этом случае, к слову, нулевая гипотеза звучала бы так: «среднее время решения задач такого-то типа будет одинаково в тишине и в шумном помещении», то есть не зависит от фактора шума.) - Анализ связанных выборок, то есть, двух замеров, проведенных на одной и той же группе респондентов в разных условиях. Тот же пример: в первый раз задача решалась в тишине, второй – сходная задача – в условиях шумовых помех. (На практике к подобным опытам следует подходить с осторожностью, поскольку в действие может вступить неучтенный фактор «научаемость», влияние которого исследователь рискует приписать изменению условий, а именно, - шуму.) В случае если исследуется одновременное воздействие двух или более факторов, мы имеем дело с многофакторным дисперсионным анализом, который также можно подразделить по типу выборки. Если же воздействию факторов подвержено несколько переменных, - речь идет о многомерном анализе. Проведение многомерного дисперсионного анализа предпочтительнее одномерного только в том случае, когда зависимые переменные не являются независимыми друг от друга и коррелируют между собой. Обобщенно задача дисперсионного анализа состоит в том, чтобы из общей вариативности признака выделить три частные вариативности:
Для оценки вариативности, обусловленной действием исследуемых переменных и их взаимодействием вычисляется отношение соответствующего показателя вариативности и случайной вариативности. Показателем этого соотношения является F – критерий Фишера.  ; ; .Чем в большей степени вариативность признака обусловлена действием влияющих факторов или их взаимодействием, тем выше эмпирические значения критерия  .В формулу расчета критерия входят оценки дисперсий, и, следовательно, этот метод относится к разряду параметрических. Непараметрическим аналогом однофакторного дисперсионного анализа для независимых выборок является критерий Краскела-Уоллеса. Он подобен критерию Манна-Уитни для двух независимых выборок, за тем исключением, что он суммирует ранги для каждой из  групп.Кроме этого, в дисперсионном анализе может быть применен медианный критерий. При его использовании для каждой группы определяются число наблюдений, которые превышают медиану, вычисленную по всем группам, и число наблюдений, которые меньше медианы, после чего строится двумерная таблица сопряженности. Критерий Фридмана является непараметрическим обобщением парного t-критерия для случая выборок с повторными измерениями, когда количество сравниваемых переменных больше двух. В отличие от корреляционного анализа, в дисперсионном анализе исследователь исходит из предположения, что одни переменные выступают как влияющие (именуемые факторами или независимыми переменными), а другие (результативные признаки или зависимые переменные) – подвержены влиянию этих факторов. Хотя такое допущение и лежит в основе математических процедур расчета, оно, однако, требует осторожности при выводах о причине и следствии. Например, если мы выдвигаем гипотезу о зависимости успешности работы должностного лица от фактора Н (социальной смелости по Кэттелу), то не исключено обратное: социальная смелость респондента как раз и может возникнуть (усилиться) вследствие успешности его работы – это с одной стороны. С другой: следует отдать себе отчет в том, как именно измерялась «успешность»? Если за ее основу взяты были не объективные характеристики (модные нынче «объемы продаж» и проч.), а экспертные оценки сослуживцев, то имеется вероятность того, что «успешность» может быть подменена поведенческими или личностными характеристиками (волевыми, коммуникативными, внешними проявлениями агрессивности etc.). 8.2 Постановка задачи дисперсионного анализа. Представим смысл дисперсионного анализа графически. 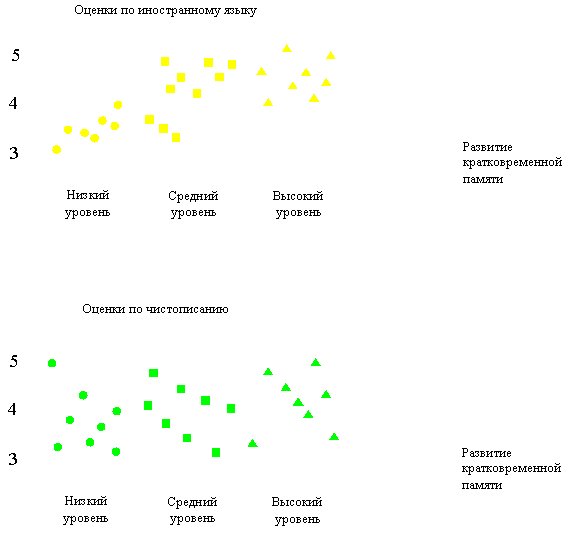 Рис 8.1 Влияние кратковременной памяти на успеваемость В примере (рис 8.1) иллюстрируется исследование зависимости успеваемости школьников от развития кратковременной памяти. В качестве независимого фактора рассматривается уровень развития кратковременной памяти, а в качестве результативных признаков – успеваемость по предмету. Видно, например, что фактор, по-видимому, оказывает существенное влияние при обучении иностранному языку, и незначим для чистописания, что, впрочем, вполне согласуется со здравым смыслом. В качестве примера постановки задачи рассмотрим задачу анализа влияния условий выращивания на вес томатов. Имеются данные о весе томатов (все растение целиком; кг), которые выращивали в течение 2 месяцев при трех разных экспериментальных условиях :
Таблица 8.1 Исходные данные
Переменная «условия» представляет собой фактор с тремя уровнями. 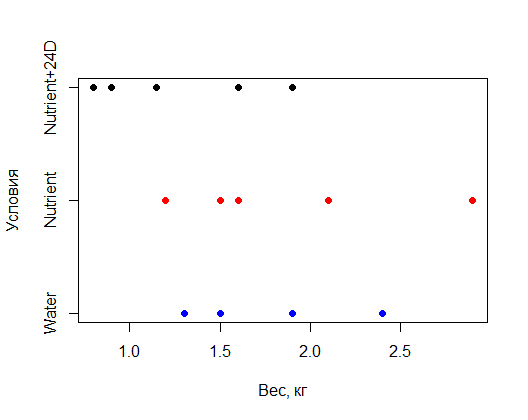 Рис. 8.2. Результаты измерений веса растений томатов, выращенных при разных экспериментальных условиях Из рис. 8.2 видно, что измеренные значения веса растений достаточно близки для всех трех экспериментальных условий, хотя и есть некоторая тенденция к снижению веса в группе "Nutrient+24D". Это визуальное впечатление подтверждается рассчитанными групповыми средними (таблица 8.2): Таблица 8.2 Средний вес растений, выращенных в различных условиях
Подлежащую проверке нулевую гипотезу можно сформулировать так: исследованные условия выращивания растений не оказывают никакого влияния на вес последних. Другими словами, нулевая гипотеза утверждает, что наблюдаемые различия между групповыми средними несущественны и вызваны влиянием случайных факторов, т.е. все полученные измерения веса растений происходят из одной нормально распределенной генеральной совокупности.  Рассматриваемый пример соответствует случаю однофакторного дисперсионного анализа: изучается действие одного фактора - условий выращивания (с тремя уровнями - Water, Nutrient и Nutrient+24D) на интересующую нас зависимую переменную-отклик - вес растений. К сожалению, исследователь почти никогда не имеет возможности изучить всю генеральную совокупность. Чтобы узнать, верна ли приведенная выше нулевая гипотеза, рассматривается вопрос: какова вероятность получить наблюдаемые различия между групповыми средними, если группы – это случайные выборки из одной нормально распределенной генеральной совокупности? Для ответа на этот вопрос потребуется статистический критерий, который количественно характеризовал бы величину различий между сравниваемыми группами. Очевидно, до проверки гипотезы есть смысл убедиться в целесообразности такой проверки: действительно ли различия между группами могут быть неслучайными. На рис. 8.3 к исходным данным добавлена еще одна группа - из точек, соответствующих выборочным средним (Means) . 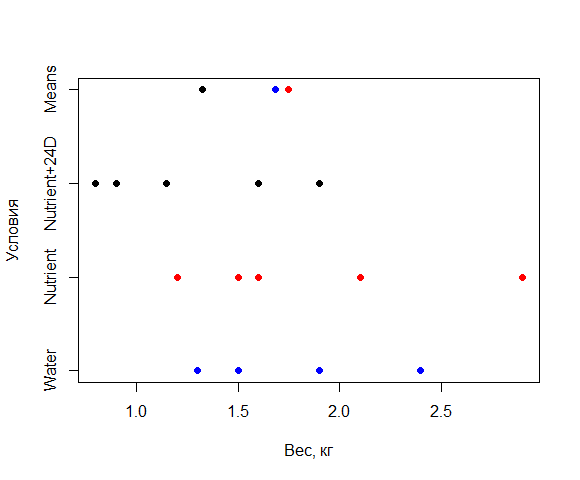 Рис. 8.3 Вес растений, выращенных при разных условиях и средних значений каждой экспериментальной группы Из рис. 8.3 видно, что различия средних не слишком значительны. Разброс средних меньше, чем разброс внутри групп. На рис.8.4 приведен пример данных, для которых различия более очевидны. 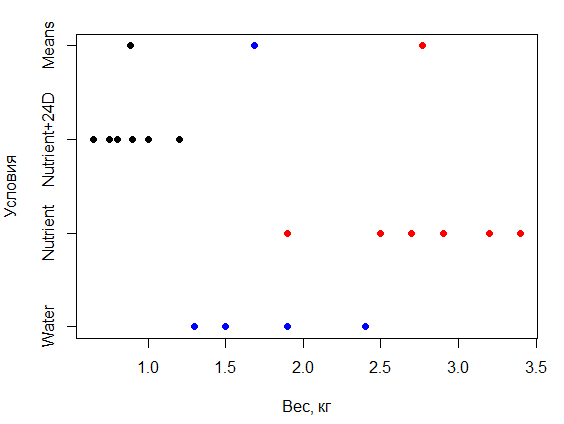 Рис. 8.4 Вес растений, выращенных при разных условиях и средних значений каждой группы (при измененных исходных данных) На рис. 8.4 по сравнению с рис. 8.3 - группы точек, отражающих экспериментальные данные, оказались значительно раздвинутыми вдоль оси. Результатом этого стало значительное различие групповых средних: разброс групповых средних на рис. 8.4 в целом превышает разброс значений в экспериментальных группах. Следовательно, для оценки различий между группами следует сравнить разброс групповых средних с разбросом значений внутри групп. 8.3 Однофакторный дисперсионный анализ Дисперсионный анализ, который рассматривает только одну независимую переменную называется однофакторным дисперсионным анализом (One-Way ANOVA). Однофакторный дисперсионный анализ (ANOVA – analysis of variance) используется для сравнения средних значений для трех и более выборок (групп). Каждая выборка (группа) соответствует одной из градаций независимой переменной (фактора). Фактор имеет несколько значений – уровней фактора. Например, фактором может быть уровень образования, вид деятельности, возрастная группа респондентов, степень лояльности к торговой марке и т.д. Анализ основан на расчете 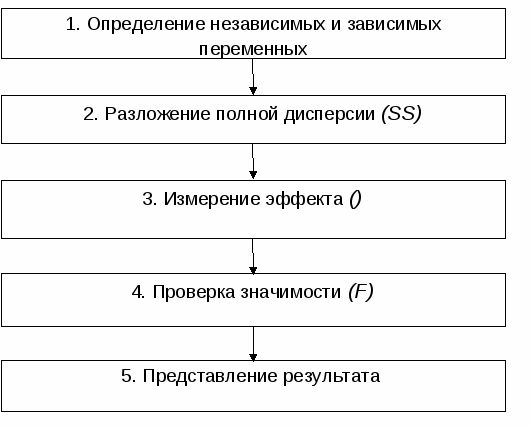 -статистики (статистика Фишера), которая представляет собой отношение двух дисперсий: межгрупповой и внутригрупповой. -тест в однофакторном дисперсионном анализе устанавливает, значимо ли отличаются средние нескольких независимых выборок. Он заменяет  -тест для независимых выборок при наличии более двух выборок и дает тот же результат в случае двух выборок. Рис. 8.5 Процедура выполнения однофакторного дисперсионного анализа Таким образом, набор данных в ANOVA состоит из – независимых одномерных выборок, элементы которых измерены в одинаковых единицах (долл, кг, баллы, пр.). Выборки не обязаны иметь одинаковый объем. Подготовленные данные удобно представлять в виде таблицы (табл. 8.3). Таблица 8.3 Данные подготовленные для анализа
Всего проведено  измерений, которые разделены на групп – по числу уровней фактора. Условия применения -статистики1. Генеральные совокупности, из которых формируются выборки, должны быть нормально распределены. 2. Выборки должны быть независимы. 3. Дисперсии генеральных совокупностей должны быть равны. Нулевая гипотеза в однофакторном дисперсионном анализе утверждает, что все средние значения из различных генеральных совокупностей (которые представлены выборочными средними) равны между собой.  – все средние равны;Альтернативная гипотеза утверждает, что хотя бы два любых средних не равны между собой.  не все средние равны.Для изучения различий между зависимыми переменными проводится разложение полной дисперсии:  ,где  – межгрупповая вариация; – внутригрупповая вариация.Межгрупповая вариация  показывает, насколько выборочные средние отличаются между собой. Она равна нулю, если средние равны и тем больше, чем сильнее различаются средние. Межгрупповая вариация рассчитывается как сумма квадратов отклонений групповых средних от общей средней: Т  огда межгрупповая (факторная) дисперсия может быть рассчитана как средний квадрат:  Внутригрупповая вариация  показывает, насколько отличаются между собой значения внутри выборок, и рассчитывается как сумма внутригрупповых квадратов отклонений: Внутригрупповая (остаточная) дисперсия может быть рассчитана как  Общая сумма квадратов отклонений  Результаты вычислений можно представить в виде следующей таблицы: Таблица 8.4 Результаты анализа
Степень влияния независимой переменной на зависимую переменную оценивается при помощи коэффициента детерминации  или корреляционного отношения  (эта). Корреляционное отношение: Значение корреляционного отношения находится в пределах от 0 до 1. Оно равно 0, когда все выборочные средние равны, т.е. независимая переменная не влияет на зависимую, и, наоборот, влияние увеличивается с ростом этого значения. Другими словами, показатели и представляет собой меру вариации зависимой переменной, вызванную влиянием на нее независимой переменной (фактора).Статистическая проверка гипотезы о равенстве средних (наличии различий) осуществляется на основании – статистики:  .Найденное расчетное значение критерия сравнивается с расчетным. Чтобы найти критическое значение, необходимо учесть число степеней свободы (df – degree freedom) и соответствующий уровень значимости (по умолчанию 5%). Если разницы в средних нет, то отношение оценок межгрупповой и внутригрупповой дисперсий – расчетное значение -критерия – не превышает критического значения -критерия и нулевая гипотеза не отвергается.В противном случае расчетное значение больше критического:  .Такой результат является значимым, что говорит о наличии существенных различий между средними значениями по группам. При этом нулевая гипотеза отвергается. Проверку гипотезы можно также осуществлять на основании достигнутого уровня значимости  , который сравнивают с выбранным уровнем значимости, например с 5%. Если достигнутый уровень значимости превышает выбранный уровень значимости (например,  ), то нулевая гипотеза не отвергается Поскольку при проверке гипотезы производится сравнение дисперсий, метод и получил название дисперсионный анализ. | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
