8. Классификация форм взаимосвязей. Методы выявления зависимостей
 Скачать 233.6 Kb. Скачать 233.6 Kb.
|
|
8. Классификация форм взаимосвязей. Методы выявления зависимостей. В статистике принято различать следующие виды зависимости: 1. парная корреляция – связь между 2мя признаками результативным и факторным, либо между двумя факторными. 2. частная корреляция – зависимость между результативным и одним факторным признаком при фиксированном значении другого факторного признака. 3. множественная корреляция – зависимость результативного признака от двух и более факторных признаков включенных в исследование. Задачей корреляционного анализа является количественная оценка тесноты связи между признаками В конце 19 века Гальтон и Пирсон исследовали зависимость между ростом отцов и детей. Регрессия исследует форму связи. Задача регрессионного анализа – определение аналитического выражения связи. Регрессионный анализ заключается в определении аналитического выражения связи. По форме различают линейную регрессию, которая выражается уравнением прямой 19. Аддитивная модель: методика расчета и прогнозирование Современные условия, в которых осуществляется производственно-коммерческая деятельность предприятия, не всегда позволяют рассчитывать на значительные вложения в расширение материально-технической базы. Поэтому на передний план выдвигается задача наиболее эффективного использования имеющихся ресурсов организации через реализацию изложенных принципов планирования (принцип научности, оптимизации, сбалансированности) на основе системного подхода и широкого применения экономико-математических методов. Разработка и применение экономико-математических методов и моделей в планировании позволяет повысить научность принимаемых плановых решений, учесть большое количество взаимосвязанных факторов, обеспечить многовариантность плановых расчетов, находить оптимальные варианты планов деятельности хозяйственного субъекта. Как правило, каждое предприятие явно или не явно в различных областях своей деятельности использует прогнозы. Так как планировать будущий исход в условиях неопределенности и выбирать путь, оказывающий влияние на будущее - задача, стоящая перед менеджерами компании. И целью любого прогноза является уменьшение того уровня неопределенности, в пределах которого приходится принимать решение. Практически все методы прогнозирования основаны на признании факта существования определенной зависимости (функции или константы) происходящих изменений показателей финансово-хозяйственной деятельности от одного отчетного периода к другому. Но в действительности, подобные предположения о том, что условия, породившие полученные данные, неотличимы от условий будущего, не выполняются в полной мере. Поэтому, только сочетая формализованные и неформализованные методы прогнозирования и планирования, можно составлять более точные, своевременные и понятные прогнозы, воспринимаемые как инструмент, используемый для принятия решения. На сегодняшний день наука достаточно далеко продвинулась в разработке технологий прогнозирования. Наиболее известными являются методы линейного программирования, линейной регрессии, модель экспоненциального сглаживания и другие. Разработаны соответствующие программы, но в тоже время, чтобы осознать и оценить процесс формирования прогноза самостоятельно, можно использовать методы, реализуя несложные алгоритмы в MS Excel. Для прогнозирования объема продаж, темпа инфляции и других показателей макро и микроэкономической конъюнктуры, и при наличии временных рядов обычно используются аддитивные и мультипликативные модели прогнозирования. Анализ аддитивной модели. Данную модель можно представить в виде формулы: А = T S E где: А - прогнозируемое значение; Т - тренд. Трендом называется общее изменение со временем результативного признака. S - сезонная компонента. Сезонная вариация - это повторение данных через небольшой промежуток времени. Под сезоном можно понимать и день, и неделю, и месяц, и квартал. Е - ошибка прогноза. Величины ошибок вычисляются по уравнению тренда и прошлым данным, и позволяют оценить качество прогноза. Рассмотрим на примере составление прогноза объема продаж на следующие два квартала, на основании данных за последние 11 кварталов. Как правило, для формирования аддитивной модели предлагается следующий алгоритм: 1. Исключить влияние сезонной вариации, используя метод скользящей средней. 2. Проводится десезонализация данных, которая заключается в вычитании сезонной компоненты из фактических значений в расчете тренда на основе полученных десезонализированных данных. 3. Расчет ошибок как разности между фактическими и трендовыми значениями. 4. Расчет среднего отклонения или среднеквадратической ошибки для сопоставления модели с реальной ситуацией или для выбора наилучшей модели. Но упростим задание, приняв, что в данном примере значение сезонной вариации является не значительным. На первом этапе рассчитаем трендовое значение объема продаж. Уравнение линии тренда: Т=a b*x Для этого необходимо предварительно рассчитать следующие значения в 3-м и 4-м столбцах таблицы. 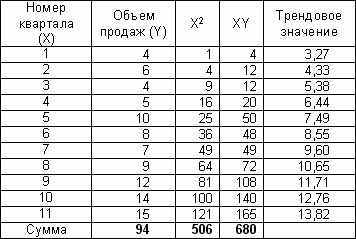 Таблица расчета трендового значения 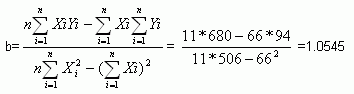 Формула расчета коэффициента b 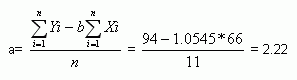 Формула расчета коэффициента a Подставляя в формулу рассчитанные значения коэффициентов а и b, получаем трендовое значение объема продаж = 2,22 1.0545 * номер квартала. Для первого квартала трендовое значение получается 2,22 1,0545*1=3,27 тыс.руб. Считая, что тенденция, выявленная по прошлым данным, сохранится и в ближайшем будущем. Прогноз объем а продаж в 12-м квартале составит: 2,22 1,0545*12=14,8 тыс.руб. Прогноз объема продаж в 13-м квартале: 2,22 1,0545*13=15,9 тыс.руб. Но вместо вычислений коэффициентов a и b и трендового значения по формулам можно воспользоваться статистическими функциями, представленными в электронных таблицах Microsoft Excel: ОТРЕЗОК (известные_значения_y;известные_значения_x) Вычисляет точку пересечения линии с осью y, используя известные_значения_x и известные_значения_y. Точка пересечения находится на оптимальной линии регрессии, проведенной через известные_значения_x и известные_значения_y. Функция ОТРЕЗОК используется, когда нужно определить значение зависимой переменной при значении независимой переменной, равном 0 (нулю). НАКЛОН (известные_значения_y;известные_значения_x) Возвращает наклон линии линейной регрессии для точек данных в аргументах известные_значения_y и известные_значения_x. Наклон определяется как частное от деления расстояния по вертикали на расстояние по горизонтали между двумя любыми точками прямой, то есть наклон - это скорость изменения значений вдоль прямой. ТЕНДЕНЦИЯ (известные_значения_y;известные_значения_x;новые_значения_x;конст) Возвращает значения в соответствии с линейным трендом. Аппроксимирует прямой линией (по методу наименьших квадратов) массивы известные_значения_y и известные_значения_x. Возвращает значения y, в соответствии с этой прямой для заданного массива новые_значения_x. 28. Прогнозирование в менеджменте Под прогнозированием понимается процесс исследования, направленный на выявление тенденций развития организации и ее внешнего окружения. Целью прогнозирования, прежде всего, является побуждение к размышлению о том, что может произойти во внешней среде и к каким последствиям для организации это приведет. Прогнозирование позволяет оптимизировать деятельность компании, более точно распределить ресурсы. На основе прогнозов строится все планирование производственной и финансовой деятельности организации. В соответствии с прогнозами принимаются решения: - о том, куда и в каких объемах направлять инвестиции, - какие дополнительные производственные мощности потребуются и через какой период времени (например, операторы сотовой связи на основании прогнозов принимают решения об увеличении кол-ва базовых станций, контроллеров, коммутаторов и других элементов сети); - какие технологии и услуги необходимо реализовать, чтобы успешно действовать на рынке в условиях жесткой конкуренции. Прогнозирование повышает бдительность менеджеров и, следовательно, их способность реагировать на изменения. Результатом данного этапа является некое научно обоснованное предположение о состоянии системы управления в будущем (прогноз). Для того, чтобы успешно выполнять эту функцию необходимо знать: - какие существуют методы прогнозирования, - уметь применить соответствующую технику расчетов, - преимущества и ограничения каждого из них, - когда какие методы лучше применять. Под методами прогнозирования понимается совокупность приемов, позволяющих на основе анализа ретроспективных данных, а также внешних и внутренних связей объекта прогнозирования вывести суждения определенной достоверности относительно его будущего развития. Важно, чтобы в компании процесс прогнозирования был определенным образом ФОРМАЛИЗОВАН, т.е. должна быть описана методика его разработки, последовательность прохождения по всем подразделениям с четким указанием применяемых методов построения прогноза, сроков и форм подачи информации. Если это не сделано, то процесс прогнозирования будет происходить стихийно. Выявляя отклонения прогнозных значений от фактических, мы не сможем определить, почему так произошло, соответственно, не сможем сделать выводов для недопущения этих ошибок в будущем, для повышения точности прогнозирования. 2.2 Виды прогнозов
Выбор метода прогнозирования зависит от множества факторов. Отметим некоторые из них: наличие данных, желаемая точность прогноза, а также временные и стоимостные затраты на его составление. Методы прогнозирования условно можно разбить на две группы: количественные, качественные. Количественные методы прогнозирования требуют значительного количества исходных данных и при их отсутствии не могут быть использованы. Качественные методы, наоборот, предназначены для использования в условиях отсутствия достоверной количественной информации. Задание 2. По приведенным в таблицах данным построить диаграммы, показывающие зависимость каждого из показателей от времени (x – t, y – t) и друг от друга (х – у). По каждой диаграмме определить вид зависимости и рассчитать коэффициенты корреляции и детерминации. Сделать выводы. Таблица 4.8 Данные об уровне рентабельности сельхозпредприятий (Х) и размерах среднемесячной заработной платы работников (Y)
Решение: Построим диаграммы, показывающие зависимость каждого из показателей от времени (x – t, y – t) и друг от друга (х – у).  Динамика уровня рентабельности деятельности сельхозпредприятий, % На диаграмме прослеживается нелинейная (полиномиальная) зависимость между показателями. 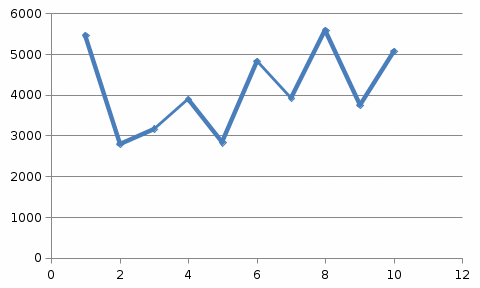 Динамика среднемесячной начисленной заработной платы работающих, руб. На диаграмме прослеживается нелинейная (полиномиальная) зависимость между показателями. 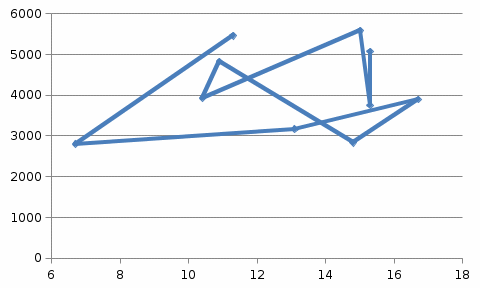 Зависимость между уровнем рентабельности деятельности сельхозпредприятий, % к среднемесячной начисленной заработной платы работающих, руб. На диаграмме прослеживается нелинейная (полиномиальная) зависимость между показателями. Для расчета коэффициентов корреляции составим вспомогательную таблицу Таблица вспомогательных расчетов
Коэффициент корреляции между временем и уровнем рентабельности деятельности сельхозпредприятий определим по формуле (в качестве факторного признака Х выступает номер года t):  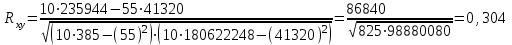 Rxy=0,304 Следовательно, связь между временем и уровнем рентабельности деятельности сельхозпредприятий прямая, т.к. Rxy > 0, а теснота связи умеренная (по шкале Чеддока). Коэффициент детерминации равен R2xy = (0,304)2 = 0,092 или (9,2%). Следовательно, 9,2% изменений уровня рентабельности деятельности сельхозпредприятий объясняется изменением времени. Коэффициент корреляции между временем и среднемесячной начисленной заработной платой работающих по формуле (в качестве факторного признака Х выступает номер года t, а в качестве результативного признака Y выступает Х):  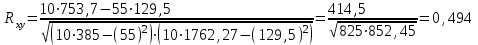 Rxy = 0,494 Следовательно, связь между временем и среднемесячной начисленной заработной платой работающих прямая, т.к. Rxy< 0, а теснота связи умеренная (по шкале Чеддока). Коэффициент детерминации равен R2xy = (0,494)2 = 0,244 (24,4%). Следовательно, 24,4% изменений среднемесячной начисленной заработной платой работающих объясняется изменением времени. Коэффициент корреляции между уровнем рентабельности деятельности сельхозпредприятий и среднемесячной начисленной заработной платой работающих определим по формуле:  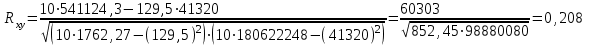 Rxy = 0,208 Следовательно, связь между уровнем рентабельности и среднемесячной начисленной заработной платой работающих прямая, т.к. Rxy< 0, а теснота связи слабая (по шкале Чеддока). Коэффициент детерминации равен R2xy = (0,208)2 = 0,043 (4,3%). Следовательно, 4,3% изменений заработной платой работающих объясняется изменением уровня рентабельности деятельности сельхозпредприятий. Таблица 4.6 Данные об уровне рентабельности и урожайности зерновых культур в регионе
Решение: Построим диаграммы, показывающие зависимость каждого из показателей от времени (x – t, y – t) и друг от друга (х – у). 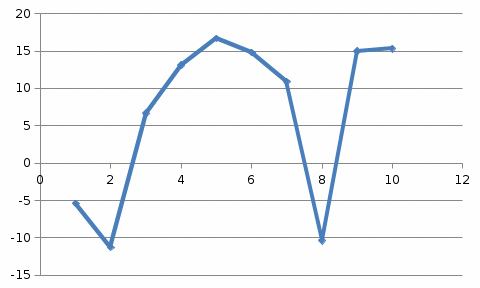 Динамика рентабельности деятельности сельхозпредприятий, %, % На диаграмме прослеживается нелинейная (полиномиальная) зависимость между показателями. 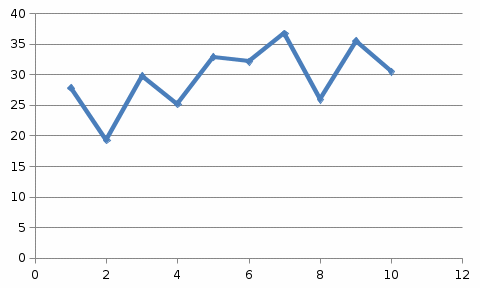 Урожайность зерновых культур в сельхозпредприятиях, ц/га. На диаграмме прослеживается нелинейная (полиномиальная) зависимость между показателями. 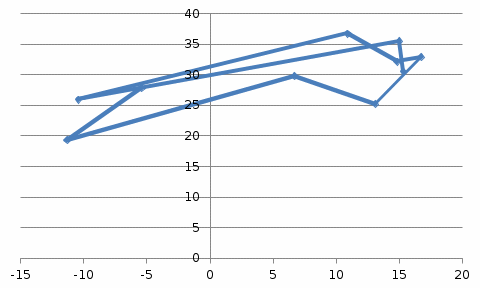 Зависимость между уровнем рентабельности деятельности сельхозпредприятий, % к урожайности зерновых культур в сельхозпредприятиях, ц/га На диаграмме прослеживается нелинейная (полиномиальная) зависимость между показателями. Для расчета коэффициентов корреляции составим вспомогательную таблицу Таблица вспомогательных расчетов
Коэффициент корреляции между временем и урожайности зерновых культур определим по формуле (в качестве факторного признака Х выступает номер года t):  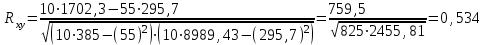 Rxy=0,534 Следовательно, связь между временем и урожайности зерновых культур прямая, т.к. Rxy > 0, а теснота связи заметная (по шкале Чеддока). Коэффициент детерминации равен R2xy = (0,534)2 = 0,285 или (28,5%). Следовательно, 28,5% изменений падежом скота объясняется изменением времени. Коэффициент корреляции между временем и уровнем рентабельности по формуле (в качестве факторного признака Х выступает номер года t, а в качестве результативного признака Y выступает Х):  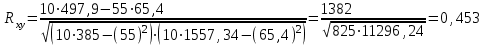 Rxy = 0,453 Следовательно, связь между временем и уровнем рентабельности прямая, т.к. Rxy< 0, а теснота связи умеренная (по шкале Чеддока). Коэффициент детерминации равен R2xy = (0,453)2 = 0,205 (20,5%). Следовательно, 20,5% изменений уровня рентабельности объясняется изменением времени. Коэффициент корреляции между уровнем рентабельности и урожайности зерновых культур определим по формуле:  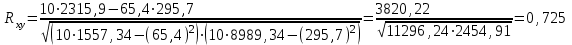 Rxy = 0,725 Следовательно, связь между уровнем рентабельности и урожайности зерновых культур прямая, т.к. Rxy< 0, а теснота связи высокая (по шкале Чеддока). Коэффициент детерминации равен R2xy = (0,725)2 = 0,526 (52,6%). Следовательно, 52,6% изменений урожайности зерновых культур объясняется изменением уровня рентабельности. 2) Анализ по данным об уровне рентабельности и урожайности зерновых культур в регионе 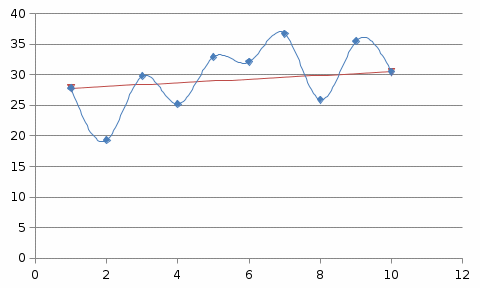 Динамика урожайности зерновых культур в сельскохозяйственных предприятиях На диаграмме прослеживается нелинейная (полиномиальная) между показателями. 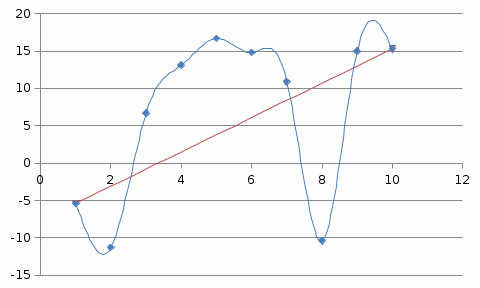 Динамика уровня рентабельности деятельности сельхозпредприятий На диаграмме прослеживается нелинейная (полиномиальная) зависимость между показателями. 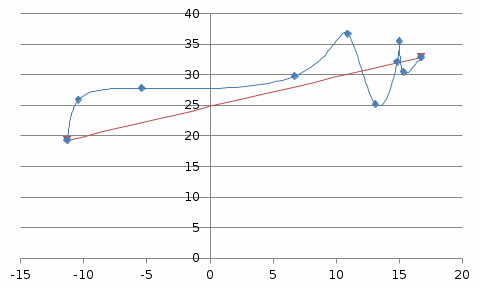 Зависимость между урожайностью зерновых культур от уровня рентабельности сельхозпредприятий На диаграмме прослеживается нелинейная (полиномиальная) зависимость между показателями. Для расчета коэффициентов корреляции составим вспомогательную таблицу Таблица вспомогательных расчетов
Коэффициент корреляции между временем и урожайностью зерновых культур в сельхозпредприятиях определим по формуле (в качестве факторного признака Х выступает номер года t):  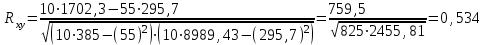 Rxy=0,534 Следовательно, связь между временем и продукцией сельского хозяйства по региону - прямая, т.к. Rxy > 0, а теснота связи умеренная (по шкале Чеддока). Коэффициент детерминации равен R2xy = (0,334)2 = 0,2851 или (28,51%). Следовательно, 28,51% изменений урожайность зерновых культур в сельхозпредприятиях объясняется изменением времени. Коэффициент корреляции между временем и уровнем рентабельности деятельности сельхозпредприятий определим по формуле (в качестве факторного признака Х выступает номер года t, а в качестве результативного признака Y выступает Х):  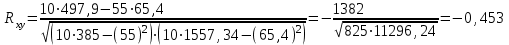 Rxy = -0,453 Следовательно, связь между временем и уровнем рентабельности деятельности сельхозпредприятий обратная, т.к. Rxy < 0, а теснота связи умеренная (по шкале Чеддока). Коэффициент детерминации равен R2xy = (-0,453)2 = 0,205 (20,5%). Следовательно, 20,5% изменений уровня рентабельности деятельности сельхозпредприятий объясняется изменением времени. Коэффициент корреляции между урожайностью зерновых культур и уровнем рентабельности деятельности сельхозпредприятий определим по формуле:  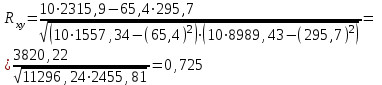 Rxy = 0,725 Следовательно, связь между урожайностью зерновых культур и уровнем рентабельности деятельности сельхозпредприятий прямая, т.к. Rxy > 0, а теснота связи высокая (по шкале Чеддока). Коэффициент детерминации равен R2xy = (0,725)2 = 0,526 (52,6%). Следовательно, 52,6% изменений урожайность зерновых культур объясняется изменением уровня рентабельности деятельности сельхозпредприятий. |
