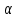8. Классификация форм взаимосвязей. Методы выявления зависимостей
 Скачать 233.6 Kb. Скачать 233.6 Kb.
|
|
Задание 3. Прогнозирование по однофакторным регрессионным моделям По приведенным в табл. данным, построить однофакторную линейная модель типа у=a+bx.
Оцените качество модели с помощью коэффициента детерминации, средней ошибки аппроксимации и F-критерия Фишера. Табличное значение F-критерия Фишера (Fтабл.) равно 10,13 при Р=0,95. Выполнить прогноз на следующие три периода и рассчитать ошибку прогноза, если х изменялся следующим образом:
Сделать выводы. Решение: 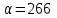 Для построения однофакторной линейной модели типа
Составим и решим систему нормальных уравнений, для нахождения параметров уравнения регрессии. 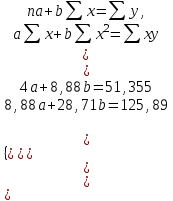 Домножим первое уравнение на 2,22 и вычтем из него 2: 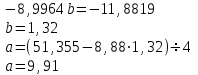 Однофакторная линейная модель примет вид: Экономическая интерпретация, полученной модели: при увеличении фактора х на 1 единицу своего измерения результативный признак Y увеличится на 1,32 единиц своего измерения. Для того чтобы выполнить прогноз по данной модели, необходимо проверить ее качество. Качество регрессионной модели считается высоким, если: коэффициент детерминации больше или равен 0,5; средняя ошибка аппроксимации менее или равна 10%; Fтабл Найдем перечисленные показатели. Для нахождения коэффициента детерминации необходимо знать коэффициент корреляции, который определим по формуле:  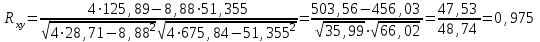 Rxy = 0,975 Следовательно, связь между Y и Х прямая, т.к. Rxy > 0, а теснота связи весьма высокая (по шкале Чеддока). Коэффициент детерминации равен R2xy = (0,975)2 = 0,95 (95,0%). Следовательно, 95,0% изменений результативного признака Y объясняется изменением фактора Х. В нашем случае коэффициент детерминации больше 0,5, следовательно, первое условие, определяющие высокое качество модели выполнилось. Для расчета средней ошибки аппроксимации построим вспомогательную таблицу:
Определим среднюю ошибку аппроксимации по формуле: 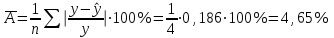 В среднем расчетные значения отклоняются от фактических на 4,65%. Ошибка аппроксимации небольшая (А<8%), регрессионная модель хорошо описывает изучаемую закономерность. Второе условие, определяющее высокое качество модели выполнилось. Определим фактическое значение критерия Фишера по формуле: По условию задачи Fтабл = 10,13 при Р=0,95. 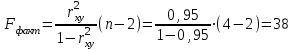 Если Fтабл. Так как, все три условия, определяющих высокое качество модели выполнились, то модель вида Прогнозирование по линейной однофакторной регрессии осуществляется путем подстановки ожидаемого значения х в уравнение регрессии. Определим ожидаемые значения х в прогнозных периодах.
Выполним прогноз на следующие три периода: Рассчитаем ошибки прогноза по формуле: 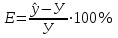 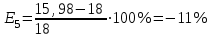 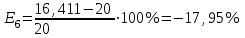 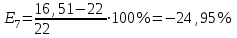 Вывод: Однофакторная линейная модель примет вид: Следовательно, при увеличении фактора х на 1 единицу своего измерения результативный признак Y увеличится на 1,32 единиц своего измерения. Данная модель может быть использована для прогнозирования признака Y от фактора Х, так как выполняются условия, определяющие ее высокое качество. Наиболее точным оказался прогноз на 5-ый период (соответствует минимальное значение ошибки прогноза). Задание 4. Прогнозирование по многофакторным регрессионным моделям По приведенным в табл. 4.12 данным построить уравнение многофакторной линейной регрессии, если а= 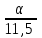 , b1= , b1=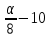 , b2= , b2=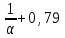 , b3= , b3=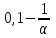 , b4= , b4=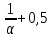 , b5= , b5=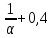 Фактические значения х
Рассчитать значения результативного показателя на следующие 2 периода. На основе матрицы парных коэффициентов корреляции (табл.) (рассчитать) выявить и устранить мультиколлинеарные факторы. После их устранения построить уравнение регрессии по новым данным регрессионного анализа, характеризующее зависимость результирующего показателя (y) от факторных (xi) в линейной форме.
Рассчитать прогнозные значения результативного показателя по скорректированной многофакторной модели на следующие 2 периода, если:
Оценить точность прогноза, рассчитав ошибку прогноза для обоих случаев. Сделать выводы. | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||