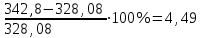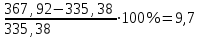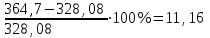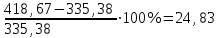8. Классификация форм взаимосвязей. Методы выявления зависимостей
 Скачать 233.6 Kb. Скачать 233.6 Kb.
|
|
Решение: Если а= 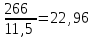 , b1= , b1=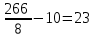 , b2= , b2=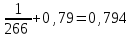 , b3= , b3=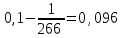 , b4= , b4=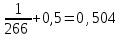 , b5= , b5=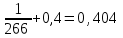 , тогда , тогда1. Уравнение многофакторной регрессии будет выглядеть следующим образом: Рассчитаем прогнозные значения Y:
Определим ошибку прогноза по формуле: 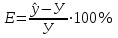 =22,96+23∙118,65+0,794∙84,4+0,096∙64,1+0,504∙15,9+0,404∙3311,45= =3783,04 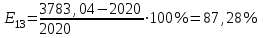 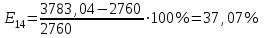 Проверим модель на наличие мультиколлинеарности и при необходимости устраним ее. Найдем пары мультиколлинеарных факторов, которые удовлетворяют условию rхiхj 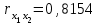 и и 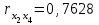 Из каждой пары необходимо исключить фактор, имеющий наименьшее значение rхiy. Рассмотрим первую пару Рассмотрим вторую пару Итак, из модели исключаем х1 и х4, модель примет вид: Рассчитаем скорректированные прогнозные значения Y:
Определим ошибку прогноза по формуле: 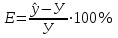 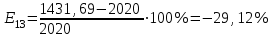 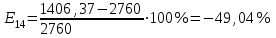 Вывод: Более качественной является пятифакторная регрессионная модель, так как позволяет получить меньшие значения ошибки прогноза. Задание 5. Прогнозирование на основе трендовых моделей Имеются некоторые данные об объеме продаж (д.е.) за 10 лет.
Выполнить прогноз с помощью среднего абсолютного прироста, среднего темпа роста и уравнения тренда на 11-12-ый периоды. Если в 11-м периоде у будет равен (325,7 + 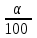 ) д.е., а в 12-м периоде – (333 + ) д.е., а в 12-м периоде – (333 +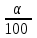 ) д.е., рассчитать ошибку прогноза по каждой из моделей. ) д.е., рассчитать ошибку прогноза по каждой из моделей.Оцените точность прогноза по каждому периоду. Решение: Расчет уравнения тренда ряда динамики объема продаж
Если 1) Прогнозирование с помощью среднего абсолютного прироста. Среднегодовой абсолютный прирост объема продаж: 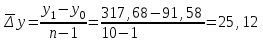 (шт.). (шт.).Тогда, прогноз роста объема продаж: на 2012 г. 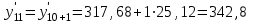 (шт.). (шт.).на 2013 г.: 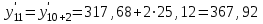 (шт.). (шт.).2) Прогнозирование с помощью среднего темпа роста. Средний темп роста можно рассчитать следующим образом: 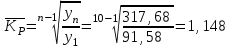 или 114,8% или 114,8%Рассчитаем прогноз объема продаж: на 2012 г.: на 2013 г.: 3) Прогнозирование на основе уравнения тренда. Для прогнозирования по прямой следует получить уравнение: Для расчета параметров а0 и а1 решается система нормальных уравнений:  где n - число уровней ряда динамики, t - условное обозначение фактора времени порядковыми номерами, у - фактические уровни ряда динамики. В качестве расчетных добавим в таблицу 3.11 гр. 3 и 4. В гр. 3 значения t возводим в квадрат (12 = 1, 22 = 4 и т.д.), в графе 4 находим произведение уt (91,581 = 91,58, 95,182 = 190,36 и т.д.). В систему нормальных уравнений подставляем данные итоговой строки, в которой предварительно произведем суммирование: 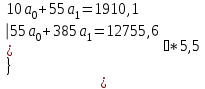 Умножим каждый член первого уравнения на 5,5, затем вычтем из второго уравнения первое: 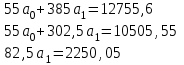 Отсюда а1 = 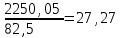 Подставим его значение в первое уравнение, чтобы рассчитать параметр ао: 10ао +5527,27 = 1910,1 10ао = 1910,1 – 1499,85 ао = 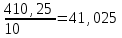 Уравнение тренда примет вид: Подставляя в него значения t для каждого года, найдем выровненные (теоретические) значения. Для 1 г. для 2 г. Занесем их в гр. 5 таблицы 3.9. При этом сумма фактических значений у и сумма выровненных Ряд выровненных значений Чтобы использовать уравнение тренда для экстраполяции временного ряда, в уравнение тренда подставляют продолженное значение времени. Например, для 11 г. t = 11 (продолжим нумерацию), тогда расчетный уровень ряда динамики, соответствующий 11 г., вычислим для 12 г.: 4) Расчет ошибки прогноза по каждой из моделей. Представим расчеты в форме табл. Значения прогнозируемого показателя, полученные по каждому из методов, возьмем из расчетов и занесем в соответствующие ячейки таблицы. Далее определим ошибку прогноза по формуле: Сравнительная таблица результатов прогнозирования
Вывод. Наиболее точные результаты прогнозирования на 2012-2013 гг. были получены с помощью трендовой модели, позволяющей получать наименьшие значения ошибки прогноза. | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||