НГ_ч2. 8. кривые линии и кривые поверхности

• Название: 8. кривые линии и кривые поверхности
• Анкор: НГ_ч2.doc
• Дата: 21.07.2018
• Размер: 3.42 Mb.
• Имя файла: НГ_ч2.doc
• Тип: Документы; #21777
• страница: 2 из 3

Рис.8.30

Пример 2 (рис.8.31). Построить линию сечения поверхности вращения фронтально проецирующей плоскостью (`).

Решение понятно из чертежа.



Рис.8.31
КОНИЧЕСКИЕ СЕЧЕНИЯ

К коническим сечениям относятся кривые линии и частные случаи таких линий, получающиеся при пересечении конуса второго порядка плоскостью. К этим линиям относятся: эллипс (в частном случае окружность), гипербола (в частном случае две пересекающиеся прямые) и парабола ( в частном случае две совпавшие прямые линии)(рис.8.32, 8.33, 8.34).

Эллипс (плоскость  пересекает все образующие конуса).

Парабола (плоскость  параллельна только одной образующей конуса).

Гипербола (плоскость  параллельна двум образующим конуса SL₁ и SL₂).



Рис.8.32 Рис.8.33



Рис.8.34

ПЕРЕСЕЧЕНИЕ ПРЯМОЙ С КРИВОЙ ПОВЕРХНОСТЬЮ

При построении точек пересечения прямой линии с кривой поверхностью вспомогательную секущую плоскость стараются выбрать таким образом, чтобы она пересекла кривую поверхность по линии, легко определяемой на чертеже, то есть по инструментально простой линии: прямой или окружности.

Алгоритм решения:

1. Заданную прямую заключают во вспомогательную секущую плоскость (чаще проецирующую);

2. Строят сечение заданной поверхности этой плоскостью;

3. Находят общие точки фигуры сечения с заданной прямой;

4. Определяют видимость прямой линии относительно поверхности. В этом случае можно воспользоваться конкурирующими точками.

Пример 1 (рис.8.35). Найти точки пересечения прямой l с поверхностью конуса.



Рис.8.35
На рис.8.35 вспомогательная секущая плоскость проведена через прямую l и вершину S конуса. Она пересекла конус по образующим SL₁ и SL₂.

Вспомогательная секущая плоскость задана прямыми S1 и S2, а ее горизонтальный след - линия АВ.



Рис.8.36
Задачи на взаимное пересечение прямой линии с кривой поверхностью - задачи третьего типа могут быть сведены к задачам второго типа путем преобразования комплексного чертежа.

Пример 1 (рис.8.37). Найти точки M и N пересечения прямой l с цилиндрической поверхностью вращения.

Решение:

Преобразуем заменой плоскостей проекций чертеж так, чтобы цилиндрическая поверхность стала проецирующей.

Одновременно с этим прямая l (1,2) преобразуется в линию l^IV(1^IV,2^IV), точки пересечения которой с очерком цилиндрической поверхности - M^IV и N^IV и будут искомыми.

Обратным преобразованием найдем эти точки на исходных проекциях

Построения ясны из чертежа.



Рис.8.37

9. ВЗАИМНОЕ ПЕРЕСЕЧЕНИЕ КРИВЫХ ПОВЕРХНОСТЕЙ

Для построения линий взаимного пересечения двух кривых поверхностей пользуются методом вспомогательных секущих поверхностей. В качестве которых используются не только вспомогательные секущие плоскости, но и вспомогательные секущие поверхности: цилиндрические, конические и сферы, выбор которых в качестве “посредников” позволяет находить точки искомой линии пересечения.

1. Возможности применения способа вспомогательных секущих плоскостей в качестве “посредников”.

Вспомогательные секущие плоскости применимы, если заданы:

- две поверхности вращения, оси которых перпендикулярны к одной из плоскостей проекций;

- два цилиндра или два конуса, или конус и цилиндр;

- две линейчатые поверхности с общей плоскостью параллелизма;

- две каркасные поверхности.

Пример 1(рис.9.1). Построить линию пересечения сферы с конусом.

Решение:

1. Находим характерные и опорные точки искомой линии пересечения.

Такими точками будут точки пересечения очерковых образующих: А, В, С и С₁. Точки С и С₁ получены с помощью вспомогательной секущей плоскости , проходящей через экватор сферы.

2. Промежуточные точки искомой линии находим с помощью семейства вспомогательных секущих плоскостей: ₁, ₂,...

3. Соединяя последовательно найденные точки А, М, С, N,..В получаем проекции искомой линии.

4. Определяем видимость.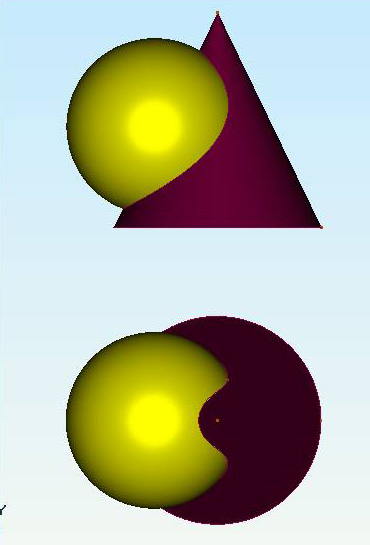



Рис.9.1
Пример 2 (рис.9.2). Построить линию взаимного пересечения поверхностей цилиндра и тора.

Решение:

Обе заданные поверхности имеют общую плоскость симметрии, параллельную фронтальной плоскости проекций и потому точки искомой линии пересечения можно найти с помощью вспомогательных секущих плоскостей: , ₁, ₂,...

Построение начинаем с опорных точек А и В искомой линии, принадлежащих очерковым образующим.



Рис.9.2
2. Возможности применения вспомогательных секущих сфер в качестве “посредников”.

Применение вспомогательных секущих сфер возможно в следующих случаях, когда на чертеже заданы:

1. Две поверхности вращения, оси которых пересекаются и параллельны одной из плоскостей проекций;

2. Две поверхности вращения, оси которых пересекаются, но ось одной из них параллельны, а ось другой - перпендикулярна к одной и той же плоскости проекций.

3. Когда на чертеже заданы две поверхности с общей плоскостью симметрии и одна из них является поверхностью вращения, а другая поверхность имеет семейство плоских круговых сечений, перпендикулярных общей плоскости симметрии.

Рассмотрим эти случаи на примерах.

Если на чертеже заданы две поверхности вращения, оси которых пересекаются и параллельны плоскости чертежа, то точки искомой линии пересечения могут быть найдены с помощью вспомогательных секущих концентрических сфер с центром в точке пересечения осей.

Пример 1 (рис.9.3). Построить линию пересечения поверхности конуса вращения с тором.

Решение:

Из точки О пересечения осей опишем некоторую сферу радиуса R. Она пересечет конус по двум параллелям: 1-1 и 2-2, а тор - по 3-3. Общие точки Е и Е пересечения параллелей 1-1 и 3-3 будут точками искомой линии пересечения заданных поверхностей.

По аналогии, описывая новые сферы, получим необходимое и достаточное количество точек искомой линии пересечения.

Примечание.

Сфера минимального радиуса R₁ будет касаться одной из поверхностей вращения и пересекать другую. В данном случае, она касается конуса и пересекает тор по параллели 4-4.

Точки С и С₁ получены с помощью вспомогательной горизонтальной плоскости , проведенной через ось тора.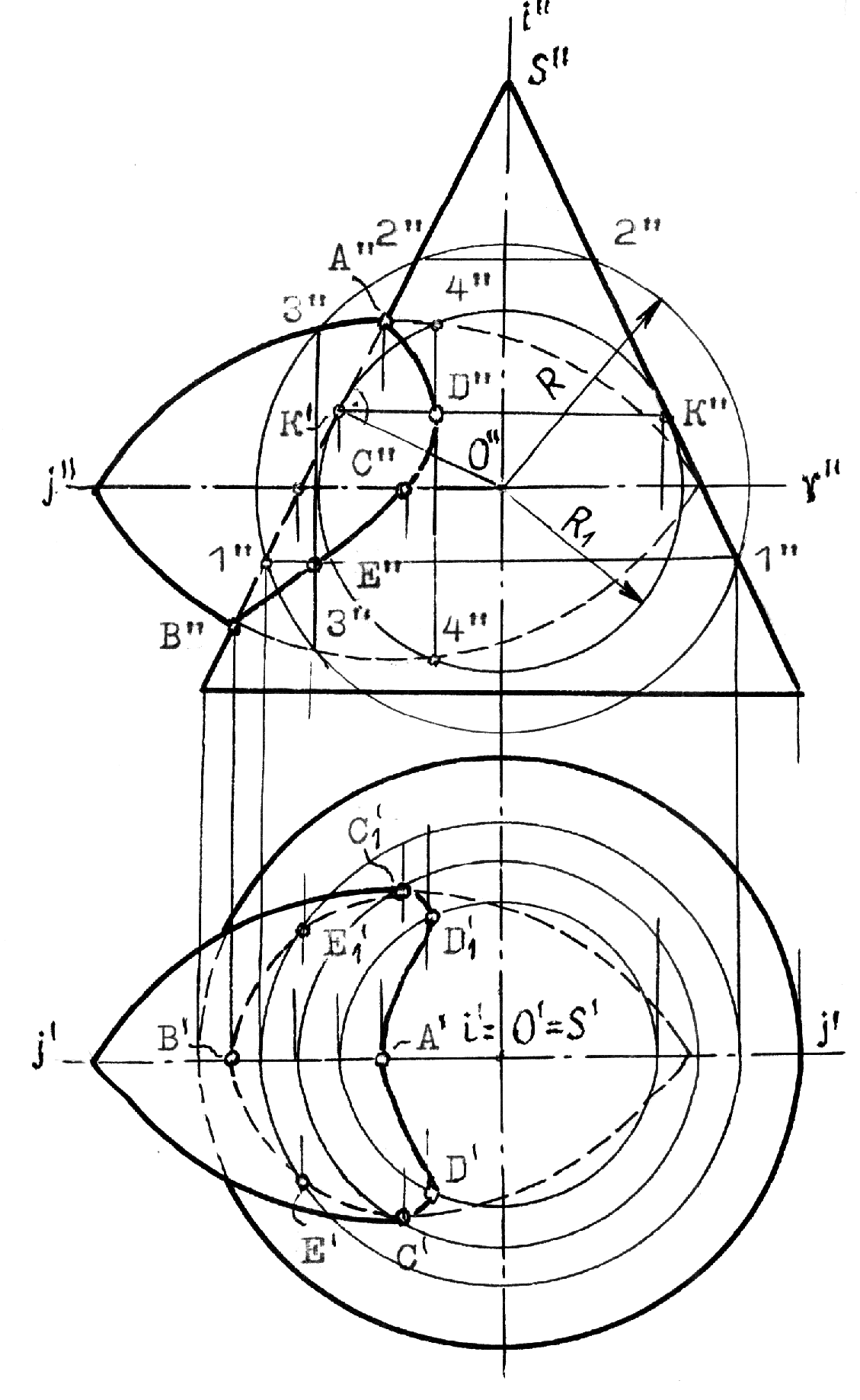




Рис.9.3
Идея применения способа вспомогательных секущих сфер основана на свойстве взаимного пересечения двух соосных поверхностей вращения, то есть имеющих общую ось вращения, по общим для них параллелям (рис.9.4).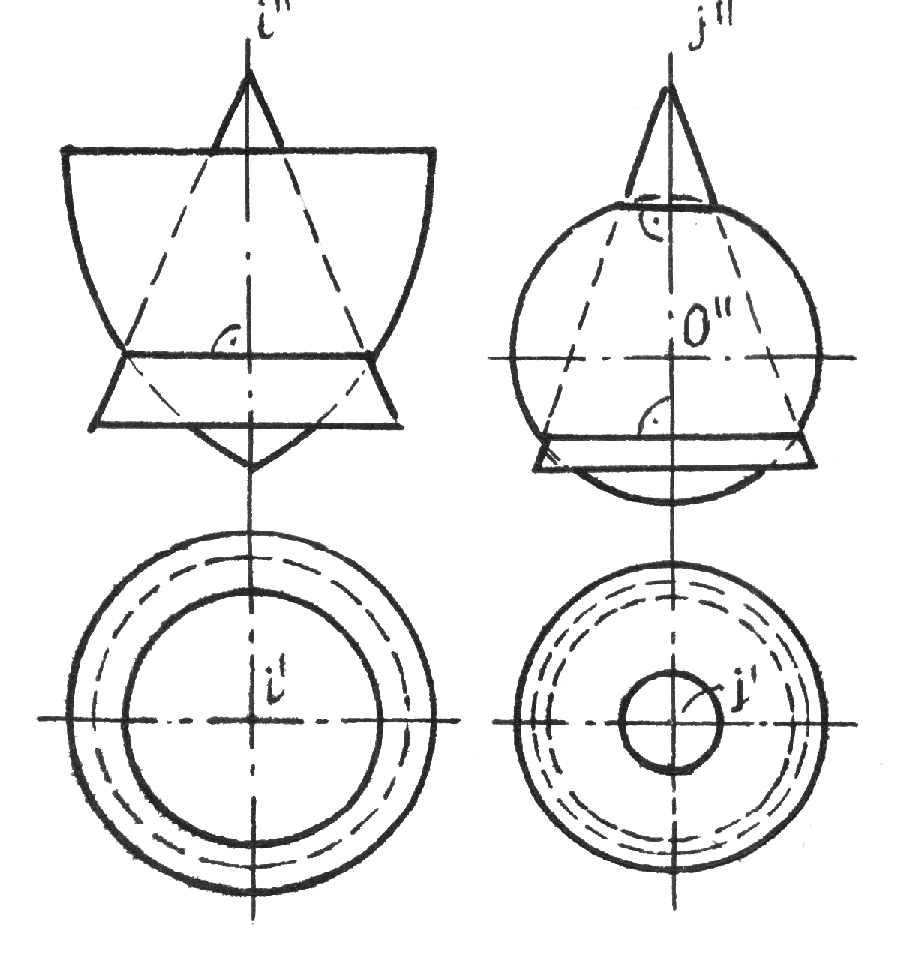



Рис.9.4
Пример 2 (рис.9.5). Построить линию взаимного пересечения поверхностей конуса и тора.

Решение:

В данном случае ось конуса параллельна, а ось тора - перпендикулярна горизонтальной плоскости проекций. Поэтому очерки вспомогательной секущей сферы некоторого радиуса Р нужно провести из точки О пересечения осей заданных поверхностей на той и другой плоскостях проекций. При этом на фронтальной проекции фигур сфера пересечет тор по параллели 1-1, а на горизонтальной плоскости проекций эта же сфера пересечет конус по параллелям 2-2 и 3-3. Поскольку окружность 1-1 проецируется на горизонтальную плоскость проекций в истинную величину, а параллели конуса - в прямые линии, то точки М и М пересечения этих линий и будут искомыми точками линии пересечения.

Аналогично можно найти необходимое и достаточное количество точек для построения проекций линии пересечения поверхностей.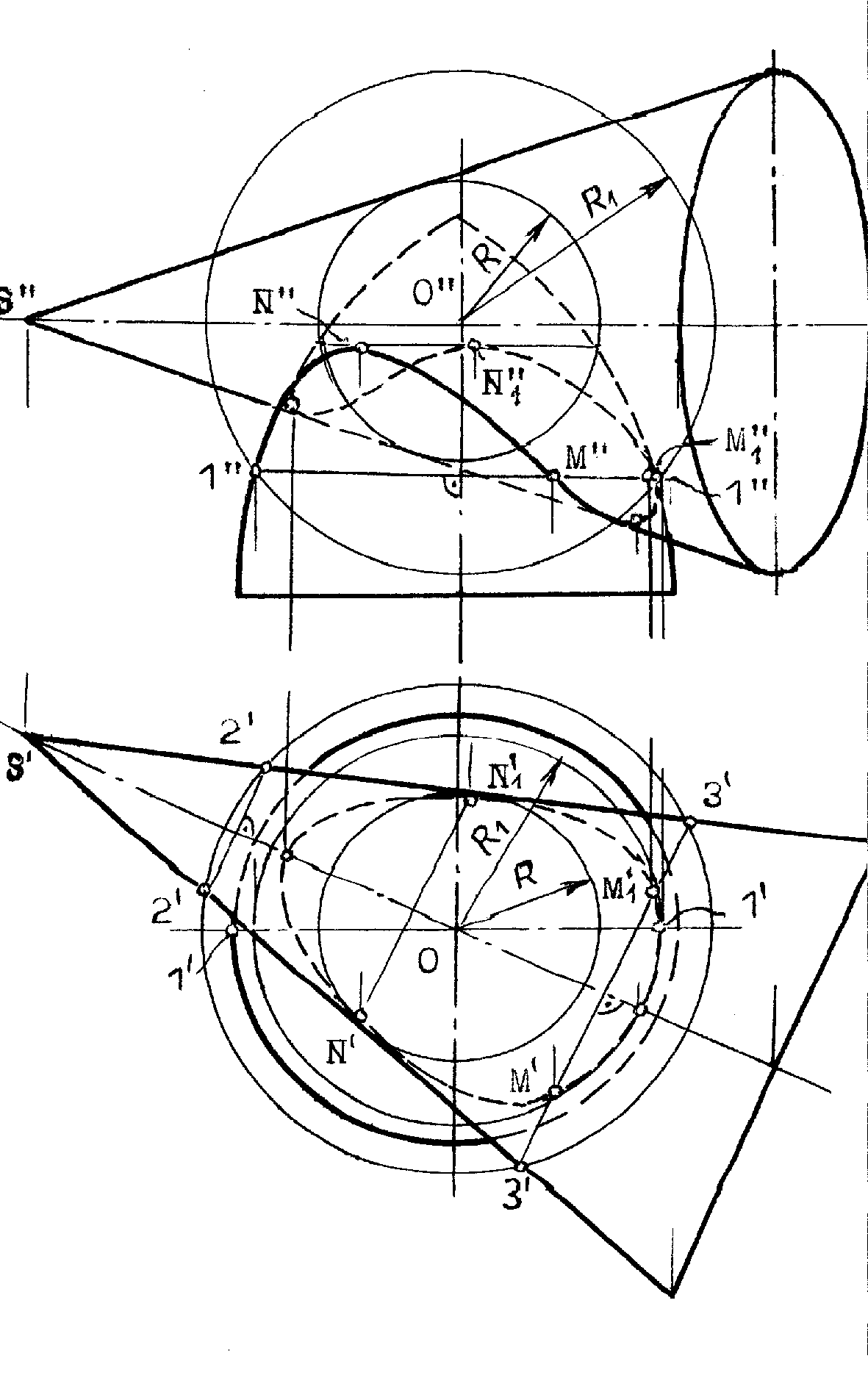



Рис.9.5
Пример 3 (рис.9.6). Построить линию взаимного пересечения поверхностей двух торов.

Решение: Обе заданные поверхности имеют общую плоскость симметрии, параллельную фронтальной плоскости проекций. Причем открытый (тор-кольцо) имеет семейство круговых сечений, перпендикулярных плоскости симметрии. Это третий из рассматриваемых случаев, когда невозможно применение вспомогательных секущих сфер в качестве “посредников”.

Нахождение точек искомой линии пересечения заданных поверхностей начинаем с определения опорных точек А и В, в интервале между которыми расположится искомая линия пересечения поверхностей.

Выбираем на поверхности тора-кольца произвольное круговое сечение 1-1, лежащее в плоскости, проходящей через ось j вращения тора-кольца. Из центра С₁ восставим перпендикуляр к линии 1-1, который пересечет ось второго тора в точке О₁.

Из точки О₁ опишем сферу радиуса О₁-1, пересекающую второй тор по окружности 2-2.

Общие точки М и М₁ окружностей 1-1 и 2-2 и будут точками искомой линии пересечения заданных поверхностей.

Таким же способом найдены точки N и N₁ и другие не указанные точки.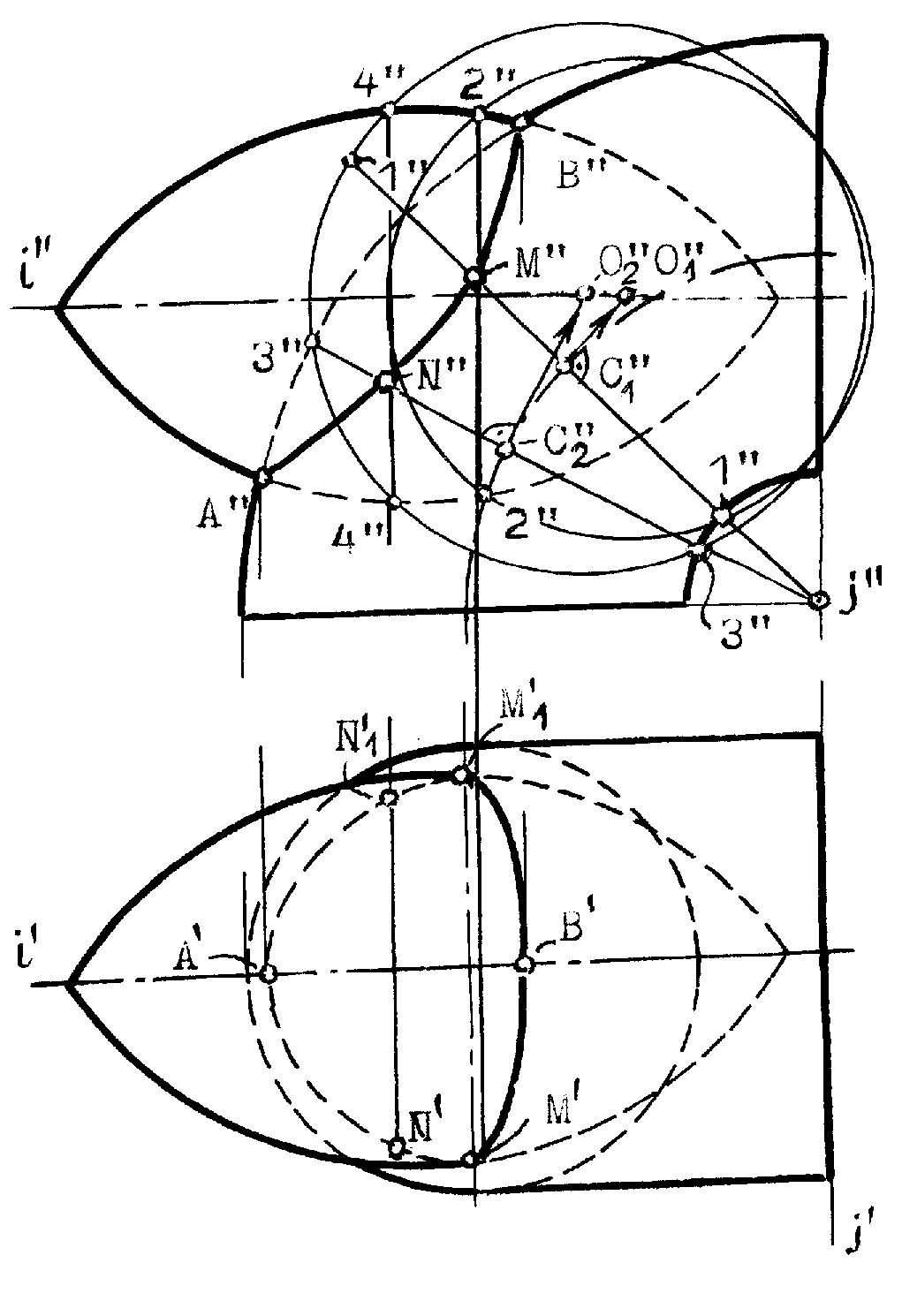



Рис.9.6
ВЗАИМНОЕ ПЕРЕСЕЧЕНИЕ ПОВЕРХНОСТЕЙ ВТОРОГО ПОРЯДКА

Две поверхности второго порядка пересекаются по кривой четвертого порядка.

На общую плоскость симметрии поверхностей кривая их пересечения проецируется кривой второго порядка.

Если часть кривой пересечения двух поверхностей второго порядка есть кривая второго порядка, то другая часть - также линия второго порядка ( в том числе могут быть и пары прямых).

Две линии второго порядка, лежащие на одной поверхности второго порядка, можно провести другую поверхность второго порядка
Теорема Монжа: две поверхности второго порядка, описанные вокруг третьей поверхности второго порядка или вписанные в нее, пересекаются между собой по двум кривым второго порядка.

Значит, в этом случае пространственная кривая распадается на пару плоских кривых (рис.9.7).

Если две поверхности второго порядка имеют две общие соприкасающиеся с ними плоскости, то линия их пересечения распадается на пару кривых второго порядка (рис.9.8).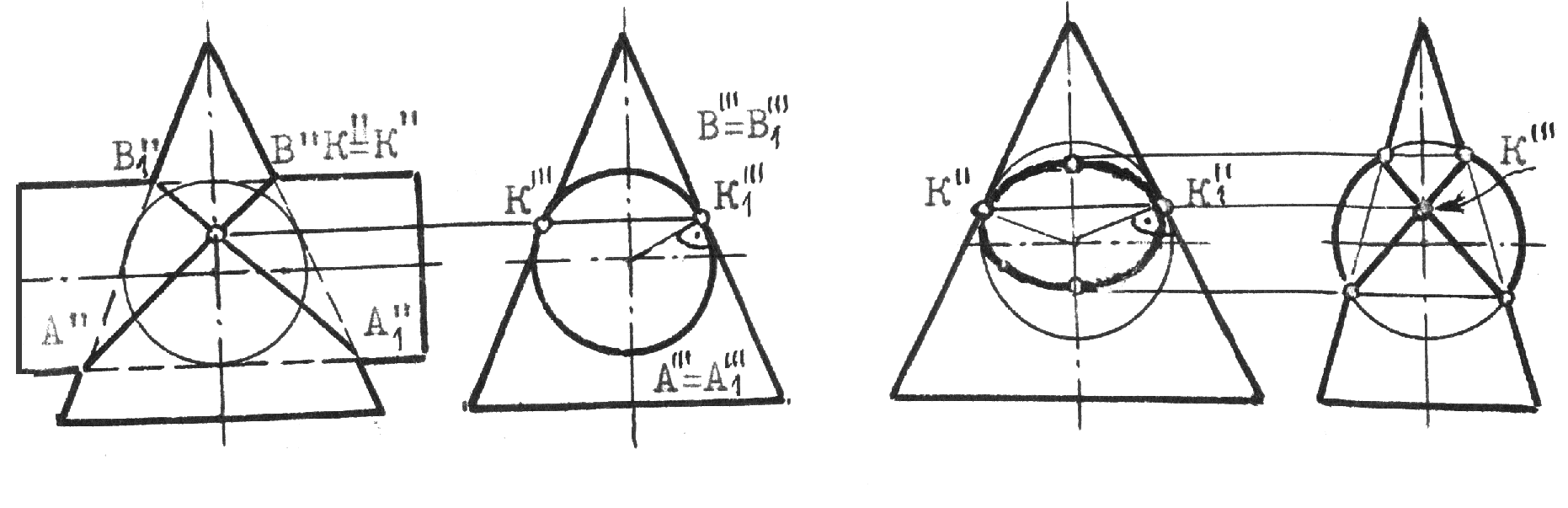



Рис.9.7 Рис.9.8
Проекция сечения эллипсоида вращения на плоскости, перпендикулярной к его оси, является эллипс, большая ось которого перпендикулярна к плоскости общей симметрии (рис.9.9).

Проекция эллиптического сечения однополостного гиперболоида вращения на плоскости, перпендикулярной к его оси, является эллипс, малая ось которого перпендикулярна общей плоскости симметрии поверхности (рис.9.10).

Проекция эллиптического сечения параболоида вращения на плоскости, перпендикулярной к его оси вращения, есть окружность (рис.9.11).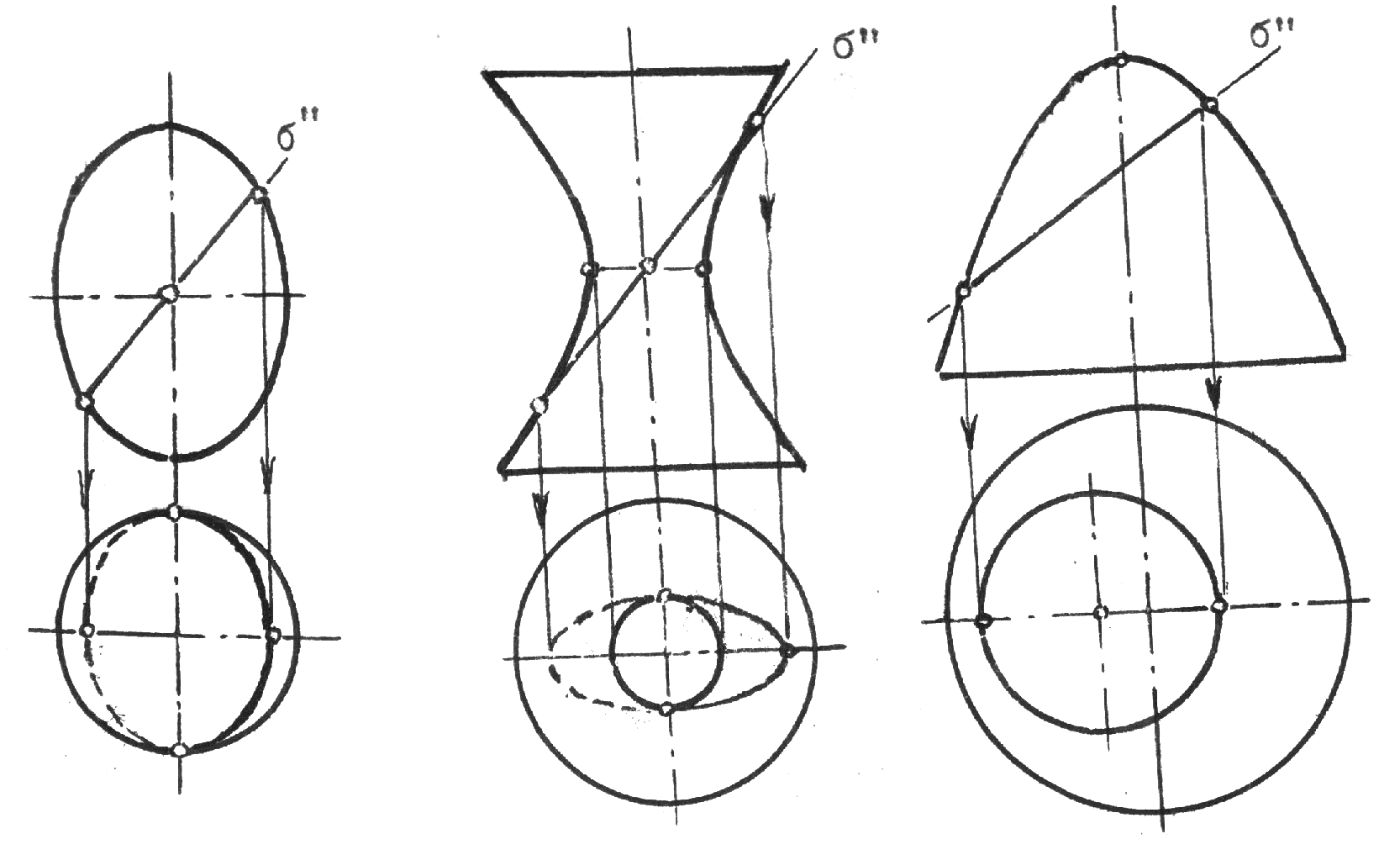



Рис.9.9 Рис.9.10 Рис.9.11
РАЗВЕРТКИ КРИВЫХ ПОВЕРХНОСТЕЙ

Кривые поверхности, которые полностью, без растяжения или сжатия, без разрывов и складок можно совместить с плоскостью, называют развертываемыми. К этим поверхностям относятся лишь линейчатые и только такие, у которых смежные образующие пересекаются между собой или параллельны. Этим свойством обладают торсы (поверхности, образованные прямыми, касательными к направляющей пространственной кривой)., конические и цилиндрические поверхности.

Остальные линейчатые поверхности, а также все нелинейчатые - являются неразвертываемыми.
Построение полной развертки прямого кругового усеченного цилиндра вращения (рис.9.12).

Для построения развертки цилиндра достаточно представить его как призму с большим количеством граней (фактически достаточно 12-16 таких граней), равномерно разделив окружность основания цилиндра на равное число частей.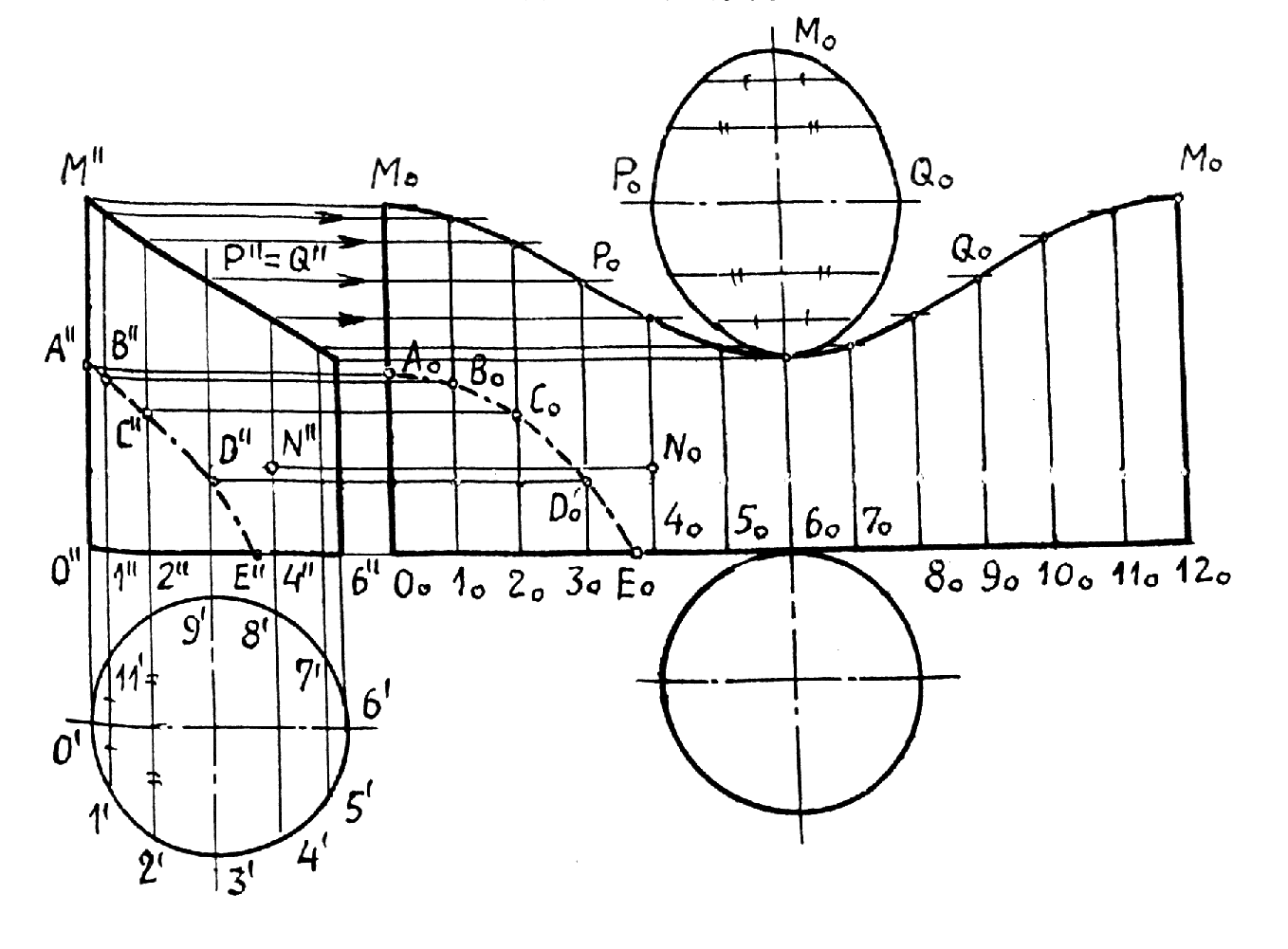


Рис.9.12
Если на поверхности цилиндра расположена какая-либо линия, то на развертку цилиндра эту линию можно перенести по точкам, принадлежащим соответствующим образующим этой поверхности.
Построения развертки полной поверхности прямого

кругового конуса (рис.9.13).

Для построения развертки прямого кругового конуса достаточно представить его поверхность как правильную пирамиду с большим числом граней и далее построить ее развертку, найдя натуральную величину одной из граней, представляющей собой равнобедренный треугольник, по его боковой стороне и основанию. Построение развертки конуса видно из чертежа, где основание “грани” S01 равно хорде 0<sup>`</sup>1`. Развертка боковой поверхности конуса, в данном случае, содержит 12 таких “граней”.

Развертка боковой поверхности будет найдена точнее, если определить угол ⁰ при точке S на развертке по формуле:

⁰=R/l 360⁰, где R - радиус основания конуса, а l - длина образующей конуса.



Рис.9.13
Принадлежащие боковой поверхности конуса точки некоторой кривой АВСDЕ можно найти по принадлежности этих точек соответствующим образующим конической поверхности. Для этого достаточно способом вращения, как показано на примере точки С, принадлежащей образующей S2, найти отрезки S``B``₀=SB, S``D``₀=SD и S``E``₀=SE ... Найденные отрезки отложить по соответствующим образующим на развертке конуса и провести через них линию АВСDE.

Для получения полной развертки поверхности конуса ее нужно дополнить основанием конуса, касательным в соответствующей точке развертки боковой поверхности.

Развертка боковой поверхности наклонного конуса находиться как развертка наклонной пирамиды с большим количеством граней, каждую из которых находят по трем сторонам - двум боковым “ребрам” и “основанию”.(рис.9.14).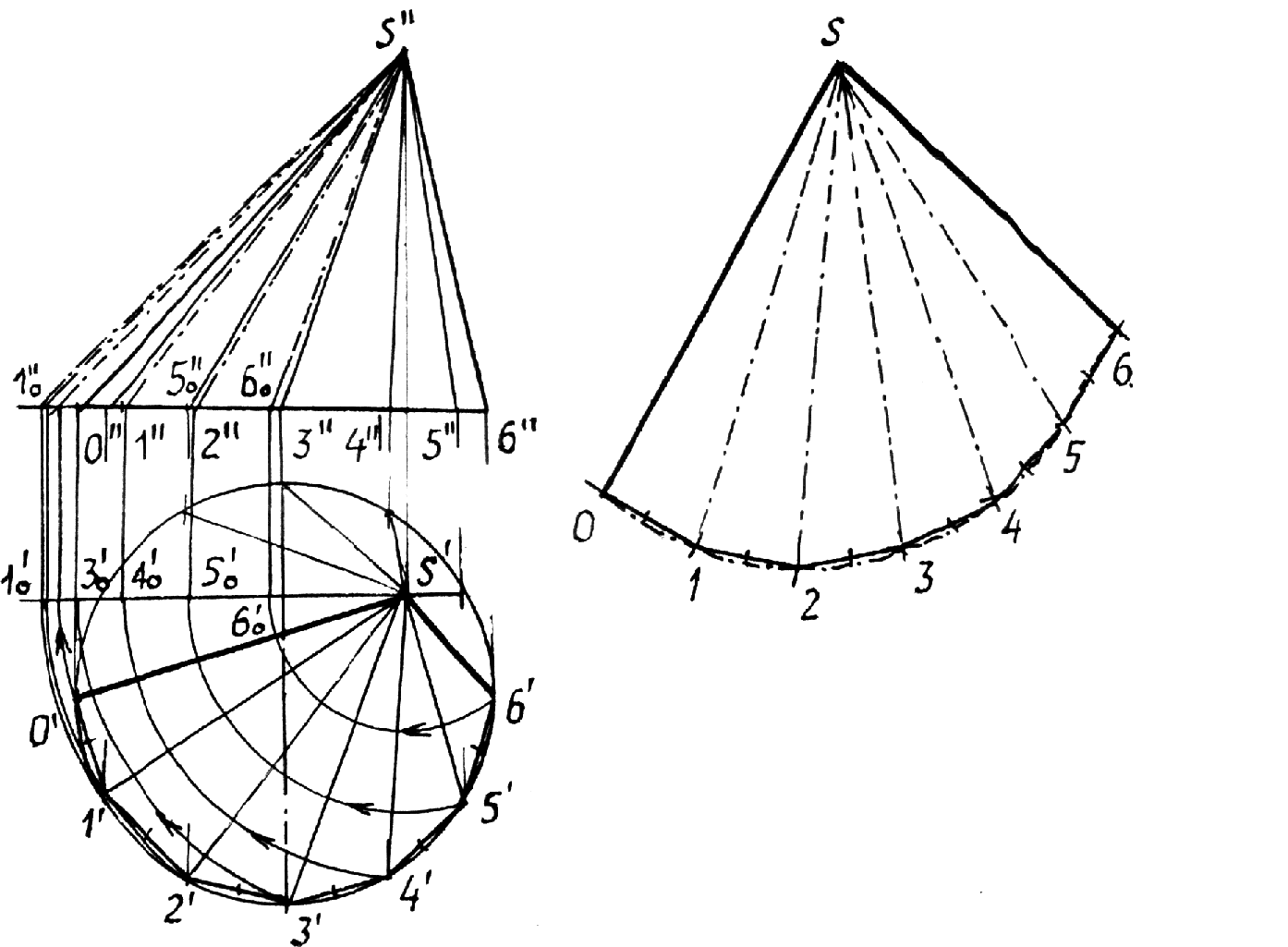



Отсек поверхности наклонного кругового конуса и его развертка.

Рис.9.14
При построении развертки необходимо обратить внимание на то, чтобы внешняя поверхность конуса на развертке была обращена наружу, к наблюдателю, как указано на рис.9.12 - 9.14.
10. АКСОНОМЕТРИЧЕСКИЕ ПРОЕКЦИИ

1.Общие замечания.

При построении комплексного чертежа предмета последний обычно располагают так, чтобы направления трех главных измерений его были параллельны плоскостям проекций: направление длины - параллельно оси х, ширины - оси y и высоты - оси z.

Тогда длина и высота проецируются в натуральную величину на фронтальную плоскость проекций, длина и ширина не искажаются на горизонтальной проекции, а ширина и высота - на профильной.

Такой чертеж нетрудно строить, по нему просто производить измерения, судить о размерах изображаемого предмета. Однако, он недостаточно нагляден. На каждой из проекций отсутствует одно из трех измерений. Чтобы воспроизвести форму предмета, надо мысленно воссоздать ее по двум, трем, а иногда и большему числу проекций.

Более наглядный чертеж можно получить, проецируя предмет на одну плоскость проекций и располагая его так, чтобы ни одно из направлений главных измерений не проецировалось точкой.

2. Чтобы образовать аксонометрический чертеж некоторой фигуры, например, точки А, необходимо жестко связать эту фигуру с некоторой декартовой системой координат 0хyz. При этом на координатных осях: 0х, 0y, и 0z зададим единую определенную натуральную единицу измерения е (в мм, см и тому подобное).

Так как точка А жестко связана с натуральной системой координат, то можно построить ее проекции на любую координатную плоскость. Например, построить проекцию А` точки А на плоскость <sub>1</sub>(0хy). После этого точку А и ее проекцию А` и натуральные координатные оси параллельно проецируем на плоскость аксонометрического чертежа ₀ по направлению s (рис.10.1).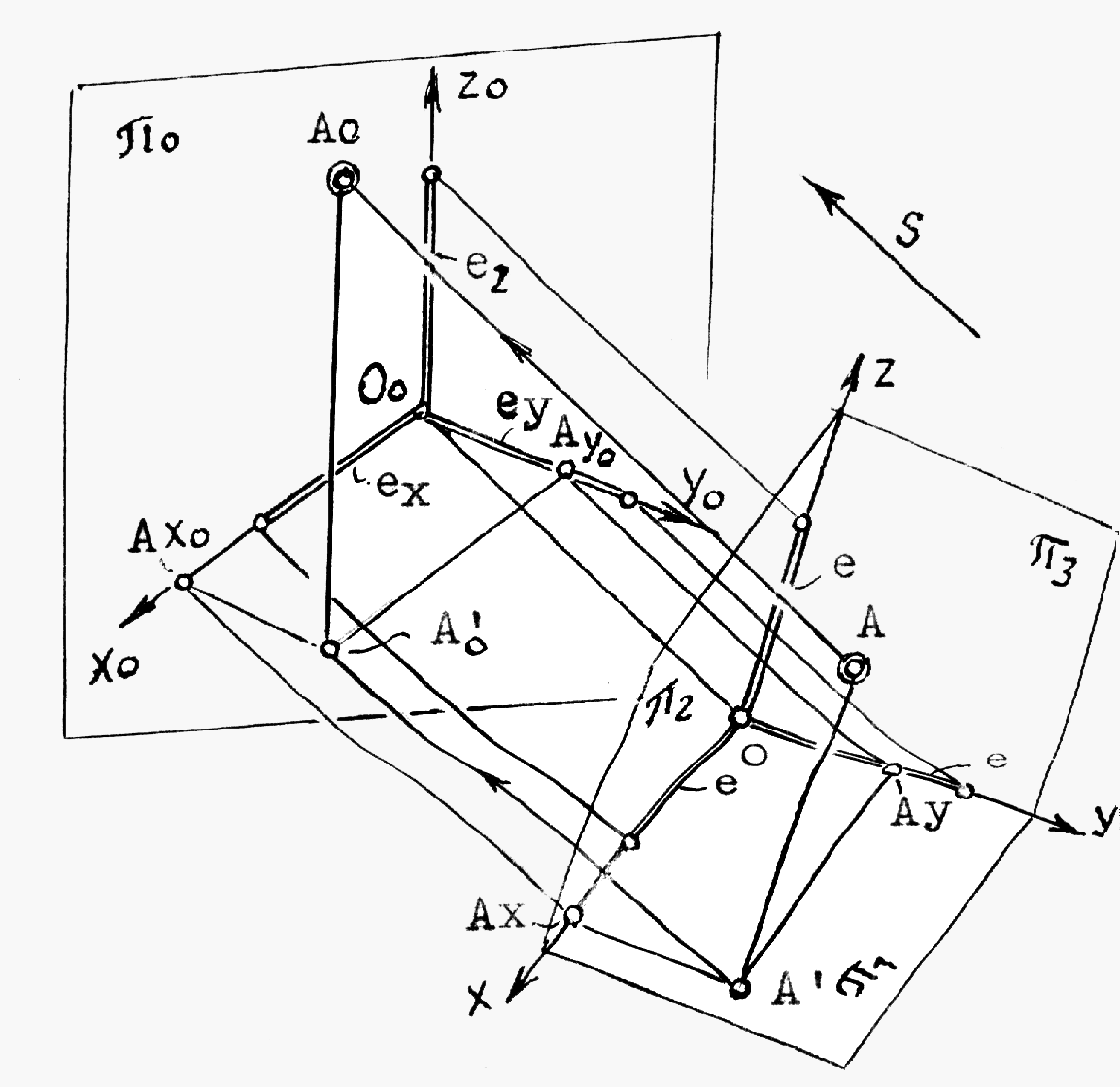


Рис.10.1

Полученную совокупность проекций (А₀, А`₀, х₀, y₀ и z₀) на ₀ будем называть аксонометрическим чертежом заданной фигуры - точки А,

Прямые х₀, y₀ и z₀ называются аксонометрическими осями.

Проекция А₀ называется главной аксонометрической проекцией точки А, а проекции А`₀ - вторичной. Очевидно, на полученном чертеже могут быть построены и другие вторичные проекции точки А: А``₀ и A```₀.

3. Отношение длины аксонометрического координатного отрезка 0₀Ах₀ к длине натурального координатного отрезка 0Ах называется показателем искажения по оси 0₀х₀ и обозначается буквой u: u=0₀Ax₀: 0Ах. Иначе, е_х: е=u.

Такой же смысл имеют показатели искажения e_y и e_z:

v=0₀Ay₀: и w=0₀Ax₀:0A_z.

Показатели искажения по осям в общем случае различны:

uvwu. В частном случае, когда u=v=w акснометрический чертеж называют изометрическим чертежом или короче - изометрией.

Если показатели искажения по двум осям равны между собой, а по третьей оси показатель искажения отличается от первых двух (u=wv и т.п.), то чертеж называется диметрическим, или кратко, - диметрией.

В общем случае, когда uvw, то такой чертеж называют триметрией.

4.Основная теорема аксонометрии - торема Польке (1851), утверждает:

Любые три отрезка на плоскости, исходящие из одной точки, могут быть приняты за параллельную проекцию трех равных и взаимно перпендикулярных пространственных отрезков.

В зависимости от направления параллельного проецирования по отношению к плоскости аксонометрического изображения различают косоугольные и прямоугольные аксонометрические проекции.

Между показателями искажения и углом наклона проецирования по отношению к плоскости аксонометрического изображения существует зависимость: u²+v²+w²=2+ctg².

Для прямоугольной аксонометрической проекции угол =90⁰, следовательно: u²+v²+w²=2. Где:

12+v²<2 и

12+w²<2.

Теорема Вейсхбаха (1840):

Оси прямоугольной аксонометрической проекции являются биссектрисами углов треугольника, стороны которого пропорциональны квадратам коэффициентов искажения.

Таким образом, зная коэффициенты искажения некоторой прямоугольной аксонометрической проекции, можно найти ее аксонометрические оси (рис.10.2)