НГ_ч2. 8. кривые линии и кривые поверхности
 Скачать 3.42 Mb. Скачать 3.42 Mb.
|
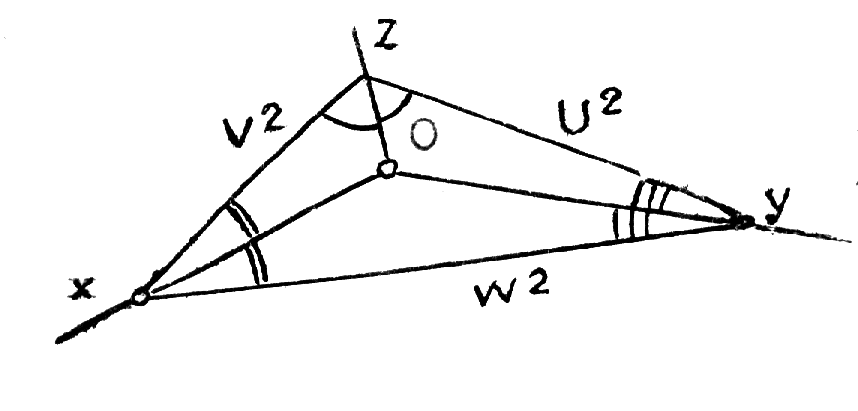 Рис.10.2 5.Построение осей и коэффициентов искажения прямоугольной аксонометрической проекции по треугольнику следов. Если плоскость аксонометрической проекции пересекает плоскости пространственной системы координат, то фигурой сечения будет остроугольный треугольник XYZ - треугольник следов: XY, XZ и YZ. Оси пространственной системы координат спроецируются на плоскость аксонометрического изображения - высотами этого треугольника (совпадут с направлениями высот данного треугольника)(рис.10.3) и (рис.10.4). 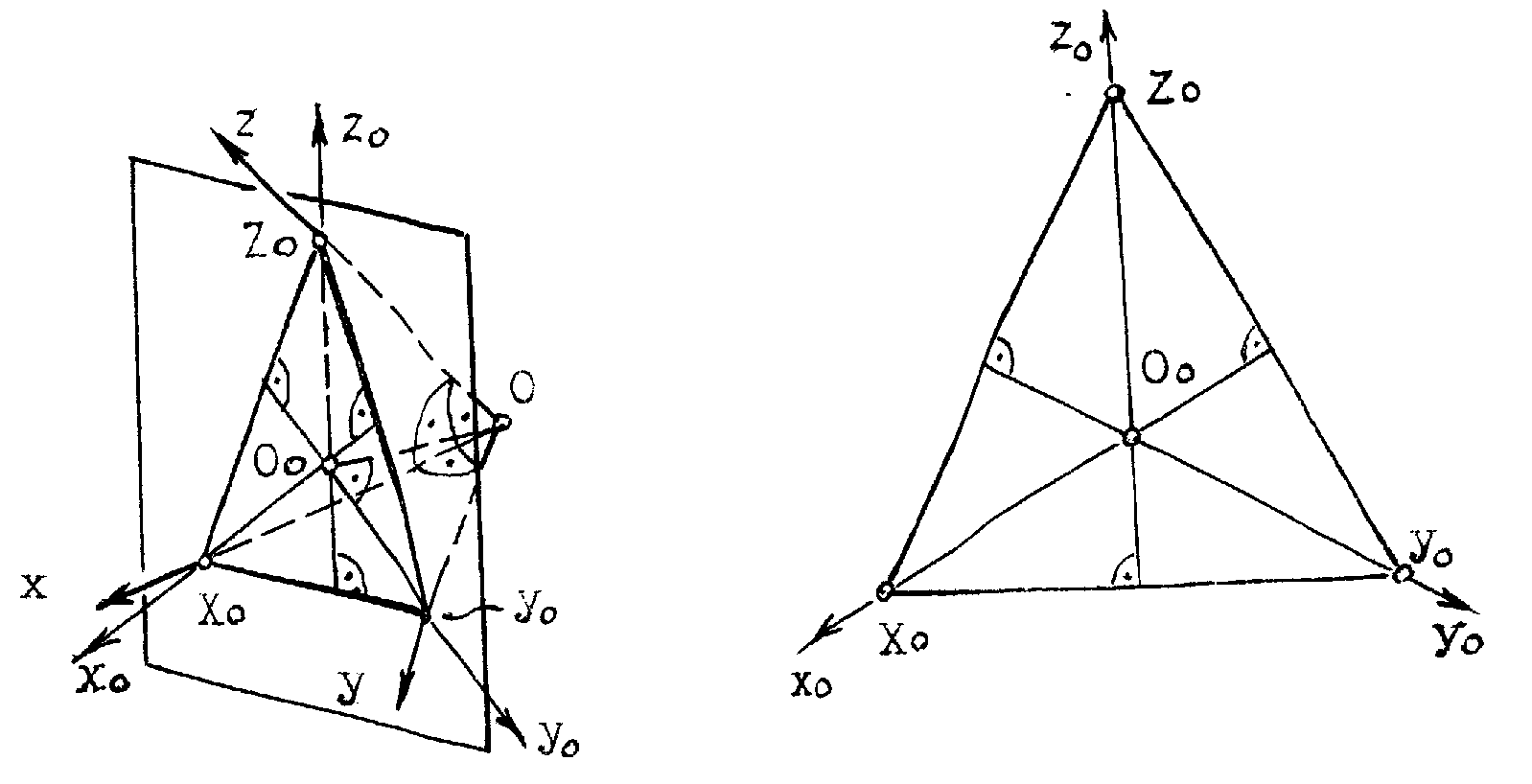 Рис.10.3 Рис.10.4 Если задано направление аксонометрических осей Ox, Оy и Оz, то, построив произвольный треугольник следов, можно найти величины коэффициентов искажения по этим осям, задавшись величиной единичного отрезка е (рис.10.5). Решение: 1.Строим треугольник следов (произвольный); 2. Находим совмещенное положение треугольников XOY и XOZ с плоскостью аксонометрического изображения. Получаем XOY и ZOY. 3. Отложив на направлении OX, OY и OZ отрезки равные e (единичный масштаб), находим его проекции: ех, еy и еz на аксонометрических осях. 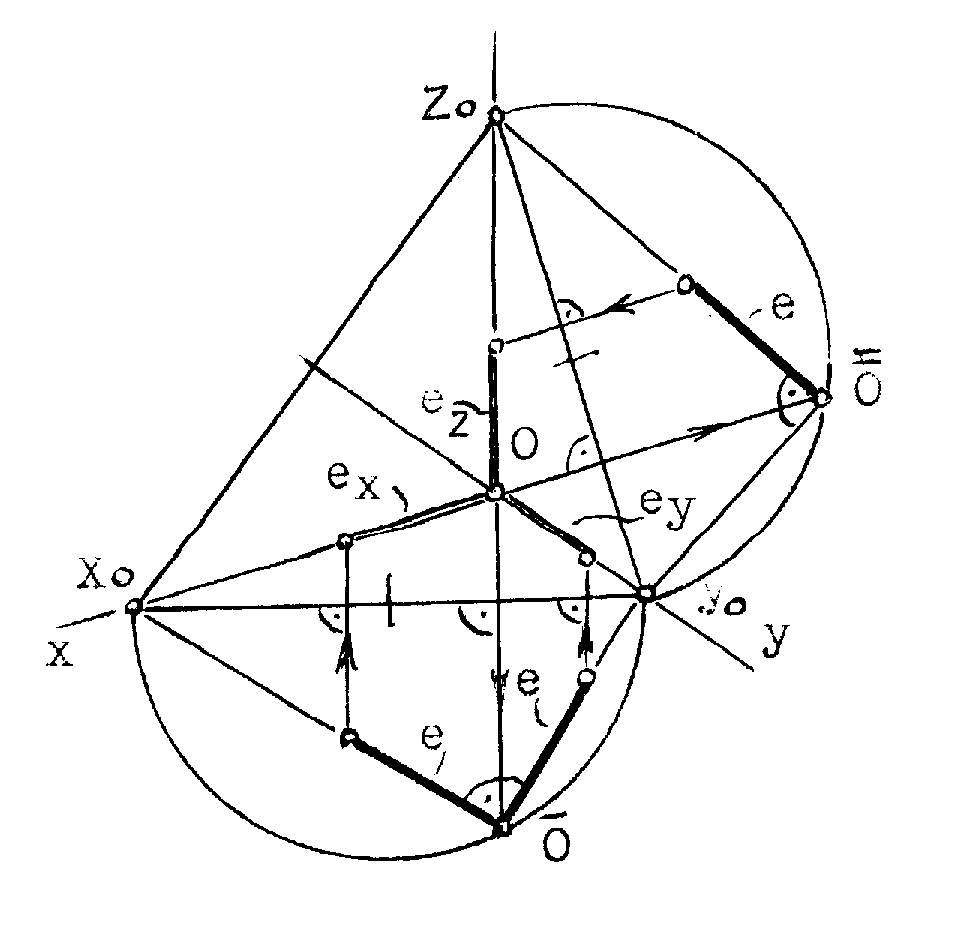 Рис.10.5 ТЕОРЕМЫ ОРТОГОНАЛЬНОЙ АКСОНОМЕТРИИ Теорема. Аксонометрические оси ортогональной аксонометрии являются высотами треугольника следов Теорема. Треугольник следов на прямоугольном трехграннике координат всегда остроуголен Теорема. В ортогональном аксонометрии сумма квадратов показателей искажений всегда равна двум Теорема Вейсбаха. Если стороны треугольника пропорциональны квадратам показателей искажения, то его биссектрисы могут быть приняты за аксонометрические оси. Обратная теорема: Если биссектрисы какого-либо треугольника являются аксонометрическими осями, тогда этот треугольник есть треугольник искажений. Теорема Любой треугольник является треугольником искажений для некоторой прямоугольной аксонометрической системы. Теорема. Сторону любого остроугольного треугольника можно принять за аксонометрические масштабы некоторой прямоугольной аксонометрической системы. СТАНДАРТНЫЕ АКСОНОМЕТРИЧЕСКИЕ ПРОЕКЦИИ ГОСТ 2.317-69 устанавливает аксонометрические проекции, применяемые в чертежах всех отраслей промышленности и строительства. Рассмотрим из них прямоугольную изометрическую и прямоугольную диметрическую проекции. Прямоугольная изометрическая проекция. Положение осей и их построение видно из рис. 10.6 и 10.7. Коэффициенты искажения по всем трем осям равны 0,82. При этом масштаб изображения будет натуральным, то есть М 1:1. 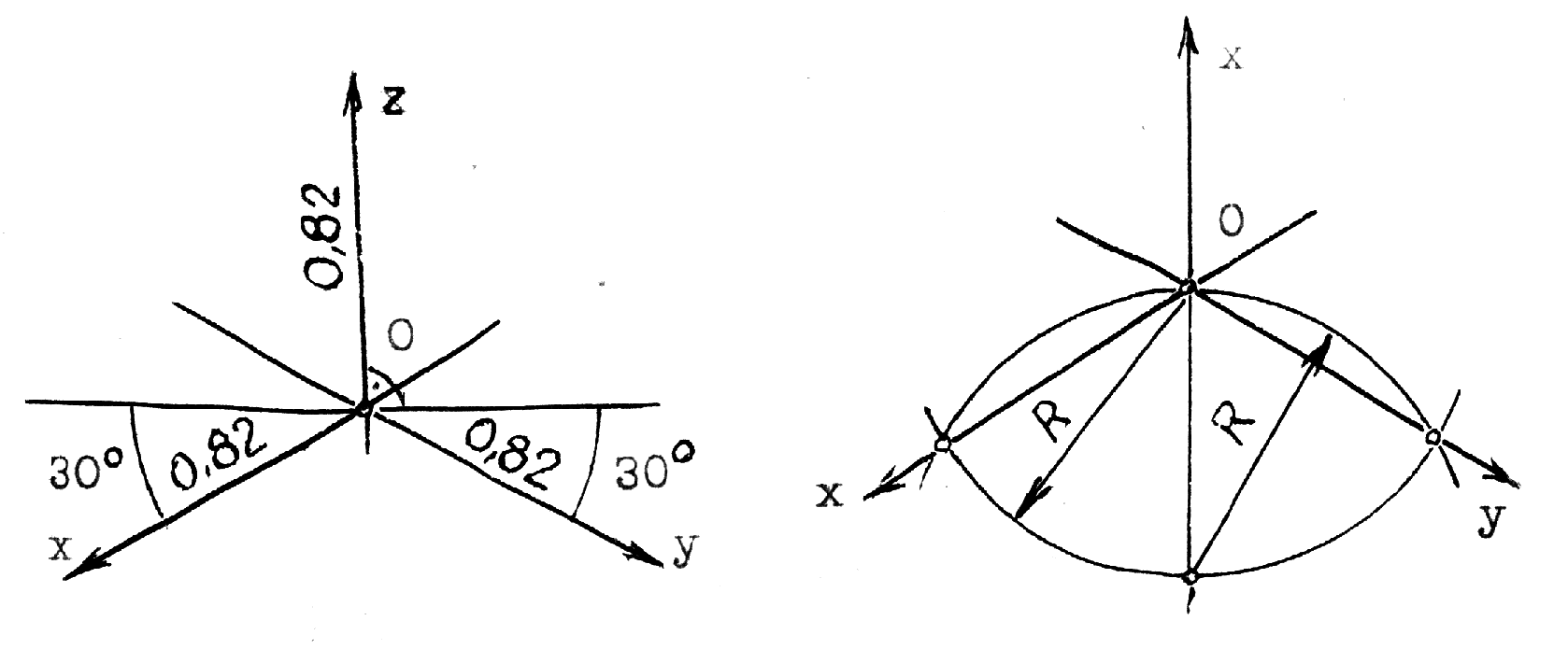 Рис.10.6 Рис.10.7 При выполнении изометрии возможно округление коэффициентов искажения до 1. Тогда масштаб изображения будет М 1,22 :1. Прямоугольная диметрическая проекция Положение осей и их построение видно из рис.10.8 и 10.9. Коэффициенты искажения по осям 0х и 0y будут 0,94, а по оси 0y - 0,47. При этом масштаб изображения будет М 1:1. При округлении коэффициентов искажения соответственно до 1 и 0,5 масштаб изображения диметрической проекции будет М 1,06:1. 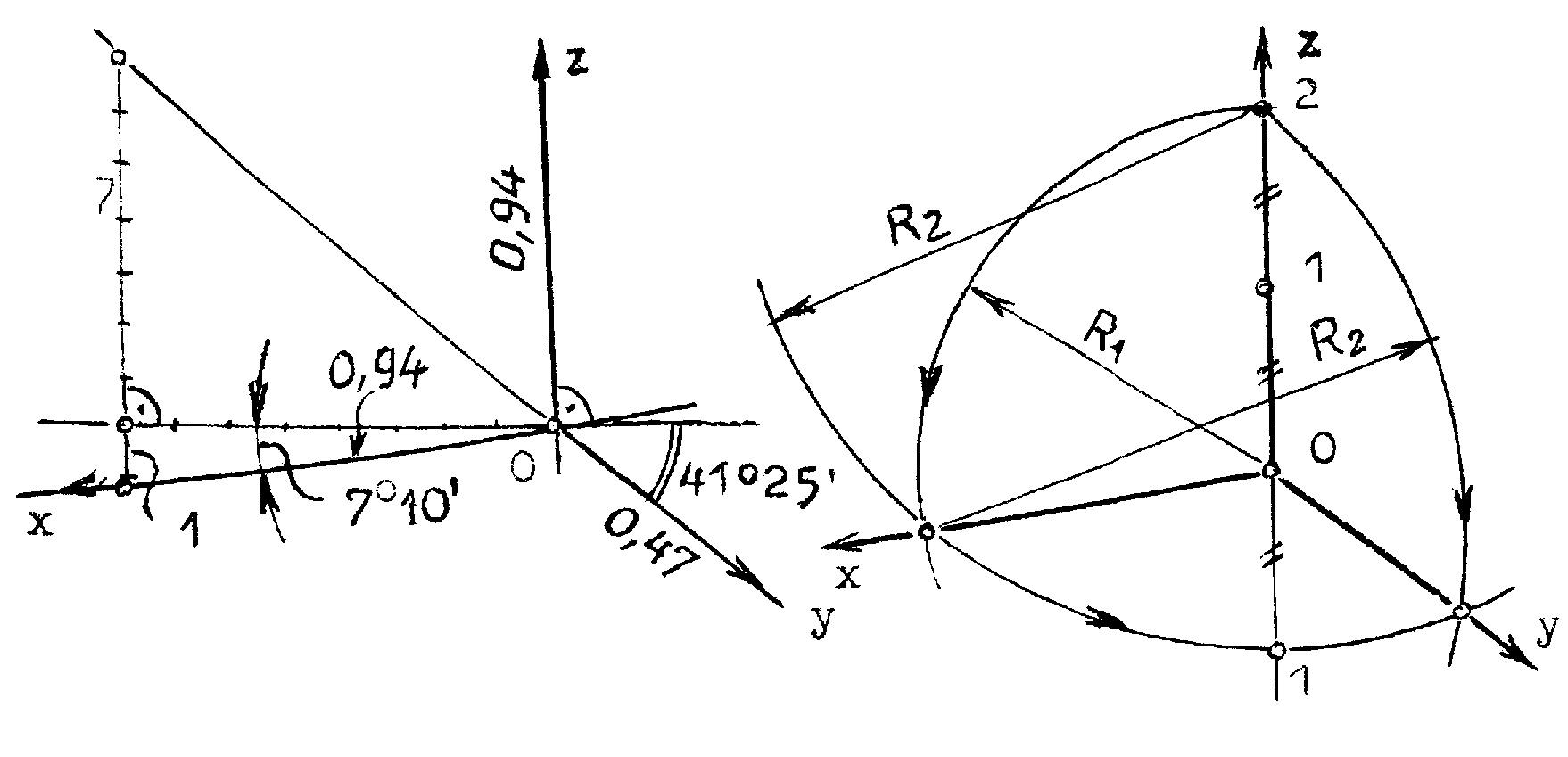 Рис.10.8 Рис.10.9 ИЗОБРАЖЕНИЕ ОКРУЖНОСТИ В КООРДИНАТНОЙ ПЛОСКОСТИ ИЗОМЕТРИЧЕСКОЙ ПРОЕКЦИИ Пример 1 (рис. 10.10, 10.11), построить окружность диаметром 50 мм в плоскости 0ху. Решение: Проведем в плоскости окружности несколько хорд, параллельных оси 0х, которые пересекут ее очерк в точках:1, 2, 3 ... Используя систему координатных осей 00х0у0 изометрической проекции, найдем изображения этих точек в изометрии. Для этой цели используем приведенную изометрическую проекцию, при построении которой коэффициенты искажения округляются до 1. При этом масштаб изображения будет М 1,22:1. 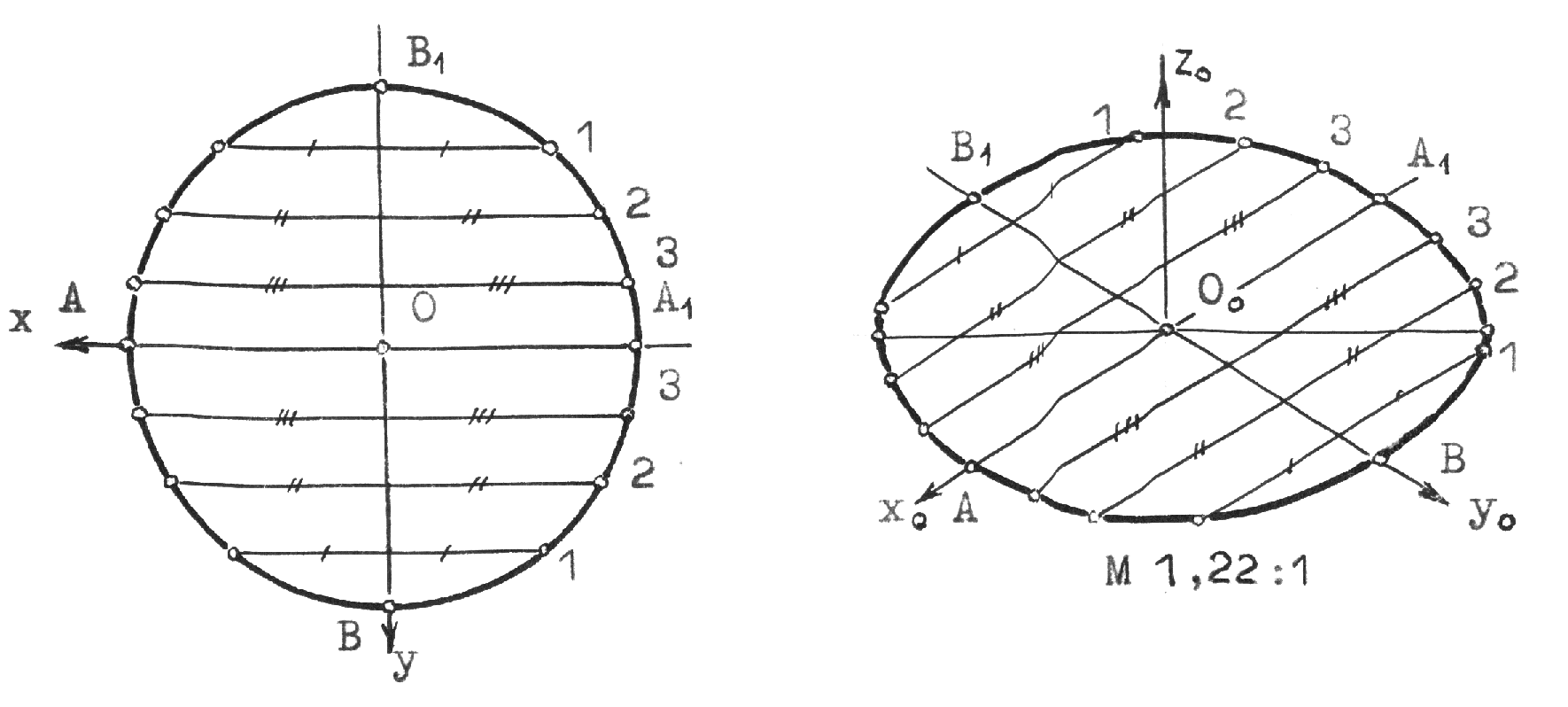 Рис.10.10 Рис.10.11 При желании получить изображение окружности в изометрии в масштабе 1:1, необходимо при выполнении изометрической проекции, умножить величины координат на 0,82. Для этой цели можно воспользоваться равнобедренным треугольником с соотношением боковых сторон к основанию как 100:82 (рис.10.12; 10.13). 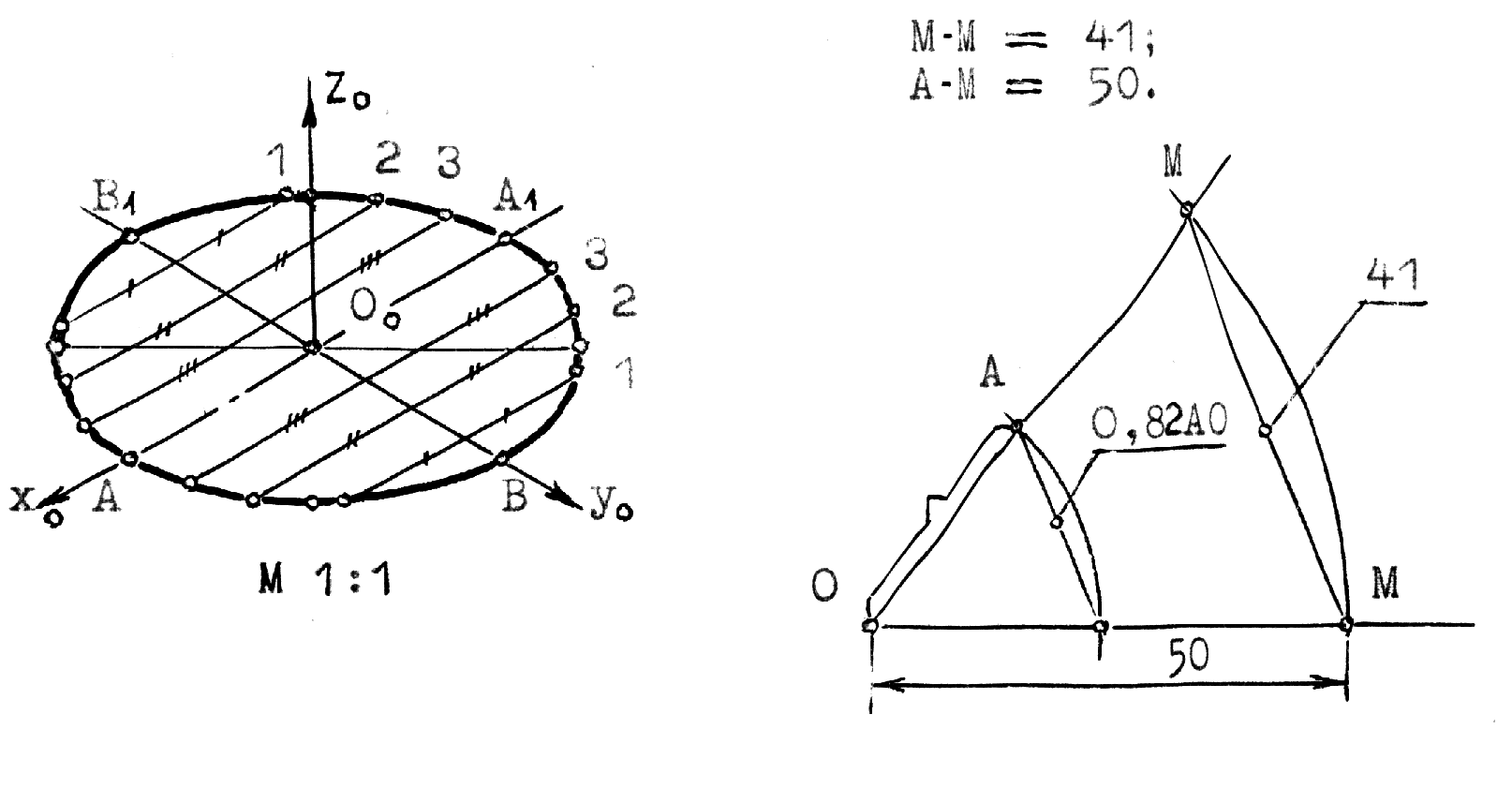 Рис.10.12 Рис.10.13 ИЗОБРАЖЕНИЕ ОКРУЖНОСТЕЙ В КООРДИНАТНЫХ ПЛОСКОСТЯХ ДИМЕТРИЧЕСКОЙ ПРОЕКЦИИ Пример 2 (рис.10.14, 10.15, 10.16). Построить изображения окружностей в координатных плоскостях 00х0z0 и 00у0z0 прямоугольной диметрической проекции. Диаметр окружности - 50 мм. 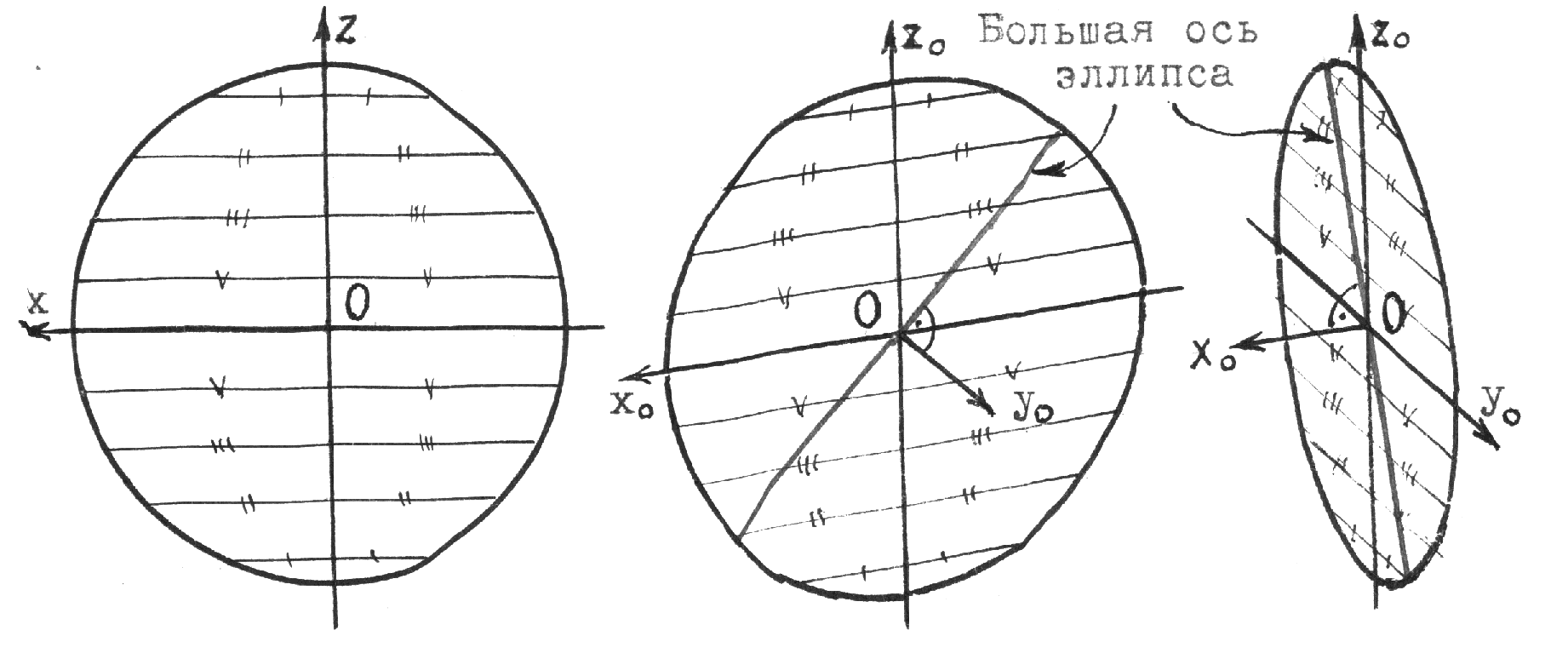 Рис.10.14 Рис.10.15 Рис.10.16. ПОСТРОЕНИЕ АКСОНОМЕТРИЧЕСКИХ ИЗОБРАЖЕНИЙ ПРОСТЕЙШИХ ГЕОМЕТРИЧЕСКИХ ТЕЛ И ЗАДАНИЕ ТОЧЕК НА ИХ ПОВЕРХНОСТЯХ Пример 1 (рис.10.17, 10.18 и 10.19). Построить изометрическую и диметрическую проекции заданного прямого кругового конуса. 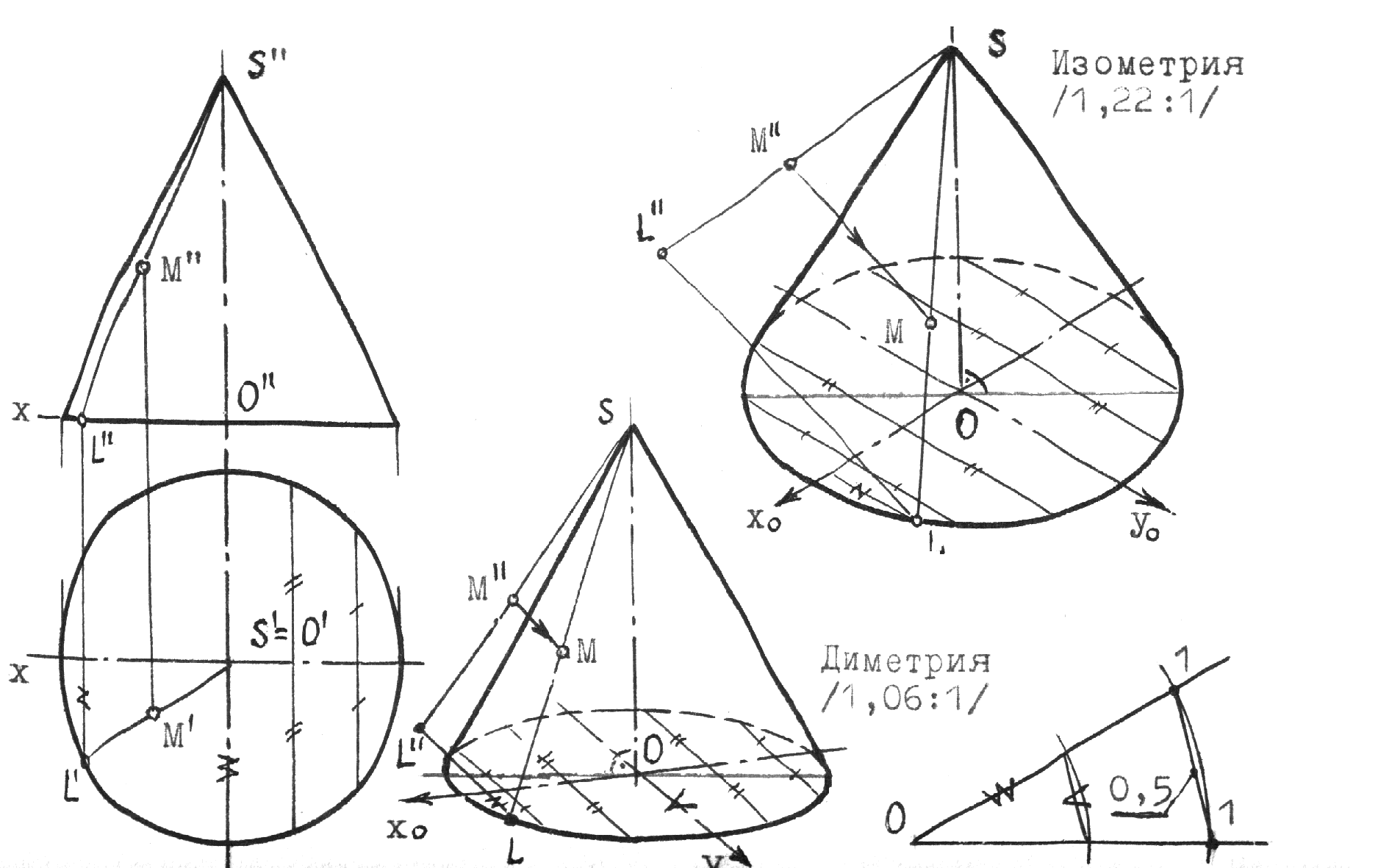 Рис.10.17 Рис.10.19 Помимо стандартных прямоугольных изометрической и диметрической проекций не запрещены и прямоугольные триметрические проекции, выбор которых возможен как вариант п.5 (рис.10.5). Приведем одну из триметрических прямоугольных проекций. Триметрическая проекция Ю.А. Михалева, которую он использовал в своей инженерной практике, составляя технические описания. В этой триметрической проекции использованы стандартные углы чертежных инструментов: 150, 300 и 450, которые при выборе того или иного их сочетания, позволяют получить три типа триметрических проекций, плюс их симметричные отображения. На рис.10.20 изображен куб в триметрии Ю.А. Михалева, варианты расположения осей которого показаны отдельно на рисунках 10.21, 10.22, 10.23. 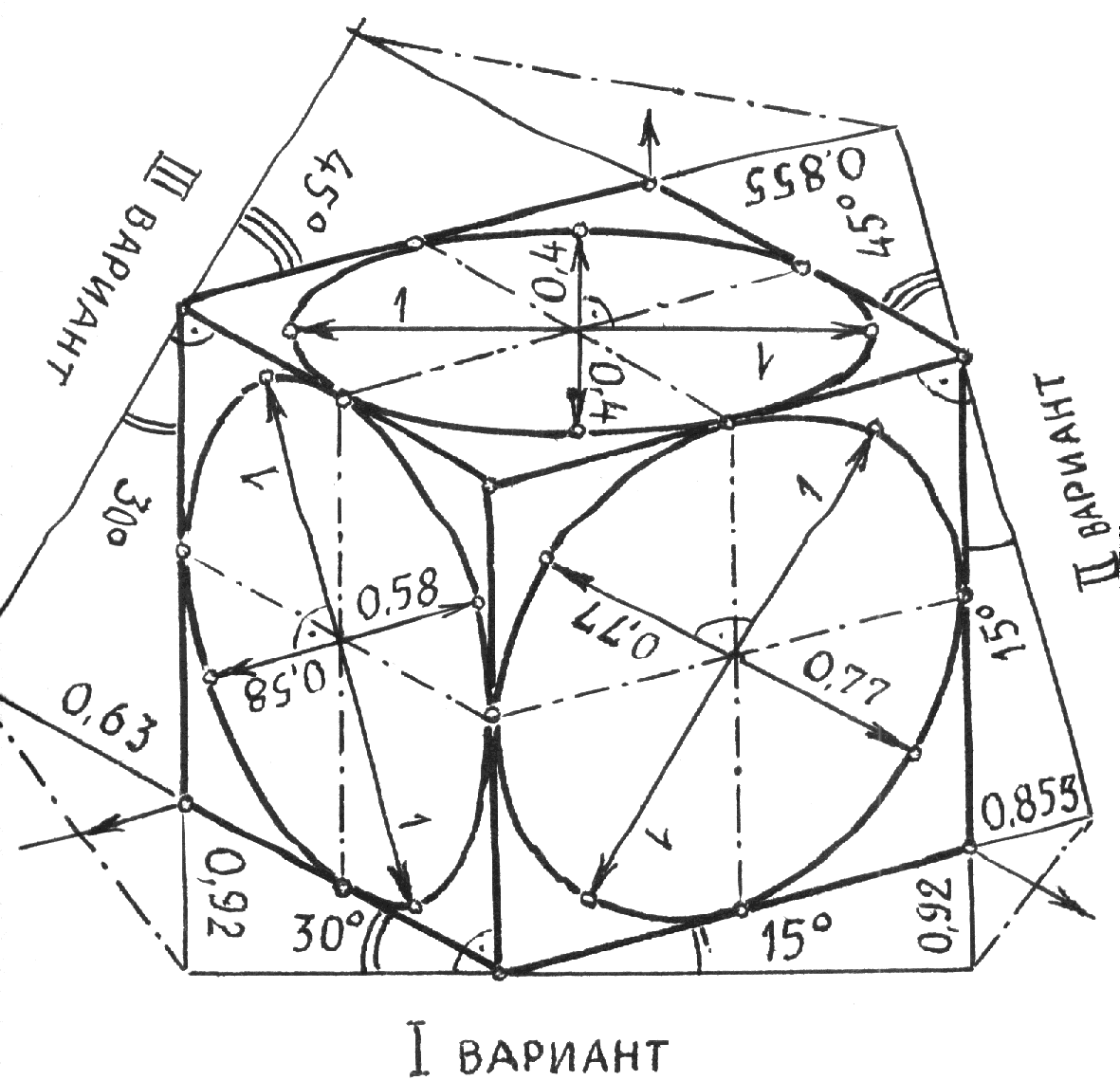 Рис.10.20 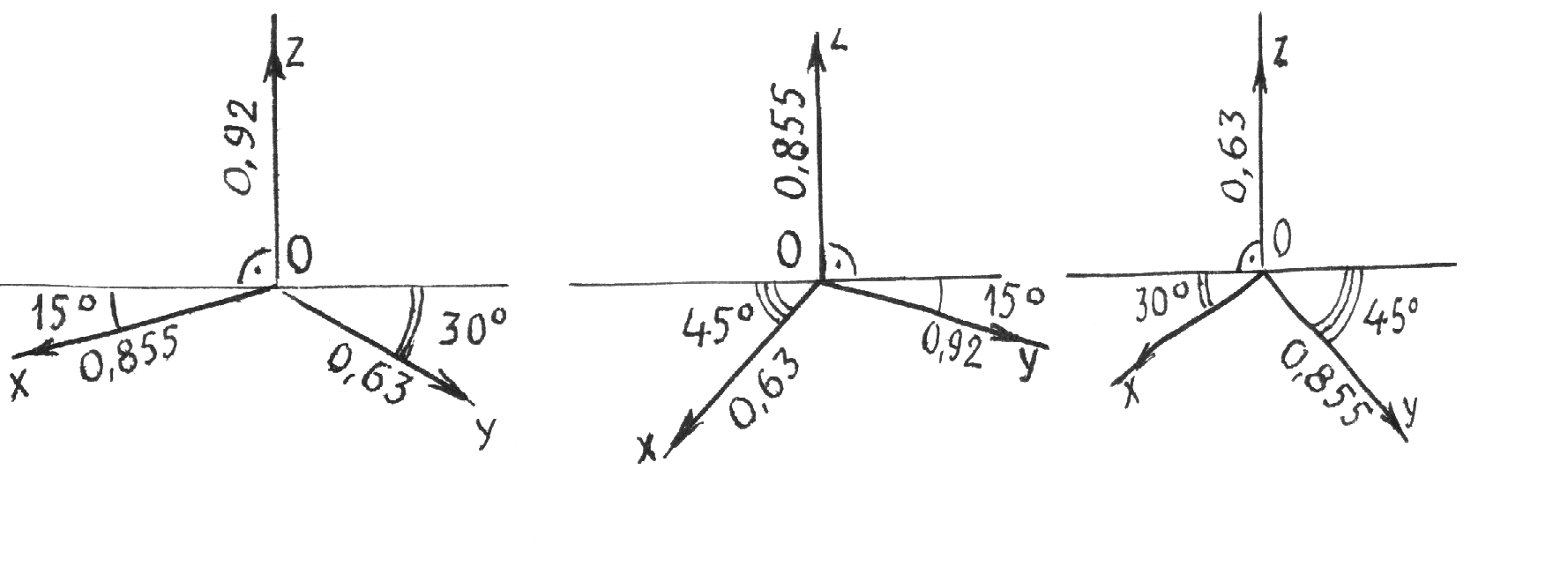 Рис.10.21 Рис.10.22 Рис.10.23 11. ПЛОСКОСТИ И ПРЯМЫЕ, КАСАТЕЛЬНЫЕ К КРИВЫМ ПОВЕРХНОСТЯМ 1. Проведение касательных к плоским кривым линиям. 1.1. Проведение касательной из внешней точки к окружности (рис.11.01). 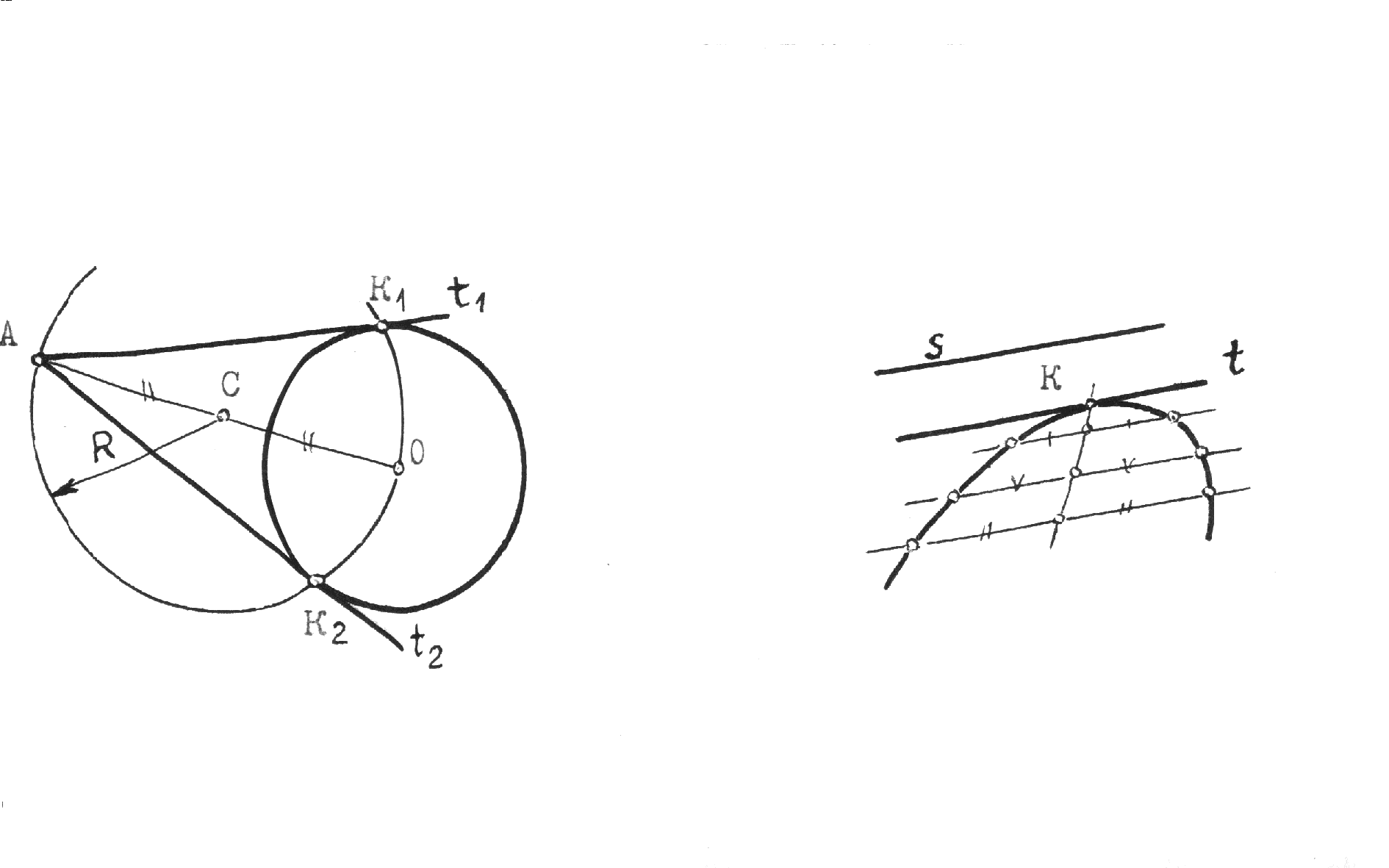 Рис.11.01 Рис.11.02 1.2. Проведение касательной к кривой линии, параллельной направлению s (рис.11.02). 1.3. Проведение касательной из внешней точки А к кривой второго порядка. На рис.11.03 проведены касательные к эллипсу из внешней точки А. Решение: Это построение основано на теории поляр. Точка А - полюс (Р), линия р - поляра этого полюса. Чтобы получить точки К1 и К2 касания касательных t1 и t2, проводим из точки А три секущих, пересекающих эллипс соответственно в точках 1 и 2, 3 и 4, 5 и 6. Дальнейшее построение понятно из чертежа. Поляра р пересечет очерк эллипса в точках К1 и К2. Касательные t1 и t2 определены. 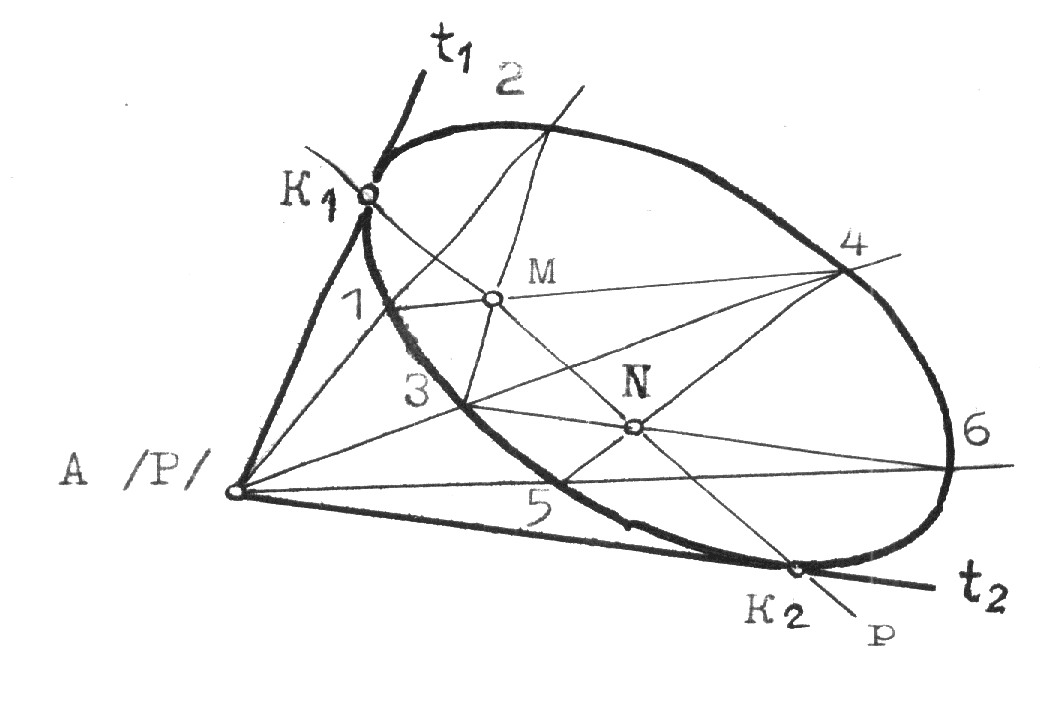 Рис.11.03 1.4. Касательные к пространственной кривой линии. Теорема: Проекция касательной к пространственной кривой линии является в общем случае касательной к проекции этой кривой линии (рис.11.04, 11.05). 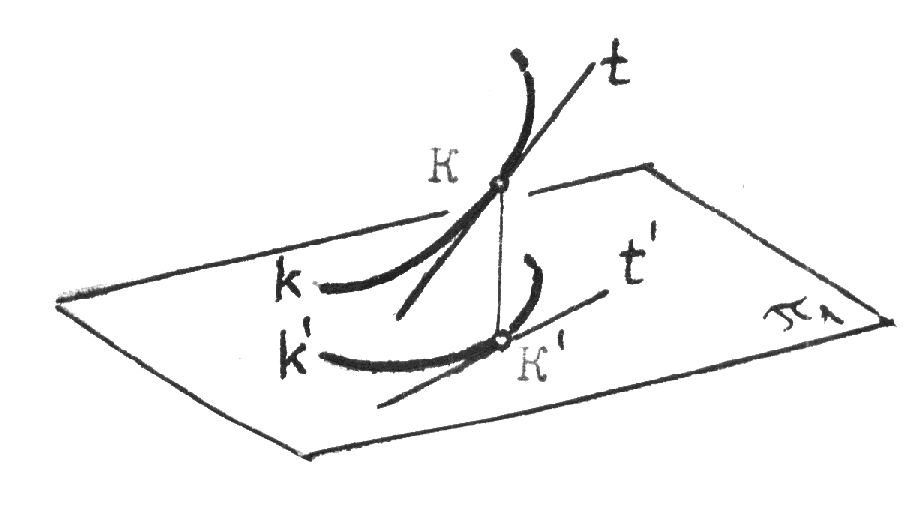 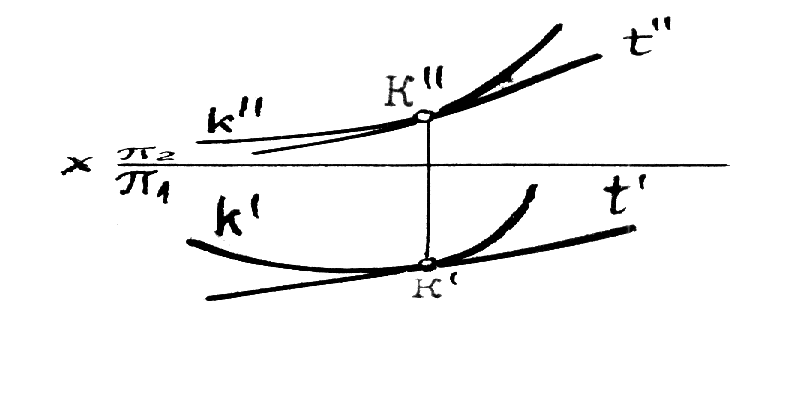 Рис.11.04 Рис.11.05 1.5 ПЛОСКОСТИ И ПРЯМЫЕ, КАСАТЕЛЬНЫЕ К КРИВОЙ ПОВЕРХНОСТИ В ДАННОЙ ТОЧКЕ Для построения плоскости, касательной к кривой поверхности в данной точки К, достаточно провести через эту точку на поверхности две пересекающиеся инструментально простые линии. Такими линиями могут быть две линии каркаса поверхности, например, параллель и меридиан на поверхности вращения. Проведя касательные к каждой из этих кривых линий, получим две пересекающиеся прямые, определяющие одну и только одну плоскость , касательную к данной поверхности в точке К, если данная точка является “гладкой точкой” поверхности. Любая прямая лежащая в касательной плоскости и проходящая через точку касания К, будет касательной к заданной поверхности в этой точке. Прямая n, проходящая через точку К и перпендикулярная к касательной плоскости , являются нормалью поверхности в точке К. На рис.11.06, для иллюстрации, через точку К проведены две кривые линии, принадлежащие некоторой выпуклой поверхности. 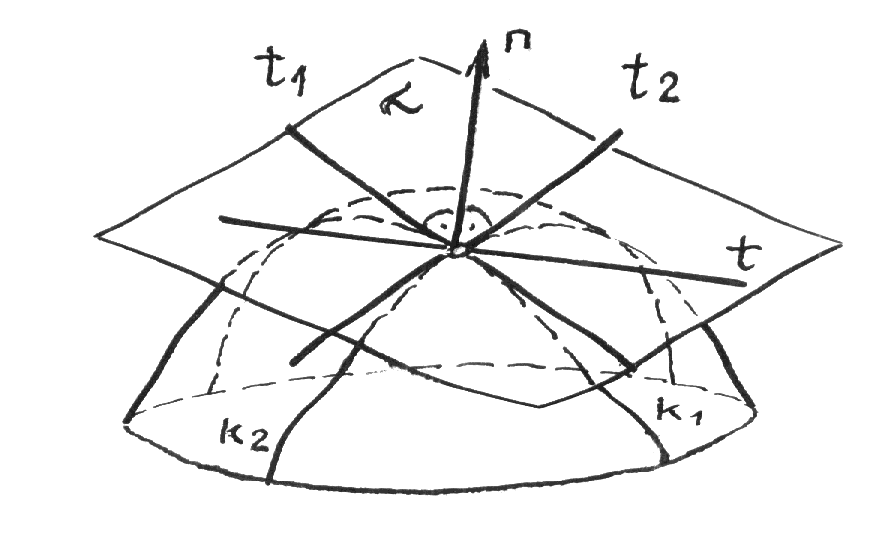 Рис.11.06 1.6. ПРИМЕРЫ ПОСТРОЕНИЯ ПЛОСКОСТЕЙ, КАСАТЕЛЬНЫХ К НЕКОТОРЫМ КРИВЫМ ПОВЕРХНОСТЯМ Плоскость, касательная к поверхности цилиндра или конуса, определяется образующей поверхности, по которой происходит касание, и прямой, касательной к кривой основания поверхности в точке пересечения этой образующей (рис.11.07). 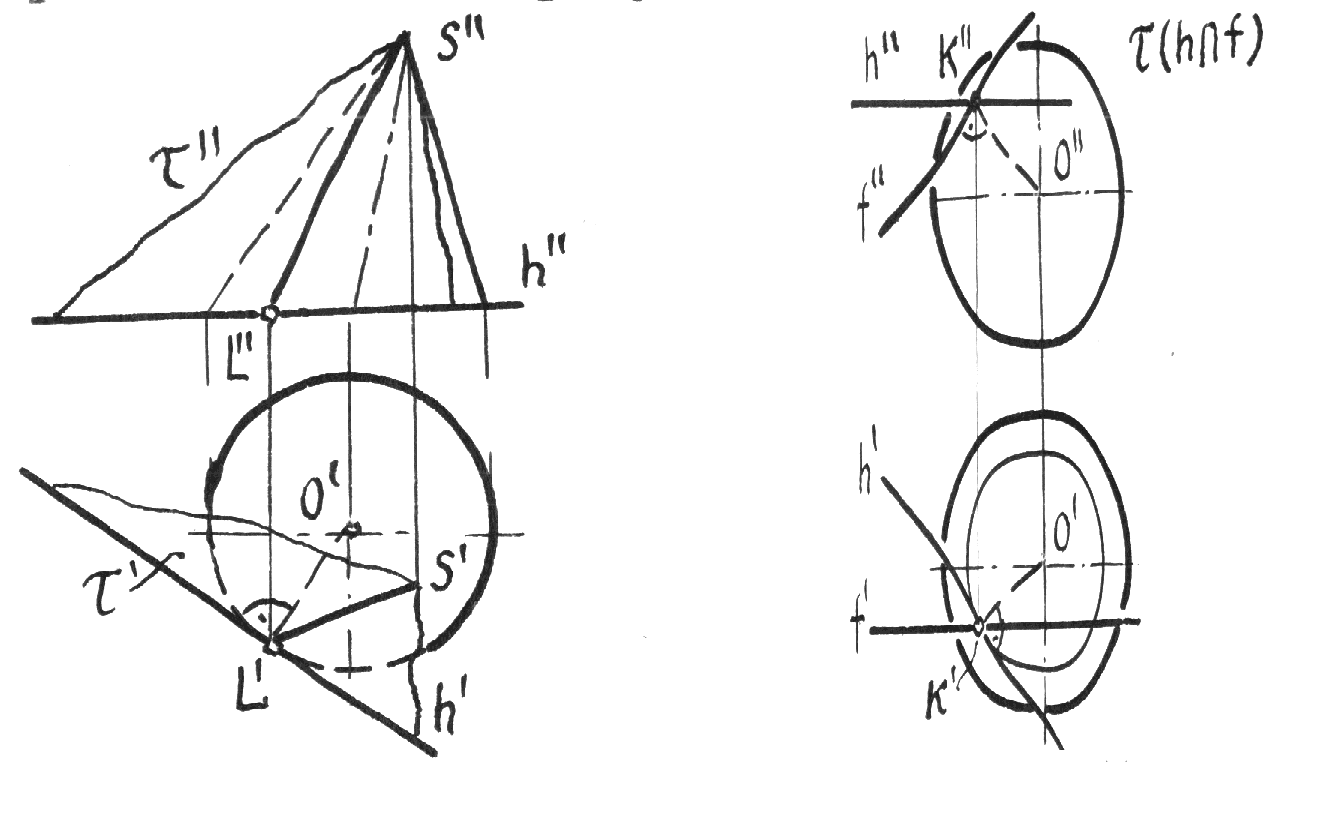 Рис.11.07 Рис.11.08 Плоскость, касательная к сфере в некоторой точке К, перпендикулярна к радиусу сферы, проведенному в эту точку касания (рис.11.08). 1.7. ПРИМЕРЫ ПОСТРОЕНИЯ ПРЯМЫХ, КАСАТЕЛЬНЫХ К КРИВЫМ ПОВЕРХНОСТЯМ В ДАННОЙ ТОЧКЕ Пример 1 (рис.11.09). Найти горизонтальную проекцию прямой t, касательной к поверхности конуса в точке К. Решение: Чтобы построить прямую, касательную к кривой поверхности в данной точке, нужно сначала построить плоскость, касательную к поверхности в данной точке, а затем провести в этой плоскости искомую касательную. Построение касательной плоскости рассмотрено нами выше на рис.11.07. Построение понятно из чертежа. Касательная определяется точками К и М. 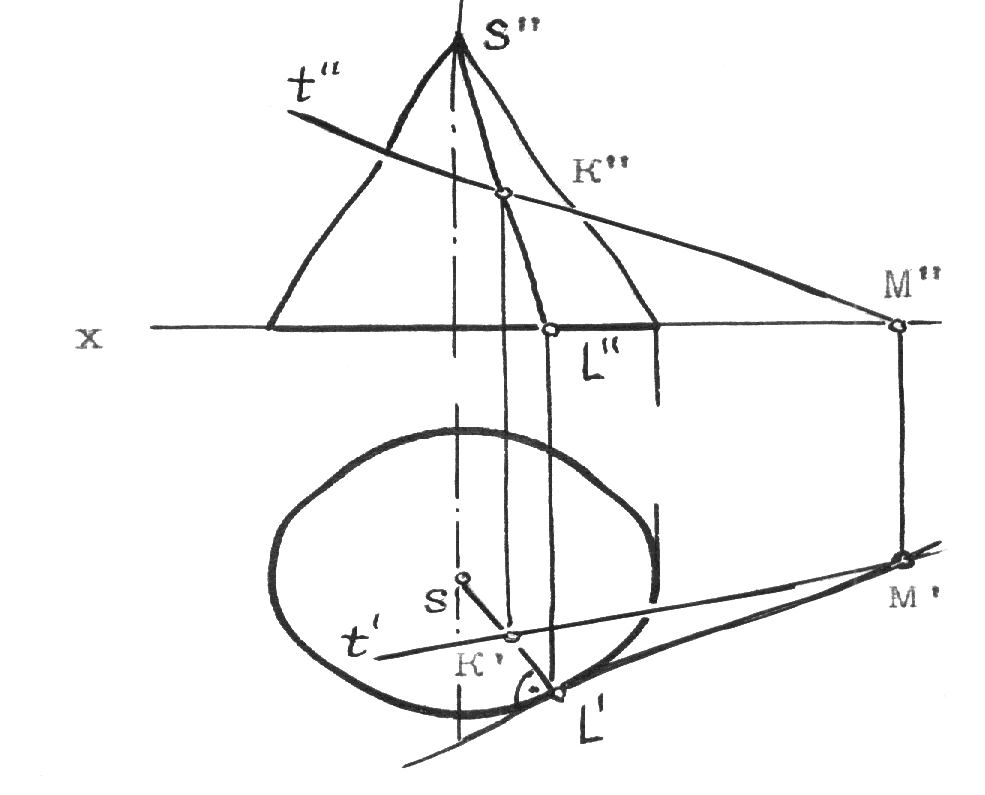 Рис.11.09 Пример 2 (рис.11.10). Через точку А провести фронтальную прямую, касательную к цилиндрической поверхности вращения. Решение задачи ясно из чертежа. Плоскость касается цилиндрической поверхности вращения по образующей, проходящей через точку К, найденную преобразованием чертежа. 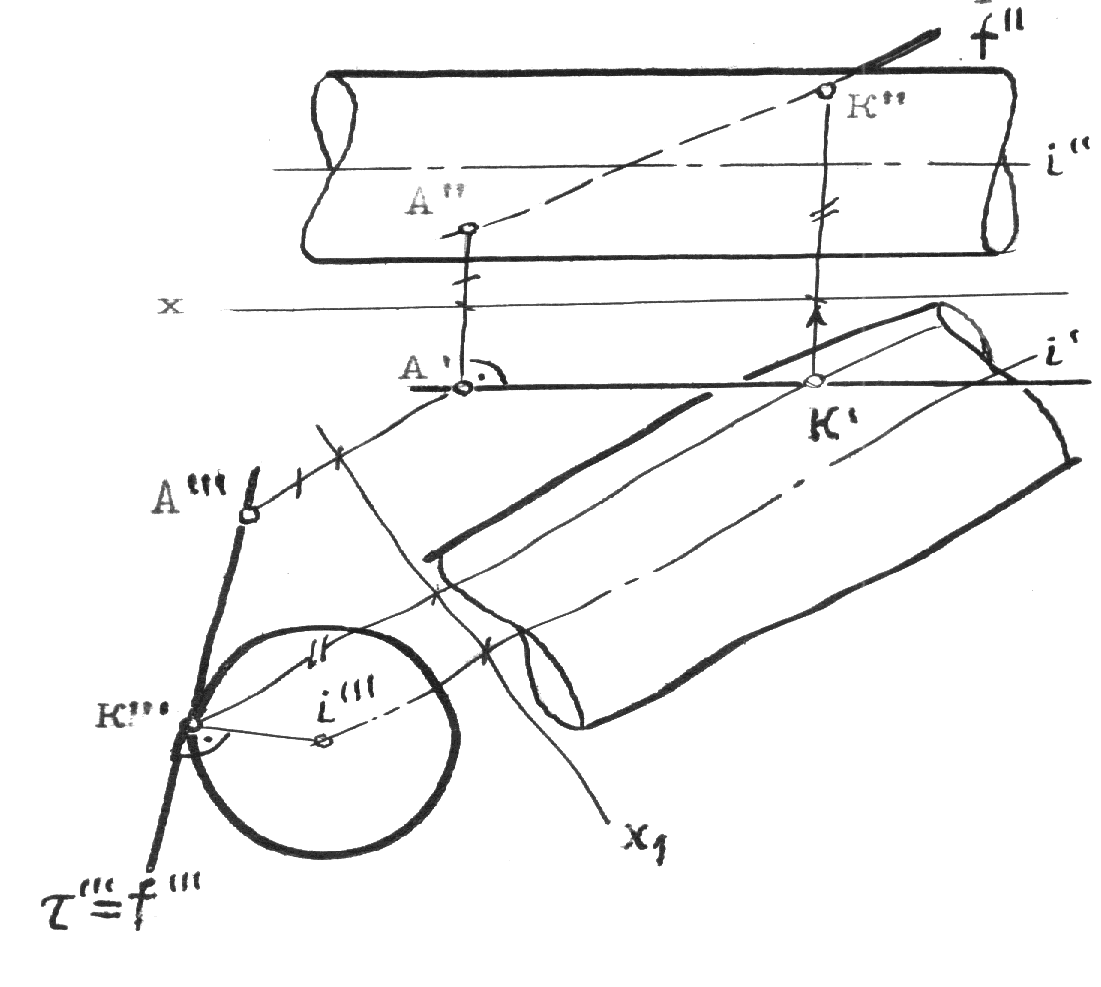 Рис.11.11 11.08. ВЗАИМНОЕ КАСАНИЕ КРИВЫХ ПОВЕРХНОСТЕЙ Если две кривые поверхности соприкасаются в некоторой точке, то они имеют общую касательную плоскость, проходящую через эту точку (рис.11.12). 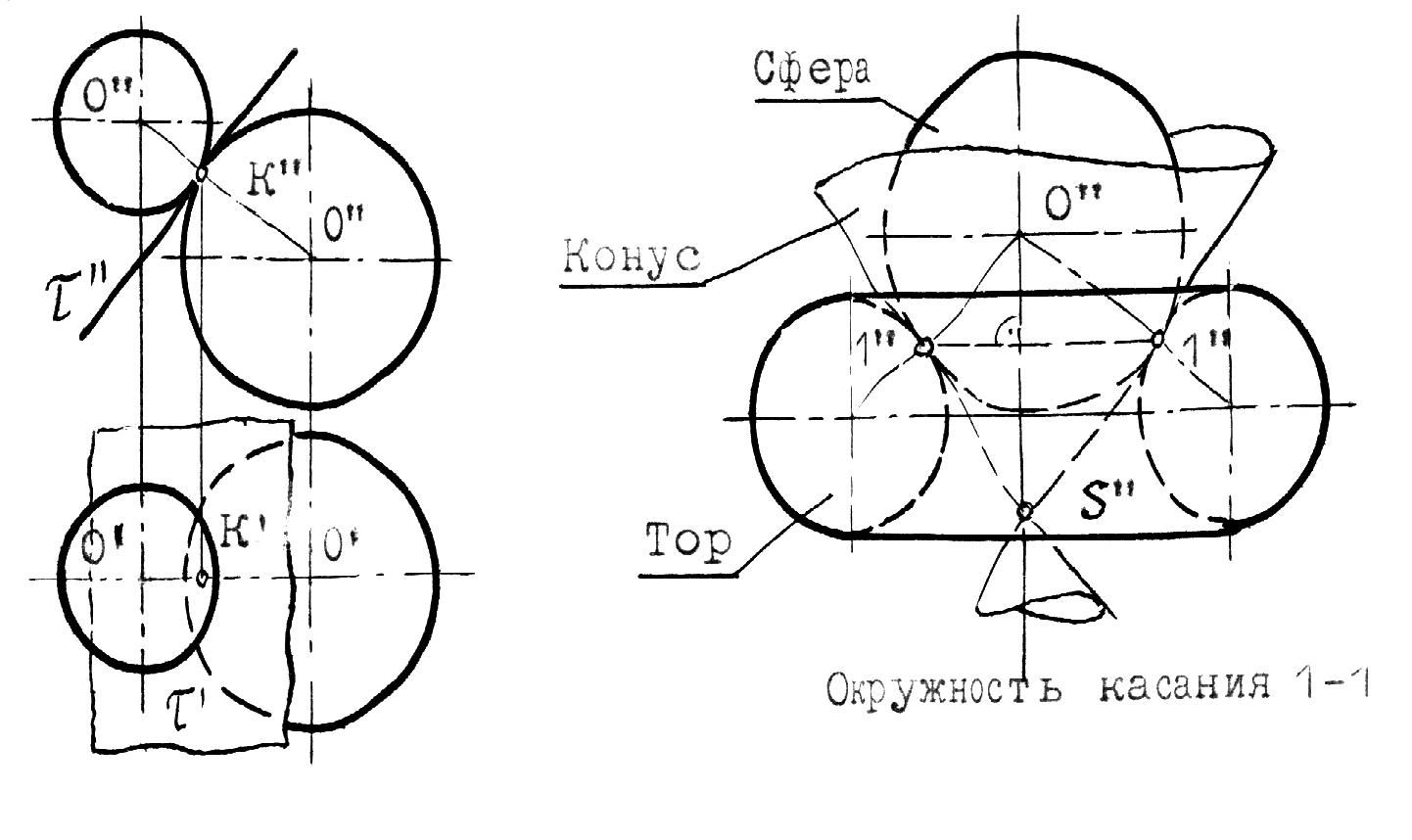 Рис.11.12 Рис.11.13 Если две кривые поверхности касаются по некоторой плоской кривой, то они имеют общую касательную коническую или цилиндрическую поверхность, проходящую через эту кривую. (рис.12.13). Пример 1 (рис.11.14). Найти фронтальную сферы, касательной к поверхности тора. Решение: Центр 0 искомой сферы удален от поверхности тора на расстояние R, равном сумме радиусов сферы и радиуса меридиана тора. Повернув сферу вокруг оси тора до положения ее центра 0 в плоскости главного меридиана тора, получим возможность найти точку касания К (К``). обратным преобразованием найдем искомое положение сферы (проекции 0``центра сферы и точки K`` касания). Ход решения задачи указан стрелками. 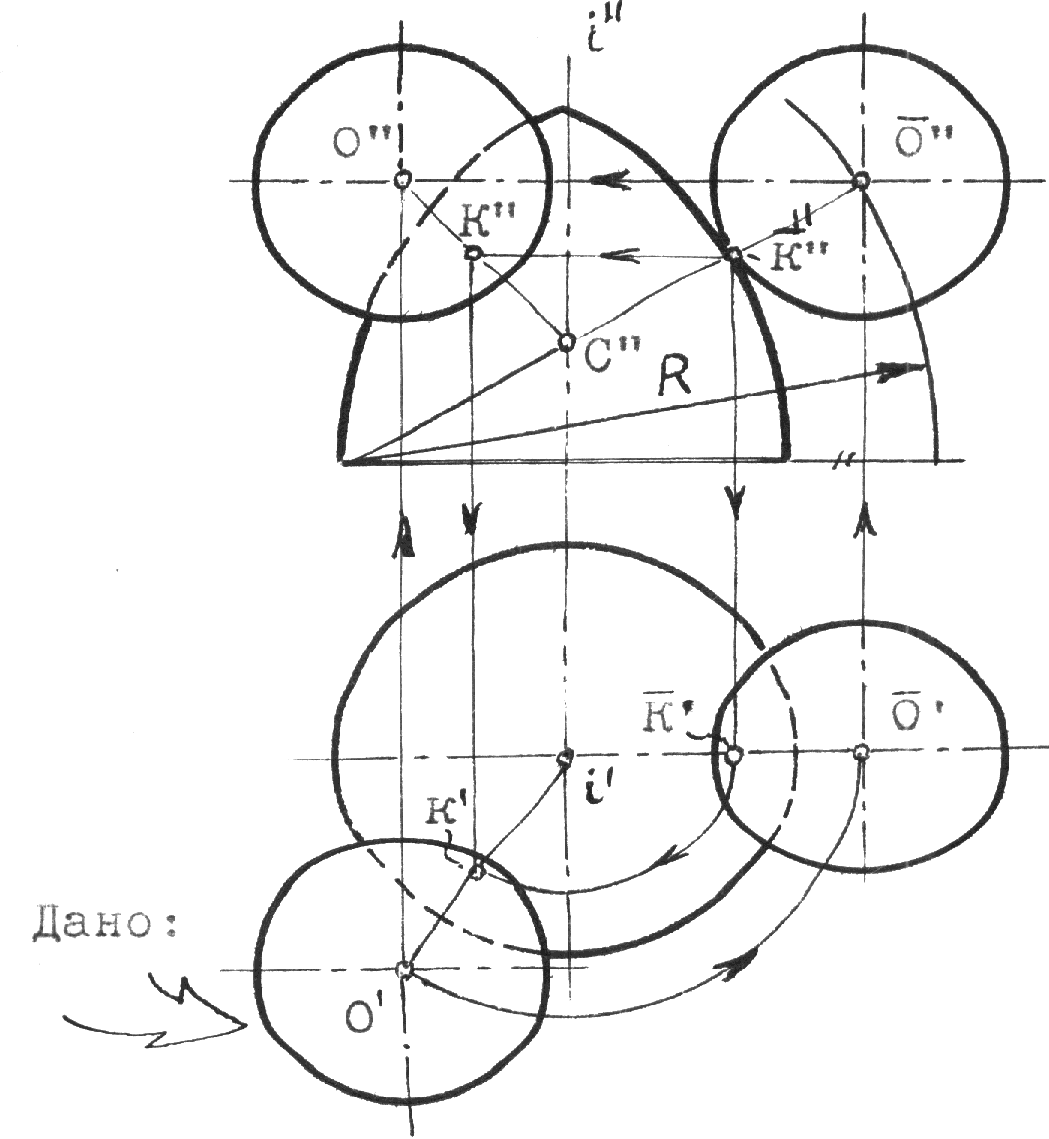 Рис.11.14 12. ПОСТРОЕНИЕ ГЕОМЕТРИЧЕСКИХ МЕСТ И ИХ ПРИМЕНЕНИЕ К РЕШЕНИЮ ЗАДАЧ Геометрическое место есть совокупность точек, положение которых удовлетворяет некоторым геометрическим условиям. Решение геометрических задач часто сводится к построению геометрических мест: требуется найти точки, линии и другие геометрические образы, удовлетворяющие тем или иным заданным условиям. Для каждого условия строится свое геометрическое место и затем берется сочетание этих геометрических мест. Ниже перечисляются важнейшие геометрические места, к нахождению которых приводится решение многих задач.
Если провести плоскость, пересекающую конус перпендикулярно к его оси, то поверхность конуса будет служить геометрическим местом прямых, проходящих через вершину и наклоненных к этой плоскости под углом 900-0. Всякая плоскость, касательная к такому конусу, будет наклонена под углом 900-0 к этой плоскости нормального сечения конуса.
ПРИМЕРЫ ПРИМЕНЕНИЯ СПОСОБА ГЕОМЕТРИЧЕСКИХ МЕСТ Пример 1 (рис.12.1). Построить точку В по ее координатам у=m, z=n и R от точки А. 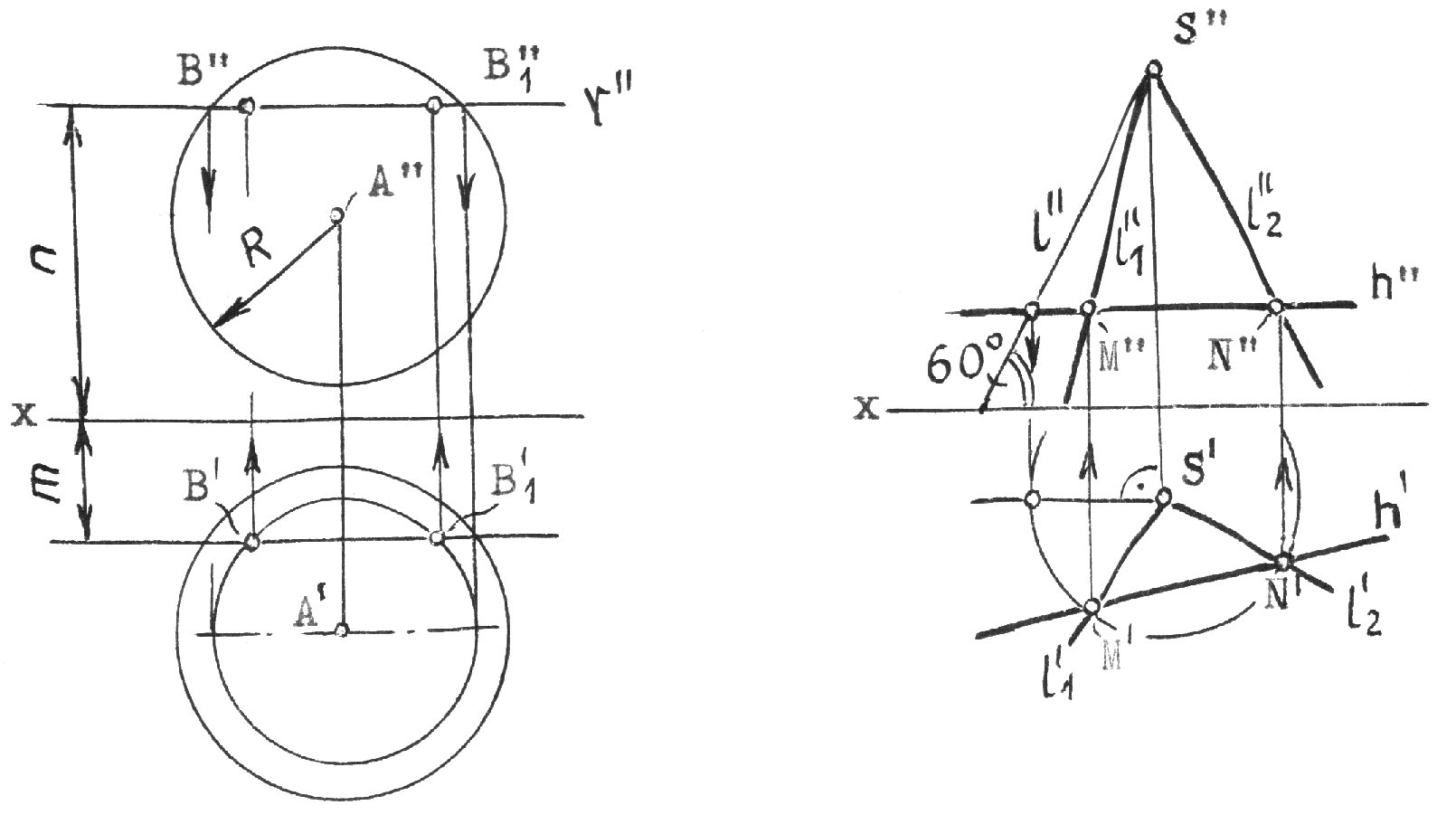 Рис.12.1 Рис.12.2 Пример 2 (рис.12.2). Через точку S провести прямую l, наклоненную к горизонтальной плоскости проекций под углом 600 и пересекающую прямую h. Литература: Бубенников А.В. Начертательная геометрия: Учебник для втузов. - 3-е изд., перераб. и доп. - М.:Высш.шк., 1985, 288с. Гордон В.О., Семенцев-Огиевский М.А. Курс Начертательной геометрии: Учеб. пособие (Под ред. Ю.Б.Иванова. -23 изд., перераб. М.: Наука. Гл. ред. физ.-мат. лит., 1988, -272 с. ил. Локтев О.В. Краткий курс начертательной геометрии: Учебник для втузов. - 2-е изд., перераб. и доп. -М:Высш.шк.,1985, 136 с., ил. Фролов С.А. Начертательная геометрия: Учебник для втузов. - 2-е изд., перераб. и доп. - М.: Машиностроение, 1989, 240 с. ил. ___________________________________________________________ Рыжов Н.Н. Образование поверхностей и их задание на комплексном чертеже. Метод. указан. по курсу начертательной геометрии. Изд.МАДИ, -М.: 1983. Рыжов Н.Н. Главные позиционные задачи. Метод.указан. по курсу начертательной геометрии. Изд МАДИ, М.: 1984. Рыжов Н.Н. Метрические задачи. “Преобразование комплексного чертежа”. Метод. указан. по курсу “Начертательная геометрия”. Изд. МАДИ. -М.: 1985. |
