9 СОЧ -1. 9 СОЧ-1 Алгебра. 9. 1а уравнения, неравенства с двумя переменными и их системы

• Название: 9. 1а уравнения, неравенства с двумя переменными и их системы
• Анкор: 9 СОЧ -1
• Дата: 14.02.2023
• Размер: 20.1 Kb.
• Имя файла: 9 СОЧ-1 Алгебра.docx
• Тип: Документы; #936141

Алгебра 9 класс СОЧ -1

Тема:

9.1А Уравнения, неравенства с двумя переменными и их системы

9.1В Элементы комбинаторики

Цели обучения:

9.2.2.1 различать линейные и нелинейные уравнения с двумя переменными;

9.2.2.2 решать системы нелинейных уравнений с двумя переменными;

9.4.2.1 решать текстовые задачи с помощью систем уравнений;

9.4.3.1 составлять математическую модель по условию задачи;

9.2.2.3 решать неравенства с двумя переменными;

9.2.2.4 решать системы нелинейных неравенств с двумя переменными

6.1.2.11 изображать подмножества рациональных чисел с помощью кругов Эйлера-Венна;

9.3.1.6 знать и применять формулу бинома Ньютона и его свойства;

Критерии оценивания:

- различает линейные и нелинейные уравнения с двумя переменными;

-решает системы нелинейных уравнений с двумя переменными;

- решает текстовые задачи с помощью систем уравнений;

- составляет математическую модель по условию задачи;

- решает неравенства с двумя переменными;

- решает системы нелинейных неравенств с двумя переменными

- изображает подмножества рациональных чисел с помощью кругов Эйлера-Венна;

-знает и применяет формулу бинома Ньютона и его свойства;

-решает задачи, используя формулы комбинаторики;

- решает уравнения, используя правило комбинаторики

СОЧ №1, Алгебра 9 класс, I вариант

1.Решите систему уравнений: 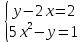(5 балла)

2.Изобразите множество точек, заданных системой неравенст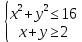в:

(5 баллов)

3. Два насоса, работая вместе , могут заполнить бассейн за 4 часа. Первый насос заполнит бассейн за 12 часов. За сколько часов заполнит бассейн второй насос?

(5 баллов)

4. В классе 10 юношей и 8 девушек занимаются спортом. Сколькими способами можно составить из них команду для участия в соревнованиях в составе

4 юношей и 3 девушек? (5 баллов)

СОЧ №1, Алгебра 9 класс, II вариант

1.Решите систему уравнений: 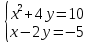; (5 баллов)

2.Изобразите множество точек, заданных системой неравенст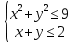в:

(5 баллов)

3. Два насоса , работая вместе, заполнят бассейн за 12 часов. Первый бассейн в 1,5 раза быстрее, чем второй. За сколько часов заполняет бассейн первый насос? (5 балла)

4. В классе 10 юношей и 8 девушек занимаются спортом. Сколькими способами можно составить из них команду для участия в соревнованиях в составе

4 юношей и 4 девушек? (5 баллов)

СОЧ I четверть Алгебра

Критерии оценивания		№ задания	Дескрипторы	Балл
Применяет методы решения систем нелинейных уравнений с двумя переменными		1	Выражает одну переменную через другую	1
			Использует метод подстановки	1
			Решает полученное уравнение	1
			Находит решения системы уравнений	1
			Запишет правильно ответ	1
Решает системы нелинейных неравенств с двумя переменными		2	Изображает множество решений неравенства 1	2
			Изображает множество решений неравенства 2	2
			Показывает пересечение множеств решений неравенств	1
Составляет уравнение для решения текстовых задач	3		Запишет краткое условие	1
			Составляет уравнение	1
			Решает уравнение	2
			Записывает ответ соответствии условием задачи	1
Решает задачу с применением правил комбинаторики		4	Применяет формулу сочетания без повторений для нахождения 4 юношей из 10. Вычисляет	2
			Применяет формулу сочетания без повторений для нахождения 3 (4) девушек из 8. Вычисляет	1
			Применяет правило сложения комбинаторики и вычисляет число сложения комбинаторики	2
			Всего баллов	20