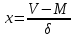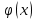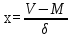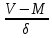А. А. Ежевского институт управления природными ресурсами факультет охотоведения имени в. Н. Скалона биометрия в ихтиологии методические указания

Название	А. А. Ежевского институт управления природными ресурсами факультет охотоведения имени в. Н. Скалона биометрия в ихтиологии методические указания
Дата	29.08.2022
Размер	100.79 Kb.
Формат файла
Имя файла	Biometriya_v_ihtiologii_1599447944.docx
Тип	Методические указания #655640
страница	4 из 7

1 2 3 4 5 6 7

Вариант 7:

Определить: величины моды и медианы для вариационного ряда массы хариуса сибирского Полярного Урала возраста 5+ если отдельные измерения дали следующие результаты (г):

416; 407; 367; 325; 495; 415; 575; 360; 377; 433; 543; 516; 432; 448; 360; 402; 365; 406; 470; 378; 370; 369; 362; 406; 418; 375; 496; 411; 381; 379; 386; 171; 390; 405; 415.

Вариант 8:

Определить: величины моды и медианы для вариационного ряда массы байкальского омуля возраста 10+ если отдельные измерения дали следующие результаты (г):

497; 577; 537; 454; 551; 555; 495; 575; 543; 516; 470; 496; 553; 564; 568; 503; 505; 497; 512; 545; 566; 569; 573; 542; 554; 498; 478; 466; 545; 549; 560; 534; 543; 518; 530; 514; 502; 565; 569; 535.

Вариант 9:

Определить: величины моды и медианы для вариационного ряда массы ленка возраста 4+ р. Лена если отдельные измерения дали следующие результаты (г):

225; 287; 354; 345; 457; 356; 372; 364; 351; 376; 350; 359; 105; 210; 117; 260; 485; 490; 401; 415; 295; 370; 385; 371; 386; 398; 405; 218; 177; 185; 109; 340; 353; 359; 362; 355; 404.
Задание 4. Определение средней квадратической

Ход выполнения задания

Средняя квадратическая используется для признаков, которые характеризуются площадью круга и для ее получения измеряют величину диаметра. Вычисляют по формуле: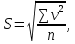

S – средняяквадратическая;

v - значение варьирующего признака;

n – число наблюдений.

Определяют в тех же единицах измерения, что и исходные данные.

Вариант 0:

Определить:средний диаметр эритроцитов (мкм):

7, 8, 10, 8, 11, 6, 12, 7, 9, 8, 10, 12, 6, 9, 8, 12, 10, 7, 12, 11, 14, 7, 13, 11, 6, 9, 8.

Вариант 1:

Определить:средний диаметр ядра в животных клетках(в μ):

225, 144, 400, 484, 324, 225, 402, 361, 289, 196, 199, 144, 277, 167, 186, 170.

Вариант 2:

Определить:средний горизонтальный диаметрглаза атлантического лосося возраста 3+ малых рек бассейна Белого моря (мм):

6,6; 6,9; 4,7; 8,9; 7,3; 5,9; 8,2; 7,4; 9,1; 6,8; 5,1; 8,1; 6,8; 5,8; 8,2; 7,7; 6,4; 5,5; 4,9.

Вариант 3:

Определить:средний диаметр икринок леща р.Ишим (мм):

0,77; 0,84; 1,40; 0,94; 0,70; 0,88; 1,12; 1,36; 1,19; 1,22; 1,38; 1,16; 1,25; 1,16; 1,31.

Вариант 4:

Определить:средний диаметр икринок озерной пеляди (мм):

1,99; 2,03; 2,04; 2,08; 2,11; 2,12; 2,15; 2,12; 2,05; 2,20; 2,14, 2,07; 1,95; 2,13; 2,21; 2,14.

Вариант 5:

Определить:средний горизонтальный диаметрглаза горбуши Западной Камчатки (мм):

10,5; 11,7, 12,6; 13,8; 9,5; 11,5; 14,3; 12,1; 15,0; 9,9; 10,4; 14,7; 10,8; 14,4; 14,6; 12,9; 11,1.

Вариант 6:

Определить:средний горизонтальный диаметрглаза окуня водоемов Пермского края (мм):

7,68; 7,74; 7,80; 7,58; 7,55; 7,81; 7,65; 7,60; 7,48; 7,40; 7,53; 7,88; 7,84; 7,66; 7,77; 7,44; 7,65.

Вариант 7:

Определить:средний горизонтальный диаметрглаза щуки Вилюйского водохранилища (мм):

10, 6; 10,2; 8,7; 11,7; 11,2; 10,9; 9,6; 9,0; 10,4; 11,1; 11,9; 9,9; 12,0; 10,5; 10,9; 11,4; 9,5; 9,3.

Вариант 8:

Определить:средний горизонтальный диаметрглаза муксуна р. Лена (мм):

15,5; 16,7; 16,5; 12,0; 17,7; 14,1; 16,2; 15,0; 16,9; 13,8; 14,9; 12,5; 17,1; 15,6; 12,6; 14,5; 15,5; 15,8.

Вариант 9:

Определить:средний горизонтальный диаметрглаза гольца р. Лена (мм):

15,5; 22,0; 14,0; 12,9; 12,0; 17,3; 15,8; 16,0; 15,7; 14,5; 14,8; 13,9; 16,6; 14,2; 15,6; 15,1.

Задание 5. Определение степень трансгрессии двух вариационных рядов

Ход выполнения задания

Трансгрессивными рядами и кривыми называются ряды, которые отличаются друг от друга величиной средней арифметической и у которых крайние классы, лежащие около максимального класса первой кривой, служат минимальными классами другой кривой, что создает в этих частях вариационных кривых их взаимное пересечение.

При изучении трангрессирующих рядов требуется решить следующие задачи:

Определить степень трансгрессии.
Определить, достоверна ли разность между средними арифметическими каждого ряда если разница между М₁ и М₂ достоверна, то это доказывает наличие двух трангрессирующих рядов.
Определить, к какому из рядов следует отнести конкретную особь, которая имеет признак на уровне вариантов, отчленяющих пересекающиеся части обоих рядов.

Определение степени трансгрессии проводится по следующей формуле: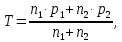

Т – степень трансгрессии;

n₁и n₂ – общее число наблюдений в каждой из выборок;

р₁ и р₂ – доля трансгрессирующих частот в каждом из рядов,

ограниченных площадью кривой между Vмин₂ и Vмакс₁.

В формуле трангрессии требуется найти доли трансгрессирующих частот р₁ и р₂. Для этого используется вторая функция нормированного отклонения.

Площади и ординаты нормальной кривой распределения (из Миллса)

Нормированное отклонение	Вторая функция нормированного оклонения		Первая функция нормированного отклонения f (x) ордината у при значениях То есть вероятность у_х при отклонениях V от М на х
Нормированное отклонение	Площадь между ординатами у_о и у	% числа наблюдений, заключенных между ординатами у₀ и у
0,0	0,00000	0	0,39894
0,1	0,03983	3,983	0,39695
0,2	0,07926	7,926	0,39104
0,3	0,11791	11,791	0,38139
0,4	0,15542	15,542	0,36827
0,5	0,19146	19,146	0,35207
0,6	0,22575	22,575	0,33322
0,7	0,25804	25,804	0,31225
0,8	0,28814	28,814	0,28969
0,9	0,31594	31,594	0,26609
1,0	0,34134	34,134	0,24197
1,1	0,36433	36,433	0,21785
1,2	0,38493	38,493	0,19419
1,3	0,40320	40,320	0,17137
1,4	0,41924	41,924	0,14973
1,5	0,43319	43,319	0,12952
1,6	0,44520	44,520	0,11092
1,7	0,45543	45,543	0,09405
1,8	0,46407	46,407	0,07895
1,9	0,47128	47,128	0,06562
2,0	0,47725	47,725	0,05399
2,1	0,48214	48,214	0,43398
2,2	0,48610	48,610	0,03547
2,3	0,48928	48,928	0,02833
2,4	0,49180	49,180	0,02239
2,5	0,49379	49,379	0,01753
2,6	0,49534	49,534	0,01358
2,7	0,49653	49,653	0,01042
2,8	0,49744	49,744	0,00792
2,9	0,49813	49,813	0,00595
3,0	0,49865	49,865	0,00443
3,5	0,49977	49,977	0,00087
3,99	0,49997	49,997	0,00014

Доли трансгрессирующих частот первого ряда определяются с помощью следующих выражений: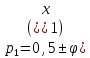

где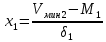

0,5 –доля половинной площади кривой первого ряда;

φ(х₁) - вторая функция нормированного отклонения первого ряда;

Vмин₂ –минимальный вариант второго ряда: Vмин₂ = М₂ – 3δ₂;

М₁ – средняя арифметическая первого ряда;

δ₁ – среднее квадратичное отклонение первого ряда.

Доля трансгрессирующих частот второго ряда определяется по аналогичной формуле, только соответственно меняются значки: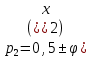

где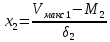

Определение разности D между средними арифметическими каждого ряда определяется по формуле:

D= М₁ – М₂

Если разность будет достоверна (когда статистическая ошибка этой разницы укладывается в ней не менее 3 раз), то такое различие между средними арифметическими обоих рядов будет свидетельствовать о трансгрессивном типе взаимоотношений между рядами.

Для определения статистической ошибки разности между средними арифметическими обоих рядов используется формула: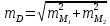

m_М1 и m_М2 - ошибки средних арифметических каждого ряда
Формулы ошибок: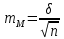

Для определения принадлежности особи (V_A) к тому или иному ряду, образующих трангрессию, пользуются методом комбинированных признаков, который основан на сопоставлении суммы квадратов отклонений, (V-M)²вычисленных для трансгрессирующих рядов.

Для решения этого вопроса используют несколько признаков, которые мало коррелируют друг с другом, но могут служить характеристикой для данных популяций.

Образец

Использование метода комбинированных признаков

Признаки	Отклонения показателей признака от средних значений вариационных рядов
1 признак	V_A-M₁	V_A-M₂
2 признак	V_A-M₁	V_A-M₂
3 признак	V_A-M₁	V_A-M₂
Квадраты отклонений по каждому признаку	1 признака (V_A-M₁)² 2 признака (V_A-M₁)² 3 признака (V_A-M₁)²	1 признака (V_A-M₂)² 2 признака (V_A-M₂)² 3 признака (V_A-M₂)²
Сумма квадратов отклонений	∑(V_A-M₁)² по трем признакам	(V_A-M₂)² по трем признакам

Особь (V_A) относится к тому или ряду, для которого сравниваемые признаки (сумма квадратов отклонений) находятся ближе (меньше).

Вариант 0:

Определить:

1.Степень трансгрессии двух вариационных рядов, характеризующих полную длину тела байкальского омуля селенгинской и северобайкальской рас возраста 7+ (мм).

Селенгинская раса: 331; 338; 327; 329; 302; 313; 270; 267; 304; 322; 312; 305; 277; 269; 335; 320; 278; 284; 328; 265; 314; 333; 321; 318; 313; 299; 287; 296; 278; 330; 281; 280.

Северобайкальская раса: 268; 261; 299, 304; 307; 277; 270; 283; 264; 255; 312; 306; 278; 265; 263; 273; 288; 281; 301; 270; 369; 260; 256; 280; 294; 290; 303; 305; 285; 282; 265; 274.

2. Достоверность разности между средними арифметическими каждого ряда

3. К какому из рядов следует отнести особь омуля с полной длиной тела 304 мм, длиной головы - 44 мм, длиной хвостового плавника - 39 мм (среднее размеры длины головы омуля селенгинской расы – 40 мм, северобайкальской – 52 мм; среднее размеры длины хвостового плавника омуля селенгинской расы – 42 мм, северобайкальской – 37 мм)
Вариант 1:

Определить:

1.Степень трансгрессии двух вариационных рядов, характеризующих массу тела двухлеток русского осетра выращенных в моно- и поликультуре (г).

Монокультура: 315; 599; 172; 266; 202; 315; 671; 380; 210; 213; 528; 270; 180; 208; 386; 101; 137; 243; 279; 189; 195; 205; 350; 326; 421; 564; 538; 140; 234; 166; 189; 195; 206.

Поликультура: 186; 136; 388; 86; 187; 287; 457; 243; 238; 628; 190; 202; 105; 337; 339; 487; 160; 365; 255; 195; 198; 275; 253; 181; 588; 164; 181; 198; 233; 269; 250; 184; 276.

2. Достоверность разности между средними арифметическими каждого ряда

3. К какому из рядов следует отнести особь осетра массой 195 г, полной длиной тела - 35,6 см, длиной тела по Смитту - 27,7 см (среднее размеры полной длины тела осетров двухлеток, выращенных в монокультуре – 42,5 см, в поликультуре – 41,2 см; среднее размеры длины тела по Смитту осетров двухлеток, выращенных в монокультуре – 32,7 см, в поликультуре – 32,3 мм)

1 2 3 4 5 6 7