Документ Microsoft Word. A AB это все три прибора, которые входят и отдельновАи отдельно в Б
 Скачать 70.12 Kb. Скачать 70.12 Kb.
|
|
1.16. События А - хотя бы один из трех проверяемых приборов бракованный, В - все приборы доброкачественные. Что означают события А+В, А·В. a) A+B - это все три прибора, которые входят и отдельно в А и отдельно в Б; б) AB - это только доброкачественные приборы. 2.16. Найти вероятность того, что при шести бросаниях игральной кости появятся все грани. 1*5/6*4/6*3/6*2/6*1/6=120/6*6*6*6*6*6=10/1296 2.46. В группе из 30 учеников на контрольной работе 6 учеников получили оценку отлично, 10 - оценку хорошо, 9 учеников - оценку удовлетворительно, 5 учеников - оценку неудовлетворительно. Какова вероятность того, что три ученика, вызванные к доске, имеют неудовлетворительную оценку по контрольной работе? Количество учеников, получивших неудовлетворительную оценку: 30 - 6 - 10 - 9 = 5; Вероятность того, что первый вызванный ученик имеет 2 по контрольной работе: p1 = 5/30; Условная вероятность того, что второй ученик тоже имеет 2, если первый имел двойку: p2 = 4/29; Условная вероятность того, что третий вызванный ученик имеет 2, если первый и второй имели двойки: p3 = 3/28; По теореме умножения вероятность того, что все три ученика, вызванные к доске имеют неудовлетворительную оценку по контрольной работе: P(3) = p1 · p2 · p3 = 5/30 · 4/29 · 3/28 = 1/406 = 0,0025; Ответ: 0,0025. 3.16. Два лица поочередно бросают монету, выигрывает тот, у кого раньше появится герб. Определить вероятность выигрыша для каждого лица. 3.46. Вероятность того, что событие А появится хотя бы один раз при двух независимых испытаниях, равна 0,75. Найти вероятность появления события в одном испытании (предполагается, что вероятность появления события в обоих испытаниях одна и та же). 4.16. При разрыве снаряда образуется 10 % крупных осколков, 60 % средних и 30 % мелких. Вероятность пробивания брони крупным осколком равна 0,7, средним - 0,2 и мелким - 0,05. Известно, что в броню попал один осколок. Определить вероятность того, что броня пробита. 4.46. В двух ящиках лежат однотипные детали: в первом ящике 8 исправных и 2 бракованные, во втором - 6 исправных и 4 бракованные. Из первого ящика наудачу взяты 2 детали, а из второго - 1 деталь. Детали, перемешав, поместили в третий ящик, откуда наугад взяли одну деталь. Определить вероятность того, что эта деталь исправна. 5.16. Телеграфная станция принимает цифровой текст. В силу наличия помех вероятность ошибочного приема любой цифры не изменяется в течение всего приема и равна 0,01. Считая приемы отдельных цифр независимыми событиями, найти вероятность того, что в тексте, содержащем 1100 цифр: а) будет ровно 7 ошибок; б) число неверно принятых цифр будет меньше 20. Ответ: Р(А) ≈ 0,9964; Р(В) ≈ 0,0176. 5.46. При штамповке металлических клемм получается в среднем 90 % годных. Найти вероятность наличия от 790 до 820 (включительно) годных в партии из 900 клемм. При штамповке металлических клемм получается в среднем 90% стандартных. Определите: а) наивероятнейшее число и вероятность наивероятнейшего числа стандартных клемм в партии из 900 клемм; б) вероятность наличия от 790 до 820 годных клемм в этой партии. Дано: p = 0,90 k1 = 790 k2 = 820 n = 900 Найти: 1) 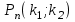 = ? 2) k0 = ? 3) = ? 2) k0 = ? 3)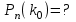 Решение: 1. Вероятность того, что клемма, полученная при штамповке, будет нестандартной, определяется как q = 1 – p = 0,1. Общее число клемм в партии составляет n, следовательно, можно говорить о n независимых испытаний, в каждом из которых вероятность того, что клемма будет признана стандартной, составляет p. Тогда в соответствии с интегральной теоремой Лапласа вероятность того, что в n независимых испытаниях, в каждом из которых вероятность появления события равна р, событие наступит не менее k1 раз и не более k2 раз, приближенно равна 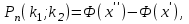 где 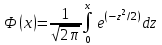 – функция Лапласа, – функция Лапласа, 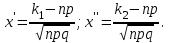 В нашем случае: 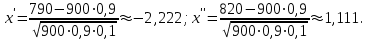 Используя табулированные значения функции Лапласа, получаем 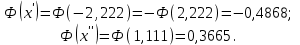 Следовательно, 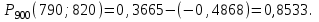 2. Наивероятнейшее число k0 стандартных клемм высчитывается из следующего неравенства: 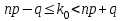 , ,где в нашем случае n = 900; p = 0,9; q = 0,1: 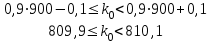 Учитывая, что k0 – целое число, k0 = 810. 3. Поскольку k0 велико, вероятность наивероятнейшего числа попаданий высчитывается при помощи локальной теоремы Лапласа: 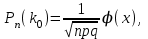 где 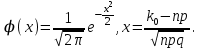 Подставляя исходные данные, вычисляем аргумент функции Лапласа 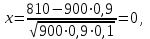 далее воспользуемся табличным значением функции φ(x): 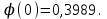 Тогда 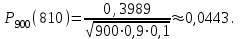 Ответ: 1) 0,8533; 2) 810; 3) 0,0443. 6.16. Вычислительное устройство состоит из трех независимо функционирующих блоков. Вероятность безотказной работы первого блока равняется 0,8, второго 0,7 и третьего 0,6. Найти математические ожидания: а) числа исправных блоков; б) числа неисправных блоков.  8.16. Автомашина проходит технический осмотр и обслуживание. Число неисправностей, обнаруженных во время техосмотра, распределяется по закону Пуассона с параметром "а". Если неисправностей не обнаружено, техническое 60 обслуживание машины продолжается в среднем 2 ч. Если обнаружены одна или две неисправности, то на устранение каждой из них тратится в среднем еще полчаса. Если обнаружено больше двух неисправностей, то машина ставится на профилактический ремонт, где она находится в среднем 4 ч. Определить закон распределения среднего времени обслуживания и ремонта машины и его математическое ожидание М[Т]. 9.16. Случайная величина X подчинена нормальному закону с параметрами а, σ. Вычислить с точностью до 0,01 вероятность попадания значений случайной величины X в интервал (а; а+σ) (без использования таблиц функции Лапласа). 10.16. Имеется система случайных величин (X,Y), где m ,0 m ,2 D ,2 D 1 x = y = x = y = и коэффициент корреляции 2 1 rxy = − . Найти математическое ожидание и дисперсию случайной величины Z = 2X − 3Y. 11.16. Плотность совместного распределения системы случайных величин X, Y равна 2 )1y( 8 )3x( 2 2 )y,x(f ae − − + − = . Найти коэффициент a. Установить, являются ли величины зависимыми. Определить вероятность совместного выполнения двух неравенств x < -3; y < 4. |
