контрольная. УП Сироткин, Семенова, Козлова исправленная пос.. (4). А., Козлова Ю. А. Методы и инструменты финансовоэкономических расчетов

• Название: А., Козлова Ю. А. Методы и инструменты финансовоэкономических расчетов
• Анкор: контрольная
• Дата: 11.04.2022
• Размер: 1.6 Mb.
• Имя файла: УП Сироткин, Семенова, Козлова исправленная пос.. (4).doc
• Тип: Учебное пособие; #462117
• страница: 8 из 16

Консолидация и изменение условий платежей

Изменение хозяйственной ситуации часто приводит к тому, что одна из сторон – участниц коммерческой сделки обращается к другой стороне с предложением изменить условия ранее заключенных соглашений. Среди таких предложений могут быть: изменение сроков платежей в сторону увеличения, разбивка одного платежа на несколько с разными сроками погашения (погашение частями) и т.п. Наиболее распространенным вариантом является объединение платежей в один (консолидация платежей) с установлением единого срока погашений. Основным принципом изменения условия сделки является принцип финансовой тождественности (эквивалентности), т.к. предлагаемые изменения должны быть безубыточными для обеих сторон. В соответствии с этим принципом платежи могут считаться тождественными в том случае, если они оказываются равными при приведении к одной дате.

Для решения задач такого типа используется уравнение тождественности, в котором сумма заменяемых платежей, приведенных к одному моменту времени, приравнена к сумме платежей по новому соглашению, приведенной к той же дате.

При консолидации нескольких платежей в один при условии, что срок нового платежа больше сроков каждого из первоначальных сроков, уравнение тождественности имеет вид:

• 
  для простых процентов
  
• 
  для сложных процентов ,
  

где S₀ – наращенная сумма консолидированного платежа;

S₁, S₂, … S_j – платежи, подлежащие консолидации, со сроками уплаты n₁, n₂, … n_j, n_k;

n₀ – срок консолидации;

t_j – временные интервалы между сроком консолидированного платежа n₀ и сроками платежей, подлежащих консолидации, n_j, т.е. n₀ >n_{j ,}t_j = n₀ - n_j;

t_k – временные интервалы между сроками платежей, подлежащих консолидации, n_k и сроком консолидированного платежа n₀, т.е. n₀ <n_{k ,}t_k = n_k – n₀;

Если срок консолидированного платежа оказывается меньше срока одного из сроков платежей первоначального соглашения, то приведение суммы этого платежа к необходимой дате осуществляется посредствам не наращения, а дисконтирования. В этом случае величину консолидированного платежа определяют по формуле:

• 
  для простых процентов
  

;

• 
  для сложных процентов
  

где S_j – суммы объединенных платежей, сроки погашения которых меньше нового срока;

S_k – суммы объединенных платежей со сроками погашения, превышающими новый срок.

При консолидации векселей в расчетах используется учетная ставка. Если срок консолидированного векселя меньше срока одного из сроков первоначальных векселей, то расчет конечной суммы производится по формуле:

• 
  для простой учетной ставки
  

;

• 
  для сложной учетной ставки
  

.

Сроки консолидированного платежа определяют по формуле:

• 
  для простых процентов
  

;

• 
  для сложных процентов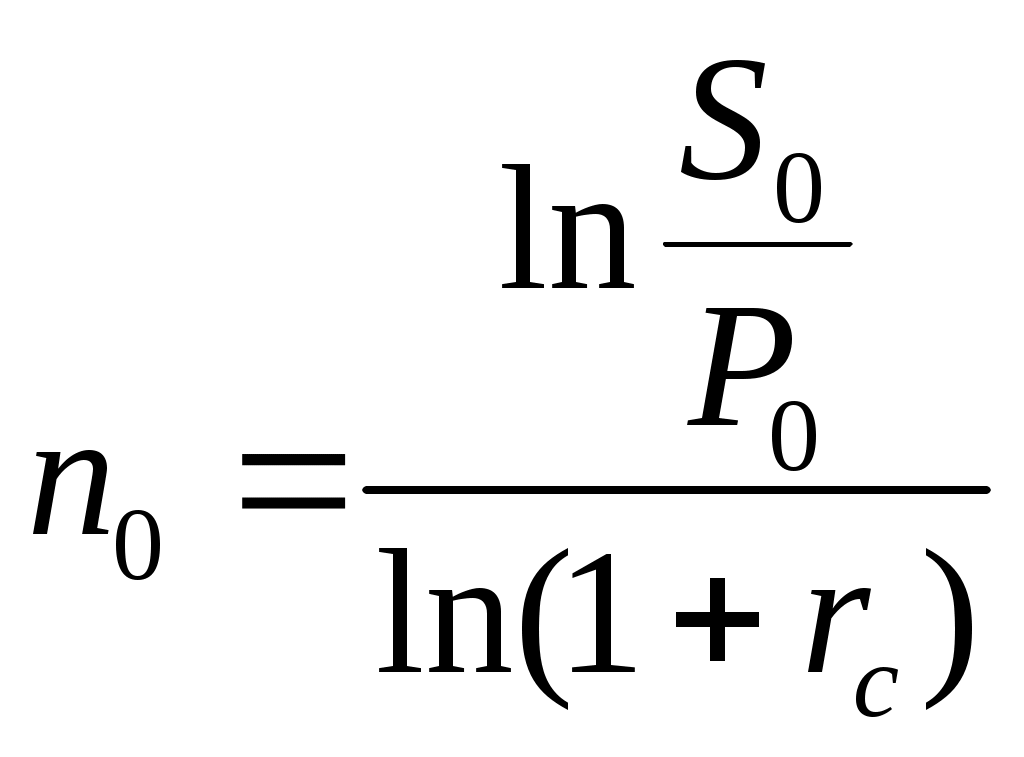
  

;

• 
  для простой учетной ставки
  

;

• 
  для сложной учетной ставки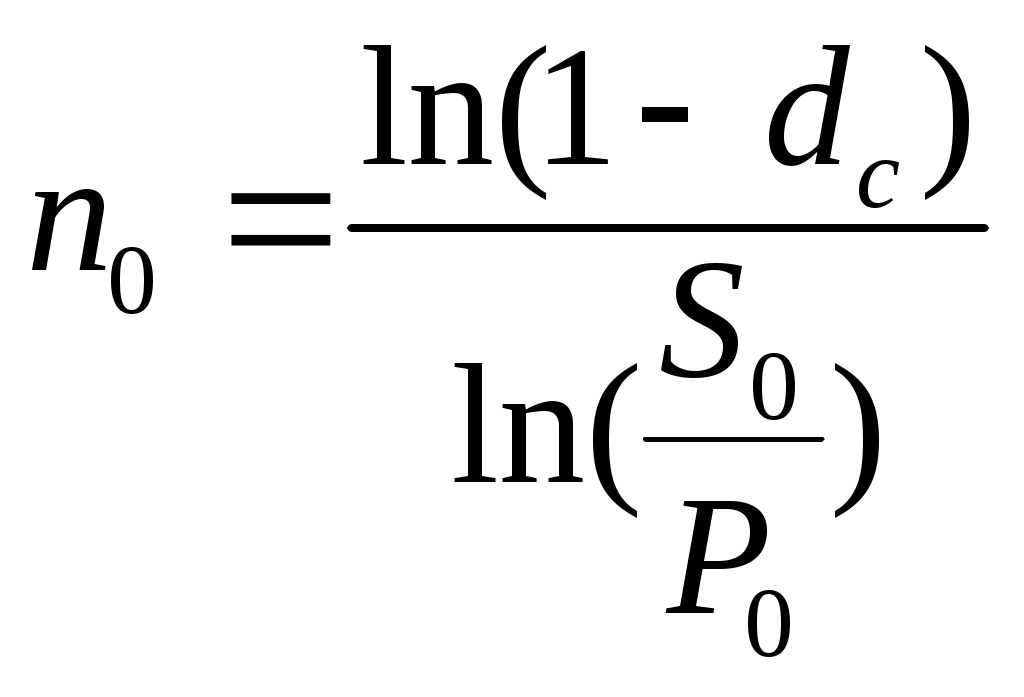
  

.

При изменении условий коммерческих сделок далеко не всегда можно найти решение путем суммирования наращенных сумм и дисконтированных платежей. Зачастую для решения этой задачи готовые формулы отсутствуют.

Расчет исходной величины S₀ , отражающей результат изменения условий сделки, можно выполнить, используя принцип эквивалентности и его математическое выражение – уравнение эквивалентности. Его экономический смысл был рассмотрен нами выше. За момент приведения платежей могут быть при этом приняты различные даты: начальная дата, т.е. дата предоставления кредита, дата, находящаяся в конце срока, в середине и т.д. Конкретный вид уравнения зависит от условий контрактов.

Рассмотрим примеры использования уравнения тождественности.


Пример 1.

Организация получила кредит на сумму 1 млн. руб. под 20% годовых (простые проценты). Кредит должен был быть погашен двумя платежами: первый – 400 тыс. руб. с процентами через 120 дней, а второй – 600 тыс.руб. с процентами через 150 дней. Впоследствии фирма договорилась об объединении платежей в один со сроком погашения через 180 дней. Определить размер консолидированного платежа (К = 360 дней).

Решение:

Суммы, подлежащие возврату на старых условиях:





Сумма погашения консолидированного платежа будет равна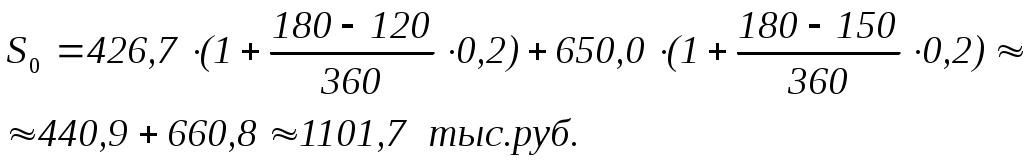



Можно проверить полученный результат. По принципу эквивалентности дисконтированная сумма консолидированного платежа на момент предоставления кредита должна быть равна сумме полученного кредита (возможна небольшая погрешность за счет округления):



С учетом погрешности, возникшей при округлении, можно сделать вывод, что расчет произведен верно.

Пример 2.

Два платежа 1,7 млн.руб. и 1,3 млн.руб. со сроками погашения 1 год 30 дней и 1 год 45 дней, отсчитываемыми от одной даты, заменяются одним платежом со сроком 1 год 75 дней. Стороны согласились на консолидацию платежей при использовании ставки сложных процентов 9% годовых. Определить сумму консолидированного платежа.

Решение:





Таким образом сумма консолидированного платежа равна 3,027 млн.руб.

Пример 3.

Имеются два кредитных обязательства – 500 тыс. руб. и 600 тыс. руб. со сроками уплаты 01.10 и 01.01 (нового года). По согласованию сторон обязательства были пересмотрены на новые условия: первый платеж в размере 700 тыс. руб. должник вносит 01.02, остальной долг он выплачивает 01.04. При расчетах используется простая процентная ставка – 10% годовых. Необходимо определить величину второго платежа.

Решение.

За базовую дату, т.е. дату приведения, примем 01.01 (нового года).

01.10 – 274-й порядковый день в году;

01.02 – 32-й день;

01.04 – 91-й день.

Запишем уравнение эквивалентности: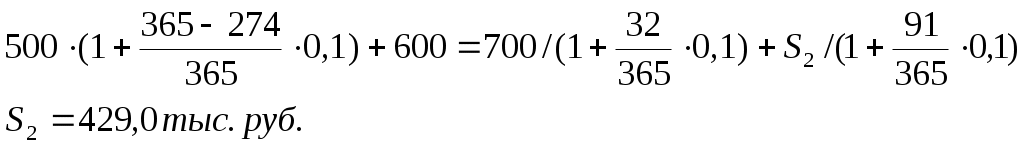


Задачи для самостоятельного решения.

Задача 1. Фирма в погашение задолженности банку за предоставленный под 15% годовых (простые проценты) кредит, полученный 01.01, должна произвести три платежа – 250 тыс.руб., 300 тыс.руб. и 350 тыс.руб. в срок 20.04, 25.05, 15.06. Фирма предложила банку объединить все платежи в один и погасить его 01.06. Определить величину консолидированного платежа.

Задача 2. По первоначальным условиям долг необходимо было погасить тремя платежами 400 тыс.руб. (15.03), 750 тыс.руб. (10.04) и 800 (01.06). По новым условиям платежи объединяются в один со сроком погашения 15.05. При консолидации используется процентная ставка 9% годовых. Определить величину консолидированного платежа.

Задача 3. Фирма имеет ряд финансовых обязательств перед одним кредитором – 2,5 млн.руб., 3,1 млн.руб. и 2,7 млн.руб., которые должна погасить через 40, 70 и 160 дней после 01.01 текущего года. По согласованию сторон решено заменить их одним платежом, равным 9 млн.руб., с продлением срока уплаты, используя процентную ставку 12% годовых. Определить срок уплаты консолидированного платежа.

Задача 4. Должник обратился к своему кредитору (владельцу векселей) с просьбой объединения двух векселей в один с одновременным продлением срока оплаты. Первый вексель выдан на сумму 200 тыс.руб. со сроком уплаты 31.03; второй – на сумму 250 тыс.руб. со сроком уплаты 01.06. Владелец векселей согласился на пролонгацию до 01.10, применив простую учетную ставку 10%.