Высшая математика 2. Абсциссами точек перегиба графика функции являются

• Название: Абсциссами точек перегиба графика функции являются
• Дата: 03.03.2023
• Размер: 1.3 Mb.
• Имя файла: Высшая математика 2.doc
• Тип: Документы; #967392
• страница: 2 из 6

38. 
    
    

Достаточными условиями существования производной непрерывной функции в точке являются:

Существование и равенство двух односторонних производных

Существование хотя бы одной односторонней производной

Существование двух односторонних производных

39. 
    
    

Заменив приращение функции дифференциалом, приближенно найти arctg 1,05.

0,81

0,69

0,75

0,65

0,80

40. 
    
    

Заменив приращение функции дифференциалом, приближенно найти sin 31º.

0,500

0,491

0,451

0,35

0,515

41. 
    
    

Из непрерывности функции

следует непрерывность первой производной

еще не следует ее дифференцируемость

следует ее дифференцируемость

следует разрывность первой производной

42. 
    
    

Используя свойства определителя, вычислить определитель:

6

1

4

2

0

43. 
    
    

Используя свойства определителя, вычислить определитель:

-7

2

0

4

6

44. 
    
    

Используя свойства определителя, вычислить определитель: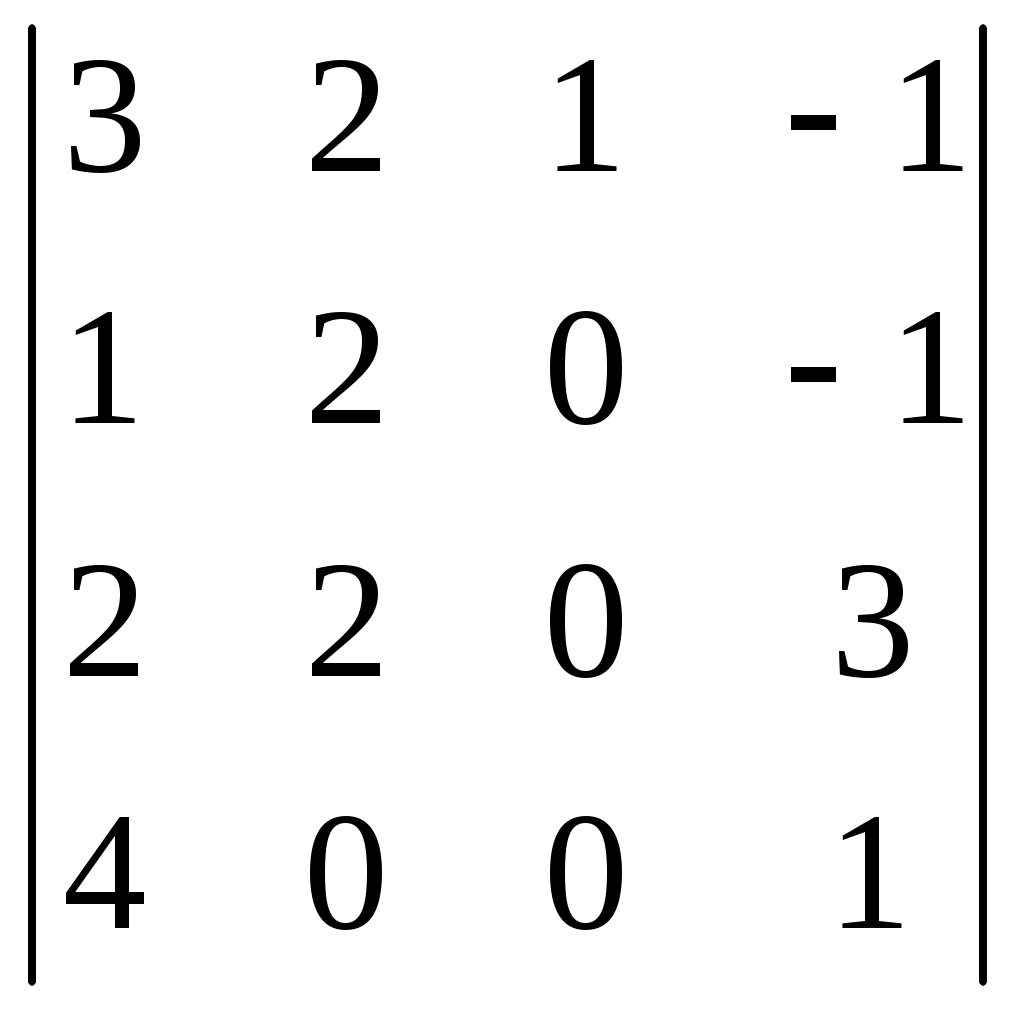

40

30

10

50

20

45. 
    
    

Используя свойства определителя, вычислить определитель: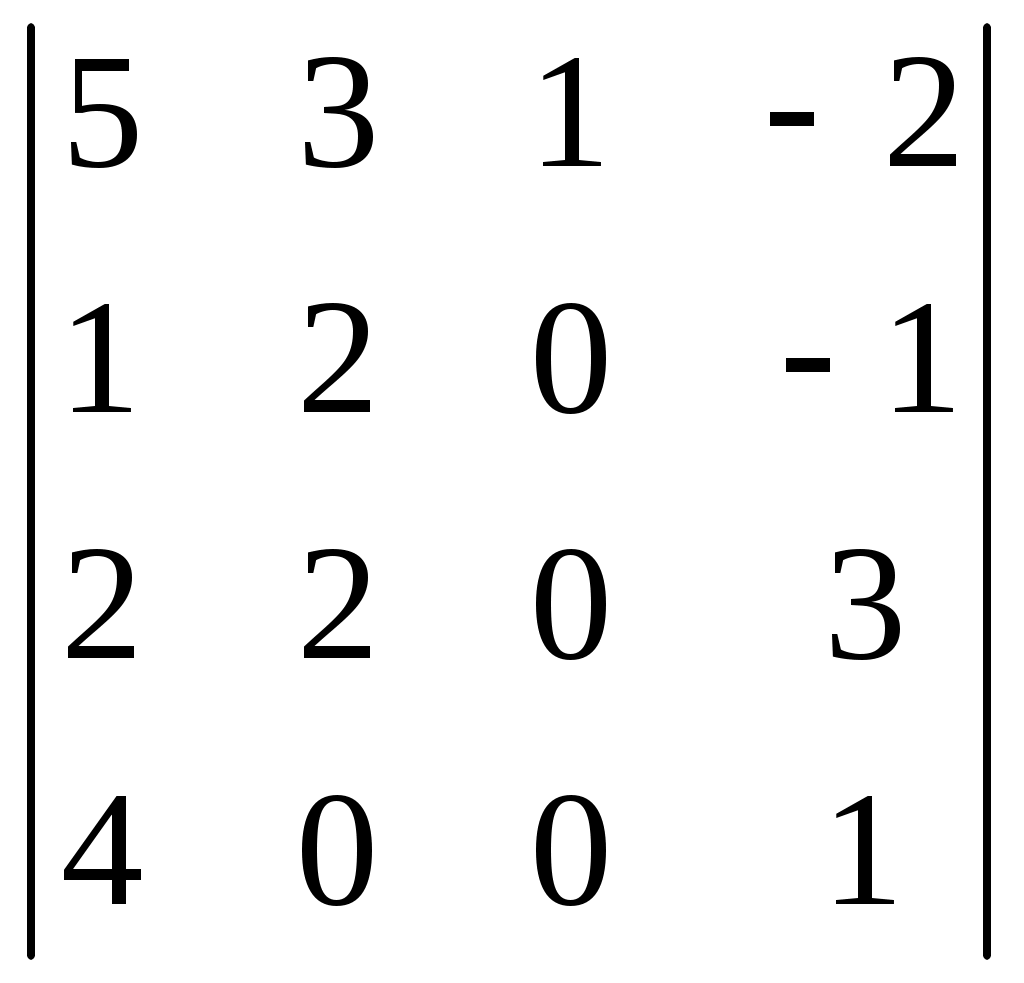

30

20

50

10

40

46. 
    
    

Какая из заданных функций задана явно:

;

у = sinx;

lg(x + y) = 5.

ху = 5;

;

47. 
    
    

Какая из заданных функций является обратной для функции Y = 5x – 3:

;

;

;

.

;

48. 
    
    

Какая из заданных функций является четной:

у = х.

;

;

;

у = х + 2;

49. 
    
    

Касательная к графику функции в точке определяется уравнением

у = х –1

у = 2х – 1

у = 2х + 3

у = 2х + 1

у = х + 1

50. 
    
    

Наибольшим значением функции на отрезке [–1; 1] является:

5

10

3

-1

∞

51. 
    
    

Найдите вторую производную заданной функции

52. 
    
    

Найдите вторую производную функции .

53. 
    
    

Найти все точки разрыва функции

2 и 6



1 и 4

3 и 5

1 и 2

54. 
    
    

Найти интеграл

55. 
    
    

Найти интеграл

56. 
    
    

Найти интеграл

57. 
    
    

Найти интеграл

58. 
    
    

Найти интеграл

59. 
    
    

Найти интеграл

60. 
    
    

Найти интеграл

61. 
    
    

Найти интеграл

62. 
    
    

Найти интеграл

63. 
    
    

Найти интеграл

64. 
    
    

Найти интеграл

65. 
    
    

Найти интеграл

66. 
    
    

Найти интеграл

67.