МАТЕМАТИКА. Вопросы для экзамена Частные производные. Дифференцируемость. Полный дифференциал

Название	Вопросы для экзамена Частные производные. Дифференцируемость. Полный дифференциал
Дата	19.09.2022
Размер	3.63 Mb.
Формат файла
Имя файла	МАТЕМАТИКА.docx
Тип	Вопросы для экзамена #684943

Вопросы для экзамена

Частные производные. Дифференцируемость. Полный дифференциал

Частная производная — это предел отношения приращения функции по выбранной переменной к приращению этой переменной, при стремлении этого приращения к нулю.

Дифферинцируемость: если в функции от одной переменной то говорит о наличии в ней производной,

Если в функции от нескольких переменных то это будет необходимое (но не достаточное) условие частного производного

Полный дифференциал равен сумме попарных произведений частных производных на дифференциалы соответствующих переменных. ... В левой части получим частное приращение функции по переменной x.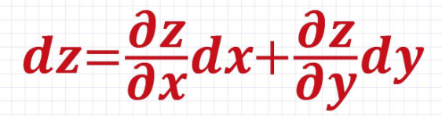

2. Производная сложной функции. Полная производная.

сначала берется производная внутренней функции, далее от внешней.

Полная производная функции — производная функции по времени вдоль траектории.

3. Производная неявной функции.

Если функция задана уравнением у = f(x) , разрешенным относительно (у), то говорят, что функция задана в явном виде. Под неявным заданием функции понимают задание функции в виде уравнения не разрешенного относительно у: F(x; y) = 0 Для нахождения производной неявно заданной функции необходимо продифференцировать уравнение по х, рассматривая при этом у как функцию от х, и полученное выражение разрешить относительно производной.

4. Производная по направлению. Градиент скалярной функции.

Производная по направлению показывает, как быстро значение функции изменяется при движении в данном направлении.

Производная функции одной переменной показывает, как изменяется её значение при малом изменении аргумента. Если мы попытаемся по аналогии определить производную функции многих переменных, то столкнёмся с трудностью: в этом случае изменение аргумента (то есть точки в пространстве) может происходить в разных направлениях, и при этом будут получаться разные значения производной. Именно это соображение и приводит к определению производной по направлению

Градиент скалярной величины – векторная величина, численно равная производной от этой функции по направлению нормалей к поверхности уровня.

Смысл градиента любой скалярной функции в том, что его скалярное произведение с бесконечно малым вектором перемещения дает полный дифференциал этой функции при соответствующем изменении координат в пространстве, на котором определена, то есть линейную (в случае общего положения она же главная) часть изменения при смещении на. Применяя одну и ту же букву для обозначения функции от вектора и соответствующей функции от его координат, можно написать: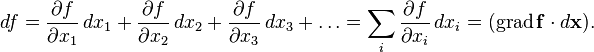

5. Касательная плоскость и нормаль к поверхности.

Касательная плоскость к поверхности в точке – это плоскость, содержащая касательные ко всем кривым, которые принадлежат данной поверхности и проходят через точку М₀

если поверхность задана уравнением

(т.е. неявно), то уравнение касательной плоскости к данной поверхности в точке

можно найти по следующей формуле:

6. Экстремум функции нескольких переменных. Необходимое и достаточное

условие экстремума

7. Двойной интеграл: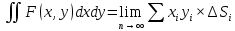

Где: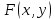

нез. Интегрируемая функция в области D

D – область интегрирования

x,y – переменные интегрирования

Свойства двойного интеграла:

1) Константу «С» можно вынести за знак интеграла

2) сумму и разность функций которые находятся под одним интегралом можно представить в виде суммы или разности двух интегралов

3) Если D задана как пересечение двух областей, то D=D₁ U D₂

То интеграл этой области можно разбить на сумму или разность интеграла первой области и второго соответственно.

Вычисление двойного интеграла в декартовых координатах

Чтобы вычислить двойной интеграл, надо проинтегрировать f(x,y) по у, считая х – фиксированным, в пределах от точки входа до точки выхода, а затем полученный результат проинтегрировать по х в пределах его наибольшего изменения. Следовательно, для вычисления двойного интеграла нужно произвести последовательное вычисление двух обычных определенных интегралов.

8. Построение криволинейного интеграла I рода.

Теорема о существовании криволинейного интеграла 1 рода

Вычисление криволинейного интеграла 1 рода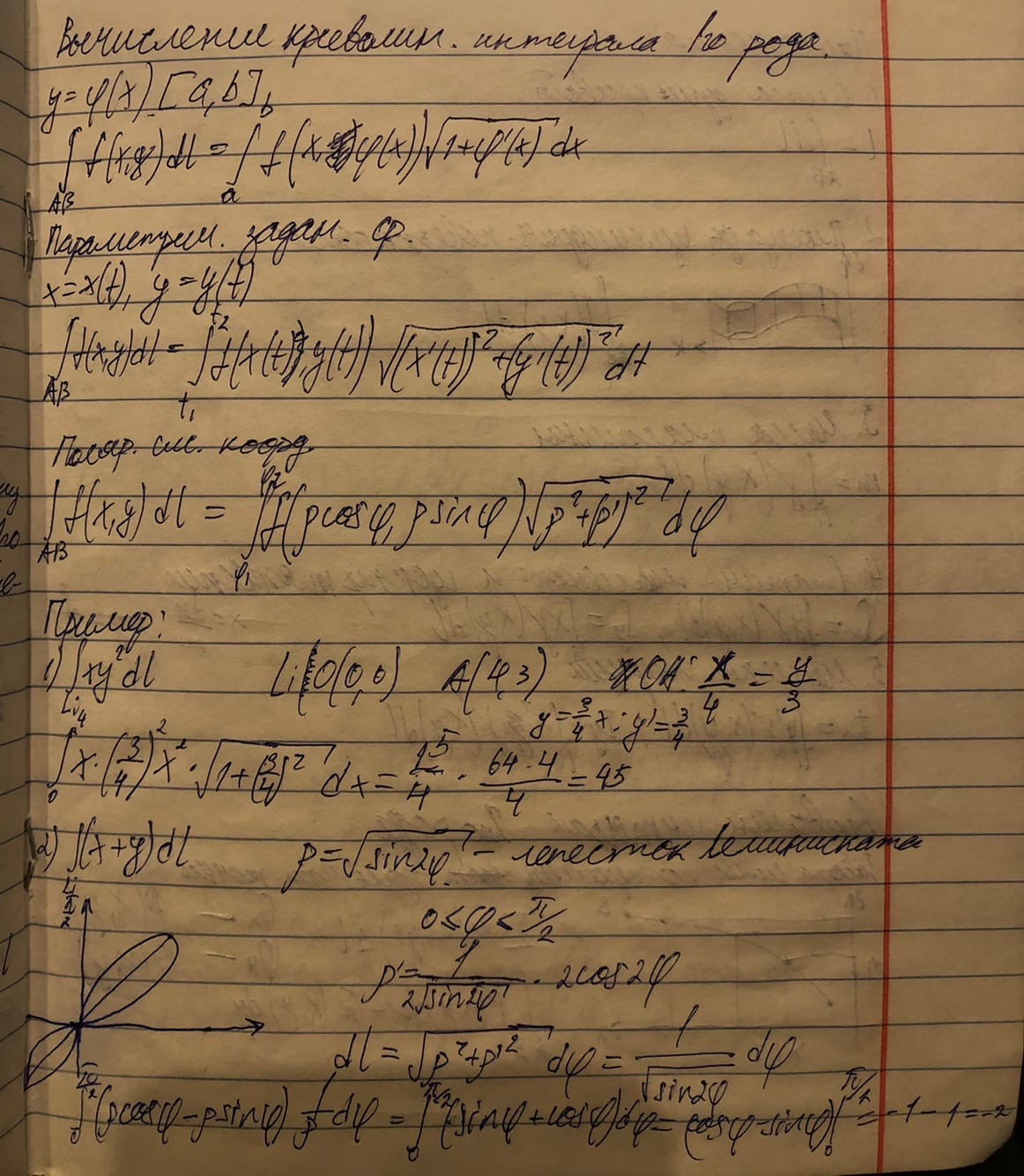

Приложения криволинейного интеграла 1 рода

9. Криволинейный интеграл 2го рода показывает работу силы материальной точки – главное приложение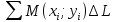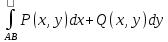

Свойства криволинейного интеграла 2го рода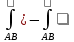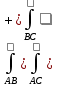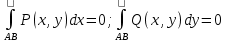

Криволинейный интеграл по замкнутой кривой не зависит от выбора начальной точки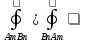

10. Интеграл по замкнутому контуру. Формула Грина.

11. Поверхностный интеграл

Поверхностный интеграл 2го рода

Связь между поверхностными интегралами 1го и 2го рода

12. ) Векторное и скалярное поле

Векторное и скалярное поле

Градиент— вектор, своим направлением указывающий направление наибольшего возрастания некоторой величины φ, значение которой меняется от одной точки пространства к другой (скалярного поля), а по величине (модулю) равный скорости роста этой величины в этом направлении.

Дивергенция — дифференциальный оператор, отображающий векторное поле на скалярное, который определяет для каждой точки, «насколько расходится входящее и исходящее из малой окрестности данной точки поле», точнее, насколько расходятся входящий и исходящий потоки.

Ротор {\displaystyle \operatorname {rot} \,\mathbf {a} } векторного поля {\displaystyle \mathbf {a} } — есть вектор, проекция которого {\displaystyle \operatorname {rot} _{\mathbf {n} }\mathbf {a} } на каждое направление n есть предел отношения циркуляции векторного поля по контуру L, являющемуся краем плоской площадки ΔS, перпендикулярной этому направлению, к величине этой площадки (площади), когда размеры площадки стремятся к нулю, а сама площадка стягивается в точку

Потоком векторного поля

,

через поверхность S называется поверхностный интеграл второго рода от векторной функции A (x, y, z) по поверхности S,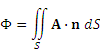

,

где n – единичный вектор внешней нормали к поверхности S.

13. Поток через замкнутую поверхность. Формула Остроградского-Гаусса.

Формула Остроградского-Гаусса означает, что поток векторного поля через замкнутую поверхность

(в направлении внешней нормали, т. е. изнутри) равен тройному интегралу от дивергенции этого поля по объему

, ограниченному данной поверхностью.

a*ds=divadV

14. Преобразование Лапласа

Преобразование Лапласа — интегральное преобразование, связывающее функцию изображение с функцией оригинала. С его помощью исследуются свойства динамических систем и решаются дифференциальные и интегральные уравнения.

f(t) -> F(p)

Решение задачи Коши для линейных ДУ

Решение задачи Коши не содержит произвольной константы C. Ее конкретное числовое значение определяется подстановкой общего решения уравнения в заданное начальное условие

состоит в нахождении решения (интеграла) дифференциального уравнения, удовлетворяющего так называемым начальным условиям (начальным данным).

15. Классическое определение вероятности события

16. Формулы полной вероятности, формула Байеса переоценки гипотез

Если событие А может произойти только при выполнении одного из событий

, которые образуют полную группу несовместных событий, то вероятность события А вычисляется по формуле

.

Эта формула называется формулой полной вероятности.

Вновь рассмотрим полную группу несовместных событий

, вероятности появления которых

. Событие А может произойти только вместе с каким-либо из событий

, которые будем называть гипотезами. Тогда по формуле полной вероятности

Если событие А произошло, то это может изменить вероятности гипотез

.

По теореме умножения вероятностей

,

откуда

.

Аналогично, для остальных гипотез

Полученная формула называется формулой Байеса (формулой Бейеса). Вероятности гипотез

называются апостериорными вероятностями, тогда как

- априорными вероятностями.

Формула байеса

17. Повторные независимые испытания. Формула Бернулли. Теоремы Лапласа.

Формула Бернулли — формула в теории вероятностей, позволяющая находить вероятность появления события A{\displaystyle A} определённое количество раз при любом числе независимых испытаний. Формула Бернулли позволяет избавиться от большого числа вычислений — сложения и умножения вероятностей — при достаточно большом количестве испытаний. Названа в честь выдающегося швейцарского математика Якоба Бернулли, который вывел эту формулу.

18. Случайные величины

Случайная величина — это математическое понятие, служащее для представления случайных явлений, когда для них может быть определена их вероятность, то есть мера возможности наступления

Законом распределения дискретной случайной величины называется любое правило, позволяющее находить вероятности всевозможных событий, связанных со случайной.

Самыми важными числовыми характеристиками случайной величины являются ее математическое ожидание, имеющее смысл среднего значения, и дисперсия, характеризующая разброс значений случайной величины относительно ее математического ожидания. (мат ожидание, Дисперсия, Среднеквадратическое отклонение, Мода, Медиана, Срединное (вероятное) отклонение, Корреляционный момент, Коэффициент корреляции)

Функция распределения

19. Непрерывные СВ

Непрерывной случайной величиной называют случайную величину, которая в результате испытания принимает все значения из некоторого числового промежутка. Число возможных значений непрерывной случайной величины бесконечно.

Функция ПЛОТНОСТИ распределения вероятностей или дифференциальная функция распределения. Она представляет собой производную функции распределения:

– равен единице, и строго единице. В противном случае перед нами не функция плотности, и если эта функция была найдена как производная, то

– не является функцией распределения (несмотря на какие бы то ни было другие признаки)

Рассмотрим общие свойства функций распределения.

Свойство 1. Функция распределения есть неотрицательная функция, заключенная между нулем и единицей:

.

Справедливость этого свойства вытекает из того, что функция распределения

определена как вероятность случайного события, состоящего в том, что

.

Свойство 2. Вероятность попадания случайной величины в интервал равна разности значений функции распределения на концах этого интервала, т. е.

.

Отсюда следует, что вероятность любого отдельного значения непрерывной случайной величины равна нулю.

Свойство 3. Функция распределения случайной величины есть неубывающая функция, т. е. при

.

Свойство 4. На минус бесконечности функция распределения рана нулю, а на плюс бесконечности функция распределения рана единице, т. е. , .

Законом распределения СВ называется любое соотношение, устанавливающее связь между возможными значениями СВ и соответствующими им вероятностями. Непрерывная СВ – величина, бесконечное несчетное множество значений которой есть некоторый интервал (конечный или бесконечный) числовой оси

Нормальный закон распределения (закон Гаусса)

Плотность вероятности нормально распределённой случайной величины выражается формулой

Равномерным распределением называют такое распределение случайной величины, при котором она может принимать любое значение в заданных пределах с одинаковой вероятностью.

Показательным или экспоненциальным, называется распределение вероятностей непрерывной случайной величины X, которое описывается плотностью f(x)={0,приx<0λe−λx,приx⩾0,λ−const

и имеет один параметр λ

. В этом его преимущество перед другими распределениями.

20. ) Наблюдение двумерной СВ

Коэффициент корреляции (или линейный коэффициент корреляции) обозначается как «r» (в редких случаях как «ρ») и характеризует линейную корреляцию (то есть взаимосвязь, которая задается некоторым значением и направлением) двух или более переменных. Значение коэффициента лежит между -1 и +1, то есть корреляция бывает как положительной, так и отрицательной. Если коэффициент корреляции равен -1, имеет место идеальная отрицательная корреляция; если коэффициент корреляции равен +1, имеет место идеальная положительная корреляция. В остальных случаях между двумя переменными наблюдается положительная корреляция, отрицательная корреляция или отсутствие корреляции.

Линейная регрессия — модель зависимости переменной x от одной или нескольких других переменных (факторов, регрессоров, независимых переменных) с линейной функцией зависимости.

Математическое уравнение, которое оценивает линию простой (парной) линейной регрессии:

Y=a+bx.

x называется независимой переменной или предиктором.

Y – зависимая переменная или переменная отклика. Это значение, которое мы ожидаем для y (в среднем), если мы знаем величину x, т.е. это «предсказанное значение y»

a – свободный член (пересечение) линии оценки; это значение Y, когда x=0 (Рис.1).
b – угловой коэффициент или градиент оценённой линии; она представляет собой величину, на которую Y увеличивается в среднем, если мы увеличиваем x на одну единицу.
a и b называют коэффициентами регрессии оценённой линии, хотя этот термин часто используют только для b.

21. Статистическая выборка.

Статистическое наблюдение (Выборка). ВЫБОРОЧНОЕ НАБЛЮДЕНИЕ – вид статистического наблюдения, организованный на основе выборки, при котором отбирается часть единиц изучаемой совокупности, по определённым правилам, из общей совокупности единиц. Совокупность единиц, из которых осуществляется отбор, называется ген. совокупностью.

Выборочное среднее

Выборочной дисперсией

называется среднее арифметическое квадратов отклонений значений выборки от их выборочного среднего:

.

Модой М_о вариационного ряда называется вариант, имеющий наибольшую частоту (или относительную частоту).

Медианой М_е вариационного ряда называется число, являющееся его серединой. Для дискретного ряда с нечетным числом вариант медиана равна его серединному варианту. Если же число вариант четно, то Медина равна среднему (т.е. полусумме) двух серединных вариант.

Гистогра́мма — способ представления табличных данных в графическом виде — в виде столбчатой диаграммы. Количественные соотношения некоторого показателя представлены в виде прямоугольников, площади которых пропорциональны.

22. Статистическая гипотеза. Статистический критерий.

Статистическая гипотеза - это некоторое предположение о свойствах генеральной совокупности, которое необходимо проверить. Статистические гипотезы выдвигаются, когда необходимо проверить, является ли наблюдаемое явление элементом случайности или результатом воздействия некоторых мероприятий.

Статистический критерий - статистическая характеристика выборки, вычисляемая по некоторому математическому соотношению (формуле) на основе данных, имеющихся в выборке.

По значению этой характеристики принимается решение, принимать основную гипотезу или нет. Статистические критерии бывают двух видов:

односторонний критерий - критерий, значения которого принадлежат области (0; +∞);
двусторонний критерий - критерий, значения которого принадлежат области (-∞; +∞).

Свойства статистического критерия:

статистический критерий является случайной величиной, закон распределения которой известен. Зачастую в названии статистического критерия упоминается его закон распределения. Например, критерий хи-квадрат-Пирсона подчиняется закону распределения хи-квадрат;
чем ближе значение статистического критерия к нулю, тем более вероятно, что основная гипотеза является верной.

Шаги проверки статистических гипотез следующие:

формулируется основная гипотеза H0 и альтернативная гипотеза H1;
выбирается статистический критерий, с помощью которого будет проверяться гипотеза;
задаётся значение уровня значимости α;
находятся границы области принятия гипотезы;
делается вывод о принятии или отвержении основной гипотезы H0.