Лекция группировки. Абсолютные, относительные и средние величины
 Скачать 164.5 Kb. Скачать 164.5 Kb.
|
|
ЛЕКЦИЯ 4 АБСОЛЮТНЫЕ, ОТНОСИТЕЛЬНЫЕ И СРЕДНИЕ ВЕЛИЧИНЫ Общие принципы построения статистических показателей Экономико-статистические показатели содержат количественную характеристику тех или иных свойств экономических явлений. Показатель формализует содержание изучаемых сторон социально-экономических явлений. Чем сложнее исследуемое явление, тем труднее оно поддается формализации и моделированию. С помощью показателей определяется, что, где, когда и каким образом следует численно измерить. Каждый статистический показатель с возможной точностью должен соответствовать сущности того явления, которое должно, быть измерено с его помощью. Например, измерение объема продукции промышленности требует предварительного установления тех видов деятельности промышленного предприятия, которые будут учтены в составе промышленной продукции, и определения тех результатов этой деятельности, которые могут быть включены в ее объем. Необходимость рассмотрения исследуемого объекта во всех его связях и отношениях приводит к тому, что для получения целостной статистической характеристики изучаемых явлений применяются системы статистических показателей. Важнейшая особенность системы показателей - их содержательное единство, связанное с характеристиками единого объекта исследования. Так, система стоимостных показателей продукции промышленного предприятия включает следующие показатели: товарная продукция, отгруженная продукция, реализованная продукция, чистая продукция, стоимость, добавленная обработкой и др. Совершенствование управления экономикой обусловило переход от преимущественной ориентации на показатель валовой продукции к таким показателям, оценивающим вклад непосредственно данного предприятия в производство продукции, как стоимость, добавленная обработкой, или чистая продукция. С одной стороны, переход к количественному описанию явлений действительности обогащает и уточняет понятие о явлениях. С другой, - при построении показателей почти всегда приходится дополнительно упрощать, схематизировать реальные явления, а потому статистические показатели лишь с известной степенью приближения отражают объективную реальность. Все это делает очень важной постоянную работу по совершенствованию системы показателей. Развитие систем статистических показателей происходит в соответствии с развитием отражаемой объективной действительности и в результате углубления процесса познания реальных систем. При формировании систем статистических показателей должны быть четко сформулированы значение и область применения соответствующих показателей, определены функции, которые им надлежит выполнять. Статистические показатели - это величины, адекватно характеризующие отображаемое явление в конкретных условиях времени и места. Функции статистических показателей: - учетная; - директивная; -стимулирующая; -познавательная. В этом определении прежде всего охарактеризована учетная функция статистических показателей, реализация которой связана с отражением в них объективных свойств изучаемых явлений. Изучая отчетные данные по действующей системе показателей, руководители разного уровня управления должны получить объективную информацию о реальном состоянии и тенденциях развития организаций, отраслей и экономики в целом. Руководствуясь действующей системой показателей, планирование может сознательно направлять развитие предприятий, фирм, корпораций. Плановые показатели, осуществляя директивную функцию, призваны ориентировать руководителей и работников предприятий на выполнение поставленных задач. Составы систем плановых и учетно-статистических показателей различаются и довольно значительно, что связано с необходимостью проведения комплексного и всестороннего анализа деятельности предприятий. С помощью анализа выявляются неиспользованные резервы, определяются пути устранения отмеченных недостатков в работе и т.д. При этом нужно иметь в виду, что отчетные показатели должны быть сопоставимы с плановыми по методологии их определения. Статистические показатели призваны способствовать усилению воздействия плановых показателей на деятельность производственных коллективов, т.е. в определенной степени выполнять также стимулирующую функцию. Таким образом система экономико-статистических показателей в управлении предприятиями призвана выполнять три основные функции: директивную, учетную и стимулирующую. В практике хозяйственной деятельности некоторые из применяемых показателей выполняют одновременно все названые функции. Вместе с тем необходимо отметить, что статистические показатели не только играют важную роль в формировании информационного обеспечения управления разных уровней, но и используются в повышении информированности всего населения страны о процессах, происходящих в экономическом и социальном развитии общества. С этих позиций очень важна познавательная функция статистических показателей. Абсолютные величины В процессе статистического наблюдения получают данные о значениях тех или иных признаков, характеризующих каждую единицу исследуемой совокупности. Для характеристики совокупности в целом или отдельных ее частей данные по отдельным единицам совокупности подвергают сводке и получают обобщающие показатели, в которых отражаются результаты познания количественной стороны изучаемых явлений. Обобщающие показатели могут быть представлены абсолютными, относительными и средними величинами. Они широко используются в планировании и анализе деятельности предприятий, фирм, концернов, отраслей и экономики в целом. Многообразная характеристика всех сторон исследуемых социально-экономических явлений может быть дана лишь с помощью всех видов обобщающих показателей. Вместе с тем, каждый вид показателей имеет определенное значение и занимает различное место в процессе познания реальной действительности. Путем непосредственного суммирования первичных данных получают обобщающие абсолютные показатели, которые характеризуют численность совокупности и объем (размер) изучаемого явления в конкретных границах времени и места. Например, численность населения России в 2010 году составила 141,9 млн. человек. Абсолютные показатели являются всегда именованными числами, т.е. имеют какую-либо единицу измерения. Например, производство цемента оценивается в тоннах, тканей - в квадратных метрах, автомобилей - в штуках и т.д. Натуральные единицы могут быть и составными (сложными). Например, отработанное рабочими время учитывается в человеко-днях и человеко-часах, грузооборот автомобильного и железнодорожного транспорта - в тонно-километрах и т.п. Составные единицы отражают сочетание двух различных сторон явления. При учете продукции в натуральном выражении нередки случаи, когда применяются различные единицы измерения для одного и того же вида продукции. Это делается для того, чтобы полнее охарактеризовать потребительское назначение продукции и изменение ее состава. Например, производство электродвигателей учитывается в штуках и киловаттах мощности, бумаги - в тоннах и квадратных метрах, стальных труб - в тоннах и погонных метрах и т.п. При обобщении учетных данных широко используются стоимостные (денежные) единицы измерения. Для получения общего объема продукции в денежном выражении количество единиц каждого вида продукции в натуральном выражении умножается на цену соответствующего вида, а затем полученные произведения суммируют во всем видам. Абсолютные статистические показатели могут быть измерены с различной степенью точности. С переходом к более высоким ступеням обобщения применяются и более укрупненные единицы измерения. Например, производство металлорежущих станков на промышленном предприятии учитывается в штуках, а в масштабах страны - в миллионах штук; государственные закупки зерна в хозяйствах измеряются в тоннах, а по России в целом - в тысячах тонн. Соблюдение одноименных единиц измерения исследуемых показателей является важным исходным условием при международных сравнениях. Вместе с тем одноименные единицы измерения объема производства однотипной продукции в разных странах могут быть неодинаковыми по величине или методологии учета. Это касается, например, показателей производства электроэнергии, выпуска строительного кирпича и ряда других продуктов. Относительные величины Хотя абсолютные величины играют важную роль в практической и познавательной деятельности человека, анализ фактов обязательно приводит к необходимости различного рода сопоставлений. И тогда абсолютные показатели, характеризующие те или иные изучаемые явления, рассматриваются не только самостоятельно, но и в сравнении с другим показателем, который принимается за масштаб оценки или иначе за базу сравнения. Сопоставление статистических данных осуществляется в различных формах и по разным направлениям. В соответствии с различными задачами и направлениями сопоставления статистических данных применяются различные виды относительных величин. Сопоставлять можно одноименные показатели, относящиеся к различным периодам, различным объектам или разным территориям. Результат такого сопоставления может быть представлен коэффициентом (база сравнения принята за единицу) или выражен в процентах и показывает, во сколько раз или на сколько процентов сравниваемый показатель больше или меньше базисного. В результате соотношения одноименных показателей получают следующие относительные величины: относительные величины динамики; относительные величины выполнения плана и планового задания; относительные величины структуры; относительные величины координации; относительные величины наглядности. Относительная величина динамики характеризует изменение явления во времени и показывает, во сколько раз увеличился (или уменьшился) уровень показателя по сравнению с каким-либо предшествующим периодом. Для расчета относительной величины динамики определяют отношение уровней, характеризующих изучаемое явление в разные периоды времени. Численность населения Российской Федерации
В планах предприятий задания устанавливаются как в абсолютных показателях, так и в виде относительных величин, которые показывают, во сколько раз или на сколько процентов должна увеличиться (уменьшиться) величина показателя по плану в сравнении с его уровнем в предшествующем периоде. Например, по плану темп роста экспорта продукции предприятия должен был составить в 2008 г. (в % к предшествующему году) 106,1 %, относительная величина динамики объема экспорта продукции составила 107,3%. Сравнение двух относительных величин - планового задания и динамики - свидетельствует о перевыполнении плана по экспорту продукции предприятия в 2008 г. Степень выполнения плана оценивается с помощью относительной величины выполнения плана, которую получают отношением фактического уровня показателя в отчетном периоде к его уровню, запланированному на этот же период. Рассмотрим, как связаны между собой относительные величины планового задания, выполнения плана и динамики. Обозначим у0 - фактический уровень показателя в базисном периоде; упл - планируемый уровень показателя на отчетный период; у1 - фактический уровень показателя в отчетном периоде. Тогда в принятых обозначениях относительные величины могут быть представлены следующими соотношениями: Относительная величина планового задания Относительная величина выполнения плана Относительная величина динамики Следовательно, относительная величина динамики может быть получена произведением относительных величин планового задания и выполнения плана, т.е. Таким образом, в приводимом примере на основе относительных величин динамики и планового задания может быть определена относительная величина выполнения плана по росту экспорта продукции предприятия: или относительная величина выполнения плана составила 101,1%, а это означает, что план по росту экспорта продукции предприятия был перевыполнен в 2008 г. на 1,1 %. Относительные величины структуры характеризуют долю отдельных частей в общем объеме совокупности, их рассчитывают как отношение числа единиц (или объема признака) в отдельных частях совокупности к общей численности единиц (или объему признака) по всей совокупности. Относительные величины структуры рассчитываются по сгруппированным данным. Расчет относительных величин структуры за несколько периодов позволяет выявить структурные сдвиги. В целях анализа наряду с соотношением части и целого (показателями структуры) определяют соотношение между двумя частями одного целого. Относительные величины, характеризующие соотношение между частями одного целого, называют относительными величинами координации. К таким величинам относятся, например, показатели, характеризующие соотношение между численностью городского и сельского населения, между численностью рабочих и служащих, между численностью мужчин и женщин, между величиной заемного и собственного капитала банка и т.д. Относительные величины координации нередко характеризуются числом единиц одной части на 100 или 1000 единиц другой части. Например, в таблице показано, сколько безработных приходится на 1000 человек занятых в экономике России. Данные этой таблицы свидетельствуют об устойчивой тенденции увеличения соотношения численности безработных и занятых в экономике России за период с 2009 по 2012 гг. Соотношение численности безработных и занятых в экономике России
Относительные величины наглядности отражают результаты сопоставления одноименных показателей, относящихся к одному и тому же периоду (или моменту) времени, но к разным объектам или территориям. Этот вид относительных величин применяется для сравнительной оценки уровня развития стран и регионов, а также при оценке результатов деятельности отдельных предприятий отрасли. Обычно их исчисляют в процентах или кратных отношениях, показывающих во сколько раз одна из сравниваемых величин больше (или меньше) другой. Соотношение ожидаемой продолжительности жизни мужчин России и Дании в % к Норвегии в 2010 г.
Относительные величины наглядности находят широкое применение не только при международных сопоставлениях, но и при сравнительной оценке показателей деятельности предприятий и различных регионов. Так, могут сравниваться результаты работы предприятий различных форм собственности. Безусловный интерес представляет сопоставление цен на продукцию государственных и частных предприятий, средней заработной платы работников этих предприятий и т.д., принимая при этом цену и другие показатели государственных предприятий за базу сравнения. Отношения между разноименными абсолютными величинами называют относительными величинами интенсивности. Пример: потребление продуктов питания и непродовольственных товаров на душу населения, показатели обеспеченности населения предметами культурно-бытового и хозяйственного назначения длительного пользования в расчете на 100 семей или на 1000 человек населения; обеспеченности населения жильем и т.д. Учитывая экономическую сущность относительных величин интенсивности, их можно было бы назвать показателями уровня экономического и социального развития. Относительные величины интенсивности являются именованными числами (число аварий на 10 тыс. человек населения, производство хлопчатобумажных тканей в квадратных метрах на душу населения и т.д.). Цели и направления исследования определяют выбор вида относительных величин. Вместе с тем для полной характеристики различных сторон изучаемых явлений необходима система относительных величин, рассчитанных по ряду существенных признаков. Например, состав рабочих промышленного предприятия изучается по профессиям, полу, возрасту, уровню образования, стажу работы, квалификации, уровню механизации их труда, т.е. относительные величины структуры должны быть рассчитаны по группам, сформированным на основе вышеуказанных признаков. С другой стороны, важно выявить основные тенденции в изменении состава рабочих. Это требует сопоставления данных за ряд лет с помощью относительных величин динамики. Определенный интерес представляет сопоставление численности основных и вспомогательных рабочих и других относительных величин, позволяющих всесторонне характеризовать состав и движение рабочих. Важно отметить, что в процессе экономико-статистического анализа абсолютные и относительные величины должны рассматриваться во взаимосвязи, т.е. пользоваться относительными величинами нужно представлять, какая абсолютная величина скрывается за каждым относительным показателем. Виды средних величин и их значение в социально-экономических исследованиях В процессе обработки и обобщения статистических данных возникает необходимость определения средних величин. Как правило, индивидуальные значения одного и того же признака у различных единиц совокупности неодинаковы. Средняя величина -обобщающая характеристика изучаемого признака в исследуемой совокупности. Она отражает его типичный уровень в расчете на единицу совокупности в конкретных условиях места и времени. Пример: ЗП :30,25,15 средняя равна 23,3 т.р. Естественно, индивидуальные значения дохода отдельных рабочих отличаются от среднего уровня в силу ряда причин (квалификации, стажа работы, наличия акций, суммы вклада в имущество концерна и др.). Средний доход в свою очередь характеризует то общее, что свойственно всей совокупности рабочих предприятия, т.е. уровень дохода массы рабочих в конкретных условиях функционирования данного концерна в рассматриваемом периоде. Средние величины применяются для оценки достигнутого уровня изучаемого показателя, при анализе и планировании производственно-хозяйственной деятельности предприятий (объединений), фирм, банков и других хозяйственных единиц; средние используются при выявлении взаимосвязей явлений, при прогнозировании, а также расчете нормативов. Средняя величина всегда именованная, имеет ту же размерность (единицу измерения), что и признак у отдельных единиц совокупности. Основным условием научного использования средней величины является качественная однородность совокупности, по которой исчислена средняя. Прежде чем вычислять средние величины, необходимо произвести группировку единиц исследуемой совокупности, выделив качественно однородные группы. Средняя, рассчитанная по совокупности в целом, называется общей средней, средние, исчисленные для каждой группы, - групповыми средними. Общая средняя отражает общие черты изучаемого явления, групповая средняя дает характеристику размера явления, складывающуюся в конкретных условиях данной группы. Пример:
Групповые средние используются для изучения закономерностей развития общественных явлений. Так, в аналитических группировках анализ групповых средних позволяет сделать вывод о наличии и направлении взаимосвязи между группировочным (факторным) признаком и результативным показателем. Существуют две категории средних величин: степенные средние (к ним относятся средняя арифметическая, средняя гармоническая, средняя геометрическая и др.), а также структурные средние (мода и медиана). Выбор того или иного вида средней производится в зависимости от цели исследования, экономической сущности усредняемого показателя и характера имеющихся исходных данных. Рассмотрим пример. Известны значения стоимости ежедневников в 10 магазинах города в 2012 году.
Требуется определить среднюю стоимость ежедневника Общая сумма стоимости всех ежедневников 8550 тыс. руб., это определяющий показатель исчисленный как сумма индивидуальных значений стоимости ежедневника в каждом магазине Определяющий показатель, выраженный математически, называется определяющей функцией Зная определяющую функцию и уравнение средних где Х - индивидуальное значение признака каждой единицы совокупности; n - число единиц совокупности. Таким образом, средняя стоимость ежедневника вычисляется по формуле: Если бы все единицы изучаемой совокупности развивались под действием одних общих условий и на них не действовали никакие «случайные» факторы, то величина признака у каждой единицы - индивидуальное значение месячной заработной платы - была бы одинаковой, равной 855 руб. и обеспечивала величину итогового показателя: 855 руб. х 10 чел.=8550 руб. Способность средних величин сохранять свойства статистических совокупностей называют определяющим свойством. Общая формула степенной средней записывается следующим образом: 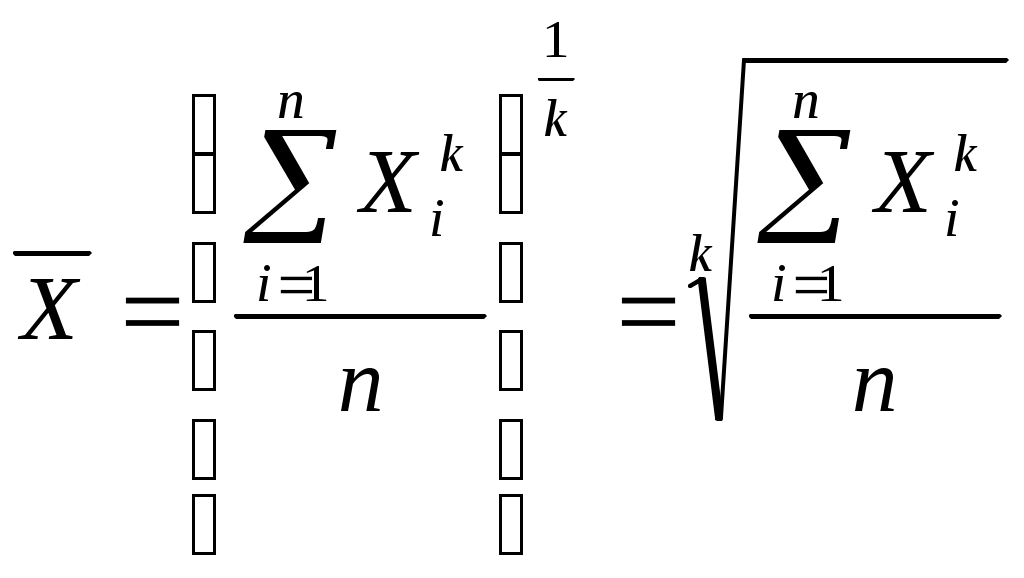 С изменением показателя степени K выражение данной функции меняется, и в каждом отдельном случае приходим к определенному виду средней. Запишем формулы различных видов степенных средних, придавая к значения: -1,0,1,2. Это простые средние (индивидуальные значения усредняемого признака не повторяются При к= -1 получим среднюю гармоническую величину: 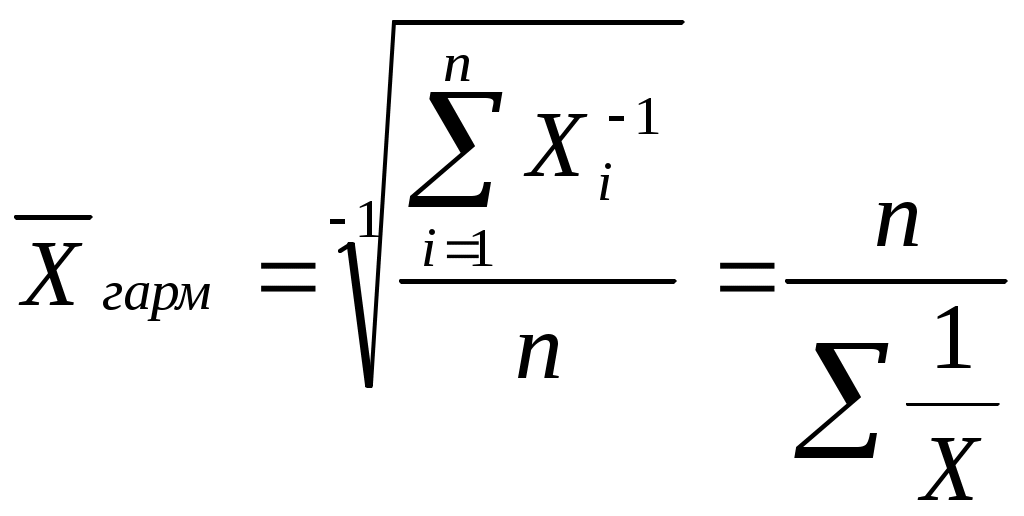 при к=0 получим среднюю геометрическую величину: 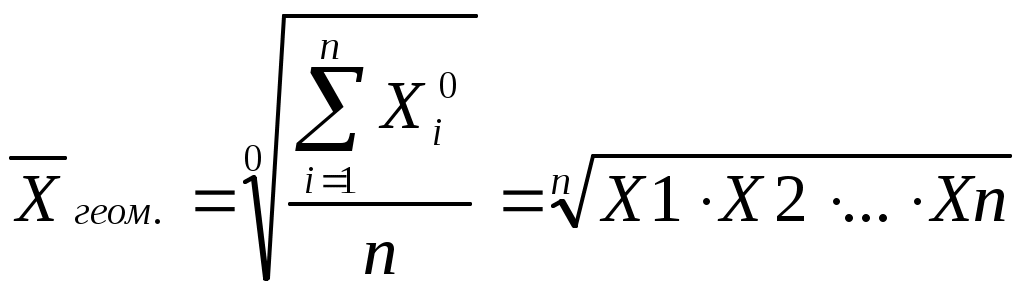 при к=1 получим среднюю арифметическую: 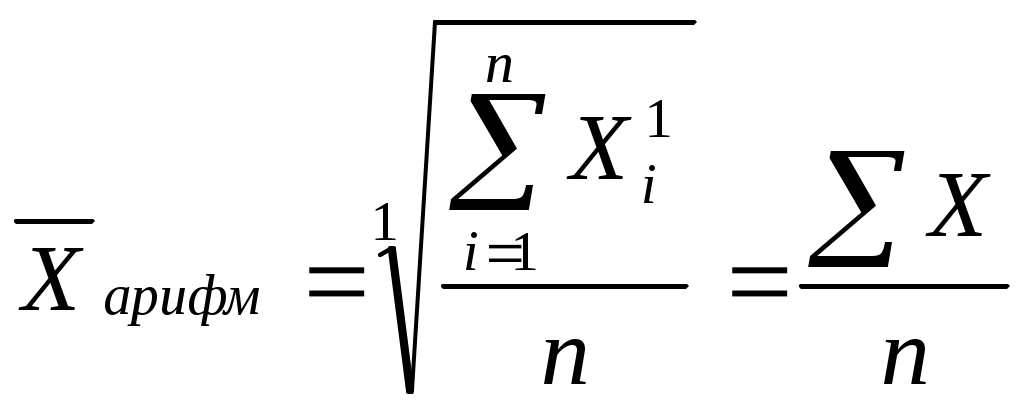 при к=2 получим среднюю квадратическую: 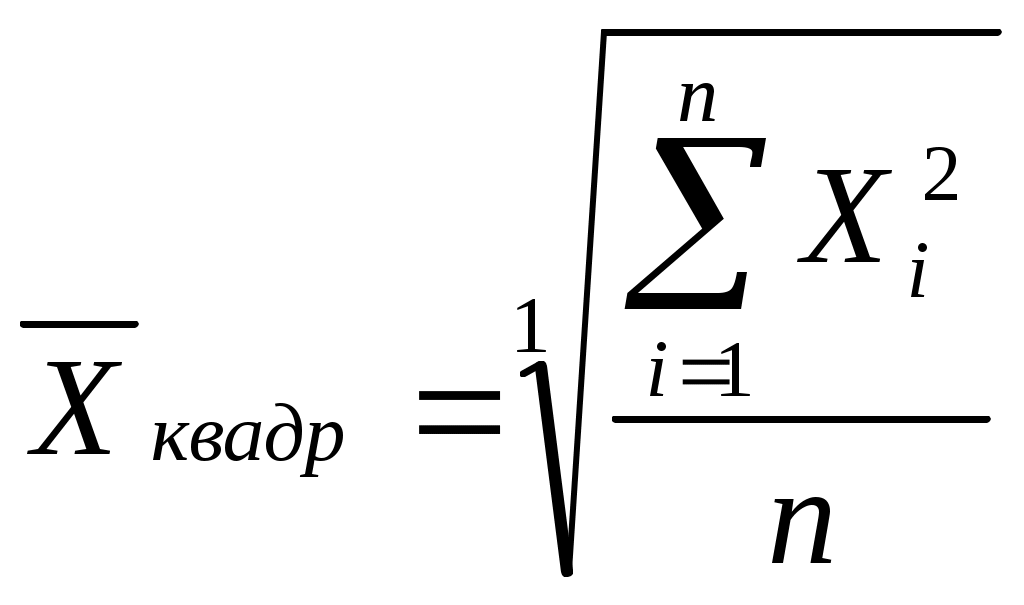 Когда в практических исследованиях отдельные значения изучаемого признака встречаются несколько раз у единиц исследуемой совокупности, тогда частота повторения индивидуальных значений признака (вес) присутствует в расчетных формулах степенных средних. В этом случае они называются формулами взвешенных средних и имеют следующий вид: средняя гармоническая 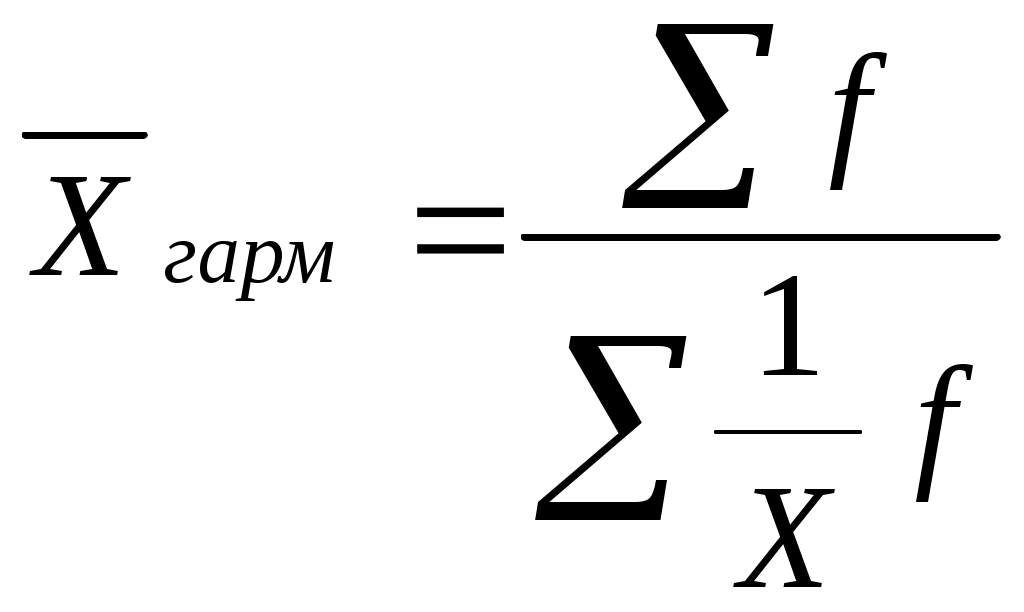 средняя геометрическая средняя арифметическая: средняя квадратическая: 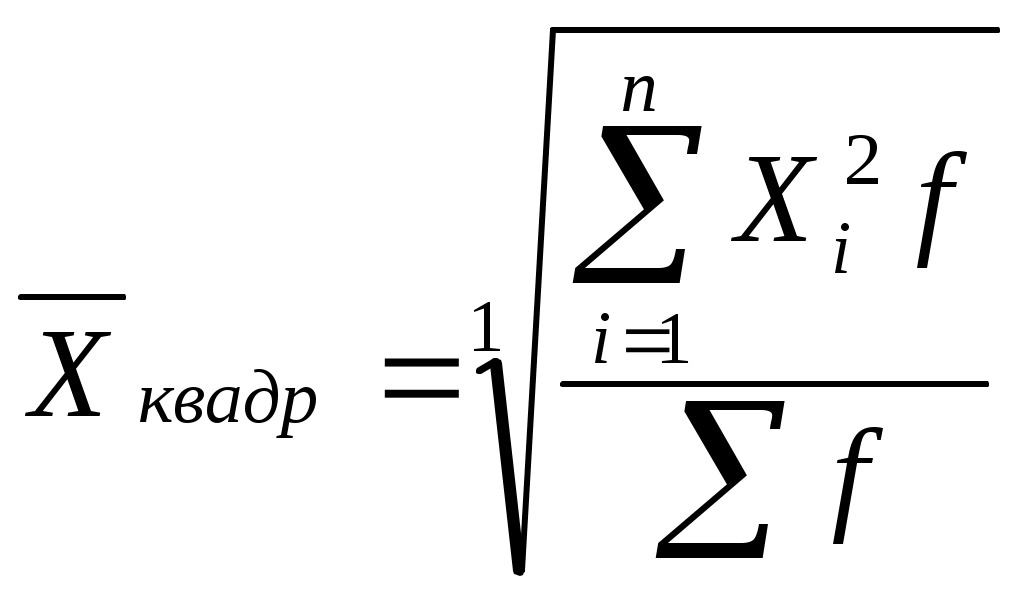 f- частота повторений индивидуального значения признака (его вес). Весом может быть и частость, т.е. отношение частоты повторения индивидуального значения признака к сумме частот: Известно, что степенные средние разных видов, исчисленные по одной и той же совокупности, имеют различные количественные значения. И чем больше показатель степени к, тем больше и величина соответствующей средней: 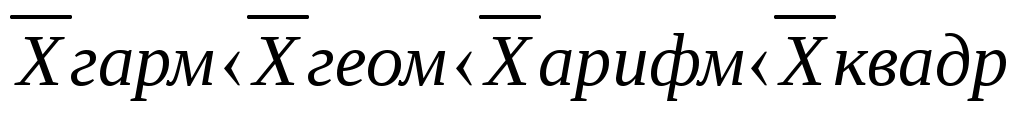 Это свойство степенных средних возрастать с повышением показателя степени определяющей функции называется мажорантностью средних. К средним величинам, кроме степенных средних, относят также моду и медиану. Мода и медиана определяются лишь структурой распределения Их называют структурными средними). Медиану и моду часто используют как среднюю характеристику в тех совокупностях, где расчет средней степенной невозможен или нецелесообразен. Например, обследование 12 магазинов позволило зафиксировать различные цены на изделия
В силу того, что исследователь не располагает данными об объеме продаж в каждом магазине, расчет средней арифметической с целью определения средней цены за изделие нецелесообразен. Однако можно определить то значение признака, которое делит единицы ранжированного ряда на две части. Такое значение носит название медианы. Медиана лежит в середине ранжированного ряда и делит его пополам. Расчет медианы по несгруппированным данным производится следующим образом: а) расположим индивидуальные значения признака в возрастающем порядке:
б) определим порядковый номер медианы по формуле: В нашем случае Это означает, что медиана в данном случае расположена между шестым и седьмым значениями признака в ранжированном ряду, так как ряд имеет четное число индивидуальных значений. Таким образом, Ме равна средней арифметической из соседних значений: 4550,4560. в) рассмотрим порядок вычисления медианы в случае нечетного числа индивидуальных значений. Допустим, мы наблюдали не 12, а 11 пунктов обмена валюты, тогда ранжированный ряд будет выглядеть следующим образом (отбрасываем 12-й пункт):
Находим номер медианы: на шестом месте стоит Х6=4560, который и является медианой: Ме - 4560 руб. Мода - это наиболее часто встречающееся значение признака у единиц данной совокупности. Она соответствует определенному значению признака. В нашем случае модальной ценой за доллар можно назвать 4560 руб.: это значение повторяется 4 раза, чаще, чем все другие. На практике моду находят, как правило, по сгруппированным данным. Определить величину моды в первичном ряду в точном соответствии с данным правилом возможно только при достаточно большом количестве наблюдений и при условии, что одно из индивидуальных значений изучаемого признака у отдельных единиц совокупности повторяется значительно чаще, чем все другие значения. В статистической практике из всех перечисленных выше видов средних чаше всего используется средняя арифметическая. Ее расчет осуществляется по-разному для несгруппированных и сгруппированных данных. Рассмотрим пример. Требуется вычислить средний стаж работы 12 работников рекламного агентства. При этом известны индивидуальные значения признака (стажа) в годах: 6, 4, 5, 3, 3, 5, 5, 6, 3, 7, 4, 5. Под средней арифметической понимается такое значение признака, которое имела бы каждая единица совокупности, если бы общий итог всех значений признака был распределен равномерно между всеми единицами совокупности. Заметим, что в нашем примере одно и то же значение признака встречается несколько раз. Объединив данные по величине признака и подсчитав число случаев повторения каждого из них, проведем расчет среднего стажа по сгруппированным данным с помощью формулы средней взвешенной арифметической.
Легко заметить, что средняя арифметическая взвешенная, по которой производился расчет в рассмотренном примере, не имеет принципиальных отличий от простой средней арифметической (средние, рассчитанные по разным формулам совпадают), просто суммирование f раз одного и того же значения признака (варианта) заменено в ней умножением варианта на f Однако естественно, что при этом величина средней зависит уже не только от величины индивидуальных значений признака (как в простой средней арифметической), но и от соотношения их весов (частот). Чем большие веса имеют малые значения вариантов, тем меньше величина средней и наоборот. При расчете средних по сгруппированным данным следует учитывать, что важное значение имеет обоснование и выбор веса при расчете средней арифметической взвешенной. Проиллюстрируем сказанное на следующем условном примере. Имеются данные о доле экспорта в стоимости товарной продукции предприятий, выпускающих минеральные удобрения.
Средняя доля экспорта, исчисленная как средняя арифметическая взвешенная по числу предприятий, является формальной средней. Логически обоснованным можно считать выбор в качестве весов объемов товарной продукции в каждой группе предприятий с определенной долей экспорта, поскольку доля экспорта получается делением объема экспорта на товарную продукцию предприятия. Теперь в числителе мы получили общую стоимость экспортной продукции, а в знаменателе—общую стоимость всей товарной продукции (16 предприятий). Таким образом, в результате расчета определена средняя доля экспорта предприятий исследуемой совокупности, равная 0,24 (24%) |
