Абсолютно твердое тело. Абсолютно твердое тело м еханическим движением
 Скачать 28.74 Kb. Скачать 28.74 Kb.
|
|
Абсолютно твердое тело Механическим движением называется изменение взаимного положения тел или частей одного тела в пространстве с течением времени. Механика для описания движения тел в зависимости от условий конкретных задач использует разные физические модели. Простейшей моделью является материальная точка — тело, обладающее массой, размерами которого в данных условиях можно пренебречь. Понятие материальной точки — абстрактное, но его введение облегчает решение практических задач. Например, изучая движение планет по орбитам вокруг Солнца, можно принять их за материальные точки. Произвольное макроскопическое тело или систему тел можно мысленно разбить на малые взаимодействующие между собой части, каждая из которых рассматривается как материальная точка. Тогда изучение движения произвольной системы тел сводится к изучению системы материальных точек. В механике сначала изучают движение одной материальной точки, а затем переходят к изучению движения системы материальных точек. Под воздействием тел друг на друга тела могут деформироваться, т. е. изменять свою форму и размеры. Поэтому в механике вводится еще одна модель — абсолютно твердое тело. Абсолютно твердым телом называется тело, которое ни при каких условиях не может деформироваться и при всех условиях расстояние между двумя точками (или точнее между двумя частицами) этого тела остается постоянным. Любое движение твердого тела можно представить как комбинацию поступательного и вращательного движений. Поступательное движение — это движение, при котором любая прямая, жестко связанная с движущимся телом, остается параллельной своему первоначальному положению. Вращательное движение — это движение, при котором все точки тела движутся по окружностям, центры которых лежат на одной и той же прямой, называемой осью вращения. Движение тел происходит в пространстве и во времени. Поэтому для описания движения материальной точки надо знать, в каких местах пространства эта точка находилась и в какие моменты времени она проходила то или иное положение. Положение материальной точки или тела в пространстве можно определить только относительно какого-нибудь другого тела. Тело, относительно которого рассматривается механическое движение данного тела, называется телом отсчета. Пространственное положение движущегося тела в произвольный момент времени обычно задается в системе координат, начало которой жестко связано с телом отсчета. В декартовой системе координат, используемой наиболее часто, положение точки А в данный момент времени по отношению к этой системе характеризуется тремя координатами х, у и z или радиусом-вектором r, проведенным из начала системы координат в данную точку (рис.). 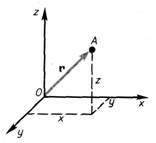 Координаты с течением времени изменяются, т.е. представляют собой функции времени. В общем случае движение материальной точки определяется скалярными уравнениями x = x(t), y = y(t), z = z(t), что эквивалентно векторному уравнению Эти уравнения называются кинематическими уравнениями движения материальной точки. Положение тела (точки) на линии, плоскости или в пространстве определяют, соответственно, одной, двумя или тремя координатами. Тело отсчета, жестко связанная с ним система координат и прибор для измерения времени (часы) называется системой отсчета. Движущаяся точка описывает в заданной системе отсчета линию, которую называют траекторией. По форме траектории движения разделяются на прямолинейные и криволинейные. Прямолинейным называется движение, траектория которого является прямая линия. Криволинейным называется движение, траектория которого - кривая линия. Примером криволинейного движения может быть движение тела по окружности, движение тела, брошенного горизонтально и под углом к горизонту. Форма траектории зависит от выбора системы отсчета. Пройденное точкой расстояние от начального пункта движения до конечного вдоль траектории называется длиной пути (или просто путь), который точка прошла за некоторый промежуток времени. Итак, расстояние, измеряемое вдоль траектории, называется путем. Путь является скалярной величиной, ибо не указывает направления движения. Путь определяется по формуле S = vt, где v - скорость, также скалярная величина, показывающая численное значение длины пути, пройденного телом за единицу времени; t - время. Он измеряется в метрах (или других единицах длины) и показывает, как далеко переместилась точка по своей траектории, но ничего не говорит о том, в какую сторону она переместилась и где, следовательно, находится в данный момент. Для определения положения в произвольный момент времени надо знать не пройденный путь, а его перемещение. Перемещение — вектор, соединяющий начальное и конечное положения тела (материальной точки). Путь и перемещение — разные физические величины. Поясним это на рисунке. 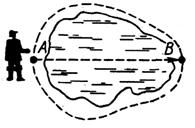 Предположим, человек должен перебраться с одного берега на другой. Он может обойти озеро в одном или другом направлении или же переплыть на лодке. В любом случае конечная точка одна и та же, но пути человека будут неодинаковой длины. Вектор перемещения не совпадает с траекторией точки. Они совпадают только при прямолинейном движении. Таким образом, перемещение - величина векторная и определяется формулой где v - вектор скорости. Пусть точка А начального положения тела, движущегося прямолинейно и равномерно, определена координатой х0, тогда через время t оно окажется в точке В с координатой х. Перемещение АВ = Таким образом, зная координаты начального положения тела и вектор скорости, можно точно указать координаты нахождения тела в любой момент времени. При прямолинейном движении вектор перемещения совпадает с соответствующим участком траектории и модуль перемещения |
