физхимия экзамен ответ. 9 билет. Адиабатические процессы происходящие без теплообмена с окружающей средой
 Скачать 1.6 Mb. Скачать 1.6 Mb.
|
|
Билет 9 • Простые реакции – совокупность однотипных элементарных химических актов, представляющих собой превращение реагентов в продукты за короткий отрезок времени (порядка 10--13 с для адиабатических и 10--15 с для неадиабатических реакций). Адиабатические – процессы происходящие без теплообмена с окружающей средой. Неадиабатические – происходит обмен теплотой. • Сложные реакции – включают несколько элементарных (простых) стадий. В основе кинетики сложных реакций лежит принцип независимости отдельных стадий. Согласно этому принципу, если в системе протекает несколько реакций, каждая из них идет независимо от другой и подчиняется закону действующих масс. Полное изменение в системе является суммой изменений, внесенных всеми этими независимыми реакциями. Математически это означает, что кинетическое уравнение сложной реакции представляет собой алгебраическую сумму кинетических уравнений составляющих ее простых реакций. Этот принцип справедлив не всегда, в частности он неприменим для сопряженных реакций. Обратимые реакции первого рода. В общем виде обратимую мономолекулярную реакцию можно записать следующим образом: к1 А=Б к2 Если a и b – начальные концентрации веществ A и B, а x – концентрация прореагировавшего за время t вещества, то dx\dt=k1(a-x)-k2(b+x) Это выражение получается, если учесть, что скорость обратимой реакции равна разности скоростей прямой и обратной реакций. Преобразуем последнее выражение, раскрывая скобки и вынося за скобки k1 + k2:  Параллельные реакции первого порядка  (тут про принцип независимости) (тут про принцип независимости)  Задача 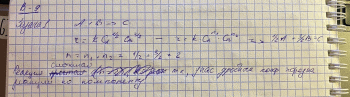 2 Основой теории активных столкновений (соударений) [ТАС] является кинетической теории газов: - Газ состоит из множества частиц (молекул) с массой m, находящихся в непрерывном беспорядочном движении. Частицы (молекулы) имеют малые размеры (диаметры) по сравнению со средним расстоянием между ними. - Молекулы являются бесструктурными частицами. - Траектории между двумя столкновениями представляют прямые линии. • Кинетическая теория газов – соударения между частицами абсолютно упругие, т. е. общая поступательная кинетическая энергия сталкивающейся пары одинакова до и после столкновения: энергия ни одной из сталкивающихся частиц (молекул) не переходит во вращательную, колебательную или другие виды энергии. Основные положения ТАС: Теория ТАС применима к бимолекулярным реакциям второго порядка. - Частицы (молекулы) имеют сферическую форму. - Акт превращения реагентов в продукты совершается в момент столкновения активных молекул и протекает мгновенно. В действительности химические реакции происходят путем постепенной перестройки молекул и перераспределения энергии между химическими связями. В ТАС получены два основных выражения для константы скорости бимолекулярной реакции. Для реакции между разными молекулами (A + B 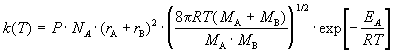 (9.1) (9.1)Здесь NA - постоянная Авогадро, r - радиусы молекул, M - молярные массы веществ. Множитель в больших круглых скобках - это средняя скорость относительного движения частиц A и B. Константа скорости бимолекулярной реакции между одинаковыми молекулами (2A 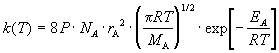 (9.2) (9.2)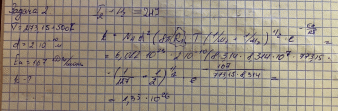 Гомогенный катализ. Допустим, реакция в отсутствие катализатора между веществами А и В протекает с образованием активированного комплекса AB : A + B = AB = C + D. В присутствии катализатора K процесс идет в несколько стадий: 1, 2) A + K (k1/k2)AK (обратимое образование промежуточного продукта), 3) AK + B (k3) ABK (образование активированного комплекса), 4) ABK (k4) C + D + K (разложение активированного комплекса). Кинетика гомогенно-каталитической реакции зависит от свойств промежуточного продукта AK. Наблюдаемая скорость реакции равна скорости мономолекулярного распада активированного комплекса: 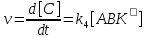 Основные виды гомогенного катализа Кислотно – основной (Катализатор – кислота или основание) - HF, Н2SО4 Ферментативный катализ Метало –комплексный ( катализатор – ионы металлов , металокомплексные соединения) Кислотно – основной катализ. По Аррениусу (1884 г) кислота – это соединение, образующее при диссоциации в воде ионы водорода H3O+, а основание – это соединение, образующее при диссоциации в воде гидроксид - ионы OН- По Дж.Брестеду и Т.Лоури (1923 г) кислота – это вещество, являющее донором протона, а основание – вещество, являющее акцептором протона. В растворе существует кислотно – основное равновесие: По Г.Льюису кислота – это акцептор неподеленной пары электронов, а основание – вещество, являющее донором электронной пары. 4 Закон Шредингера Закон Шредингера представляет собой характеристику движения частицы в квантовой механике. Самое простое уравнение выглядит следующим образом: 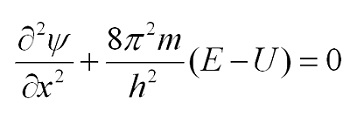 где x - координата частицы, а E и U – ее полная и потенциальная энергии соответственно. где x - координата частицы, а E и U – ее полная и потенциальная энергии соответственно. Решить уравнение Шредингера значит найти собственную функцию оператора Ĥ и собственную энергию оператора. Решение для атома водорода. 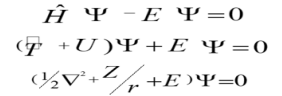 Решение уравнения Шредингера сводится к следующему алгоритму: 1) Переходим от декартовой системы координат к сферической и записываем оператор (х,у,z) = (r,,), который имеет сложный вид 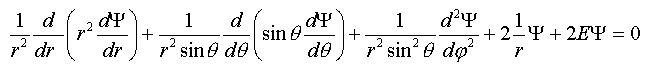 2) Задаем волновую функцию (r,,) в виде произведения трех функций, каждая из которых зависит от одной переменной: 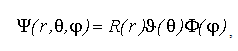 3) Математическими преобразованиями преобразуем уравнение так, чтобы получить три уравнения, каждое из которых зависит только от одной функции : R(r) или () или Ф(). При этом если мы получаем равенство двух уравнений, зависящих от разных переменных, то оба эти равнения равны некоторой постоянной величине, т. о. получаются математические константы – l и m.  Окончательно (r, , )= Rn,l(r)* l,m ()* m () = f(n,l,m), где n – главное квантовое число; l – побочное или азимутальное квантовое число m – магнитное квантовое число. Полученное выражения для (r, , ) характеризует основное понятие квантовой химии- атомной орбитали (АО). Решение уравнения Шредингера для многоэлектронного атома Самая простая многоэлектронная модель это атом гелия Не, который содержит 2 е. Уравнение Шредингера имеет вид: Ĥ(r, , ) = E*(r, , ). Для упрощение уберем обозначение координат; Ĥ= E* или Ĥ- E* = 0. Выражение для оператора полной энергии ( Гамильтониан) Ĥ имеет вид: Ĥ = Ť + Û , где Ĥ - оператор полной энергии или Гамильтониан системы Ť - оператор кинетической энергии системы Û – оператор потенциальной энергии системы. После подстановки получим: (Ť + Û )- E* = (Ť + Û - Е) = 0. Оператор кинетической энергии для любой частицы имеет вид: Ťi = -(ħ2/2mi)*i2 Оператор кинетической энергии системы определяется через сумму операторов кинетической энергии для каждой частицы, составляющих систему. При переходе к атомным единицам: Ť = Ti = -1/2∇2е1 - 1/2∇2е2 а.е. Оператор потенциальной энергии системы совпадает с классическим значением потенциальной энергии и определяется через сумму потенциальной энергии парного взаимодействия Uij для каждой пары частицы, составляющих систему. При переходе к атомным единицам Û = U = Uij = Ue1я + Ue2я + Ue1e2 = - Z/r1- Z/r2- + 1/r12 а.е. После подстановки в уравнение Шредингера выражения для операторов Т и U получим окончательный вид уравнения Шредингера: (1/2∇2е1+1/2∇2е2 + E + Z/r1+ Z/r2 - 1/r12) =0 - для двух электронов Или в более общем виде: 1/2∇2i + E + Z/ri - 1/rij) =0 Как видно в уравнение входит rij, которое не постоянно (электроны непрерывно двигаются), что не позволяет точно решить уравнение. Вывод: наличие в уравнении Шредингера выражения для потенциальной энергии отталкивания электронов Ueiej = 1/rij не позволяет точно решить уравнение Шредингера для многоэлектронных атомов, т.к. расстояние между электронами не постоянно. • ЭЛЕКТРОННОЙ КОНФИГУРАЦИЕЙ – называется распределение электронов атома по различным квантовым состояниям (или спин-орбиталям). Общий вид: Пnili^k, где k - количество электронов на данной АО или подуровне (т.е. общее кол-во на всех АО с одинаковым значением l). Например для атома H - 1s1 , He - 1s2 , C - 1s2 2s2 2p2 . Несмотря на широкое применение электронной конфигурации такая форма записи имеет существенный недостаток, т.к. не дает информацию о реальном распределении электронов по квантовым ячейкам. • АТОМНЫЙ ТЕРМ – энергетическая характеристика распределения электронов в атоме. Общее выражение для атомного терма, описывающего общее состояние многоэлектронного атома для схемы Рассел -Саундерса (Энергетическая характеристика):  Величина M = 2S + 1 называется мультиплетностью и показывает число линий на которое расщепляется основной сигнал. Терм основного состояния (с мин. энергии) можно определить по максимальным значениям результирующих квантовых чисел. L =[ mi ] , S = [ msi ]  Результирующий спиновой – орбитальный момент для легких элементов Рассел-Саундерса J (L-S связь). Результирующий спиновой – орбитальный момент определяется по формулам, соответствущие рядам Клебша -Гордона: J = L+S, L+S -1, ……, L-S с шагом J = 1 Для определения энергии микросостояния, нас будет интересовать только два значения: минимальное Jmin = L-S и максимальное Jmax = L+ S Общее число вырожденных состояний ( число микросостояний с одинаковой энергией) для терма равно gJ = (2L + 1)(2S + 1) Магнитные свойства атомов. Если электроны спарены, то диамагнетик. Если электроны не спарены, то парамагнетик. |
