Алгоритмы поиска простых чисел. Алгоритмы поиска простых чисел

• Название: Алгоритмы поиска простых чисел
• Дата: 08.08.2022
• Размер: 246.15 Kb.
• Имя файла: Алгоритмы поиска простых чисел.docx
• Тип: Курсовая; #642646

ПРИДНЕСТРОВСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ

ИМ. Т. Г. ШЕВЧЕНКО

Физико-математический факультет

Кафедра прикладной математики и информатики

КУРСОВАЯ РАБОТА

по дисциплине «ПРОГРАММИРОВАНИЕ»

на тему:

«АЛГОРИТМЫ ПОИСКА ПРОСТЫХ ЧИСЕЛ»

Выполнила:

студентка VI курса, 62 гр., з/о

Токаренко И. В.

Проверил:

ст. преподаватель

Калинкова Е. В.

Тирасполь, 2022

Оглавление

ВВЕДЕНИЕ 4

1.Цели и задачи 4

2.Теоретические сведения 6

2.1Алгоритмы проверки на простоту 6

2.1.1Простой алгоритм перебором 6

2.1.2Алгоритм пробное деление 6

2.1.3 Тест Миллера – Рабина 7

2.2Числа – близнецы 7

2.3 Разложение на простые множители 7

3.Программная реализация 9

3.1Проверка на простоту 9

3.1.1Простой алгоритм перебором 9

3.1.2Простой алгоритм пробное деление 10

3.1.3Тест Миллера-Рабина 13

3.2Нахождение простых чисел в заданном интервале 15

3.2.1Простой алгоритм перебором 15

3.2.2Простой алгоритм пробное деление 17

3.2.3Тест Миллера-Рабина 18

3.3Поиск пар чисел близнецов 21

3.4Разложение на простые множители 24

ЗАКЛЮЧЕНИЕ 28

Список литературы 29

ВВЕДЕНИЕ

Простые числа – это такие числа, которые имеют только два делителя. Один из них – единица, а другое – само число. Иначе числа называются составными.

Некоторые ошибочно полагают, что наименьшее простое число – это единица.

С одной стороны, в этом есть логика, так как 1 делится только на 1. Но это получается одно и то же число (единица), что противоречит определению простых чисел, в котором четко прописано – «делителей должно быть два».

Количество простых чисел не ограничено. Или говоря математическим языком, оно стремится к бесконечности.

Поиск простых чисел — по крайней мере больших простых чисел — довольно сложная задача, потому что еще никому не удалось найти формулу или алгоритм, позволяющий генерировать любые простые числа. Но может возникнуть логичный вопрос: «Для чего нужно генерировать простые числа?»

На этот вопрос можно дать два ответа. Первый из них имеет теоретическое значение. Попытки генерации простых чисел ведут к появлению новых интересных инструментов для расчетов, особенно для компьютерных вычислений. Кроме того, наличие большого списка простых чисел позволяет проверять теоремы, которые еще не доказаны. Если кто-то выдвигает гипотезу относительно простых чисел, но оказывается, что одно из миллионов чисел нарушает ее, то вопрос снимается. Это стимулирует поиск простых чисел различных видов: простых чисел Мерсенна, чисел-близнецов и так далее.

Есть и другая причина, связанная с так называемым шифрованием. Электронная почта, банковские операции, кредитные карты и мобильная телефонная связь — все это защищено секретными кодами, непосредственно основанными на свойствах простых чисел.

1. Цели и задачи

Цель курсовой работы:

• 
  изучить различные алгоритмы поиска простых чисел;
  
• 
  разработать приложение с графическим интерфейсом на языке программирования С#, реализующее эти алгоритмы.
  

Программы должна решать ряд задач, связанных с поиском простых чисел:

Задача 1. Определение простого числа.

Задача 2. Нахождение простых чисел в заданном интервале.

Задача 3. Поиск пар чисел близнецов.

Задача 4. Разложение числа на простые множители.

При решении задачи 1 и задачи 2 рассмотреть различные алгоритмы. При решении задачи 2 и 4 предусмотреть возможность сохранения результатов в файл.

2. Теоретические сведения

   1. Алгоритмы проверки на простоту

      1. Простой алгоритм перебором

Небольшое число легко проверить на простоту – достаточно в цикле перебрать все числа от 2 до N – 1 и проверить не делится ли N на них без остатка.

2. Алгоритм пробное деление

Учитывая введенное число n , проверяется, делится ли оно без остатка на любое простое число от 2 до 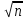(т.е. что при делении не остается остатка). Если да, то n является композитом . В противном случае он прост.

На самом деле, когда проверяются все возможные делители до, обнаруживаются некоторые множители дважды. Все уникальные делители n являются числами, меньшими или равными 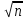, поэтому не нужно искать за этим. Все четные числа больше 2 также могут быть исключены, поскольку, если четное число может делить n , то может и 2.

Можно улучшить этот метод и дальше. Все простые числа больше 3 имеют форму 6 k ± 1 , где k - любое целое число больше 0. Это потому, что все целые числа могут быть выражены как (6 k + i) , где i = −1, 0, 1 , 2, 3 или 4. Нужно обратить внимание, что 2 делит (6 k + 0), (6 k + 2) и (6 k + 4), а 3 делит (6 k + 3) . Итак, более эффективный метод - проверить, делится ли n на 2 или 3, а затем проверить все числа в форме.

Обобщая далее, все простые числа больше, чем c # (примитив c), имеют форму c # · k + i , для i < c #, где c и k - целые числа, а i представляет числа, взаимно простые с c #.

При c → ∞ количество значений, которые c # k + i может принимать в определенном диапазоне, уменьшается, и поэтому время проверки n уменьшается. Для этого метода также необходимо проверить делимость на все простые числа, меньшие c.

2.1.3 Тест Миллера – Рабина

Тест на простоту Миллера – более сложный вариант, который обнаруживае все составные части (опять же, это означает: для каждого составного числа n не менее 3/4 чисел a являются свидетелями составности n). Это тоже тест на композитность.

Тест простоты Миллера – Рабина работает следующим образом: для заданного целого числа n выберается некоторое положительное целое число a  <  n . Пусть 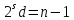, где d нечетное. Если

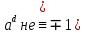mod n),

а также



тогда n составное, а a - свидетель составного. В противном случае n может быть простым, а может и не быть.

2. Числа – близнецы

Числа-близнецы (парные простые числа) — пары простых чисел, отличающихся на 2.

Все пары чисел-близнецов, кроме (3, 5), имеют вид {\displaystyle 6n\pm 1,}6n±1, так как числа с другими вычетами по модулю 6 делятся на 2 или на 3. Если учитывать также делимость на 5, то окажется, что все пары близнецов, кроме первых двух, имеют вид {\displaystyle 30n\pm 1}{\displaystyle 30n+12\pm 1}30n ± 1, 30n + 12 ± 1 либо {\displaystyle 30n+18\pm 1}30n +18 ± 1. Для любого целого {\displaystyle m\geqslant 2}m ≥ 2 пара {\displaystyle (m,m+2)}(m, m+2) является парой чисел-близнецов тогда и только тогда, если {\displaystyle 4[(m-1)!+1]+m}4 [(m-1)! +1] делится на {\displaystyle m(m+2)}m (m + 2) (следствие теоремы Вильсона).

Предполагается, что таких пар бесконечно много, но это не доказано. По первой гипотезе Харди — Литтлвуда, количество  пар простых-близнецов, не превосходящих  асимптотически приближается к

{\displaystyle \pi _{2}(x)\sim 2C_{2}\int \limits _{2}^{x}{\frac {dt}{(\ln t)^{2}}},} ,

где {\displaystyle C_{2}}  — константа простых-близнецов.

{\displaystyle C_{2}=\prod _{p\geq 3}\left(1-{\frac {1}{(p-1)^{2}}}\right)\approx 0.6601618158468695739278121100145\ldots }

2.3 Разложение на простые множители

Простой множитель — это множитель, который представляет собой простое число.

Разложение на простые множители — это представление составного числа в виде произведения простых множителей.

Разложить составное число на простые множители — значит представить это число в виде произведения простых множителей.

Простые множители в разложении числа могут повторяться. Повторяющиеся простые множители можно записывать более компактно — в виде степени.

Последовательность действий при разложении числа на простые множители:

1. 
   Проверяем по таблице простых чисел, не является ли данное число простым.
   
2. 
   Если нет, то последовательно подбираем самое маленькое простое число из таблицы простых чисел, на которое данное число делится без остатка, и выполняем деление.
   
3. 
   Проверяем по таблице простых чисел, не является ли полученное частное простым числом.
   
4. 
   Если нет, то последовательно подбираем самое маленькое простое число из таблицы простых чисел, на которое полученное частное делится нацело, и выполняем деление.
   
5. 
   Повторяем пункты 3 и 4 до тех пор, пока в частном не получится единица.
   

3. Программная реализация

   1. Проверка на простоту

      1. Простой алгоритм перебором

Листинг:

public bool IsPrime(int number)

{

for (int i = 2; i < number; i++)

{

if (number % i == 0)

return false;

}

return true;

}

private void button1_Click(object sender, EventArgs e)

{

if (numericUpDown1.Value<3)

{

MessageBox.Show("Число должно быть больше 2.");

return;

stopwatch.Start();

if (IsPrime(Convert.ToInt32(numericUpDown1.Value)))

{

label2.Text = "Число является простым";

label2.Fore

Color = Color.Green;

} else

{

label2.Text = "Число не является простым";

label2.ForeColor = Color.Red;

}

stopwatch.Stop();

label8.Text = "Время выполнения: " + stopwatch.ElapsedMilliseconds + "мсек.";

}

Экранная форма метода представлена на Рисунках 1-2.



Рисунок 1. Экранная форма метода простого перебора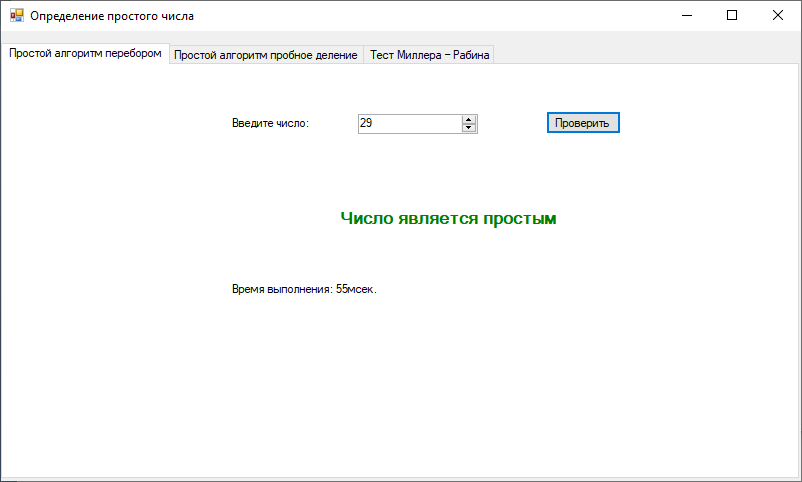



Рисунок 2. Экранная форма метода простого перебора

2. Простой алгоритм пробное деление

Листинг:

bool IsPrime2(int n)

{

if (n == 2 || n == 3)

return true;

if (n <= 1 || n % 2 == 0 || n % 3 == 0)

return false;

for (int i = 5; i * i <= n; i += 6)

{

if (n % i == 0 || n % (i + 2) == 0)

return false;

}

return true;

}

private void button2_Click(object sender, EventArgs e)

{

if (numericUpDown2.Value < 3)

{

MessageBox.Show("Число должно быть больше 2.");

return;

}

Stopwatch stopwatch = new Stopwatch();

stopwatch.Start();

if (IsPrime2(Convert.ToInt32(numericUpDown2.Value)))

{

label4.Text = "Число является простым";

label4.ForeColor = Color.Green;

}

else

{

label4.Text = "Число не является простым";

label4.ForeColor = Color.Red;

}

stopwatch.Stop();

label9.Text = "Время выполнения: " + stopwatch.ElapsedMilliseconds + "мсек.";

}

Экранная форма метода представлена на Рисунках 3-4.



Рисунок 3. Экранная форма метода пробного деления


Рисунок 4. Экранная форма метода пробного деления

3. Тест Миллера-Рабина

Листинг:

public bool MillerRabinTest(BigInteger n, int k)

{

// если n == 2 или n == 3 - эти числа простые, возвращаем true

if (n == 2 || n == 3)

return true;

// если n < 2 или n четное - возвращаем false

if (n < 2 || n % 2 == 0)

return false;

// представим n − 1 в виде (2^s)·t, где t нечётно, это можно сделать последовательным делением n - 1 на 2

BigInteger t = n - 1;

int s = 0;

while (t % 2 == 0)

{

t /= 2;

s += 1;

}

// повторить k раз

for (int i = 0; i < k; i++)

{

// выберем случайное целое число a в отрезке [2, n − 2]

RNGCryptoServiceProvider rng = new RNGCryptoServiceProvider();

byte[] _a = new byte[n.ToByteArray().LongLength];

BigInteger a;

do

{

rng.GetBytes(_a);

a = new BigInteger(_a);

}

while (a < 2 || a >= n - 2);

// x ← a^t mod n, вычислим с помощью возведения в степень по модулю

BigInteger x = BigInteger.ModPow(a, t, n);

// если x == 1 или x == n − 1, то перейти на следующую итерацию цикла

if (x == 1 || x == n - 1)

continue;

// повторить s − 1 раз

for (int r = 1; r < s; r++)

{

// x ← x^2 mod n

x = BigInteger.ModPow(x, 2, n);

// если x == 1, то вернуть "составное"

if (x == 1)

return false;

// если x == n − 1, то перейти на следующую итерацию внешнего цикла

if (x == n - 1)

break;

}

if (x != n - 1)

return false;

}

// вернуть "вероятно простое"

return true;

}

private void button3_Click(object sender, EventArgs e)

{

if (raund.Value<1)

{

MessageBox.Show("Kоличество раундов проверки должно быть больше 0.");

return;

}

stopwatch.Start();

if (MillerRabinTest((BigInteger)numer.Value, Convert.ToInt32(raund.Value)))

{

label5.Text = "Число является вероятно простым";

label5.ForeColor = Color.Green;

}

else

{

label5.Text = "Число является составным";

label5.ForeColor = Color.Red;

}

stopwatch.Stop();

label10.Text = "Время выполнения: " + stopwatch.ElapsedMilliseconds + "мсек.";

}

Экранная форма метода представлена на Рисунках 5-6.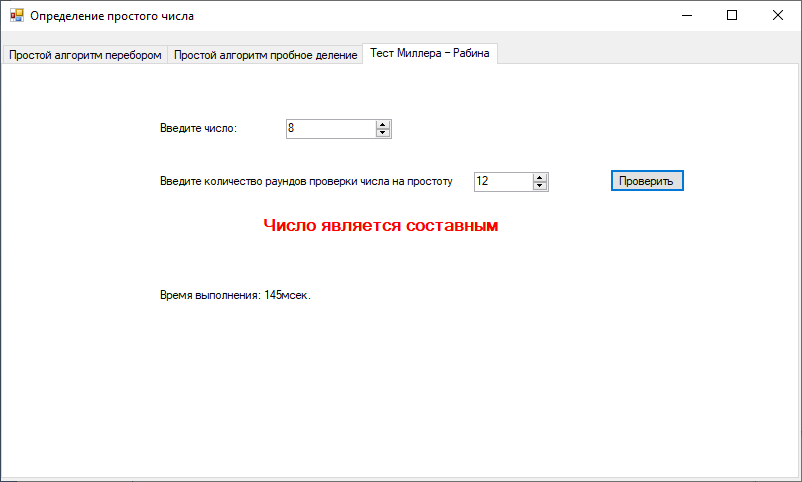



Рисунок 5. Экранная форма Тест Миллера-Рабина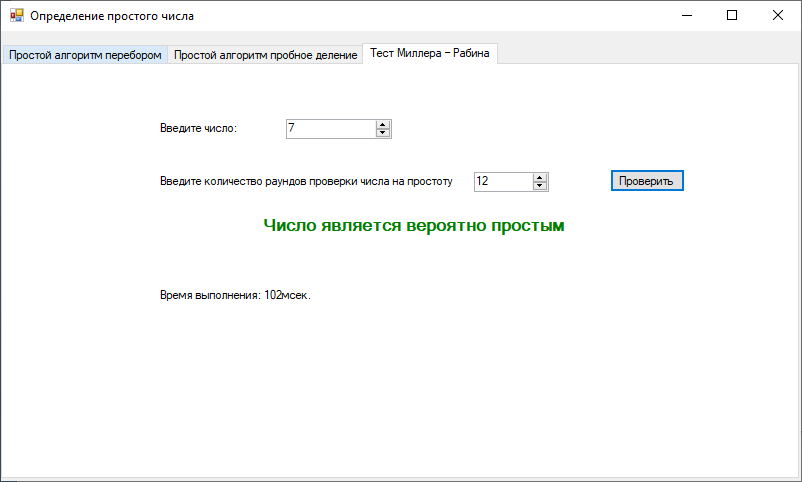


Рисунок 6. Экранная форма Тест Миллера-Рабина

2. Нахождение простых чисел в заданном интервале

   1. Простой алгоритм перебором

Листинг:

public bool IsPrime(int number)

{

for (int i = 2; i < number; i++)

{

if (number % i == 0)

return false;

}

return true;

}

private void button1_Click(object sender, EventArgs e)

{

if(start1.Value >= end1.Value)

{

listBox1.Items.Clear();

MessageBox.Show("Начало диапазона должно быть меньше конца диапазона !");

return;

}

stopwatch.Start();

for (decimal i=start1.Value;i<=end1.Value;i++)

{

if (IsPrime(Convert.ToInt32(i)))

{

listBox1.Items.Add(i);

}

}

stopwatch.Stop();

label8.Text = "Время выполнения: " + stopwatch.ElapsedMilliseconds + "мсек.";

}

Экранная форма метода представлена на Рисунке 7.



Рисунок 7. Экранная форма метода простого перебора

2. Простой алгоритм пробное деление

Листинг:

bool IsPrime2(int n)

{

if (n == 2 || n == 3)

return true;

if (n <= 1 || n % 2 == 0 || n % 3 == 0)

return false;

for (int i = 5; i * i <= n; i += 6)

{

if (n % i == 0 || n % (i + 2) == 0)

return false;

}

return true;

}

private void button2_Click(object sender, EventArgs e)

{

listBox2.Items.Clear();

if (start2.Value >= end2.Value)

{

MessageBox.Show("Начало диапазона должно быть меньше конца диапазона !");

return;

}

stopwatch.Start();

for (decimal i = start2.Value; i <= end2.Value; i++)

{

if (IsPrime2(Convert.ToInt32(i)))

{

listBox2.Items.Add(i);

}

}

stopwatch.Stop();

label9.Text = "Время выполнения: " + stopwatch.ElapsedMilliseconds + "мсек.";

}

Экранная форма метода представлена на Рисунке 8.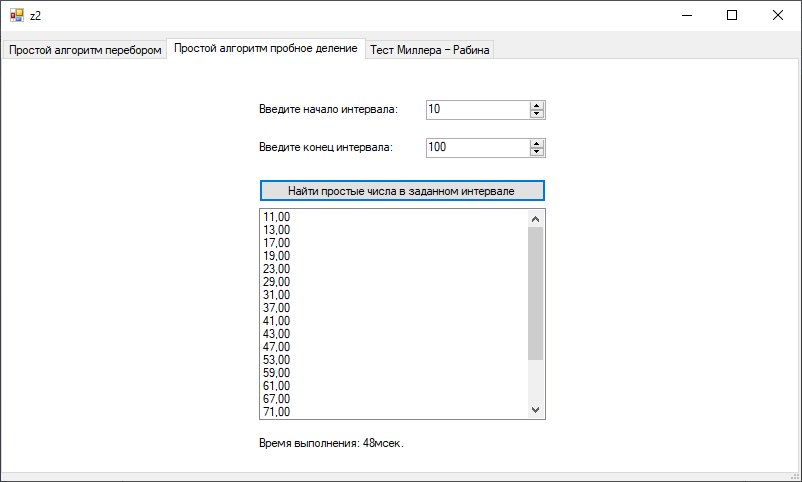



Рисунок 8. Экранная форма метода пробного деления

3. Тест Миллера-Рабина

Листинг:

public bool MillerRabinTest(BigInteger n, int k)

{

// если n == 2 или n == 3 - эти числа простые, возвращаем true

if (n == 2 || n == 3)

return true;

// если n < 2 или n четное - возвращаем false

if (n < 2 || n % 2 == 0)

return false;

// представим n − 1 в виде (2^s)·t, где t нечётно, это можно сделать последовательным делением n - 1 на 2

BigInteger t = n - 1;
int s = 0;
while (t % 2 == 0)

{

t /= 2;

s += 1;

}

// повторить k раз

for (int i = 0; i < k; i++)

{

// выберем случайное целое число a в отрезке [2, n − 2]

RNGCryptoServiceProvider rng = new RNGCryptoServiceProvider();

byte[] _a = new byte[n.ToByteArray().LongLength];

BigInteger a;

do

{

rng.GetBytes(_a);

a = new BigInteger(_a);

}

while (a < 2 || a >= n - 2);

// x ← a^t mod n, вычислим с помощью возведения в степень по модулю

BigInteger x = BigInteger.ModPow(a, t, n);

// если x == 1 или x == n − 1, то перейти на следующую итерацию цикла

if (x == 1 || x == n - 1)

continue;

// повторить s − 1 раз

for (int r = 1; r < s; r++)

{

// x ← x^2 mod n

x = BigInteger.ModPow(x, 2, n);

// если x == 1, то вернуть "составное"

if (x == 1)

return false;

// если x == n − 1, то перейти на следующую итерацию внешнего цикла

if (x == n - 1)

break;

}

if (x != n - 1)

return false;

}

// вернуть "вероятно простое"

return true;

}

private void button3_Click(object sender, EventArgs e)

{

listBox3.Items.Clear();

if (raund.Value < 1)

{

MessageBox.Show("Kоличество раундов проверки должно быть больше 0.");

return;

}

stopwatch.Start();

for (decimal i = start2.Value; i <= end2.Value; i++)

{

if (MillerRabinTest((BigInteger)i, Convert.ToInt32(raund.Value)))

{

listBox3.Items.Add(i);

}

}

stopwatch.Stop();

label10.Text = "Время выполнения: " + stopwatch.ElapsedMilliseconds + "мсек.";

}

Экранная форма метода представлена на Рисунке 9.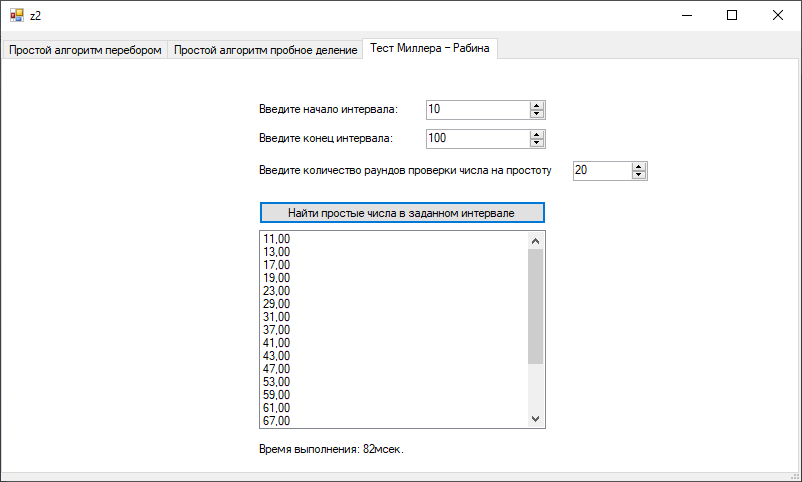



Рисунок 9. Экранная форма Тест Миллера-Рабина

3. Поиск пар чисел близнецов

Листинг:

using System;

using System.Collections.Generic;

using System.ComponentModel;

using System.Data;

using System.Drawing;

using System.Linq;

using System.Text;

using System.Threading.Tasks;

using System.Windows.Forms;

using System.Diagnostics;

namespace KR

{

public partial class z3 : Form

{

Stopwatch stopwatch = new Stopwatch();

public z3()

{

InitializeComponent();

}

static bool IsSimple(int n)

{

if (n < 2)

return false;

for (int i = 2; i <= n / 2; i++)

if (n % i == 0)

return false;

return true;

}

private void button1_Click(object sender, EventArgs e)

{

if (start1.Value >= end1.Value)

{

listBox1.Items.Clear();

MessageBox.Show("Начало диапазона должно быть меньше конца диапазона !");

return;

}

List items = new List();

stopwatch.Start();

for (int i = Convert.ToInt32(start1.Value); i < Convert.ToInt32(end1.Value); i++)

if (IsSimple(i))

items.Add(i);

listBox1.Items.Clear();

listBox1.Items.Add("Найдены простые числа:");

listBox1.Items.Add(string.Join(" ",items));

listBox1.Items.Add("Найдены пары чисел-близнецов:");

for (int i = 0; i < items.Count; i++)

{

for (int j = i + 1; j < items.Count; j++)

{

if (Math.Abs(items[i] - items[j]) == 2)

listBox1.Items.Add(items[i] + " " + items[j]);

}

}

stopwatch.Stop();

label4.Text = "Время выполнения: " + stopwatch.ElapsedMilliseconds + "мсек.";

panel1.Visible = true;

}

private void button2_Click(object sender, EventArgs e)

{
}

private void button2_Click_1(object sender, EventArgs e)

{

if (textBox1.Text == "")

{

MessageBox.Show("Не задано имя файла !");

return;

}

System.IO.StreamWriter SaveFile = new System.IO.StreamWriter(textBox1.Text);

foreach (var item in listBox1.Items)

{

SaveFile.WriteLine(item);

}

SaveFile.Close();

MessageBox.Show("Данные сохранены в файл.");

panel1.Visible = false;

}

private void textBox1_Enter(object sender, EventArgs e)

{

if (saveFileDialog1.ShowDialog() == DialogResult.Cancel)

return;

textBox1.Text = saveFileDialog1.FileName;

}

}

}

Экранная форма метода представлена на Рисунке 10.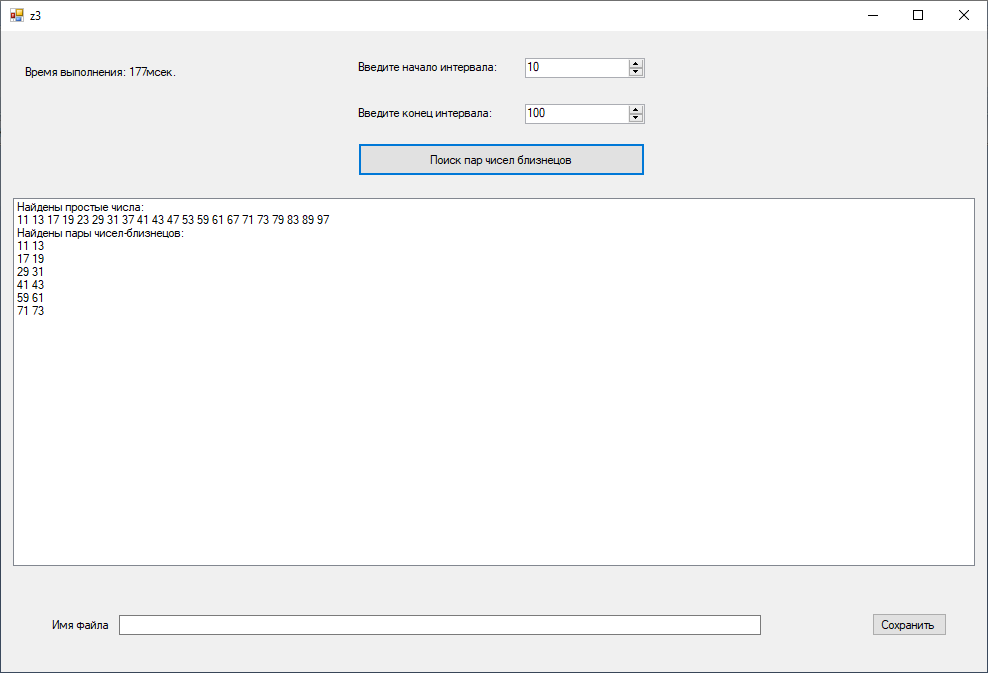



Рисунок 10. Экранная форма поиска чисел-близнецов

4. Разложение на простые множители

Листинг:

using System;

using System.Collections.Generic;

using System.ComponentModel;

using System.Data;

using System.Drawing;

using System.Linq;

using System.Text;

using System.Threading.Tasks;

using System.Windows.Forms;

using System.Diagnostics;

namespace KR

{

public partial class z4 : Form

{

Stopwatch stopwatch = new Stopwatch();

public z4()

{

InitializeComponent();

}

static List TrialDivision(uint n)

{

var divides = new List();

var div = 2u;

while (n % div == 0)

{

divides.Add(div);

n /= div;

}

div = 3;

while (Math.Pow(div, 2) <= n)

{

if (n % div == 0)

{

divides.Add(div);

n /= div;

}

else

{

div += 2;

}

}
if (n > 1)

{

divides.Add(n);

}

return divides;

}

private void button1_Click(object sender, EventArgs e)

{

listBox1.Items.Clear();

string res = Convert.ToString(numericUpDown1.Value)+" = ";

//foreach (var friend in TrialDivision(Convert.ToUInt32(numericUpDown1.Value)))

//{

// res = res + " "

//}

//listBox1.Items.Add(friend);

stopwatch.Start();

listBox1.Items.Add(Convert.ToString(numericUpDown1.Value) + " = " + string.Join(" * ", TrialDivision(Convert.ToUInt32(numericUpDown1.Value))));

stopwatch.Stop();

label2.Text = "Время выполнения: " + stopwatch.ElapsedMilliseconds + "мсек.";

panel1.Visible = true;

}

private void button2_Click(object sender, EventArgs e)

{

if (textBox1.Text == "")

{

MessageBox.Show("Не задано имя файла !");

return;

}

System.IO.StreamWriter SaveFile = new System.IO.StreamWriter(textBox1.Text);

foreach (var item in listBox1.Items)

{

SaveFile.WriteLine(item);

}

SaveFile.Close();

MessageBox.Show("Данные сохранены в файл.");

panel1.Visible = false;

}

private void textBox1_Enter(object sender, EventArgs e)

{

if (saveFileDialog1.ShowDialog() == DialogResult.Cancel)

return;

textBox1.Text = saveFileDialog1.FileName;

}

}

}

Экранная форма метода представлена на Рисунке 11.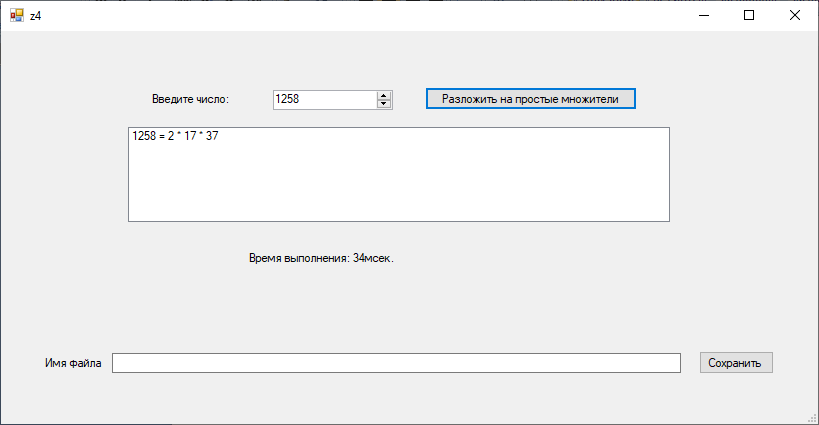



Рисунок 11. Экранная форма разложения на простые множители

ЗАКЛЮЧЕНИЕ

В ходе выполнения работы были изучены различные алгоритмы поиска простых чисел:

• 
  Простого перебора;
  
• 
  Пробного деления;
  
• 
  Тест Миллера – Рабина.
  

Так же были изучены метод «Поиск пар чисел близнецов» и «Разложение числа на простые множители».

По результатам изучение теоретических сведений, разработано приложение с графическим интерфейсом на языке программирования С#, реализующее эти алгоритмы.

Список литературы

1. 
   Мартин Гарднер. Математические головоломки иразвлечения. М.:Оникс, 1994.
   
2. 
   Глейзер Г.И. История математики в школе. М.:Просвещение,1982
   
3. 
   Л.Ф.Пичурин. За страницами учебника алгебры. М.:Просвещение,1991.
   
4. 
   Савин А.П. Энциклопедический словарь юного математика. М.:Педагогика,1989.
   
5. 
   Р.Курант, Г.Роббинс. Что такое математика? М.:МЦНМО, 2004.
   
6. 
   Карпенко А.С.: Логики Лукасевича и простые числа. - М.: Наука, 2000
   
7. 
   Гальперин Г. Просто о простых числах // Квант, 1987. – №4. С. 9-14.
   
8. 
   Мир математики: в 40 т. Т.2: Жуан Гомес. Математики, шпионы и хакеры. Кодирование и криптография. / Пер. с англ. – М.: Де Агостини, 2014. – 144 с.
   
9. 
   Мир математики: в 40 т. Т.3: Грисан Энрике. Простые числа. Долгая дорога к бесконечности. / Пер. с англ. – М.: Де Агостини, 2014с144 с.
   
10. 
    Росанова К. А., Воронцова Я. О., Гаврилова А. М., Шмелева О. В. Эти сложные простые числа! // Юный ученый. — 2016. — №6.1. — С. 40-41.