Алгоритмизации

• Название: Алгоритмизации
• Дата: 27.09.2022
• Размер: 1.15 Mb.
• Имя файла: 12_100229_1_124427 (1).docx
• Тип: Документы; #700459
• страница: 3 из 67

ГЛАВА 1. Введение в алгоритмы

1. ЭтапырешениязадачнаЭВМ

Условно программированиемможно назвать научную и практическую деятельность по созданию программ. Основной частью программирования является процесс решения задачи на ЭВМ, который можно разбить на следующие этапы:

1. 
   математическая или информационная формулировка задачи;
   
2. 
   выбор численного или иного метода решения поставленной задачи;
   
3. 
   построение алгоритма решения поставленной задачи;
   
4. 
   выбор языка программирования и запись построенного алгоритма по его правилам, т.е. написание текста программы;
   
5. 
   отладка программы – это процесс обнаружения, локализации и устранения возможных ошибок;
   
6. 
   выполнение программы, т.е. получение требуемого результата.
   

Рассмотрим более подробно некоторые наиболее важные из приведенных этапов.

2. Понятиеалгоритма

Понятие алгоритма занимает центральное место в современной математике и программировании.

Алгоритмизация – сведение задачи к последовательным этапам действий так, что результаты предыдущих действий используются при выполнении последующих.

Рассмотрим вначале некоторые наиболее важные (фундаментальные)

понятия программирования.

1. 
   Действие– это некоторая операция, имеющая конкретную продолжительность и приводящая к совершенно конкретному результату.
   
2. 
   Каждое действие предполагает наличие некоторых данных, над которыми это действие совершается и по изменению состояния которых определяют результат этого действия.
   
3. 
   Каждое действие должно быть таким, чтобы его можно было описать при помощи какого-либо языка (или набора формул); такое описание называют инструкция.
   
4. 
   Если действие можно разложить на составные части, то его называют процессом (или вычислением).
   
5. 
   Описание характера проведения процесса, т.е. последовательности выполняемых действий без привязки к какому-то конкретному процессору, называют алгоритмом.
   

Числовойалгоритм– детально описанный способ преобразования числовых входных данных в выходные при помощи математических операций. Существуют нечисловые алгоритмы, которые используются в экономике, технике и научных исследованиях.

В общем, алгоритм – строгий и четкий набор правил, определяющий последовательность действий, приводящих к достижению поставленной цели.

3. Свойстваалгоритмов

Дискретность – значения новых величин (данных) вычисляются по определенным правилам из других величин с уже известными значениями.

Определенность(детерминированность) – каждое правило из набора однозначно, а сами данные однозначно связаны между собой, т.е. последовательность действий алгоритма строго и точно определена.

Результативность(конечность) – алгоритм решает поставленную задачу за конечное число шагов.

Массовость– алгоритм разрабатывается так, чтобы его можно было применить для целого класса задач, например, алгоритм вычисления определенных интегралов с заданной точностью.

4. Сложностьалгоритма

Выполнение любого алгоритма требует определенного объема памяти компьютера для размещения данных и программы, а также времени по обработке этих данных – эти ресурсы ограничены и, следовательно, правомочен вопрос об эффективности их использования. Таким образом, в самом широком смысле понятие эффективности связано со всеми вычислительными ресурсами, необходимыми для работы алгоритма.

Однако обычно под «самымэффективным»понимается алгоритм, обеспечивающий наиболее быстрое получение результата, поэтому рассмотрим именно временнýю сложность алгоритмов.

Время работы алгоритма удобно выражать в виде функции от одной переменной, характеризующей «размер» конкретной задачи, т.е. объем входных данных, необходимых для ее решения. Тогда сравнительная сложность задач и может оцениваться через ее размер.

Поскольку описание задачи, предназначенной для решения посредством вычислительного устройства, можно рассматривать в виде слова конечной длины, представленной символами конечного алфавита, в качестве формальной характеристики размера задачи можно принять длину входного слова. Например, если стоит задача определения максимального числа в некоторой последовательности из n элементов, то и размер задачи будетn, поскольку любой вариант входной последовательности можно задать словом из n символов.

Временнаясложностьалгоритма – это функция, которая каждой входной длине слова n ставит в соответствие максимальное(для всех конкретных задач длиной n) время, затрачиваемое алгоритмом на ее решение.

Различные алгоритмы имеют различную временную сложность и выяснение того, какие из них окажутся достаточноэффективны, а какие

нет, определяется многими факторами. Однако для сравнения эффективности алгоритмов был предложен простой подход, позволяющий прояснить ситуацию. Речь идет о различии между полиномиальными и экспоненциальными алгоритмами.

Полиномиальнымназывается алгоритм, временнàя сложность которого выражается некоторой полиномиальной функцией размера задачи n.

Алгоритмы, временнáя сложность которых не поддается подобной оценке, называются экспоненциальными.

Задача считается труднорешаемой, если для нее не удается построить полиномиального алгоритма. Это утверждение не является категорическим, поскольку известны задачи, в которых достаточно эффективно работают и экспоненциальные алгоритмы. Примером может служить симплекс-метод, который успешно используется при решении задач линейного программирования, имея функцию сложности f(n) =2 ⁿ. Однако подобных примеров не очень много, и общей следует признать ситуацию, когда эффективно исполняемыми можно считать полиномиальные алгоритмы с функциями сложности n, n² или n³.

Например, при решении задачи поиска нужного элемента из n имеющихся в худшем варианте сложность равна n; если же оценить среднюю трудоемкость (продолжительность поиска), то она составит (n+1)/2 – в обоих случаях функция сложности оказывается линейнойn.

Сложность задачи вычисления определителя системы nлинейных уравнений сn неизвестными характеризуется полиномом 3-й степени. Повышение быстродействия элементов компьютера уменьшает время исполнения алгоритма, но не уменьшает степень полинома сложности.

5. Способыописанияалгоритмов

Существует несколько способов описания алгоритмов. Наиболее распространенные способы – это словесное и графическое описания алгоритма.

Словесноеописаниеалгоритма

В любом алгоритме для обозначения данных используют некоторый набор символов, называемыхбуквами. Конечную совокупность букв называют алфавитом, из любой конечной последовательности которого можно составить слово, т.е. в любом алфавите реальным данным можно сопоставить некоторые слова, в дальнейшем обозначающие эти данные.

При словесной записи алгоритм описывается с помощью естественного языка с использованием следующих конструкций:

1. 
   шаг (этап) обработки (вычисления) значений данных – «=»;
   
2. 
   проверка логического условия: если (условие) истинно, то выполнить действие 1, иначе – действие2;
   
3. 
   переход (передача управления) к определенному шагу (этапу) N.
   

Для примера рассмотрим алгоритм решения квадратного уравнения видаa�x²+b�x+c = 0:

1. 
   ввод исходных данных a, b, c(a,b,c≠ 0);
   
2. 
   вычислить дискриминант D= b² – 4�a�c;
   
3. 
   если D< 0, то перейти к п. 6, сообщив, что действительных корней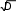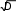
   

нет;

4. 
   иначе, еслиD≥ 0, вычислить х₁= (–b+ 5) вывести результаты х₁ и х₂ ;
   

6. 
   конец.
   

)/(2�a) и
₂х= (–b–
)/(2�a);

Графическоеописаниеалгоритма

Графическое изображение алгоритма – это представление его в виде схемы, состоящей из последовательности блоков (геометрических фигур), каждый из которых отображает содержание очередного шага алгоритма. А внутри фигур кратко записывают действие, выполняемое в этом блоке.

Такую схему называют блок-схемой или структурной схемой алгоритма, или просто схемой алгоритма.

Правила изображения фигур сведены в единую систему программной документации (дата введения последнего стандарта ГОСТ 19.701.90 – 01.01.1992).

По данному ГОСТу графическое изображение алгоритма – это схема данных, которая отображает путь данных при решении задачи и определяет этапы их обработки.

Схема данных состоит из следующих элементов:

• 
  символов данных (символы данных могут отображать вид носителя данных);
  
• 
  символов процесса, который нужно выполнить над данными;
  
• 
  символов линий, указывающих потоки данных между процессами и носителями данных;
  
• 
  специальных символов, которые используют для облегчения чтения схемы алгоритма.
  

Рассмотрим основные символы для изображения схемы алгоритма.

Символыввода-выводаданных:

• 
  данные ввода-вывода, если носитель не определен;
  

• 
  ручной ввод с устройства любого типа, например с клавиатуры;
  
• 
  отображение данных в удобочитаемой форме на устройстве, например дисплее.
  

Символыпроцесса:

• 
  
  А = 5
  процесс– отображение функции обработки данных, т.е. опе- рации, приводящей к изменению указанного значения;
  

–предопределенный процесс– отображение группы операций, которые определены в другом месте, например в подпрограмме (функции);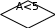

• 
  решение – отображение функции, имеющей один вход и ряд альтернативных выходов, из которых только один может быть активизирован после анализа условия, указанного внутри этого символа.
  

Символылиний– отображают поток данных или управления. Линии – горизонтальные или вертикальные, имеющие только прямой угол перегиба. Стрелки – указатели направления не ставятся, если управление идет сверху вниз или слева направо.

Специальныесимволы

Соединитель – используется при обрыве линии и продолжении ее в другом месте (необходимо присвоить название).
Терминатор– вход из внешней среды или выход во внешнюю среду (начало или конец схемы программы).

Комментарий.

6. Способыреализацииалгоритмов

Любую программу можно разбить на блоки, реализованные в виде алгоритмов (процессов), которые можно разделить на три вида:

1. 
   линейные (единственное направление выполнения);
   
2. 
   разветвляющиеся (направление выполнения определяет условие);
   
3. 
   циклические (отдельные участки вычислений выполняются многократно).
   

Любой циклический процесс включает в себя участок с разветвлением и может быть простым и сложным (вложенным).

Для решения вопроса о том, сколько раз нужно выполнить цикл, используется анализ переменной, которую называют параметром цикла.

Циклический процесс, в котором количество повторений заранее известно, называется циклом по счетчику, а циклический процесс, в котором количество повторений заранее неизвестно и зависит от получаемого в ходе вычислений результата, называют итерационным.

7. Примерпростейшеголинейногопроцесса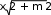

Наиболее часто в практике программирования требуется организовать расчет некоторого арифметического выражения при различных исходных данных. Например, такого:

tg² x

z=
_{+ x}(m+1) _,

гдеx> 0 – вещественное, m– целое.

Разработка алгоритма обычно начинается с составления схемы.

Продумывается оптимальная последовательность вычислений, при которой, например, отсутствуют повторения. При написании алгоритма рекомендуется переменным присваивать те же имена, которые фигурируют в заданном арифметическом выражении либо иллюстрируют их смысл.

Для того чтобы не было «длинных» операторов, исходное выражение полезно разбить на ряд более простых. В нашей задаче предлагается схема вычислений, представленная на рис. 1.1.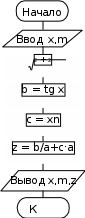





Рис. 1.1. Схема линейного процесса
Она содержит ввод и вывод исходных данных, линейный вычислительный процесс, вывод полученного результата. Заметим, что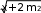

выражение вычисляется только один раз. Введя дополнительные

переменные a, b, c, мы разбили сложное выражение на ряд более простых.

1.7.Примерциклическогопроцесса

Вычислить значение функции y = sin x, представленной в виде разложения в ряд, с заданной точностью, т.е. до тех пор, пока разность между соседними слагаемыми не станет меньше заданной точности:

_x3

ysin x=−x+−+.

3!

_x5_x7


5! 7!

...

Схема алгоритма, приведенная на рис. 1.2, реализует циклический процесс, в состав которого (в блоке проверки |E|< eps) входит участок разветвления.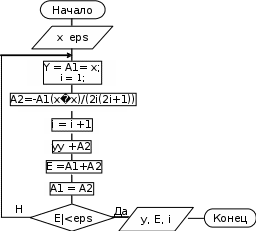




Рис. 1.2. Схема циклического алгоритма