Аналитический способ
 Скачать 127.05 Kb. Скачать 127.05 Kb.
|
|
1. Функцией называется закон, по которому числу х из заданного множества Х, поставлено в соответствие только одно число у, пишут , при этом x называют аргументом функции, y называют значением функции. 1) Аналитический способ. Аналитический способ - это наиболее часто встречающийся способ задания функции. Заключается он в том, что функция задается формулой, устанавливающей, какие операции нужно произвести над х, чтобы найти у. Функция может быть задана на разных частях множества X разными функциями. Например: Во всех ранее приведенных примерах аналитического способа задания, функция была задана явно. То есть, справа стояла переменная y, а слева формула от переменной х. Однако, при аналитическом способе задания, функция может быть задана и неявно. При аналитическом способе задания, функция может быть задана параметрически - это, когда х и у выражены через некоторый параметр t. 2) Графический способ. При графическом способе вводится прямоугольная система координат и в этой системе координат изображается множество точек с координатами (x,y). При этом Не всякое множество точек координатной плоскости, даже не всякая линия может служить графиком функции. Линия только в том случае задаёт функцию, если любая прямая, параллельная оси 0y, пересекает её не более чем в одной точке. 4. Табличный способ. Табличный способ наиболее удобен, когда множество Х конечно. При этом способе составляется таблица, в которой каждому элементу из множества Х, ставится в соответствие число Y. Недостатком табличного способа задания функции является то, что в таблице могут быть указаны лишь отдельные значения аргумента и функции. Особенности изменения функции при этом могут быть искажены или утрачены. 2. Множество чисел Число Если Это определение означает, что a есть предел числовой последовательности, если её общий член неограниченно приближается к a при возрастании n. Геометрически это значит, что для любого Последовательность называется ограниченной, если существует такое число M, что | un | Есть несколько типов числовых последовательностей, которые вы обязательно должны знать: 1) Возрастающая последовательность – каждый ее член больше предыдущего 2) Неубывающая последовательность – каждый следующий член не меньший от предыдущего 3) Нисходящая последовательность – каждый новый член меньше предыдущего 4) Невозрастающая последовательность – каждый старший член не больше предыдущего 5) Ограниченная последовательность имеет место тогда, когда найдутся такие действительные числа 6) Последовательность 7) Последовательность, имеющая предел называется сходящейся. Противоположная к ней последовательность - соответственно расходящимися. 3. Основные свойства пределов.Нижеприведенные свойства пределов справедливы не только для числовых последовательностей, но и для функций. Если { un } и { vn } две сходящиеся последовательности, то: 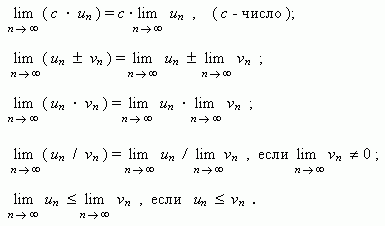 Если члены последовательностей { un}, { vn},{ wn}удовлетворяют неравенствам Некоторые замечательные пределы. 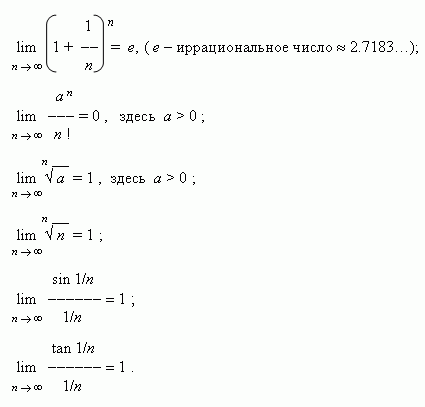 4. Теоремы о пределах Теорема 1. Если в точке а существуют пределы функций f(x) и g(x), то в этой точке существует и предел суммы f(x)±g(x),причём Теорема 2. Если в точке а существуют пределы функций f (x) и g (x), то существует и предел произведения f(x)×g(х), причем Следствие 1. Постоянный множитель можно выносить за знак предела. Действительно, Следствие 2. Теорема 3. Если в точке а существуют пределы функций f(х) и g (x) и при этом 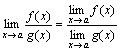 . .Теорема 4. Если функция f (x) имеет предел в точке а, отличный от нуля, то функция Докажем для примера, что Пусть Так как Тогда f (x) ± g(x) = [A + a(x)] ± [В + b(x)] = (А ± В) + (a(x) ± b(x)), где a(x) ± b(x) ® 0 при x ® a как алгебраическая сумма бесконечно малых a(x) и b(x). Таким образом, функция f (x) ± g(x) отличается от числа А ± В на бесконечно малую и, следовательно, это число является пределом суммы функций f(x) и g(x), то есть имеем Отметим, что при вычислении пределов сформулированные выше теоремы о пределах, как правило, не "работают", а попытка их применения приводит в итоге к неопределенности того или иного вида. Например, 5. 1)Замечательный тригонометрический предел (первый) Доказательство 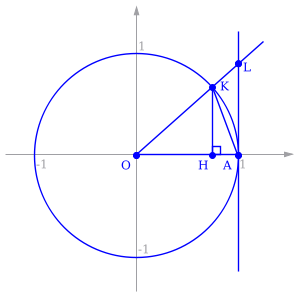 Рассмотрим односторонние пределы Пусть Точка K— точка пересечения луча с окружностью, а точкаL— с касательной к единичной окружности в точке (1;0). ТочкаH— проекция точкиKна осьOX. Очевидно, что: (где SsectOKA— площадь сектораOKA) (из Подставляя в (1), получим: Так как при Умножаем на sinx: Перейдём к пределу: Найдём левый односторонний предел: 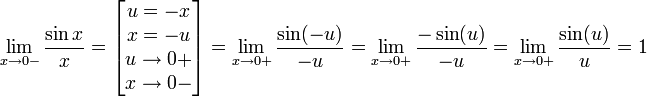 Правый и левый односторонний пределы существуют и равны 1, а значит и сам предел равен 1. Следствия Доказательство следствий 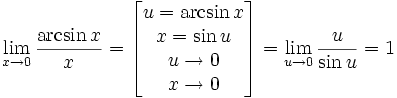 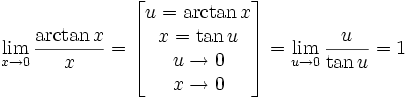 2) Замечательный показательно-степенной предел (второй) Следствия Доказательство следствия 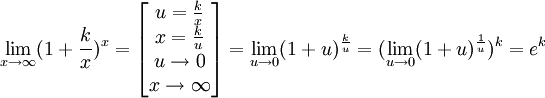 3) Замечательный логарифмический предел Доказательство предела Второе доказательство 4) Замечательный показательный предел Следствия Доказательство предела 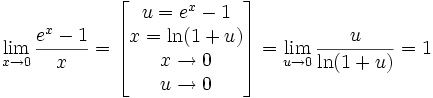 Ещё одно доказательство предела Доказательство следствия 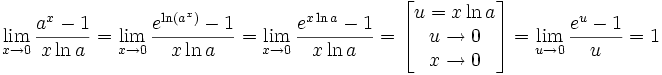 5) Замечательный степенной предел Доказательство предела |
