курсовая. Анализ методов кодирования данных Автор Анна Евкова

• Название: Анализ методов кодирования данных Автор Анна Евкова
• Дата: 13.05.2023
• Размер: 1.42 Mb.
• Имя файла: курсовая .docx
• Тип: Анализ; #1127096
• страница: 2 из 3

Глава 2.Кодирование информации в системе обработки информации 

2.1. Кодирование текстовой информации

В процессе обработки информации, т.е. преобразова­ния информации из одной формы представления (зна­ковой системы) в другую осуществляется кодирование. Средством кодирования служит таблица соответствия, которая устанавливает взаимно однозначное соответ­ствие между знаками или группами знаков двух раз­личных знаковых систем. При вводе знака алфавита в компьютер путем нажатия соответствующей клавиши на клави­атуре выполняется его кодирование, т. е. преобразо­вание в компьютерный код. При выводе знака на эк­ран монитора или принтер происходит обратный про­цесс — декодирование, когда из компьютерного кода знак преобразуется в графическое изображение.

Текст состоит из символов, поэтому символ можно считать минимальным элементом текста. Если собрать все возможные символы, которые могут встретиться в тексте: латинские буквы, буквы кириллицы, знаки пре­пинания и т. д., и каждому из этих символов присвоить свой уникальный номер (код символа), то текст можно записать в виде набора чисел.

Для хранения кода одного символа может быть вы­делен один байт. С помощью одного байта можно зако­дировать 256 различных символов, учитывая, что каж­дый бит принимает значение 0 или 1, и количество их возможных сочетаний в байте равно 2⁸=256. Этого вполне достаточно для представления текстовой инфор­мации, включая прописные и строчные буквы русского и латинского алфавитов, цифры, знаки, псевдографиче­ские символы и т. д [19, с.24].

Кодирование заключается в том, что каждому сим­волу ставится в соответствие уникальный десятичный код от 0 до 255 или соответствующий ему двоичный код от 00000000 до 11111111. Таким образом, человек разли­чает символы по их начертанию, а компьютер — по их коду. Важно, что присвоение символу конкретного ко­да — это вопрос соглашения, которое фиксируется в ко­довой таблице.

Технически это выглядит очень просто, однако всегда существовали достаточно веские организационные сложности. В первые годы развития вычислительной техники они были связаны с отсутствием необходимых стандартов, а в настоящее время вызваны, наоборот, изобилием одновременно действующих и противоречивых стандартов. Для того чтобы весь мир одинаково кодировал текстовые данные, нужны единые таблицы кодирования, а это пока невозможно из-за противоречий между символами национальных алфавитов, а также противоречий корпоративного характера.

Существует несколько различных стандартов коди­рования символов, но первоосновой для всех стал стандарт ASCII (American Standard Code for Information In­terchange — американский стандартный код для инфор­мационного обмена).

В ASCII закреплены две таблицы кодирования: ба­зовая и расширенная. В базовой таблице определены значения кодов с 0 по 127, а в расширенной — с 128 по 255. В базовой таблице находятся символы латинского алфавита, цифры, знаки арифметических операций и знаки препинания (табл. 1.1). Кроме того, за кодами с 0 по 32 закреплены специальные функции: перевод стро­ки, ввод пробела и т. д. Расширенная таблица содержит символы национальных алфавитов различных стран мира и так называемые символы псевдографики, с по­мощью которых можно, например, рисовать таблицы [19, с.25].



Рис.2.1 Таблица кодов ASCII (расширенная)

Для языков, использующих кириллицу, в том числе и для русского, пришлось полностью менять вторую полови­ну таблицы ASCII, приспосабливая её под кириллический алфавит. В частности, для представления символов ки­риллицы используется так называемая «альтернативная кодировка».

Альтернативная кодировка не подошла для ОС Windows. Пришлось передвинуть русские буквы в таб­лице на место псевдографики, и получили кодировку Windows 1251 (Win-1251). Кодировка символов русского языка, известная как кодировка Windows-1251, была введена «извне» - компанией Microsoft, но, учитывая широкое распространение операционных систем и других продуктов этой компании в России, она глубоко закрепилась и нашла широкое распространение.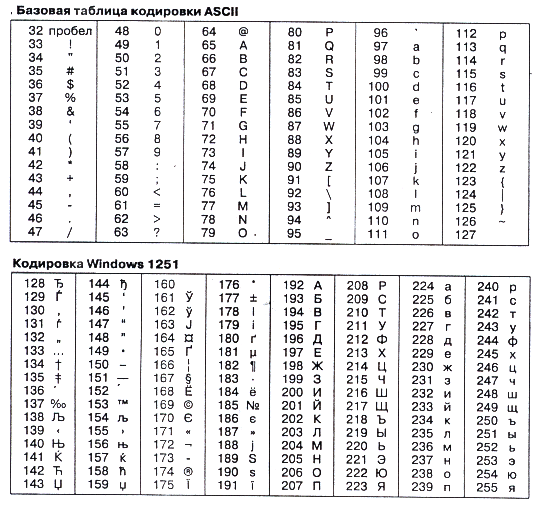



Сейчас существует несколько различных кодовых таблиц для русских букв (КОИ-8, СР-1251, СР-866, Мае, ISO), причём тексты, созданные в одной кодировке, мо­гут совершенно неправильно отображаться в другой. Решается такая проблема с помощью специальных про­грамм перевода текста из одной кодировки в другую [4. c.67].

Другая распространённая кодировка носит название КОИ-8 (код обмена информацией, восьмизначный) – её происхождение относится к временам действия Совета Экономической Взаимопомощи государств Восточной Европы. Сегодня кодировка КОИ – 8 имеет широкое распространение в компьютерных сетях на территории России и в российском секторе Интернета.

Международный стандарт, в котором предусмотрена кодировка символов русского языка, носит названия ISO (International Standard Organization – Международный институт стандартизации). На практике данная кодировка используется редко.

Если проанализировать организационные трудности, связанные с созданием единой системы кодирования текстовых данных, то можно прийти к выводу, что они вызваны ограниченным набором кодов (256). Математикам требуется использовать в формулах специальные математические знаки, переводчикам не­обходимо создавать тексты, где могут встретиться сим­волы из различных алфавитов, экономистам необходи­мы символы валют ($, F, А). Для решения этой проблемы была разработана универсальная система кодирования текстовой информации — UNICODE. В этой кодировке для каждого символа отводится не один, а два байта, то есть шестнадцать битов. Очевидно, что если, кодировать символы не восьмиразрядными двоичными числами, а числами с большим разрядом то и диапазон возможных значений кодов станет на много больше. Шестнадцать разрядов позволяют обеспечить уникальные коды для 65536 различных символов – этого поля вполне достаточно для размещения в одной таблице символов большинства языков планеты. Этого хватает на латинский алфавит, кириллицу, иврит, африканские и азиатские языки, раз­личные специализированные символы: математические, экономические, технические и многое другое.

Несмотря на тривиальную очевидность такого подхода, простой механический переход на данную систему долгое время сдерживался из-за недостатков ресурсов средств вычислительной техники (в системе кодирования UNICODE все текстовые документы становятся автоматически вдвое длиннее). Но во второй половине 90-х годов технические средства достигли необходимого уровня обеспечения ресурсами, и сегодня мы наблюдаем постепенный перевод документов и программных средств на универсальную систему кодирования UNICODE.

2.2. Кодирование целых и действительных чисел

Естественным представлением целого неотрицательного числа является двоичная система счисления. Кодирование отрицательных чисел производится тремя наиболее употребительными способами, в каждом из которых крайний левый бит - знаковый. Отрицательному числу соответствует единичный бит, а положительному - нулевой.

1. Прямой код. Изменение знака производится просто, путем инверсии бита знака. Пусть 00001001 = 9, тогда 10001001 = -9. Если при сложении двух чисел в этом коде знаки совпадают, то трудностей нет. Если знаки различаются необходимо найти наибольшее число, вычесть из него меньшее, а результату присвоить знак наибольшего слагаемого.

2. Обратный код, инверсный или дополнительный "до 1". Изменение знака производится просто - инверсией всех бит: 00001001 = 9, а 11110110 = - 9. Сложение также выполняется просто, т.к. знаковые биты можно складывать. При переносе единицы из левого (старшего) бита, она должна складываться с правым (младшим). Например: 7 + (-5) = 2.

00000111 = 7

11111010 =-5 (инверсия 00000101 = 5)

1 00000001

1

00000010 = 2

Сложение в обратном коде происходит быстрее, т.к. не требуется принятие решения, как в предыдущем случае. Однако суммирование бита переноса требует дополнительных действий. Другим недостатком этого кода является представление нуля двумя способами, т.к. инверсия 0...00 равна 1...11 и сумма двух разных по знаку, но равных по значению чисел дает 1...11. Например: (00001001 = 9) + (11110110 = -9) = 11111111. Кстати, из этого примера понятно, почему код называется дополнительным "до 1". Этих недостатков лишен код, дополнительный до 2.

3. Дополнительный или дополнительный "до 2" код. Число с противоположным знаком находится инверсией исходного и добавлением к результату единицы. Например, найти код числа -9.

00001001 = 9 11110111 =-9

11110110 - инверсия 00001000 - инверсия

1 1

11110111 =-9 00001001 = 9

Проблемы двух нулей нет. +0 = 00000000, -0 = 11111111 + 1 = 00000000 (перенос из старшего бита не учитывается).Сложение производится по обычным для неотрицательных чисел правилам.

00001001 = 9

11110111 =-9

1 00000000

Из этого примера видно, что в каждом разряде двух равных по модулю чисел складываются две единицы, что и определило название способа. Этот метод применяется наиболее часто, и когда говорят о дополнительном коде, то имеется в виду дополнительный "до 2-х" код.

Примеры однобайтных целых чисел:

D7	D6	D5	D4		D3	D2	D1	D0	Целое двоичное без знака (256 чисел)
S	D6	D5	D4		D3	D2	D1	D0	Целое двоичное co знаком (от ‑27 до
									+(27‑1)
D3	D2	D1	D0		D3	D2	D1	D0	Десятичное двоично-кодированное
старшая цифра				младшая цифра					(упакованный формат)

Числа с плавающей точкой. Вещественные числа хранятся в показательной форме, т.е. в виде двух составляющих: мантиссы и порядка. Различия в способах такого представления чисел заключаются в количестве байтов, отводимых под порядок и мантиссу и небольших отличиях в форме их хранения. Например в четырехбайтовом формате под мантиссу отводится 3 байта и один байт для хранения порядка (КВ - короткий вещественный формат):

Пример одного из вариантов формата:

байт 3

байт 2

байт 1

байт 0

s

s

порядок

мантисса (от 2-1 до 1)

Старший разряд старшего байта хранит знак мантиссы, следующий за ним - знак порядка.

В другом варианте знак мантиссы может храниться в старшем разряде байта 2, а сам порядок храниться в "смещенной" форме, в виде числа Е‑127.

Тогда представление числа D: D = ±M * 2^(E-127), где мантисса, Е – смещенный порядок, хранящийся в старшем байте. При этом может быть принято соглашение о неявном присутствии единицы слева от десятичной точки, так что мантисса будет принимать значения от 1 до 2. Соответственно в зависимости от вариаций формата будут слегка отличаться и диапазоны представления чисел. Так, в последнем варианте, где у нормализованной мантиссы первая значащая цифра (единица) мысленно находится слева от запятой, а справа располагаются 23 разряда - 1,xx..xx, Mmax = 1,111..11 = 1 +1/2 +1/4+ 1/8 +...= 2, а Mmin= 1,000..00 = 1 для положительных чисел (SM=0) и -1 и -2 для отрицательных, (SM=1). Порядок числа Emax = 11111110 = 254, а Emin = 00000001 = 1. Теперь можно определить диапазон представления положительных чисел от +Dmax = Mmax * 2(254-127) = 3,4 * 1038 до +Dmin = Mmin * 2(1-127) = 1,17 * 10-38. Точность определяется числом достоверных десятичных цифр. При 23 двоичных разрядах мантиссы 223 примерно равно 107, т.е. достоверными являются только 6-7 значащих десятичных знаков, а не 38. Необходимо отметить, что значения порядка 11111111 и 00000000 по международным стандартам IEEE 754 и IEEE 854 предназначены для кодирования денормализованных чисел, отрицательной и положительной бесконечностей, неопределенности и так называемых "Не-чисел" [7, c.89].

Целые числа кодируются двоичным кодом достаточно просто - необходимо взять целое число и делить его пополам до тех пор, пока частное не будет равно единице. Совокупность остатков от каждого деления, записанная справа налево вместе с последним частным, и образует двоичный аналог десятичного числа.

Для кодирования целых чисел от 0 до 255 достаточно иметь 8 разрядов двоичного кода (8 бит). 16 бит позволяют закодировать целые числа от 0 до 65535, а 24 – уже более 16,5 миллионов различных значений.

Для кодирования действительных чисел используют 80-разрядное кодирование. При этом число предварительно преобразовывают в нормализованную форму:

3,1414926 = 0,31415926  101

300 000 = 0,3  106

Первая часть числа называется мантиссой, а вторая – характеристикой. Большую часть из 80 бит отводят для хранения мантиссы (вместе со знаком) и некоторое фиксированное количество разрядов отводят для хранения характеристики.

2.3. Кодирование графических данных

Телевизионный способ представления видеоинфор­мации во многом повлиял на формирование принципов представления графической информации в компьютере. Одной из основополагающих идей телевидения является создание изображения на базе системы точек, «обегае­мых» по очереди, например, электронным лучом. Подоб­ную систему точек принято называть растром. Посмот­рев через лупу на экран телевизора или на фотографию, вы увидите множество точек различных цветов, состав­ляющих растр (см. рис. 1.1).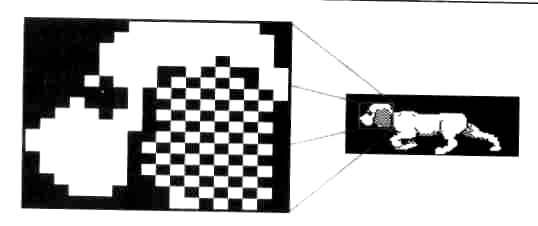



Рис. 2.2. Растровое изображение под увеличением

 Поскольку линейные координаты и индивидуальные свойства каждой точки (яркость) можно выразить с помощью целых чисел, то можно сказать, что растровое кодирование позволяет использовать двоичный код для представления графических данных. Закодировав каждый цвет каким-нибудь числом, можно представить изображение в виде последователь­ности чисел. Для чёрно-белого изображения на каждую точку будет достаточно одного бита: белый цвет будет обо­значаться единицей, а чёрный — нулём, как показано на рисунке 1.2.

Рис. 2.3. Цифровое представление чёрно-белого изображения

Общепринятым на сегодняшний день считается представление чёрно-белых иллюстраций в виде комбинации точек с 256 градациями серого цвета, и, таким образом, для кодирования яркости любой точки обычно достаточно восьмиразрядного двоичного числа.

Когда изображение включает оттенки серого цвета, требуется кодиро­вать каждый оттенок цве­та. Очевидно, что чем больше число оттенков, тем большее количество битов необходимо на каж­дую точку изображения. Справедлива общая фор­мула

N = 2ⁱ,

где N есть число цветов, а i — необ­ходимое количество битов информации [19, c. 27].

Например, для кодирования 256 градаций серого потребуется 8 битов, то есть 1 байт. В этом случае 0 будет означать чёрный цвет, 255 — белый, а числа от 1 до 254 — серые цвета различной яркости.

Цветные изображения кодируются сложнее. Часто при кодировании цвета используют трёхбайтовое кодирование, когда каждый байт представляет собой интен­сивность одного из трёх базовых цветов — красного, зе­лёного и синего. Это связано с природной цветовой чув­ствительностью глаза человека. Практически любой цвет, воспринимаемый глазом, можно получить, смеши­вая три этих базовых цвета. Например, пурпурный цвет получается от смешения красного и синего, а жёл­тый — от смешения красного и зелёного. Меняя пропор­ции, можно получить различные оттенки. Если смешать все три базовых цвета в одинаковой пропорции, то полу­чится серый цвет. Такой способ кодирования цвета на­зывается RGB (Red, Green, Blue).

Если яркость каждого из базовых цветов кодировать числом от 0 до 255, то потребуется 3 байта (то есть 24 бита) на каждую точку. В этом случае белый цвет бу­дет кодироваться тремя числами (255,255, 255), чёр­ный — (0, 0, 0). Коды (255, 255, 200) будут обозначать блёкло-жёлтый цвет, а (100, 0, 100) — тёмно-фиолетовый.

Режим представления цветной графики с использованием 24 двоичных разрядов называется полноцветным (True Color).

Каждому из основных цветов можно поставить в соответствие дополнительный цвет, т.е. цвет, дополняющий основной цвет до белого. Нетрудно заметить, что для любого из основных цветов дополнительным будет цвет, образованный суммой пары остальных основных цветов. Соответственно дополнительными цветами являются: голубой (Cyan), пурпурный (Magenta) и жёлтый (Yellow). Принцип декомпозиции произвольного цвета на составляющие компоненты можно применять не только для основных цветов, но и для дополнительных, т.е. любой цвет можно представить в виде суммы голубой, пурпурной и жёлтой составляющей. Такой метод кодирования цвета принят в полиграфии, но в полиграфии используется ещё и четвёртая краска – чёрная (Black). Поэтому данная система кодирования обозначается четырьмя буквами CMYK (чёрный цвет обозначается буквой К, потому, что буква В уже занята синим цветом), и для представления цветной графики в этой системе надо иметь 32 двоичных разряда. Такой режим также называется полноцветным.

Если уменьшить количество двоичных разрядов, используемых для кодирования цвета каждой точки, то можно сократить объём данных, но при этом диапазон кодируемых цветов заметно сокращается. Кодирование цветной графики 16-разрядными двоичными числами называется режимом High Color.

Отдельный элемент графического изображения имеет широко распространённое название — пиксель (от англ. picture element — элемент изображения). Чем гу­ще сетка пикселей на мониторе, тем лучше качество изображения. Размер графической сетки обычно пред­ставляется в форме произведения числа точек в гори­зонтальной строке на число строк: MxN. Мы можем настраивать режим работы монитора, например: 800x600 или 1024x768 пикселей.

По существу, кодирование цветов отдельных пиксе­лей аналогично кодированию символов текста. Таблица нумерации цветов есть своеобразный алфавит, пользу­ясь которым, компьютер записывает графическую ин­формацию. В итоге, как и в случае с текстом, получается последовательность целых чисел, которая стандартным образом сохраняется в памяти.

С практической точки зрения очень важно понимать, что количество используемых на рисунке цветов сущест­венным образом сказывается на размере графического файла. Для записи чёрно-белого изображения, имеющего 100 точек по вертикали и 100 точек по горизонтали, по­требуется 100x100 = 10000 битов (1250 байтов). Изобра­жение такого же размера, но использующее 256 града­ций серого цвета, потребует 100 х 100 х 8 = 80 000 битов (10000 байтов). Изображение, использующее 24-битный код, потребует:

100x100x24 = 240 000 битов (30 000 байтов).

2.4. Кодирование звуковой информации

Информация, в том числе графическая и звуковая, может быть пред­ставлена в аналоговой или дискретной форме. При аналоговом представлении физическая величина при­нимает бесконечное множество значений, причем ее значения изменяются непрерывно. При дискретном представлении физическая величина принимает ко­нечное множество значений, причем ее величина изме­няется скачкообразно. Примером аналогового представления графической информации может служить, скажем, живописное по­лотно, цвет которого изменяется непрерывно, а дис­кретного — изображение, напечатанное с помощью струйного принтера и состоящее из отдельных точек разного цвета. Примером аналогового хранения звуковой инфор­мации является виниловая пластинка (звуковая до­рожка изменяет свою форму непрерывно), а дискрет­ного — аудиокомпакт-диск (звуковая дорожка которого содержит участки с различной отражающей способностью). Звуковая информация из аналоговой формы в дискретную преобразуется путем дискрети­зации, т.е. разбиения непрерывного (аналогового) звукового сигнала на отдельные элементы. В процессе дискретиза­ции производится кодирование, т. е. присвоение каждо­му элементу конкретного значения в форме кода.

Дискретизация — это преобразование непрерыв­ных изображений и звука в набор дискретных значе­ний, каждому из которых присваивается значение его кода.

Как известно из курса физики, звук — это колебания среды, непрерывный сигнал с меняющейся амплитудой (рис. 1.3).



Рис.2.4. Звуковая волна

При кодировании звука этот сигнал надо предста­вить в виде последовательности нулей и единиц. Как, например, это происходит в микрофоне? Через равные промежутки времени, очень часто (десятки тысяч раз в секунду) измеряется амплитуда колебаний. Каждое из­мерение производится с ограниченной точностью и запи­сывается в двоичном виде. Частота, с которой записыва­ется амплитуда, называется частотой дискретизации [19. c. 29].

Полученный ступенчатый сигнал сначала сглаживается посредством аналогового фильтра, а затем преобразует­ся в звук с помощью усилителя и динамика.

На качество воспроизведения закодированного звука в основном влияют два параметра: частота дискретиза­ции— количество измерений амплитуды за секунду в герцах и глубина кодирования звука — размер в битах, отводимый под запись значения амплитуды.

Например, при записи на компакт-диски (CD) используются 16-разрядные значения, а частота дискретизации равна 44 032 Гц. Эти параметры обеспечивают превосходное качество звучания речи и музыки. Для стереозвука отдельно записывают данные для левого и для правого канала.

Приёмы и методы работы со звуковой информацией пришли в вычислительную технику наиболее поздно. К тому же, в отличие от числовых, текстовых и графических данных, у звукозаписей не было столь же длительной и проверенной истории кодирования. В итоге методы кодирования звуковой информации двоичным кодом далеки от стандартизации. Множество отдельных компаний разработали свои корпоративные стандарты, но среди них можно выделить два основных направления [6. c. 115].

1. Метод FM (Frequency Modulation) основан та том, что теоретически любой сложный звук можно разложить на последовательность простейших гармонических сигналов разных частот, каждый из которых представляет собой правильную синусоиду, а, следовательно, может быть описан числовыми параметрами, т.е. кодом. В природе звуковые сигналы имеют непрерывный спектр, т.е. являются аналоговыми. Их разложение в гармонические ряды и представление в виде дискретных цифровых сигналов выполняют специальный устройства – аналогово-цифровые преобразователи (АЦП). Обратное преобразование для воспроизведения звука, закодированного числовым кодом, выполняют цифро-аналоговые преобразователи (ЦАП). При таких преобразованиях неизбежны потери информации, связанные с методом кодирования, поэтому качество звукозаписи обычно получается не вполне удовлетворительным и соответствует качеству звучания простейших электромузыкальных инструментов с окрасом характерным для электронной музыки. В то же время данный метод копирования обеспечивает весьма компактный код, поэтому он нашёл применение ещё в те годы, когда ресурсы средств вычислительной техники были явно недостаточны.

2. Метод таблично волнового (Wave-Table) синтеза лучше соответствует современному уровню развития техники. В заранее подготовленных таблицах хранятся образцы звуков для множества различных музыкальных инструментах. В технике такие образцы называют сэмплами. Числовые коды выражают тип инструмента, номер его модели, высоту тона, продолжительность и интенсивность звука, динамику его изменения, некоторые параметры среды, в которой происходит звучание, а также прочие параметры, характеризующие особенности звучания. Поскольку в качестве образцов исполняются реальные звуки, то его качество получается очень высоким и приближается к качеству звучания реальных музыкальных инструментов.