курсовая. Анализ методов кодирования данных Автор Анна Евкова
 Скачать 1.42 Mb. Скачать 1.42 Mb.
|
     / Курсовые работы / Анализ методов кодирования данных  Автор Анна Евкова Преподаватель который помогает студентам и школьникам в учёбе. Анализ методов кодирования данных Содержание: Введение Глава 1. Сущность кодирования информации 1.1. Основные определения кодирования. Алфавит кодирования 1.2 Кодирование информации с помощью систем счисления Глава 2.Кодирование информации в системе обработки информации 2.1. Кодирование текстовой информации 2.2. Кодирование целых и действительных чисел 2.3. Кодирование графических данных 2.4. Кодирование звуковой информации Заключение Список использованной литературы  Введение Актуальность темы. К концу XX в. стала складываться, сначала в рамках кибернетики, а затем информатики, информационная картина мира. Строение и функционирование сложных систем различной природы (биологических, социальных, технических) оказалось невозможным объяснить, не рассматривая общих закономерностей информационных процессов. Автоматизированная система обработки информации (АСОИ) представляет собой совокупность информации, экономико-математических методов и моделей, технических, программных, технологических средств и штата специалистов, предназначенную для обработки информации и принятия управленческих решений По мере развития и усложнения средств, методов и форм автоматизации процессов обработки информации повышается зависимость общества от степени безопасности используемых им информационных технологий, от которых порой зависит благополучие, а иногда и жизнь многих людей. Здесь необходимо введение каких-либо мер по защите информации от несанкционированного доступа к ним, такой мерой можно считать кодирование. Во всех его формах и видах представления. Целью исследования курсовой работы является изучение методов кодирования данных. В связи с поставленной целью курсовой работы, были определенный следующие задачи: Рассмотреть основные определения кодирования. Алфавит кодирования; Изучить способ кодирование информации с помощью систем счисления; Охарактеризовать способы кодирования текстовой информации; Выявить способы кодирования целых и действительных чисел; Рассмотреть кодирование графических данных; Проследить особенности кодирования звуковой информации. Объектом исследования курсовой работы является система кодирования данных. Предметом исследования курсовой работы являются методы и приемы кодирования данных. Структура курсовой работы. Курсовая работа состоит из введения, двух глав, разделенных на параграфы, заключения и списка литературы. Глава 1. Сущность кодирования информации 1.1. Основные определения кодирования. Алфавит кодирования Для автоматизации работы с данными, относящимися к различным типам очень важно унифицировать их форму представления. Для этого обычно используется приём кодирования, т.е. выражение данных одного типа через данные другого типа. Существует множество понятий и определений «кода». Но мы в своей работе будем опираться на следующее: «Код (code) – это совокупность знаков, символов и правил представления информации».[10, с.40] В частности можно различать двоичный и троичный код. Алфавит первого ограничен двумя символами (0, 1), а второго – тремя символами (-1, 0, +1). Сигналы, реализующие коды, обладают одной из следующих характеристик: униполярный код (значения сигнала равны 0, +1, либо 0, -1 ); полярный код (значения сигнала равны +1, -1); биполярный код (значения сигнала равны 0, +1, -1). Кодируемые элементы входного алфавита обычно называют символами. Символом, как правило, является цифра, буква, знак пунктуации или иероглиф естественного языка, знак препинания, знак пробела, специальный знак, символ операции. Кроме того, учитываются управляющие («непечатные») символы. Кодирующие (обозначающие) элементы выходного алфавита называются знаками; количество различных знаков в выходном алфавите назовем значностью; количество знаков в кодирующей последовательности для одного символа – разрядностью кода. Последовательным является такой код, в котором знаки следуют один за другим во времени. Параллельным – тот, в котором знаки передаются одновременно, образуя символ. [10, с.41] Естественные человеческие языки – системы кодирования понятий для выражения мыслей посредством речи. К языкам близко примыкают азбуки – системы кодирования компонентов языка с помощью графических символов. Естественные языки обладают большой избыточностью для экономии памяти, объем которой ограничен, имеет смысл ликвидировать избыточность текста или уплотнить текст. Существуют несколько способов уплотнения текста. 1. Переход от естественных обозначений к более компактным. Этот способ применяется для сжатия записи дат, номеров изделий, уличных адресов и т.д. Идея способа показана на примере сжатия записи даты. Обычно мы записываем дату в виде 10. 05. 01. , что требует 6 байтов памяти ЭВМ. Однако ясно, что для представления дня достаточно 5 битов, месяца - 4, года - не более 7, т.е. вся дата может быть записана в 16 битах или в 2-х байтах. 2. Подавление повторяющихся символов. В различных информационных текстах часто встречаются цепочки повторяющихся символов, например пробелы или нули в числовых полях. Если имеется группа повторяющихся символов длиной более 3, то ее длину можно сократить до трех символов. Сжатая таким образом группа повторяющихся символов представляет собой триграф S P N , в котором S – символ повторения; P – признак повторения; N- количество символов повторения, закодированных в триграфе. В других схемах подавления повторяющихся символов используют особенность кодов ДКОИ, КОИ- 7, КОИ-8 , заключающуюся в том, что большинство допустимых в них битовых комбинаций не используется для представления символьных данных. 3. Кодирование часто используемых элементов данных. Этот способ уплотнения данных также основан на употреблении неиспользуемых комбинаций кода ДКОИ. Для кодирования, например, имен людей можно использовать комбинации из двух байтов диграф PN, где P – признак кодирования имени, N – номер имени. Таким образом может быть закодировано 256 имен людей, чего обычно бывает достаточно в информационных системах. Другой способ основан на отыскании в текстах наиболее часто встречающихся сочетании букв и даже слов и замене их на неиспользуемые байты кода ДКОИ. 4. Посимвольное кодирование. Семибитовые и восьмибитовые коды не обеспечивают достаточно компактного кодирования символьной информации. Более пригодными для этой цели являются 5 - битовые коды, например международный телеграфный код МГК-2. Перевод информации в код МГК-2 возможен с помощью программного перекодирования или с использованием специальных элементов на основе больших интегральных схем (БИС). Пропускная способность каналов связи при передаче алфавитно-цифровой информации в коде МГК-2 повышается по сравнению с использованием восьмибитовых кодов почти на 40%. 5. Коды переменной длины. Коды с переменным числом битов на символ позволяют добиться еще более плотной упаковки данных. Метод заключается в том, что часто используемые символы кодируются короткими кодами, а символы с низкой частотой использования - длинными кодами. Идея такого кодирования была впервые высказана Хаффманом, и соответствующий код называется кодом Хаффмана. Использование кодов Хаффмана позволяет достичь сокращения исходного текста почти на 80%. Использование различных методов уплотнения текстов кроме своего основного назначения – уменьшения информационной избыточности – обеспечивает определенную криптографическую обработку информации. Однако наибольшего эффекта можно достичь при совместном использовании как методов шифрования, так и методов кодирования информации [6, с.95]. Надежность защиты информации может быть оценена временем, которое требуется на расшифрование (разгадывание) информации и определение ключей. Если информация зашифрована с помощью простой подстановки, то расшифровать ее можно было бы, определив частоты появления каждой буквы в шифрованном тексте и сравнив их с частотами букв русского алфавита. Таким образом определяется подстановочный алфавит и расшифровывается текст. Информация передается в виде сообщений. Дискретная информация записывается с помощью некоторого конечного набора знаков, которые будем называть буквами, не вкладывая в это слово привычного ограниченного значения (типа «русские буквы» или «латинские буквы»). Буква в данном расширенном понимании - любой из знаков, которые некоторым соглашением установлены для общения. Например, при передаче сообщений на русском языке такими знаками будут русские буквы. Вообще, буквой будем называть элемент некоторого конечного множества (набора) отличных друг от друга знаков. Множество знаков, в котором определен их порядок, назовем алфавитом.[18, с.86] Рассмотрим некоторые примеры алфавитов. 1. Алфавит прописных русских букв: А Б В Г Д Е Ё Ж З И Й К Л М Н О П Р С Т У Ф Х Ц Ч Ш Щ Ъ Ы Ь Э Ю Я 2. Алфавит Морзе: 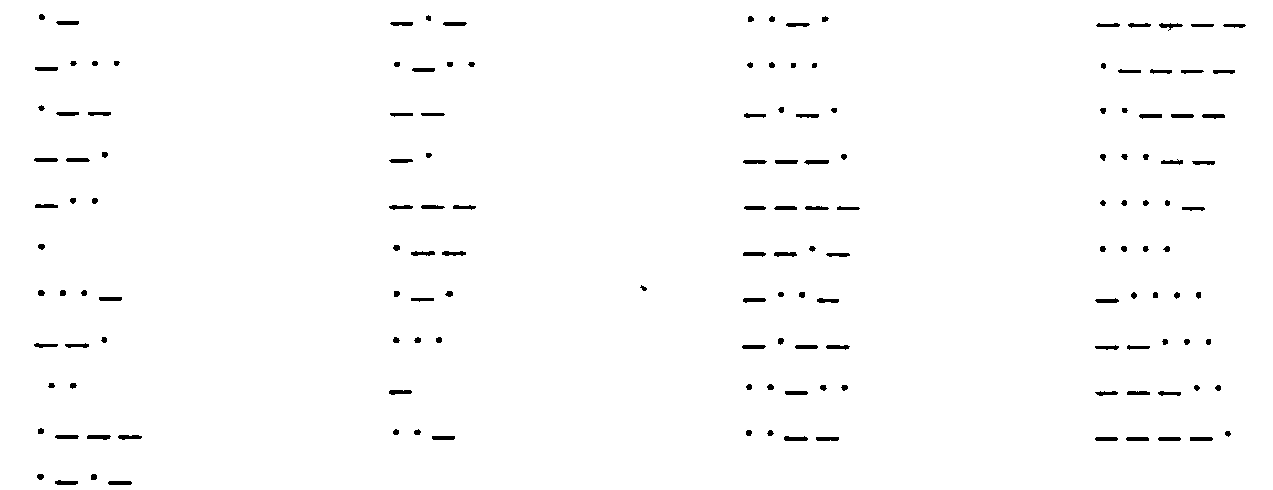 3. Алфавит клавиатурных символов ПЭВМ IBM (русифицированная клавиатура):  4. Алфавит знаков правильной шестигранной игральной кости:  5. Алфавит арабских цифр: 0123456789 6. Алфавит шестнадцатеричных цифр: 0123456789ABCDEF Этот пример, в частности, показывает, что знаки одного алфавита могут образовываться из знаков других алфавитов. 7. Алфавит двоичных цифр: 0 1 Алфавит 7 является одним из примеров, так называемых, «двоичных» алфавитов, т.е. алфавитов, состоящих из двух знаков. Другими примерами являются двоичные алфавиты 8 и 9: 8. Двоичный алфавит «точка», «тире»: . _ 9. Двоичный алфавит «плюс», «минус»: + - 10. Алфавит прописных латинских букв: ABCDEFGHIJKLMNOPQRSTUVWXYZ 11. Алфавит римской системы счисления: I V Х L С D М 12. Алфавит языка блок-схем изображения алгоритмов:  . .В канале связи сообщение, составленное из символов (букв) одного алфавита, может преобразовываться в сообщение из символов (букв) другого алфавита. Саму процедуру преобразования сообщения называют перекодировкой. Подобное преобразование сообщения может осуществляться в момент поступления сообщения от источника в канал связи (кодирование) и в момент приема сообщения получателем (декодирование). Устройства, обеспечивающие кодирование и декодирование, будем называть соответственно кодировщиком и декодировщиком. На рисунке приведена схема, иллюстрирующая процесс передачи сообщения в случае перекодировки, а также воздействия помех[3, с.11]. 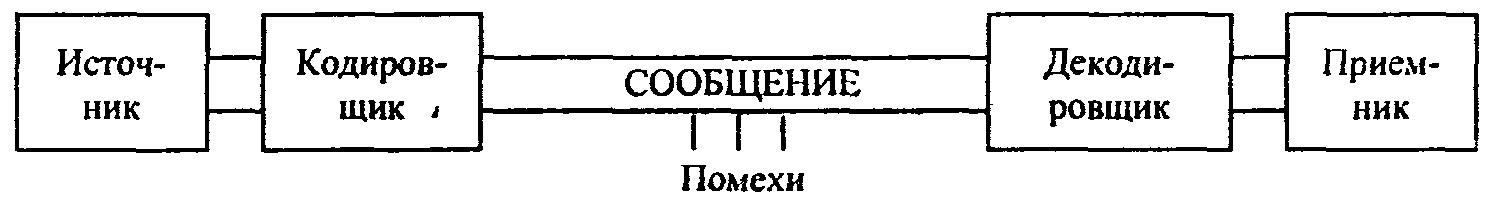 1.2 Кодирование информации с помощью систем счисления Для записи информации о количестве объектов используются числа. Числа записываются с использованием особых знаковых систем, которые называются системами счисления. Алфавит систем счисления состоит из символов, которые называются цифрами. Например, в десятичной системе счисления числа записываются с помощью десяти всем хорошо известных цифр: 0, 1, 2, 3, 4, 5, 6, 7, 8, 9. Система счисления — это знаковая система, в которой числа записываются по определенным правилам с помощью символов некоторого алфавита, называемых цифрами. [7, с.6] Все системы счисления делятся на две большие группы: позиционные и непозиционные системы счисления. Римская непозиционная система счисления. Самой распространенной из непозиционных систем счисления является римская. В качестве цифр в ней используются: I (1), V (5), X (10), L (50), С (100), D (500), М (1000). Значение цифры не зависит от ее положения в числе. Например, в числе XXX (30) цифра X встречается трижды и в каждом случае обозначает одну и ту же величину - число 10, три числа по 10 в сумме дают 30. Величина числа в римской системе счисления определяется как сумма или разность цифр в числе. Если меньшая цифра стоит слева от большей, то она вычитается, если справа — прибавляется. Например, запись десятичного числа 1998 в римской системе счисления будет выглядеть следующим образом: MCMXCVIII = 1000 + (1000 - 100) + (100 -10)+5 + 1 + 1 + 1. Позиционные системы счисления. Первая позиционная система счисления была придумана еще в Древнем Вавилоне, причем вавилонская нумерация была шестидесятеричной, то есть в ней использовалось шестьдесят цифр! Интересно, что до сих пор при измерении времени мы используем основание, равное 60 (в 1 минуте содержится 60 секунд, а в 1 часе — 60 минут). В XIX веке довольно широкое распространение получила двенадцатеричная система счисления. До сих пор мы часто употребляем дюжину (число 12): в сутках две дюжины часов, круг содержит тридцать дюжин градусов и так далее. В позиционных системах счисления количественное значение цифры зависит от ее позиции в числе. Наиболее распространенными в настоящее время позиционными системами счисления являются десятичная, двоичная, восьмеричная и шестнадцатеричная. Каждая позиционная система имеет определенный алфавит цифр и основание. В позиционных системах счисления основание системы равно количеству цифр (знаков в ее алфавите) и определяет, во сколько раз различаются значения одинаковых цифр, стоящих в соседних позициях числа. Десятичная система счисления имеет алфавит цифр, который состоит из десяти всем известных, так называемых арабских, цифр, и основание, равное 10, двоичная — две цифры и основание 2, восьмеричная — восемь цифр и основание 8, шестнадцатеричная — шестнадцать цифр (в качестве цифр используются и буквы латинского алфавита) и основание 16. 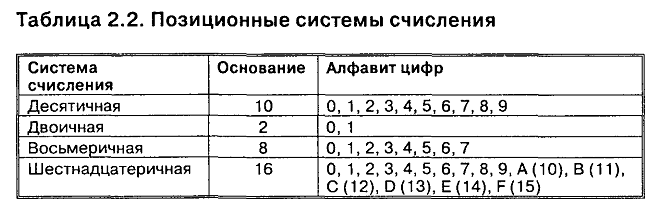 Таблица 1.1 Таблица 1.1Позиционные системы счисления Двоичная система счисления. В двоичной системе счисления основание равно 2, а алфавит состоит из двух цифр (0 и 1). Следовательно, числа в двоичной системе в развернутой форме записываются в виде суммы степеней основания 2 с коэффициентами, в качестве которых выступают цифры 0 или 1. [10, с.47] Любое неотрицательное число в позиционной системе счисления может быть представлено в виде:  , ,где а - основание системы счисления, хi - разряды (числа от 0 до а-1), их обозначения образуют алфавит системы счисления, аi - весовые коэффициенты (веса) разрядов, n - число разрядов целой части числа, р - число разрядов дробной части числа. Например, число в десятичной системе счисления 57310=5*102+7*101+3*100 Число в двоичной системе счисления:  Позиционная система счисления - такая, в которой весовые коэффициенты определяются позицией разряда. В вычислительной технике наиболее распространены: двоичная (binary, BIN), десятичная (decimal, DEC), шестнадцатеричная (hexadecimal, HEX) и непозиционная двоично-десятичная (binary coded decimal, BCD) системы исчисления. В BCD системе вес каждого разряда равен степени 10, как в десятичной системе, а каждая цифра i-го разряда кодируется 4-мя двоичными цифрами. Восьмеричная система счисления (octal, OCT) применяется реже. Следует отметить, что в цифровые устройства используют только двоичную систему счисления, так как построены на основе устройств с двумя состояниями. Другие системы счисления используются человеком только для удобства записи, т.е. для сокращенного (и часто более удобного) представления двоичных чисел. Формат двоичного числа
Микропроцессоры обрабатывают упорядоченные двоичные наборы. Минимальной единицей информации является один бит (BInary digiT). Далее следуют – тетрада, или ниббл (4 бита), байт ( byte, 8 бит), двойное слово (DoubleWord 16 бит) или длинное (LongWord 16 бит) и учетверенное (32 бита) слова. Младший бит обычно занимает крайнюю правую позицию, старший - соответственно крайнюю левую, т.е. “старшинство” разрядов убывает слева направо. Шестнадцатеричное представление двоичных чисел. Для перевода числа из двоичной системы в шестнадцатеричную, его необходимо разбить, начиная справа на тетрады - группы по 4 двоичных цифры - и каждую группу представить шестнадцатеричной цифрой из таблицы. Для обратного перевода каждая HEX цифра заменяется четверкой двоичных, незначащие нули слева иногда (но не всегда) отбрасываются. Нуль обычно не отбрасывается, если старший значащий знак обозначен буквой (см. таблицу). Таблица 1.2 Двоичные и шестнадцатиричные (HEX) коды целых чисел от 0 до 15
Пример: число 57310 = 10001111012 = 023D16 = 023Dh Вывод по 1 главе Для автоматизации работы с данными, относящимися к различным типам используется приём кодирования, т.е. выражение данных одного типа через данные другого типа. Мы в своей работе будем опираться на следующее определение: «Код (code) – это совокупность знаков, символов и правил представления информации». Сигналы, реализующие коды, обладают одной из следующих характеристик: униполярный код (значения сигнала равны 0, +1, либо 0, -1 ); полярный код (значения сигнала равны +1, -1); биполярный код (значения сигнала равны 0, +1, -1). Последовательным является такой код, в котором знаки следуют один за другим во времени. Параллельным – тот, в котором знаки передаются одновременно, образуя символ. Естественные языки обладают большой избыточностью, поэтому для экономии памяти, объем которой ограничен, имеет смысл ликвидировать избыточность текста или уплотнить текст. Существуют несколько способов уплотнения текста. Переход от естественных обозначений к более компактным. Подавление повторяющихся символов. Кодирование часто используемых элементов данных. Посимвольное кодирование. Коды переменной длины. Информация передается в виде сообщений. Дискретная информация записывается с помощью некоторого конечного набора знаков, которые называются буквами. Буква в данном расширенном понимании - любой из знаков, которые некоторым соглашением установлены для общения. В канале связи сообщение, составленное из символов (букв) одного алфавита, может преобразовываться в сообщение из символов (букв) другого алфавита. Саму процедуру преобразования сообщения называют перекодировкой. Для записи информации о количестве объектов используются числа. Числа записываются с использованием особых знаковых систем, которые называются системами счисления. Все системы счисления делятся на две большие группы: позиционные и непозиционные системы счисления. Самой распространенной из непозиционных систем счисления является римская. Наиболее распространенными в настоящее время позиционными системами счисления являются десятичная, двоичная, восьмеричная и шестнадцатеричная. Первая позиционная система счисления была придумана еще в Древнем Вавилоне, в XIX веке довольно широкое распространение получила двенадцатеричная система счисления. В настоящее время человечество приняло в использование десятеричную систему счисления. В позиционных системах счисления количественное значение цифры зависит от ее позиции в числе. Перевод из одной систему счисления в другую производится с помощью определенных правил, а в частности для двоичных, восьмеричных и шестнадцатеричных с использованием триад и тетрад, обеспечивающих удобство перевода. | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||

