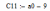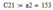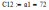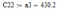ТАУ. Анализ непрерывной линейной сау
 Скачать 279.99 Kb. Скачать 279.99 Kb.
|
|
Министерство образования и высшего образования Российской Федерации Федеральное государственное бюджетное образовательное учреждение высшего образования «Пермский национальный исследовательский политехнический университет» Кафедра Микропроцессорных средств автоматизации. ОТЧЕТ
Пермь 2022 г Цель работы.Целью работы является овладение методикой расчета и способами измерения качества САУ. Исходные данныеДан объект – замкнутая одноконтурная система автоматического управления. 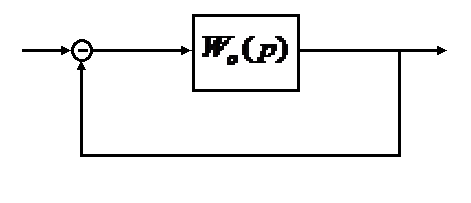 Передаточная функция разомкнутой части объекта – Численные значения параметров a, b, c, d указаны в таблице. Численное значение параметра 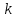 вычислено в ходе выполнения работы. вычислено в ходе выполнения работы.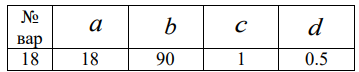 Значение параметра 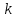 было вычислено в ходе выполнения работы. было вычислено в ходе выполнения работы.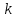 =0,3* =0,3*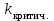 =0.3*1134=340.2 =0.3*1134=340.2 Таким образом, получаем передаточную функцию: 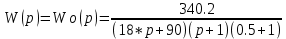 Порядок выполнения работы. Определить вид типовых звеньев, входящих в состав разомкнутой САУ. Пользуясь правилами преобразования схем, рассчитать передаточные функции разомкнутого контура системы W(p) и замкнутого контура Ф(p). Записать дифференциальное уравнение, описывающее замкнутую систему. Записать характеристическое уравнение D(p) для замкнутой системы. Получить условие устойчивости относительно величины параметра 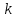 с помощью критерия Гурвица (определить с помощью критерия Гурвица (определить 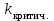 ). ).Задаться значением 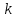 =0,3 =0,3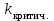 . .Доказать устойчивость замкнутой системы анализом значений корней характеристического уравнения. Доказать устойчивость замкнутой системы, используя критерий Рауса. Доказать устойчивость замкнутой системы, используя следствие из критерия Михайлова. Предложить возможный вид кривой Михайлова для исследуемой САУ (рисунок может иметь приблизительный характер), соответствующий теории. 11. Предложить возможный вид кривой Найквиста (рисунок может иметь приблизительный характер), соответствующий теории. 12. Определить основные показатели качества САУ косвенным (корневым) методом. 13. Рассчитать величину установившейся ошибки (для замкнутой системы) при подаче на вход единичного ступенчатого сигнала. 14. Построить асимптотическую логарифмическую амплитудно-частотную характеристику (ЛАЧХ) разомкнутой системы. 15. Получить описание исходной системы методом пространства состояния, используя метод прямого программирования). 16. Получить описание исходной системы методом пространства состояния, используя метод последовательного программирования. 17. Решить задачу на составление структурной функциональной схемы САУ, по вариантам:  Задание 1 Запишем передаточную функцию (ПФ) разомкнутой системы с учётом числовых коэффициентов и сведём ПФ к стандартному виду: 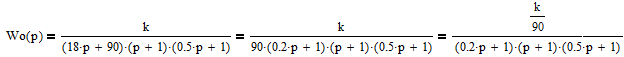 В состав разомкнутой системы входят: пропорциональное звено с коэффициентом передачи k/90, а также 3 апериодических звена 1 порядка с постоянными времени 0.2, 1 и 0.5 соответственно. Задание 2 Эквивалентная ПФ разомкнутой системы эквивалентна ПФ объекта: Тогда эквивалентная ПФ замкнутой системы, охваченной единичной отрицательной обратной связью: 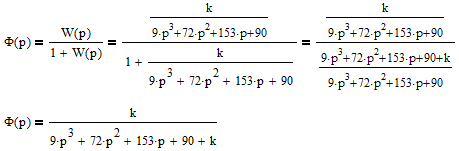 Задание 3 Запишем ПФ замкнутой системы, полагая Y выходным сигналом, а U входным сигналом: Тогда операторное уравнение системы: Перейдём от операторного уравнения к дифференциальному, произведя замену 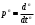 : :Задание 4 Характеристический полином замкнутой системы – это знаменатель ПФ замкнутой системы: Задание 5 В задании 4 мы определили характеристический полином замкнутой системы: По критерию Гурвица, система со всеми положительными коэффициентами находится на колебательной границе устойчивости, если последний и предпоследний определители матрицы равны нулю, а определители младших порядков положительные. Зная характеристический полином, формируем матрицу Гурвица по правилу: Из коэффициентов характеристического уравнения замкнутой системы a0pn + a1pn-1 + … + an = 0 составляется таблица, называемая матрицей Гурвица по следующему правилу: 1) по диагонали сверху вниз записываются все коэффициенты, начиная с a1 до an в порядке возрастания индексов; 2) столбцы дополняются вверх коэффициентами с возрастающими индексами, вниз коэффициентами с убывающими индексами; 3) на месте коэффициентов с индексами больше n и меньше нуля проставляются нули. Матрица Гурвица: 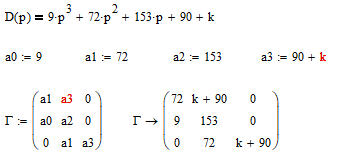 Рассчитываем определители матрицы Гурвица: 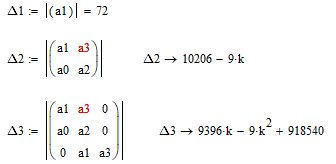 Приравняв 2 и 3 определители к нулю, определим, при каких k будет выполнено данное условие: 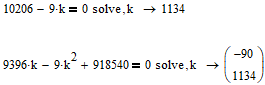 2 и 3 определители матрицы Гурвица обращаются в ноль при k = 1134; следовательно, данное значение и будет являться критическим значением k. Примечание k = -90, при котором 3 определитель обращается в ноль, соответствует апериодической границе устойчивости. Задание 6 Для дальнейших расчётов задаёмся значением: Задание 7 После выбора k = 340,2 характеристический полином будет иметь вид: По корневому критерию, система устойчива, если корни характеристического полинома имеют отрицательные вещественные части. Приравняв полином к нулю, находим корни с помощью пакета MathCAD: 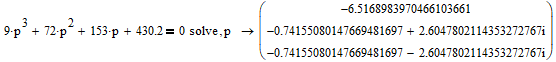 Все корни имеют отрицательную вещественную часть, следовательно, замкнутая система устойчива. Задание 8 Для проверки устойчивости по критерию Рауса выделяем характеристическое уравнение системы автоматического регулирования в виде: Число строк таблицы Рауса на единицу больше степени характеристического уравнения. Если при вычислении индекса получается отрицательное число, то соответствующий коэффициент равен нулю. Критерий устойчивости Рауса формулируется следующим образом. Для устойчивости замкнутой системы автоматического регулирования необходимо и достаточно, чтобы коэффициенты первого столбца таблицы Рауса были положительными, т.е. чтобы 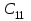 >0; >0; 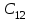 >0; …; >0; …;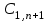 >0. Если при расчете в предпоследней строке первого столбца таблицы получится нуль, это значит, что система находится на границе устойчивости. >0. Если при расчете в предпоследней строке первого столбца таблицы получится нуль, это значит, что система находится на границе устойчивости.Заполняем таблицу Рауса: 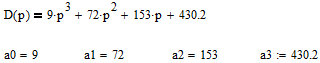
Все элементы I столбца таблицы Рауса положительные, следовательно, замкнутая система устойчива. Задание 9 Для расчёта устойчивости по критерию Михайлова, произведём в характеристическом полиноме замену p = i·ω, где i – мнимая единица; ω – частота: Выделяем вещественную и мнимую составляющую: Следствие из критерия Михайлова: система устойчива, если вещественная и мнимая части характеристической функции 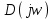 обращаются в нуль поочередно, т.е. если корни уравнений обращаются в нуль поочередно, т.е. если корни уравнений 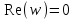 и и 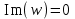 перемежаются и перемежаются и 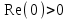 и и 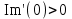 . .Найдём корни вещественной и мнимой составляющей. Примечание. Отрицательные частоты мы не исследуем. 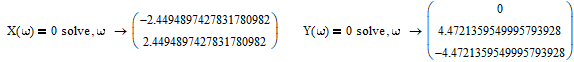 Корни перемежаются, следовательно, условие устойчивости выполняется. Задание 10 По частотному критерию Михайлова, система устойчива, если годограф Михайлова системы начинается на положительной полуоси, и раскручиваясь против часовой стрелки, последовательно проходит n четвертей (n – порядок характеристического полинома системы), не проходя через точку начала координат. Откладывая по оси абсцисс вещественную составляющую, а по оси ординат мнимую составляющую, найденные в задании 9, строим годограф Михайлова: 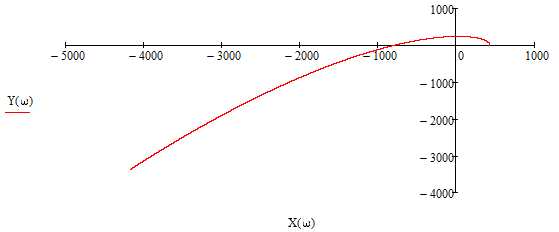 Годограф Михайлова системы начинается на положительной полуоси, и раскручиваясь против часовой стрелки, последовательно проходит n = 3 четверти, что соответствует поведению годографа устойчивой системы. Замкнутая система устойчива. Задание 11 Запишем ПФ разомкнутой системы с учётом выбранного значения коэффициента передачи k и сведём её к стандартной форме: [Примечание. Для дальнейших расчётов будет использоваться данная стандартная форма] Знаменатель разомкнутой системы представлен в виде произведения 3 множителей 1 порядка со всеми положительными коэффициентами, следовательно, разомкнутая система устойчива. Тогда, по критерию Найквиста, замкнутая система будет устойчива, если годограф АФЧХ (Найквиста) разомкнутой системы не будет охватывать точку (-1; i0). Годограф Найквиста разомкнутой системы: 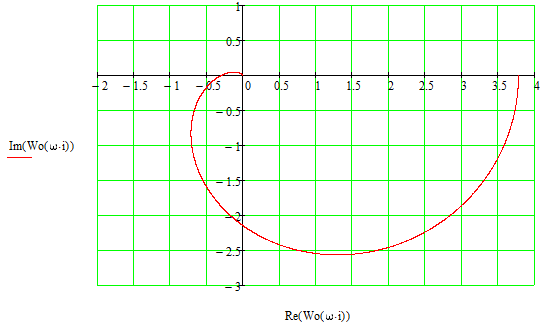 Задание 12 В задании 7 мы нашли корни характеристического полинома замкнутой системы: 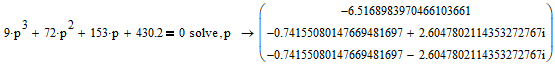 Поскольку все корни «левые», замкнутая система будет устойчива. Отметим также, что переходный процесс будет колебательным, т.к. в решении присутствуют комплексные корни. Основные показатели качества: Расстояние от мнимой оси до действительной части ближайшего к ней корня называется степенью устойчивости. В нашем случае, степень устойчивости составляет: Колебательные свойства системы регулирования предопределяет пара комплексных корней 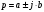 : : Приблизительное время регулирования: Перерегулирование не будет превышать: Задание 13 Запишем ПФ по ошибке канала управления: 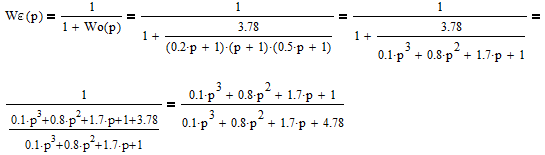 Установившаяся ошибка может быть найдена по формуле: 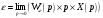 В этой формуле: Wε(p) – ПФ системы по ошибке p – оператор Лапласа 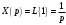 – изображение единичного ступенчатого сигнала по Лапласу – изображение единичного ступенчатого сигнала по ЛапласуТогда установившаяся ошибка: 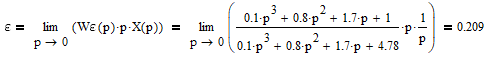 Задание 14 ПФ разомкнутой системы в стандартной форме: Определяем частоты перегиба: Т.к. все частоты принадлежат находящимся в знаменателе множителям вида Т·р+1, каждая частота будет давать излом в -20 дБ. В системе отсутствуют интегрирующие и дифференцирующие звенья (свободные множители р в числителе и знаменателе). Следовательно, низкочастотная асимптота ЛАЧХ будет идти под наклоном «0 дБ/дек» на уровне: L(ω) = 20·lg(K) = 20·lg(3,78) = 11,55 дБ. На частоте ω1 ЛАЧХ будет иметь излом и далее пойдёт под наклоном «-20 дБ/дек». На частоте ω2 ЛАЧХ будет иметь второй излом и далее пойдёт под наклоном «-40 дБ/дек». На частоте ω3 ЛАЧХ будет иметь третий излом и далее пойдёт под наклоном «-60 дБ/дек». 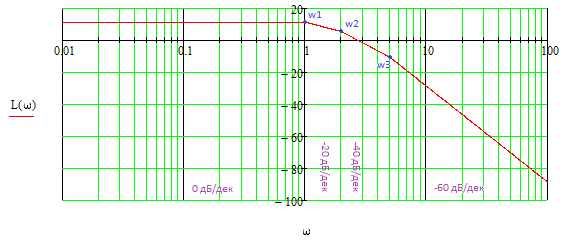 Задание 15 Построим систему в пространстве состояний, используя метод прямого программирования [1] ПФ разомкнутой системы: 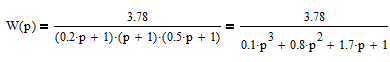 Разделим числитель и знаменатель на 0,1·р3: 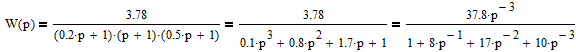 По полученным данным строим схему: 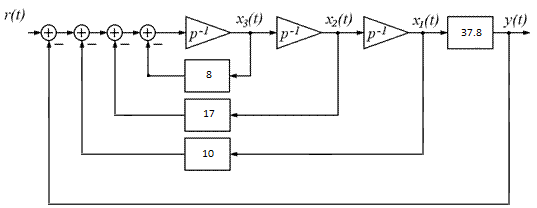 Задание 16 Построим систему в пространстве состояний, используя метод последовательного программирования [2] ПФ разомкнутой системы: 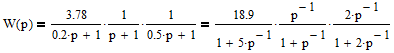 По полученным данным строим схему:  Задание 17 Входным параметром системы является плотность газа (воздуха) внутри шара pш. Выходным параметром системы является высота летательного аппарата h. Разность плотностей газа в шаре и вне него обеспечивает подъем на некоторую высоту h. Структурная схема системы. Структурная схема системы приведена на рис. 1. 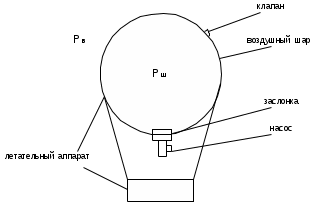 Рис.1. Она включает в себя: Устройство управления (заслонка+насос). Исполнительный механизм (собственно воздушный шар + клапан). Объект управления (летательный аппарат). Датчик высоты. Объект управления набирает высоту за счет разницы разности плотностей (давлений) в шаре и вне него. Следовательно, уравнение динамики летательного аппарата будет иметь вид: 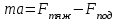 (1), (1),где 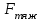 - это сила тяготения, равная - это сила тяготения, равная 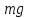 , а , а 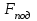 - подъемная сила (фактически Архимедова сила, равная произведению разницы плотностей, объема шара и ускорения свободного падения). - подъемная сила (фактически Архимедова сила, равная произведению разницы плотностей, объема шара и ускорения свободного падения).Функциональная схема устройства. Функциональная схема системы приведена на рис. 2.: 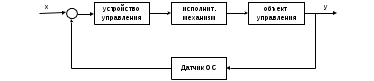 Передаточные функции звеньев системы. Устройство управления. УУ является идеальным усилительным звеном. 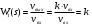 , где , где 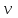 - скорость заполнения шара газом - скорость заполнения шара газом 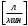 . .Исполнительный механизм. Исполнительный механизм (ИМ) – воздушный шар, имеющий клапан на своей оболочке. Взлет летательного аппарата осуществляется за счет наполнения воздухом шара. Когда процесс наполнения (увеличения плотности) достигает некоторого критического уровня, достаточного для подъема всего устройства, открывается клапан, поддерживающий величину плотности постоянной. Следовательно, процесс заполнения шара газом можно представить в виде выражения: 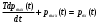 . (2) . (2)Осуществляя операторное преобразование Лапласа над выражением 2, получаем: 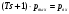 Тогда передаточная функция всего звена будет иметь вид: 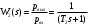 , т.е. ИМ – апериодическое звено. , т.е. ИМ – апериодическое звено.Объект управления. Поскольку, из второго закона Ньютона, наличие ускорения у тела (материальной точки) есть следствие приложенной к нему силы, и ускорение есть вторая производная перемещения (высоты ОУ h) по времени, то запишем: 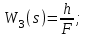 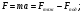 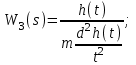 Осуществляя операторное преобразование Лапласа, получаем: 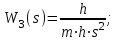 или, заменяя или, заменяя 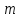 на на 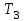 , ,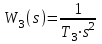 , т.е. ОУ – два последовательных интегрирующих звена. , т.е. ОУ – два последовательных интегрирующих звена.Датчик обратной связи. Датчик ОС считывает высоту ОУ нал поверхностью, никак не влияя на нее. поэтому вся система замкнута единичной обратной связью. 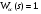 Список литературы [1] https://studfile.net/preview/2652091/page:27/ [2] https://studfile.net/preview/2652091/page:28/ |