ОБЖ. Анализ причин несчастных случаев на производстве
 Скачать 245.16 Kb. Скачать 245.16 Kb.
|
|
4. Анализ динамики несчастных случаев на производстве Для обобщающей характеристики травматизма на предприятии (в цехе) на  основе ряда динамики рассчитываются средние показатели: среднее число несчастных случаев за изучаемый период; средний абсолютный размер роста (или снижения) числа несчастных случаев и среднегодовой темп их роста (снижения) и прироста (снижения). основе ряда динамики рассчитываются средние показатели: среднее число несчастных случаев за изучаемый период; средний абсолютный размер роста (или снижения) числа несчастных случаев и среднегодовой темп их роста (снижения) и прироста (снижения).Среднее число несчастных случаев получим, если сложим все уровни ряда и разделим на их число, т. е. используем следующую формулу: где По данным табл. 3 среднее число несчастных случаев за 2006—2011 гг. составит: 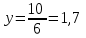 т. е. в среднем ежегодно за указанный период происходило 5 несчастных случаев. Средний абсолютный прирост (снижение) числа несчастных случаев за изучаемый период можно рассчитать по следующей формуле где По данным табл. 6 средний абсолютный прирост составит 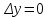 т. е. в среднем ежегодно число несчастных случаев за указанный период не изменялось. Для определения средней скорости изменения числа несчастных случаев за изучаемый период вычисляется средний темп роста. Среднегодовой темп роста (снижения) числа несчастных случаев можно рассчитать по следующей формуле где n — число членов динамического ряда; Для МСЦ-7 среднегодовой темп снижения числа несчастных случаев будет равен: Т=100% т.е. в среднем за изучаемый период число несчастных случаев не снижалось и не увеличивалось. Показатели динамики, рассмотренные для анализа абсолютного числа несчастных случаев, можно использовать также для анализа показателей частоты и тяжести несчастных случаев. 5. Изучение тенденции производственного травматизма и его прогноз Проведенный предварительный анализ не показывает четкой закономерности развития изучаемого показателя, так как в одни периоды возможно будет происходить снижение числа несчастных случаев, а в другие — их повышение и, таким образом, общая тенденция развития будет не ясна. Для выявления общей тенденции развития используются особые приемы обработки рядов динамики. Наиболее эффективным методом выявления основной тенденции развития является аналитическое выравнивание (определение тренда). В этом случае фактические уровни ряда заменяются уровнями, рассчитанными на основе определения кривой, при условии предположения, что она отражает общую тенденцию (тренд) изменения во времени. Для цели уровни ряда динамики выражаются в виде функции времени 5.1. Выравнивание по прямой линии Аналитическое уравнение прямой линии имеет вид где Для нахождения параметров уравнения  ,(9) ,(9)Аналитическое выравнивание можно существенно упростить соответствующим подбором значений tтак, чтобы 1. Если число членов динамического ряда нечетное, то t следует отсчитывать от середины ряда. При таком отчете значение серединной даты (или периода) динамического ряда принимается равным нулю, ранние даты имеют отрицательные значения (–1; –2; –3 и т. д.), а поздние даты — положительные значения (1; 2; 3 и т. д.). 2. Если число членов ряда четное, то и в этом случае сохранятся требования о равных интервалах между всеми значениями t и о том, чтобы сумма всех значений t равнялась нулю. Подбор значений t производится так: находится серединная пара дат (или периодов) и значения t для нее принимают: –1 и +1, а далее вверх идут –3; –5; – и т. д., и вниз +3; +5; +7 и т. д. В табл. 8 приведены все необходимые данные для решения системы (9). Упрощенная система уравнений примет вид:  , (10) , (10)Отсюда  (11) (11)Подставив численные значения в выражение (11), получим 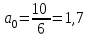 и и 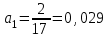 Подставим численные значения 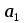 в уравнение прямой линии (8), получим в уравнение прямой линии (8), получим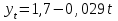 (12) (12)Данное уравнение показывает, что число несчастных случаев снижается в среднем на 0,029 случая в год, т. е. параметр Подставляя в уравнение (12) соответствующие значения t из табл. 8, получим теоретические значения числа несчастных случаев 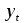 (координаты для построения прямой линии). (координаты для построения прямой линии).Для оценки правильности выбора уравнения используется среднеквадратическое отклонение фактических уровней ряда от уровней, вычисленных по уравнению тренда  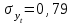 (13) (13)где n — число уровней ряда; р — число оцениваемых параметров в уравнении тренда ( 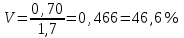 Таблица 8. Вспомогательная таблица для определения параметров прямой линии
Таким образом, Коэффициент вариации рассчитываем по формуле (14) Как видим, изменения довольно значительные. Это можно объяснить тем, что мы рассматривали короткий ряд динамики. 5.2. Прогноз травматизма до 2016 года Воспользуемся программой «Прогноз.ехе» и определим кривую. При этом надо помнить, что отдавать предпочтение той или иной модели тренда необходимо на основании глубокого качественного анализа изучаемого явления. Для ПСП-1 (см. табл. 6) распределение травматизма по годам и его прогноз на 5 лет наилучшим образом аппроксимируется кривой вида 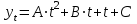 , (15) , (15)где А = 13694,87; В = 14200,39; С = –22239,77, p и q — коэффициенты перемасштабирования оси (автоматическое); x — год, в котором определяется число травм. Таблица 9. Вспомогательная таблица для расчета тренда
Аппроксимированная кривая имеет вид 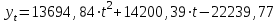 . .Для расчета 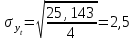 ; ; 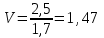 =14,7%. =14,7%.Значение коэффициента вариации V говорит о том, что аппроксимированная кривая несколько более точно воспроизводит фактические значения числа несчастных случаев, чем прямая линия. В табл. 10 дана сравнительная характеристика рассмотренных трендов. Как видно из нее, наилучшим образом требованию наименьших квадратов отвечает уравнение кривой. Таблица 10. Сравнительная характеристика уравнений тренда производственного травматизма
Прогноз числа несчастных случаев на основе других кривых выравнивания осуществляется аналогично. При составлении прогноза используют интервальную оценку, определяя для этого доверительные границы (интервалы) прогноза. Величины доверительных интервалов определяются по формуле где t — здесь критерий Стьюдента; Величина Определим доверительные интервалы прогноза по формуле (16). Для этого используем теоретические значения травматизма по кривой (15) до 2016 г. и фактические данные травматизма Фактические данные, линейная тенденция, рассчитанная по уравнению прямой линии и прогноз по уравнению (15), представлены на рис. 4. 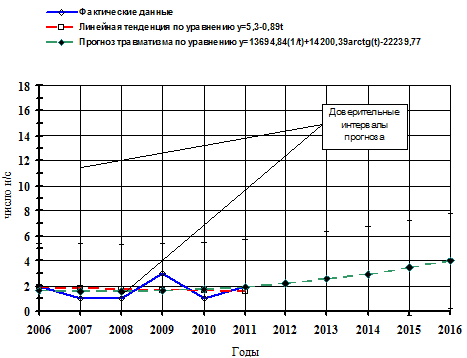 Рис. 4. Фактические данные, линейная тенденция, рассчитанная по уравнению прямой линии и его прогноз до 2016 г. |