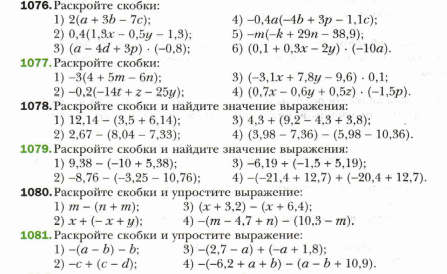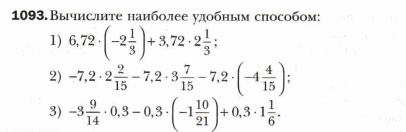Практическая работа № 3.
Проанализируйте содержание и методический аппарат УМК, преимущественно используемые в образовательных организациях муниципалитета, субъекта Российской Федерации, в контексте требований примерной рабочей программы по предмету.
Задание № 1. Заполните таблицу.
УМК (предмет, класс)
|
Содержание учебного материала
|
Наличие элементов содержания согласно ПРП
|
Отсутствующие элементы содержания согласно ПРП
|
УМК Колягин Ю.М. (алгебра, 7 класс)
|
Тема «Арифметические действия с рациональными числами» изложена в разделе «Алгебраические выражения». Тема «Степень с натуральным показателем на основе определения, запись больших чисел» в разделе «Одночлены и многочлены».
Алгебраические выражения. Переменные, числовое значение выражения с переменной. Допустимые значения переменных. Представление зависимости между величинами в виде формулы. Вычисления по формулам. Преобразование буквенных выражений, тождественно равные выражения, правила преобразования сумм и произведений, правила раскрытия скобок и приведения подобных слагаемых.
Следующее содержание согласно ПРП излагается в разделах «Одночлены и многочлены» и «Разложение многочленов на множители» данного УМК: Свойства степени с натуральным показателем. Одночлены и многочлены. Степень многочлена. Сложение, вычитание, умножение многочленов. Формулы сокращённого умножения: квадрат суммы и квадрат разности. Формула разности квадратов. Разложение многочленов на множители.
Уравнения. Уравнение, корень уравнения, правила преобразования уравнения, равносильность уравнений. Линейное уравнение с одной переменной, число корней линейного уравнения, решение линейных уравнений. Составление уравнений по условию задачи. Решение текстовых задач спомощью уравнений.
Следующее содержание ПРП изложено в разделе «Системы двух линейных уравнений с двумя неизвестными» рассматриваемого УМК: Линейное уравнение с двумя переменными и его график. Система двух линейных уравнений с двумя переменными. Решение систем уравнений способом подстановки. Примеры решения текстовых задач с помощью систем уравнений.
Координаты и графики. Функции.
Координата точки на прямой. Прямоугольная система координат, оси Ox и Oy. Абсцисса и ордината точки на координатной плоскости. Примеры графиков, заданных формулами. Чтение графиков реальных зависимостей. Понятие функции. График функции. Свойства функций. Линейная функция, её график. График функции y = | х|. Графическое
решение линейных уравнений и систем линейных уравнений.
|
Раздела «Числа и вычисления» в данном УМК нет. Но некоторые темы излагаются в других разделах.
Числовые промежутки. Расстояние между двумя точками координатной прямой.
|
Задание № 2.
Проанализируйте учебные задания (методический аппарат УМК) по выбранной теме, распределите учебные задания по видам формируемых метапредметных результатов.
УМК Мерзляк А.Г. Математика – 6 класс
Тема: Распределительное свойство умножения (параграф 39)
Метапредметные результаты
|
Учебные задания
|
1) Универсальные познавательные действия обеспечивают формирование базовых когнитивных процессов обучающихся (освоение методов познания окружающего мира; применение логических, исследовательских операций, умений работать с информацией).
Базовые логические действия:
выявлять и характеризовать существенные признаки математических объектов, понятий, отношений между понятиями; формулировать определения понятий; устанавливать существенный признак классификации, основания для обобщения и сравнения, критерии проводимого анализа;
выявлять математические закономерности, взаимосвязи и противоречия в фактах, данных, наблюдениях и утверждениях; предлагать критерии для выявления закономерностей и противоречий;
выбирать способ решения учебной задачи (сравнивать несколько вариантов решения, выбирать наиболее подходящий с учётом самостоятельно выделенных критериев).
Базовые исследовательские действия:
использовать вопросы как исследовательский инструмент познания; формулировать вопросы, фиксирующие противоречие, проблему, самостоятельно устанавливать искомое и данное, формировать гипотезу, аргументировать свою позицию, мнение;
самостоятельно формулировать обобщения и выводы по результатам проведённого наблюдения, исследования, оценивать достоверность полученных результатов, выводов и обобщений;
прогнозировать возможное развитие процесса, а также выдвигать предположения о его развитии в новых условиях.
Работа с информацией:
выявлять недостаточность и избыточность информации, данных, необходимых для решения задачи;
выбирать, анализировать, систематизировать и интерпретировать информацию различных видов и форм представления;
выбирать форму представления информации и иллюстрировать решаемые задачи схемами, диаграммами, иной графикой и их комбинациями;
оценивать надёжность информации по критериям, предложенным учителем или сформулированным самостоятельно.
|
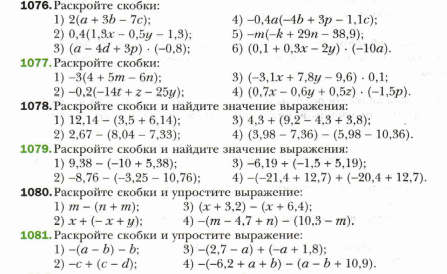


|
2) Универсальные коммуникативные действия обеспечивают сформированность социальных навыков обучающихся.
Общение:
воспринимать и формулировать суждения в соответствии с условиями и целями общения; ясно, точно, грамотно выражать свою точку зрения в устных и письменных текстах, давать пояснения по ходу решения задачи, комментировать полученный результат;
в ходе обсуждения задавать вопросы по существу обсуждаемой темы, проблемы, решаемой задачи, высказывать идеи, нацеленные на поиск решения; сопоставлять свои суждения с суждениями других участников диалога, обнаруживать различие и сходство позиций; в корректной форме формулировать разногласия, свои возражения.
Сотрудничество:
понимать и использовать преимущества командной и индивидуальной работы при решении учебных математических задач; принимать цель совместной деятельности, планировать организацию совместной работы, распределять виды работ, договариваться, обсуждать процесс и результат работы; обобщать мнения нескольких людей;
|

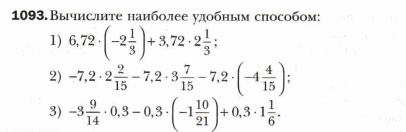
|
3) Универсальные регулятивные действия обеспечивают формирование смысловых установок и жизненных навыков личности. Самоорганизация:
самостоятельно составлять план, алгоритм решения задачи (или его часть), выбирать способ решения с учётом имеющихся ресурсов и собственных возможностей, аргументировать и корректировать варианты решений с учётом новой информации.
Самоконтроль:
владеть способами самопроверки, самоконтроля процесса и результата решения математической задачи;
предвидеть трудности, которые могут возникнуть при решении задачи, вносить коррективы в деятельность на основе новых обстоятельств, найденных ошибок, выявленных трудностей;
оценивать соответствие результата деятельности поставленной цели и условиям, объяснять причины достижения или недостижения цели, находить ошибку, давать оценку приобретённому опыту.
|


| |
 Скачать 2.46 Mb.
Скачать 2.46 Mb.