Контрольная работа (35 вариантов) Теория вероятностей и математическая статистика

• Название: Контрольная работа (35 вариантов) Теория вероятностей и математическая статистика
• Дата: 19.09.2022
• Размер: 289.78 Kb.
• Имя файла: kontrolnaya_4_semestr.docx
• Тип: Контрольная работа; #684356
• страница: 1 из 5

Контрольная работа (35 вариантов) Теория вероятностей и математическая статистика

Y- порядковый номер первой буквы имени студента в алфавите

Z -порядковый номер первой буквы фамилии студента в алфавите

M -порядковый номер первой буквы отчества студента в алфавите

Вариант 1

1. По каналу связи последовательно передаются три сообщения. Каждое из них может быть передано правильно или искаженно. Рассматриваются события: - i-е сообщение передано правильно, - i-е сообщение искажено; i=1,2,3. Выразить в виде сумм, произведений или сумм произведений событий и событие – не более одного сообщения передано правильно.

2. В лотерее 10 билетов, из которых 4 выигрышных. Какова вероятность хотя бы одного выигрыша при покупке четырех билетов.

3. С первого автомата получают на сборку 80 %, а со второго – 20 % одних и тех же деталей. На первом автомате брак составляет 1 %, а на втором – 4 %. Проверенная деталь оказалась бракованной. Определить вероятность того, что эта деталь изготовлена:

1) на первом автомате;

2) на втором автомате.

4. Известно, что 95 % выпускаемой продукции удовлетворяет стандарту. Упрощенная схема контроля признает пригодной продукцию с вероятностью 0,98 и нестандартной с вероятностью 0,06. Определить вероятность того, что изделие, прошедшее контроль, удовлетворяет стандарту.

5. Дана функция плотности: Найти функцию распределения и Дисперсию

6. Производится взвешивание некоторого вещества без систематических погрешностей. Случайные погрешности взвешивания подчинены нормальному закону со средним квадратическим отклонением 20г. Найти вероятность того, что взвешивание будет произведено с погрешностью, не превосходящей по абсолютной величине 10г.

7. Дан статистический ряд: 3, 5, 7, 1, Y, Z, M, 7, 9, 10, 2, 3, 4, M, 7, 8, 9, 6, Y, 10, 12, 1, 2, 6, Z, 8, 15, 3, 2, 6, 8, Y, 16, 1, 6, 19, 4, 6, Y, 5, 20, 11, M, 13, 17, 5, Z, 13, 9, 14, 18, 7, 3, 2, 8, 20, M, 19, 1, 5, 8, 9, 3, 2, 17, Y, Z, M, 1, 19, 4, 7, 8, 3, 20, 1, 14, 9, 5, 15, 17, 3, 13, 2, 8, 6, 7, 4, 11, 1, 3, 7, 5, 8, 10, 18, 12, 17, 3, 5

а) составить ранжированный ряд

б) составить вариационный ряд

в) составить полигон распределения ряда

г) составить гистограмму частот ряда

д) составить эмпирическую функцию распределения

е) найти выборочную среднюю

ж) найти выборочную дисперсию

Вариант 2

1. Машинно-котельная установка состоит из двух котлов и одной машины. Событие А - машина исправна, 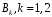– исправен k-й котел. Событие С означает работоспособность машинно-котельной установки (т.е. случай, когда исправны машина и хотя бы один котел). Выразить событие С через А и .

2. В урне 10 шаров, из них 6 – окрашенные. Найти вероятность того, что ровно 2 из 3-х вынутых наудачу шаров окрашены.

3. Радиоаппаратура состоит из 1000 элементов. Вероятность безотказной работы одного элемента в течение одного года работы 0,001 и не зависит от состояния других элементов. Какова вероятность отказа двух элементов за год?

4. По статистическим данным в ремонтной мастерской в среднем на 20 остановок токарного станка приходится: 10 – из-за поломки резца, 3 – из-за неисправности привода, 2 – из-за несвоевременной подачи заготовок. Остальные остановки происходят по другим причинам. Найти вероятность остановки станка по каждой из вышеуказанных причин.

5. Найти математическое ожидание и дисперсию числа лотерейных билетов, на которые выпадут выигрыши, если будет приобретено 40 билетов, причем вероятность выигрыша на каждый равна 0,05.

6. Нормально распределенная случайная величина 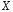задана плотностью распределения . Найти вероятность попадания случайной величины в интервале (-1,1).

7. Дан статистический ряд: 3, 5, 7, 1, Y, Z, M, 7, 9, 10, 2, 3, 4, M, 7, 8, 9, 6, Y, 10, 12, 1, 2, 6, Z, 8, 15, 3, 2, 6, 8, Y, 16, 1, 6, 19, 4, 6, Y, 5, 20, 11, M, 13, 17, 5, Z, 13, 9, 14, 18, 7, 3, 2, 8, 20, M, 19, 1, 5, 8, 9, 3, 2, 17, Y, Z, M, 2, 19, 4, 7, 8, 3, 20, 1, 14, 9, 5, 15, 17, 3, 13, 2, 8, 6, 7, 4, 11, 1, 3, 7, 5, 8, 10, 18, 12, 17, 3, 5

а) составить ранжированный ряд

б) составить вариационный ряд

в) составить полигон распределения ряда

г) составить гистограмму частот ряда

д) составить эмпирическую функцию распределения

е) найти выборочную среднюю

ж) найти выборочную дисперсию

Вариант 3

1. Судно имеет рулевое устройство, 4 котла и 2 турбины. Событие А означает неисправность рулевого устройства, событие 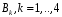– исправность k-го котла, а событие – исправность j-й турбины. Событие Д – судно управляемо (т.е. исправны рулевое устройство, хотя бы один котел и хотя бы одна турбина). Выразите событие Д через события А, .

2. В ящике 15 деталей, из них 6 – бракованные. Найти вероятность того, что ровно одна из трех вынутых деталей – бракованная.

3. Найти вероятность того, что событие А появится не менее трех раз в четырех независимых испытаниях, если вероятность появления события А в одном испытании равна 0,4.

4. Имеются 10 одинаковых урн, в 9-ти из которых находится по 2 черных и 2 белых шара, а в одной – 5 белых и 1 черный шар. Из взятой наудачу урны извлечен белый шар. Какова вероятность того, что этот шар извлечен из урны, содержащей 5 белых шаров.

5. Найти дисперсию дискретной случайной величины 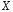- числа появления события А в двух независимых испытаниях, если вероятности появления события в каждом испытании постоянны и одинаковы, а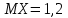

6. Случайная величина – ошибка измерения, распределена по

нормальному закону. Найти , где , если систематические погрешности отсутствуют.

7. Дан статистический ряд: 3, 5, 7, 1, Y, Z, M, 7, 9, 10, 2, 3, 4, M, 7, 8, 9, 6, Y, 10, 12, 1, 2, 6, Z, 8, 15, 3, 2, 6, 8, Y, 16, 1, 6, 19, 4, 6, Y, 5, 20, 11, M, 13, 17, 5, Z, 13, 9, 14, 18, 7, 3, 2, 8, 20, M, 19, 1, 5, 8, 9, 3, 2, 17, Y, Z, M, 3, 19, 4, 7, 8, 3, 20, 1, 14, 9, 5, 15, 17, 3, 13, 2, 8, 6, 7, 4, 11, 1, 3, 7, 5, 8, 10, 18, 12, 17, 3, 5

а) составить ранжированный ряд

б) составить вариационный ряд

в) составить полигон распределения ряда

г) составить гистограмму частот ряда

д) составить эмпирическую функцию распределения

е) найти выборочную среднюю

ж) найти выборочную дисперсию

Вариант 4

1. Прибор состоит из 2-х блоков первого типа и 3-х блоков второго типа. Событие 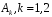означает исправность k-го блока первого типа, а событие – исправность i-го блока второго типа. Прибор исправен, если исправны хотя бы один блок первого типа и не менее двух блоков второго типа. Выразить событие С – исправность прибора – через события и .

2. Шар радиуса R брошен в проволочную сетку с квадратными сетками со стороной 6R. Найти вероятность того, что шар пролетит сквозь сетку, не задев ее.

3. Число грузовых автомашин, проезжающих по шоссе, на котором стоит бензоколонка, относится к числу легковых машин как 3:7. Вероятность того, что на данной бензоколонке будет заправляться грузовая автомашина равна 0,1, а легковая – 0,2. Найти вероятность того, что для заправки к бензоколонке подъедет грузовая машина.

4. Имеется 2 набора деталей. Вероятность того, что деталь из 1-го набора стандартна, равна 0,8, а из 2-го – 0,9. Найти вероятность того, что взятая наугад деталь (из наудачу взятого набора) стандартна.

5. По железнодорожному мосту, независимо один от другого, производят серийное бомбометание три самолета. Каждый сбрасывает 1 серию бомб. Вероятность попадания хотя бы одной бомбы из серии для первого самолета равна 0,2, для второго – 0,4, для третьего – 0,5. Найти вероятность разрушения моста.

6. Случайная величина имеет нормальное распределение с и . Что больше: или ?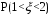

7. Дан статистический ряд: 3, 5, 7, 1, Y, Z, M, 7, 9, 10, 2, 3, 4, M, 7, 8, 9, 6, Y, 10, 12, 1, 2, 6, Z, 8, 15, 3, 2, 6, 8, Y, 16, 1, 6, 19, 4, 6, Y, 5, 20, 11, M, 13, 17, 5, Z, 13, 9, 14, 18, 7, 3, 2, 8, 20, M, 19, 1, 5, 8, 9, 3, 2, 17, Y, Z, M, 4, 19, 4, 7, 8, 3, 20, 1, 14, 9, 5, 15, 17, 3, 13, 2, 8, 6, 7, 4, 11, 1, 3, 7, 5, 8, 10, 18, 12, 17, 3, 5

а) составить ранжированный ряд

б) составить вариационный ряд

в) составить полигон распределения ряда

г) составить гистограмму частот ряда

д) составить эмпирическую функцию распределения

е) найти выборочную среднюю

ж) найти выборочную дисперсию

Вариант 5

1. События А,В,С означают, что взято хотя бы по одной книге из трех различных собраний сочинений, каждое из которых содержит, по крайней мере, 3 тома. События 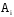и означают, что из первого собрания взято i, а из второго k томов соответственно. Что означают события: ?

2. Из 28 костей домино случайно выбираются две. Найти вероятность того, что из них можно составить "цепочку" согласно правилам игры.

3. Линия связи с 1 каналом обслуживания соединяет пункт А с 10 абонентами пункта В. Все абоненты одинаково часто и независимо друг от друга пользуются телефоном со средней продолжительностью телефонного разговора 6 минут в час. Найти вероятность того, что линия будет занята.

4. В трех урнах имеются белые и черные шары. В первой урне 3 белых и 1 черный шар, во второй – 6 белых и 4 черных, в третьей – 9 белых и 1 черный. Из наугад выбранной урны случайным образом вынимается шар. Найти вероятность того, что он окажется белым.

5. Дана функция плотности: Найти значение и математическое ожидание .

6. Вероятность попадания в цель при одном выстреле равна 0,01. Найти приближенное значение вероятности того, что при 100 выстрелах будет не более трех попаданий.

7. Дан статистический ряд: 3, 5, 7, 1, Y, Z, M, 7, 9, 10, 2, 3, 4, M, 7, 8, 9, 6, Y, 10, 12, 1, 2, 6, Z, 8, 15, 3, 2, 6, 8, Y, 16, 1, 6, 19, 4, 6, Y, 5, 20, 11, M, 13, 17, 5, Z, 13, 9, 14, 18, 7, 3, 2, 8, 20, M, 19, 1, 5, 8, 9, 3, 2, 17, Y, Z, M, 5, 19, 4, 7, 8, 3, 20, 1, 14, 9, 5, 15, 17, 3, 13, 2, 8, 6, 7, 4, 11, 1, 3, 7, 5, 8, 10, 18, 12, 17, 3, 5

а) составить ранжированный ряд

б) составить вариационный ряд

в) составить полигон распределения ряда

г) составить гистограмму частот ряда

д) составить эмпирическую функцию распределения

е) найти выборочную среднюю

ж) найти выборочную дисперсию

Вариант 6

1. Из урны, содержащей черные и белые шары, извлечены n шаров. Пусть – событие, состоящее в том, что i-й шар белый, i=1,..,n. Выразить через следующие события:

1) все шары белые;

2) хотя бы один шар белый;

3) ровно один шар белый.

2. Студент знает 25 из 30 вопросов экзамена. Найти вероятность того, что студент сдаст экзамен, если для этого достаточно ответить на 3 из 5 предложенных экзаменатором вопроса.

3. Автомат штампует детали. Вероятность того, что за один час не будет выпущено ни одной стандартной детали, равна 0,9. Найти вероятность того, что будут стандартными все детали, выпущенные за три часа.

4. Коммутатор учреждения обслуживает 100 абонентов. Вероятность того, что в течение 1 минуты поступит звонок на коммутатор, равна 0,01. Найти вероятность того, что в течение 1 минуты позвонят менее 3-х абонентов.

5. Найти дисперсию дискретной случайной величины, заданной законом распределения:

X	10	13	17	25	10
P	0,1	0,1	0,3	0,2	0,3

6. Чему равна вероятность того, что нормальная случайная величина 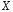c и примет значение из интервала ?

7. Дан статистический ряд: 3, 5, 7, 1, Y, Z, M, 7, 9, 10, 2, 3, 4, M, 7, 8, 9, 6, Y, 10, 12, 1, 2, 6, Z, 8, 15, 3, 2, 6, 8, Y, 16, 1, 6, 19, 4, 6, Y, 5, 20, 11, M, 13, 17, 5, Z, 13, 9, 14, 18, 7, 3, 2, 8, 20, M, 19, 1, 5, 8, 9, 3, 2, 17, Y, Z, M, 6, 19, 4, 7, 8, 3, 20, 1, 14, 9, 5, 15, 17, 3, 13, 2, 8, 6, 7, 4, 11, 1, 3, 7, 5, 8, 10, 18, 12, 17, 3, 5

а) составить ранжированный ряд

б) составить вариационный ряд

в) составить полигон распределения ряда

г) составить гистограмму частот ряда

д) составить эмпирическую функцию распределения

е) найти выборочную среднюю

ж) найти выборочную дисперсию

Вариант 7

1. Из урны, содержащей черные и белые шары, извлечены m шаров. Пусть – событие, состоящее в том, что k-й шар белый, k=1,..,m. Выразить через следующие события:

1) не более i шаров белые 1;

2) по крайней мере i шаров белые;

3) ровно i шаров белые.

2. В колоде 20 перфокарт, из них 1 помятая. Найти вероятность того, что среди 5 взятых наудачу из колоды перфокарт не будет ни одной помятой.

3. В электрическую цепь последовательно включены три элемента, работающие независимо друг от друга. Вероятности отказов первого, второго и третьего элементов соответственно равны 0,1; 0,15; 0,2. Найти вероятность того, что тока в цепи не будет.

4. В цехе три типа автоматов производят одни и те же детали. Производительность их одинакова, но качество работы различно. Известно, что станки первого типа производят 0,9 деталей отличного качества, второго типа – 0,85 и третьего – 0,8. Все произведенные в цехе за смену детали в не рассортированном виде сложены на складе. Определить вероятность того, что взятая наудачу деталь окажется отличного качества, если станков первого типа – 20, второго – 8, третьего – 2.

5. Найти дисперсию дискретной случайной величины, заданной законом распределения:

X	1	2,5	3	3,5	4
P	0,1	0,2	0,3	0,1	0,3

6. Ребро куба измерено приближенно, причем . Рассматривая ребро куба как случайную величину