Контрольная работа (35 вариантов) Теория вероятностей и математическая статистика
 Скачать 289.78 Kb.
|
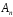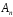K контролерами; если n-й контролер обнаружил дефект, то это событие обозначают  . Изделие бракуется, если будет найден хотя бы один дефект. Используя алгебру событий, выразить через следующие события:A – изделие будет забраковано; B – изделие будет забраковано вторым контролером; C – изделие будет забраковано всеми контролерами. 2. Из 12 билетов, пронумерованных от 1 до 12, один за другим выбираются наугад 2 билета. Какова вероятность того, что на этих билетах оба номера четные? 3. Вероятность безотказной работы блока, входящего в систему, в течение заданного времени составляет 0,8. Для повышения надежности устанавливают такой же резервный блок. Требуется найти вероятность безотказной работы системы с учетом резервного блока. 4. Трое охотников выстрелят по медведю. Вероятность попадания в цель для первого охотника равна 0,7, для второго – 0,8, а для третьего – 0,5. Если медведь будет убит одной пулей, то какова вероятность, что он убит первым охотником? 5. Вычислить математическое ожидание случайной величины X, обладающей плотностью распределения: 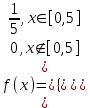 6. Найти математическое ожидание и дисперсию случайной величины X, равномерно распределенной в интервале (12,18). 7. Дан статистический ряд: 3, 5, 7, 1, Y, Z, M, 7, 9, 10, 2, 3, 4, M, 7, 8, 9, 6, Y, 10, 12, 1, 2, 6, Z, 8, 15, 3, 2, 6, 8, Y, 16, 1, 6, 19, 4, 6, Y, 5, 20, 11, M, 13, 17, 5, Z, 13, 9, 14, 18, 7, 3, 2, 8, 20, M, 19, 1, 5, 8, 9, 3, 2, 17, Y, Z, M, 2, 19, 4, 7, 8, 3, 20, 1, 14, 9, 5, 15, 17, 3, 13, 2, 8, 6, 7, 4, 11, 1, 3, 7, 5, 8, 10, 18, 12, 17, 3, 5 а) составить ранжированный ряд б) составить вариационный ряд в) составить полигон распределения ряда г) составить гистограмму частот ряда д) составить эмпирическую функцию распределения е) найти выборочную среднюю ж) найти выборочную дисперсию Вариант 23 1. В урне 5 красных, 2 синих и 3 белых шара. Все пронумерованы цифрами 1,2,...,10. Из урны наудачу будет взят один шар. События: A – шар с четным номером; B – шар с номером, кратным 3; C – шар красного цвета; D – шар синего цвета; E – шар белого цвета. Что представляют собой события A+B, C+E, AD, 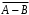 ,  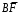,  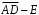?2. В партии, состоящей из 20 изделий, имеется 3 дефектных. Из партии выбирается наудачу для контроля 5 изделий. Найти вероятность того, что из них 2 изделия дефектных. 3. Электрическая цепь состоит из двух последовательно соединенных элементов 1 и 2. Элементы цепи выходят из строя независимо друг от друга с вероятностям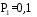и  и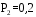 . Определить вероятность прерывания испытания.4. Сборщик получил 3 коробки деталей, изготовленных первым цехом, и 2 коробки деталей, изготовленных вторым цехом. Вероятность того, что деталь первого цеха стандартна, равна 0,8, а второго цеха - 0,9. Сборщик извлек деталь из наудачу взятой коробки. Найти вероятность того, что извлеченная деталь стандартна. 5. Случайная величина X задана функцией распределения 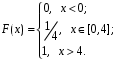 Найти математическое ожидание случайной величины X. 6. Случайная величина X распределена нормально с математическим ожиданием a=10. Вероятность попадания X в интервал (0,10) равна 0,3. Чему равна вероятность попадания в интервал (10,20)? 7. Дан статистический ряд: 3, 5, 7, 1, Y, Z, M, 7, 9, 10, 2, 3, 4, M, 7, 8, 9, 6, Y, 10, 12, 1, 2, 6, Z, 8, 15, 3, 2, 6, 8, Y, 16, 1, 6, 19, 4, 6, Y, 5, 20, 11, M, 13, 17, 5, Z, 13, 9, 14, 18, 7, 3, 2, 8, 20, M, 19, 1, 5, 8, 9, 3, 2, 17, Y, Z, M, 3, 19, 4, 7, 8, 3, 20, 1, 14, 9, 5, 15, 17, 3, 13, 2, 8, 6, 7, 4, 11, 1, 3, 7, 5, 8, 10, 18, 12, 17, 3, 5 а) составить ранжированный ряд б) составить вариационный ряд в) составить полигон распределения ряда г) составить гистограмму частот ряда д) составить эмпирическую функцию распределения е) найти выборочную среднюю ж) найти выборочную дисперсию Вариант 24 1. В поле наблюдения микроскопа попадут четыре клетки. За время наблюдения каждая из них может как разделиться, так и не разделиться. Рассматриваются события: A – разделится одна клетка; B – разделится хотя бы одна клетка; C – разделятся не менее двух клеток; D – разделятся две клетки; E – разделятся три клетки; F – разделятся все четыре клетки. В чем состоят события: A+B, AB, B+C, D+E+F, BC, BF? Верны ли равенства: BF=CF, BC=D? 2. На отрезке AB длины l поставлены наудачу три точки. Найти вероятность того, что одна точка будет находиться от точки A на расстоянии меньшем X, а две точки на расстоянии, большем X, если вероятность попадания точки на какую-нибудь часть отрезка зависит только от длины этой части и пропорциональна ей. 3. В тире имеется пять ружей, вероятности попадания из которых соответственно равны: 0,5; 0,6; 0,7; 0,8; 0,9. Определить вероятность попадания при одном выстреле из произвольно взятого ружья. 4. Статистика показывает, что среди двоен оказывается 28 % идентичных и 72 % неидентичных близнецов. Среди идентичных близнецов 100 % двоен одного пола. Среди неидентичных близнецов 50 % двоен разного пола. Найти вероятность того, что наугад выбранные близнецы одного пола. 5. Студент помнит, что плотность распределения имеет вид: 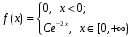 однако он забыл, чему равна постоянная C. Требуется найти C. 6. Деталь, изготовленная автоматом, считается годной, если отклонение ее контролируемого размера от стандарта не превышает 10 мм. Случайные отклонения контролируемого размера от стандарта подчинены нормальному закону со средним a=1 и средним квадратическим отклонением 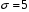 . Найти вероятность того, что из трех деталей не менее двух деталей окажутся годными.7. Дан статистический ряд: 3, 5, 7, 1, Y, Z, M, 7, 9, 10, 2, 3, 4, M, 7, 8, 9, 6, Y, 10, 12, 1, 2, 6, Z, 8, 15, 3, 2, 6, 8, Y, 16, 1, 6, 19, 4, 6, Y, 5, 20, 11, M, 13, 17, 5, Z, 13, 9, 14, 18, 7, 3, 2, 8, 20, M, 19, 1, 5, 8, 9, 3, 2, 17, Y, Z, M, 4, 19, 4, 7, 8, 3, 20, 1, 14, 9, 5, 15, 17, 3, 13, 2, 8, 6, 7, 4, 11, 1, 3, 7, 5, 8, 10, 18, 12, 17, 3, 5 а) составить ранжированный ряд б) составить вариационный ряд в) составить полигон распределения ряда г) составить гистограмму частот ряда д) составить эмпирическую функцию распределения е) найти выборочную среднюю ж) найти выборочную дисперсию Вариант 25 1. Прибор состоит из двух блоков. Первый блок состоит из четырех одинаковых деталей и работает при исправности хотя бы трех из них. Второй блок состоит из пяти одинаковых деталей и работает при исправности хотя бы двух из них. Обозначим:  – исправна k-я деталь первого блока, k=1,2,3,4, и 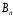 – исправна n-я деталь второго блока, n=1,2,3,4,5. Выразить через , 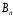и противоположные им следующие события:A – работает первый блок; B – не работает первый блок; C – работает второй блок; D – не работает второй блок; E – прибор работает; F – прибор не работает. 2. У сборщика 16 деталей, изготовленных первым заводом, и 4 детали, изготовленные вторым заводом. Наудачу извлекаются две детали. Найти вероятность того, что хотя бы одна деталь окажется изготовленной на первом заводе. 3. При увеличении напряжения в два раза может произойти разрыв электрической цепи вследствие выхода из строя одного из трех последовательно соединенных элементов с вероятностями соответственно 0,3; 0,4; 0,5. Определить вероятность того, что не будет разрыва цепи. 4. При приемке партии подвергается проверке половина изделий. Условие приемки - наличие брака в выборке не более 2 %. Найти вероятность того, что партия из 100 изделий, содержащая 5 % брака, не будет принята. 5. Случайная величина X задана функцией распределения 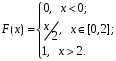 Найти плотность распределения и математическое ожидание случайной величины X. 6. Случайные ошибки измерения подчинены нормальному закону со средним a=0 и 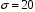 . Найти вероятность того, что из четырех независимых измерений только одна из них не превзойдет по абсолютной величине 10 мм. 7. Дан статистический ряд: 3, 5, 7, 1, Y, Z, M, 7, 9, 10, 2, 3, 4, M, 7, 8, 9, 6, Y, 10, 12, 1, 2, 6, Z, 8, 15, 3, 2, 6, 8, Y, 16, 1, 6, 19, 4, 6, Y, 5, 20, 11, M, 13, 17, 5, Z, 13, 9, 14, 18, 7, 3, 2, 8, 20, M, 19, 1, 5, 8, 9, 3, 2, 17, Y, Z, M, 5, 19, 4, 7, 8, 3, 20, 1, 14, 9, 5, 15, 17, 3, 13, 2, 8, 6, 7, 4, 11, 1, 3, 7, 5, 8, 10, 18, 12, 17, 3, 5 а) составить ранжированный ряд б) составить вариационный ряд в) составить полигон распределения ряда г) составить гистограмму частот ряда д) составить эмпирическую функцию распределения е) найти выборочную среднюю ж) найти выборочную дисперсию Вариант 26 1. Прибор состоит из 2-х блоков первого типа и 3-х блоков второго типа. Событи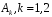е  означает исправность k-го блока первого типа, а событие  – исправность i-го блока второго типа. Прибор исправен, если исправны хотя бы один блок первого типа и не менее двух блоков второго типа. Выразить событие С – исправность прибора – через события и  .2. Шар радиуса R брошен в проволочную сетку с квадратными сетками со стороной 6R. Найти вероятность того, что шар пролетит сквозь сетку, не задев ее. 3. Число грузовых автомашин, проезжающих по шоссе, на котором стоит бензоколонка, относится к числу легковых машин как 3:7. Вероятность того, что на данной бензоколонке будет заправляться грузовая автомашина равна 0,1, а легковая – 0,2. Найти вероятность того, что для заправки к бензоколонке подъедет грузовая машина. 4. Имеется 2 набора деталей. Вероятность того, что деталь из 1-го набора стандартна, равна 0,8, а из 2-го – 0,9. Найти вероятность того, что взятая наугад деталь (из наудачу взятого набора) стандартна. 5. По железнодорожному мосту, независимо один от другого, производят серийное бомбометание три самолета. Каждый сбрасывает 1 серию бомб. Вероятность попадания хотя бы одной бомбы из серии для первого самолета равна 0,2, для второго – 0,4, для третьего – 0,5. Найти вероятность разрушения моста. 6. Случайная величина  имеет нормальное распределение с  и  . Что больше:  или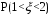 ?7. Дан статистический ряд: 3, 5, 7, 1, Y, Z, M, 7, 9, 10, 2, 3, 4, M, 7, 8, 9, 6, Y, 10, 12, 1, 2, 6, Z, 8, 15, 3, 2, 6, 8, Y, 16, 1, 6, 19, 4, 6, Y, 5, 20, 11, M, 13, 17, 5, Z, 13, 9, 14, 18, 7, 3, 2, 8, 20, M, 19, 1, 5, 8, 9, 3, 2, 17, Y, Z, M, 6, 19, 4, 7, 8, 3, 20, 1, 14, 9, 5, 15, 17, 3, 13, 2, 8, 6, 7, 4, 11, 1, 3, 7, 5, 8, 10, 18, 12, 17, 3, 5 а) составить ранжированный ряд б) составить вариационный ряд в) составить полигон распределения ряда г) составить гистограмму частот ряда д) составить эмпирическую функцию распределения е) найти выборочную среднюю ж) найти выборочную дисперсию Вариант 27 1. События А,В,С означают, что взято хотя бы по одной книге из трех различных собраний сочинений, каждое из которых содержит, по крайней мере, 3 тома. События 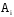 и  означают, что из первого собрания взято i, а из второго k томов соответственно. Что означают события:  ?2. Из 28 костей домино случайно выбираются две. Найти вероятность того, что из них можно составить "цепочку" согласно правилам игры. 3. Линия связи с 1 каналом обслуживания соединяет пункт А с 10 абонентами пункта В. Все абоненты одинаково часто и независимо друг от друга пользуются телефоном со средней продолжительностью телефонного разговора 6 минут в час. Найти вероятность того, что линия будет занята. 4. В трех урнах имеются белые и черные шары. В первой урне 3 белых и 1 черный шар, во второй – 6 белых и 4 черных, в третьей – 9 белых и 1 черный. Из наугад выбранной урны случайным образом вынимается шар. Найти вероятность того, что он окажется белым. 5. Дана функция плотности:  Найти значение  и  .6. Вероятность попадания в цель при одном выстреле равна 0,01. Найти приближенное значение вероятности того, что при 100 выстрелах будет не более трех попаданий. 7. Дан статистический ряд: 3, 5, 7, 1, Y, Z, M, 7, 9, 10, 2, 3, 4, M, 7, 8, 9, 6, Y, 10, 12, 1, 2, 6, Z, 8, 15, 3, 2, 6, 8, Y, 16, 1, 6, 19, 4, 6, Y, 5, 20, 11, M, 13, 17, 5, Z, 13, 9, 14, 18, 7, 3, 2, 8, 20, M, 19, 1, 5, 8, 9, 3, 2, 17, Y, Z, M, 7, 19, 4, 7, 8, 3, 20, 1, 14, 9, 5, 15, 17, 3, 13, 2, 8, 6, 7, 4, 11, 1, 3, 7, 5, 8, 10, 18, 12, 17, 3, 5 а) составить ранжированный ряд б) составить вариационный ряд в) составить полигон распределения ряда г) составить гистограмму частот ряда д) составить эмпирическую функцию распределения е) найти выборочную среднюю ж) найти выборочную дисперсию Вариант 28 1. Из урны, содержащей черные и белые шары, извлечены n шаров. Пусть  – событие, состоящее в том, что i-й шар белый, i=1,..,n. Выразить через следующие события:1) все шары белые; 2) хотя бы один шар белый; 3) ровно один шар белый. 2. Студент знает 25 из 30 вопросов экзамена. Найти вероятность того, что студент сдаст экзамен, если для этого достаточно ответить на 3 из 5 предложенных экзаменатором вопроса. 3. Автомат штампует детали. Вероятность того, что за один час не будет выпущено ни одной стандартной детали, равна 0,9. Найти вероятность того, что будут стандартными все детали, выпущенные за три часа. 4. Коммутатор учреждения обслуживает 100 абонентов. Вероятность того, что в течение 1 минуты поступит звонок на коммутатор, равна 0,01. Найти вероятность того, что в течение 1 минуты позвонят менее 3-х абонентов. 5. Найти дисперсию дискретной случайной величины, заданной законом распределения:
6. Чему равна вероятность того, что нормальная случайная величина 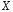 c  и  примет значение из интервала  ?7. Дан статистический ряд: 3, 5, 7, 1, Y, Z, M, 7, 9, 10, 2, 3, 4, M, 7, 8, 9, 6, Y, 10, 12, 1, 2, 6, Z, 8, 15, 3, 2, 6, 8, Y, 16, 1, 6, 19, 4, 6, Y, 5, 20, 11, M, 13, 17, 5, Z, 13, 9, 14, 18, 7, 3, 2, 8, 20, M, 19, 1, 5, 8, 9, 3, 2, 17, Y, Z, M, 8, 19, 4, 7, 8, 3, 20, 1, 14, 9, 5, 15, 17, 3, 13, 2, 8, 6, 7, 4, 11, 1, 3, 7, 5, 8, 10, 18, 12, 17, 3, 5 а) составить ранжированный ряд б) составить вариационный ряд в) составить полигон распределения ряда г) составить гистограмму частот ряда д) составить эмпирическую функцию распределения е) найти выборочную среднюю ж) найти выборочную дисперсию Вариант 29 1. Из урны, содержащей черные и белые шары, извлечены |