Контрольная работа (35 вариантов) Теория вероятностей и математическая статистика
 Скачать 289.78 Kb. Скачать 289.78 Kb.
|
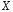 , распределенную равномерно в интервале (a,b), найти математическое ожидание и дисперсию объема куба. , распределенную равномерно в интервале (a,b), найти математическое ожидание и дисперсию объема куба.7. Дан статистический ряд: 3, 5, 7, 1, Y, Z, M, 7, 9, 10, 2, 3, 4, M, 7, 8, 9, 6, Y, 10, 12, 1, 2, 6, Z, 8, 15, 3, 2, 6, 8, Y, 16, 1, 6, 19, 4, 6, Y, 5, 20, 11, M, 13, 17, 5, Z, 13, 9, 14, 18, 7, 3, 2, 8, 20, M, 19, 1, 5, 8, 9, 3, 2, 17, Y, Z, M, 7, 19, 4, 7, 8, 3, 20, 1, 14, 9, 5, 15, 17, 3, 13, 2, 8, 6, 7, 4, 11, 1, 3, 7, 5, 8, 10, 18, 12, 17, 3, 5 а) составить ранжированный ряд б) составить вариационный ряд в) составить полигон распределения ряда г) составить гистограмму частот ряда д) составить эмпирическую функцию распределения е) найти выборочную среднюю ж) найти выборочную дисперсию Вариант 8 1. В урне n белых и m черных шаров. Двое будут играть так: будут поочередно доставать шар, не возвращая их в урну. Выигрывает тот, у кого появится белый шар. Используя алгебру событий, выразить события A и B через  и и  , где событие A означает, что выигрывает первый игрок, B – выигрывает второй, , где событие A означает, что выигрывает первый игрок, B – выигрывает второй,  – при i-м извлечении появится белый шар у первого игрока, – при i-м извлечении появится белый шар у первого игрока,  – при i-м извлечении появится белый шар у второго игрока. – при i-м извлечении появится белый шар у второго игрока.2. В группе 20 студентов, из них 6 отличников. Найти вероятность того, что среди трех наудачу отобранных студентов только один отличник. 3. В барабане револьвера семь гнезд, из них в пять заложены патроны, а два оставлены пустыми. Барабан приводится во вращение, в результате чего против ствола случайным образом оказывается одно из гнезд. После этого нажимается спусковой крючок. Если ячейка была пустая, выстрела не происходит. Найти вероятность того, что повторив такой опыт два раза подряд, мы оба раза не выстрелим. 4. Линия связи соединяет пункт A с десятью абонентами пункта B. Все абоненты одинаково часто и независимо друг от друга пользуются телефоном со средней продолжительностью телефонного разговора 6 минут в час. Найти вероятность того, что один из абонентов не сможет дозвониться до нужного ему абонента (т.е. линия будет занята). 5. Случайная величина X обладает плотностью распределения 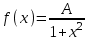 . Найти неизвестное A. . Найти неизвестное A.6. Найти вероятность того, что нормальная случайная величина X с 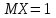 и и 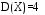 примет значение из интервала (0,5). примет значение из интервала (0,5).7. Дан статистический ряд: 3, 5, 7, 1, Y, Z, M, 7, 9, 10, 2, 3, 4, M, 7, 8, 9, 6, Y, 10, 12, 1, 2, 6, Z, 8, 15, 3, 2, 6, 8, Y, 16, 1, 6, 19, 4, 6, Y, 5, 20, 11, M, 13, 17, 5, Z, 13, 9, 14, 18, 7, 3, 2, 8, 20, M, 19, 1, 5, 8, 9, 3, 2, 17, Y, Z, M, 8, 19, 4, 7, 8, 3, 20, 1, 14, 9, 5, 15, 17, 3, 13, 2, 8, 6, 7, 4, 11, 1, 3, 7, 5, 8, 10, 18, 12, 17, 3, 5 а) составить ранжированный ряд б) составить вариационный ряд в) составить полигон распределения ряда г) составить гистограмму частот ряда д) составить эмпирическую функцию распределения е) найти выборочную среднюю ж) найти выборочную дисперсию Вариант 9 1. Трое игроков A, B, C будут поочередно кидать монету. Выиграет тот, у кого появится герб. Обозначим: событие  – у первого игрока при i -м бросании появится герб; – у первого игрока при i -м бросании появится герб;  – у второго игрока при i-м бросании появится герб; – у второго игрока при i-м бросании появится герб; 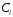 – у третьего игрока при i-м бросании появится герб. Используя алгебру событий, выразить события: A– выигрывает первый игрок; B – выигрывает второй; C – выигрывает третий – через события – у третьего игрока при i-м бросании появится герб. Используя алгебру событий, выразить события: A– выигрывает первый игрок; B – выигрывает второй; C – выигрывает третий – через события  , , , , 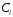 . .2. Из пяти букв разрезной азбуки составлено слово "книга". Ребенок, не умеющий читать, рассыпал эти буквы и затем собрал в произвольном порядке. Найти вероятность того, что у него снова получилось слово "книга". 3. Безотказная работа прибора определяется безотказной работой каждого из трех узлов, составляющих прибор. Вероятность безотказной работы за некоторый цикл соответственно равна 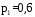 , , 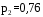 , , 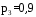 . Найти вероятность безотказной работы прибора за указанный цикл. . Найти вероятность безотказной работы прибора за указанный цикл.4. Имеется 10 одинаковых урн, из которых в 9 находится по 2 черных и 2 белых шара, а в одном - 5 белых и 1 черный шар. Из взятой наудачу урны извлечен белый шар. Какова вероятность того, что этот шар извлечен из урны, содержащей 5 белых шаров. 5. Дана функция плотности:  Найти функцию распределения  и математическое ожидание и математическое ожидание  . .6. Коробки с шоколадом упаковываются автоматически, их средняя масса равна 1,06 кг. Найти стандартное отклонение, если 5 % коробок имеют массу 1 кг. Предполагается, что масса коробок распределена по нормальному закону. 7. Дан статистический ряд: 3, 5, 7, 1, Y, Z, M, 7, 9, 10, 2, 3, 4, M, 7, 8, 9, 6, Y, 10, 12, 1, 2, 6, Z, 8, 15, 3, 2, 6, 8, Y, 16, 1, 6, 19, 4, 6, Y, 5, 20, 11, M, 13, 17, 5, Z, 13, 9, 14, 18, 7, 3, 2, 8, 20, M, 19, 1, 5, 8, 9, 3, 2, 17, Y, Z, M, 9, 19, 4, 7, 8, 3, 20, 1, 14, 9, 5, 15, 17, 3, 13, 2, 8, 6, 7, 4, 11, 1, 3, 7, 5, 8, 10, 18, 12, 17, 3, 5 а) составить ранжированный ряд б) составить вариационный ряд в) составить полигон распределения ряда г) составить гистограмму частот ряда д) составить эмпирическую функцию распределения е) найти выборочную среднюю ж) найти выборочную дисперсию Вариант 10 1. Двое игроков A и B будут поочередно кидать монету. Выиграет тот, у кого появится герб. Обозначим: событие  – у первого игрока при i-м бросании появится герб; – у первого игрока при i-м бросании появится герб;  – у второго игрока при i-м бросании появится герб; A – выигрывает первый игрок; B – выигрывает второй. Используя алгебру событий, выразить события A и B через – у второго игрока при i-м бросании появится герб; A – выигрывает первый игрок; B – выигрывает второй. Используя алгебру событий, выразить события A и B через  и и  . Как меняется i? . Как меняется i?2. В цехе работают 7 мужчин и 3 женщины. По табельным номерам будут отобраны случайным образом три человека. Найти вероятность того, что все отобранные лица – мужчины. 3. Для разрушения моста достаточно одной авиабомбы. Найти вероятность разрушения моста, если на него будут сброшены 4 бомбы с вероятностями попадания соответственно: 0,3; 0,4; 0,5; 0,8. 4. В кошельке лежат три монеты достоинством в 20 копеек и семь монет достоинством в 3 копейки. Наудачу берется одна монета, а затем извлекается вторая монета, оказавшаяся достоинством в 20 копеек. Найти вероятность того, что и первая извлеченная монета имеет достоинство в 20 копеек. 5. Найти дисперсию дискретной случайной величины, заданной законом распределения:
6. Ошибка радиодальномера подчинена нормальному закону. Систематической ошибки радиодальномер не дает. Какова должна быть средняя ошибка (вероятное отклонение), чтобы с вероятностью не меньше 0,95 можно было бы ожидать, что измеренное значение дальности будет отклоняться от истинного не более, чем на 20 м? 7. Дан статистический ряд: 3, 5, 7, 1, Y, Z, M, 7, 9, 10, 2, 3, 4, M, 7, 8, 9, 6, Y, 10, 12, 1, 2, 6, Z, 8, 15, 3, 2, 6, 8, Y, 16, 1, 6, 19, 4, 6, Y, 5, 20, 11, M, 13, 17, 5, Z, 13, 9, 14, 18, 7, 3, 2, 8, 20, M, 19, 1, 5, 8, 9, 3, 2, 17, Y, Z, M, 1, 19, 4, 7, 8, 3, 20, 1, 14, 9, 5, 15, 17, 3, 13, 2, 8, 6, 7, 4, 11, 1, 3, 7, 5, 8, 10, 18, 12, 17, 3, 5 а) составить ранжированный ряд б) составить вариационный ряд в) составить полигон распределения ряда г) составить гистограмму частот ряда д) составить эмпирическую функцию распределения е) найти выборочную среднюю ж) найти выборочную дисперсию Вариант 11 1. В корзину будут сброшены 3 мяча. События  , i=1,2,3 состоят в том, что i-й мяч попадет в корзину. Выразите через , i=1,2,3 состоят в том, что i-й мяч попадет в корзину. Выразите через  события: события:1) B – в корзину попадет один мяч; 2) C – в корзину попадет по крайней мере один мяч; 3) D – в корзину попадут три мяча; 4) H – в корзину не попадет ни одного мяча. 2. В записанном телефонном номере 135-3-... три последние цифры стерлись. В предположении, что все комбинации трех стершихся цифр равновероятны, найти вероятности событий: A={стерлись различные цифры, отличные от 1,2,3} B={стерлись одинаковые цифры} C={две из стершихся цифр совпадают}. 3. Имеется 4 прибора. Вероятность того, что прибор работает в произвольный момент t, равна 0,9. Найти вероятность того, что в момент t работает хотя бы один прибор. 4. На трех дочерей – Анну, Ольгу и Татьяну – в семье возложена обязанность мыть тарелки. Поскольку Анна – старшая, ей приходится выполнять 40 % всей работы, остальные 60 % Ольга и Татьяна делят поровну. Когда Анна моет посуду, вероятность для нее разбить одну тарелку равна 0,02; для Ольги – 0,03 и для Татьяны – 0,02. Родители не знают, кто мыл тарелки вечером, но они слышали звон разбитой тарелки. Какова вероятность того, что посуду мыла Анна? 5. В партии из 10 деталей содержится три нестандартных. Наудачу отобраны две детали. Найти математическое ожидание дискретной случайной величины X – числа нестандартных деталей среди двух отобранных. 6. Пусть известно, что на выпечку 1000 сладких булочек с изюмом полагается 10000 изюмин. Найти вероятность того, что нам достанется булочка вовсе без изюма. 7. Дан статистический ряд: 3, 5, 7, 1, Y, Z, M, 7, 9, 10, 2, 3, 4, M, 7, 8, 9, 6, Y, 10, 12, 1, 2, 6, Z, 8, 15, 3, 2, 6, 8, Y, 16, 1, 6, 19, 4, 6, Y, 5, 20, 11, M, 13, 17, 5, Z, 13, 9, 14, 18, 7, 3, 2, 8, 20, M, 19, 1, 5, 8, 9, 3, 2, 17, Y, Z, M, 1, 19, 4, 7, 8, 3, 20, 1, 14, 9, 5, 15, 17, 3, 13, 2, 8, 6, 7, 4, 11, 1, 3, 7, 5, 8, 10, 18, 12, 17, 3, 5 а) составить ранжированный ряд б) составить вариационный ряд в) составить полигон распределения ряда г) составить гистограмму частот ряда д) составить эмпирическую функцию распределения е) найти выборочную среднюю ж) найти выборочную дисперсию Вариант 12 1. В баскетбольную корзину будет трижды сброшен мяч. Пусть события  , i=1,2,3 – состоят в том, что при i-м бросании мяч попадет в корзину. Выразить через , i=1,2,3 – состоят в том, что при i-м бросании мяч попадет в корзину. Выразить через  события: события:1) E – мяч попадет в корзину только при первом и третьем броске; 2) F – мяч попадет в корзину ровно один раз; 3) G – мяч попадет в корзину ровно два раза. 2. Для контроля продукции из трех партий деталей взята для испытания одна деталь. Как велика вероятность обнаружения бракованной продукции, если в одной партии 2/3 деталей бракованные, а в двух других все доброкачественные. 3. При приемном контроле из партии в 1000 штук изделий производится безвозвратная выборка в 50 штук. Найти вероятность того, что в выборке не окажется дефектных деталей, если во всей партии содержится 4 дефектных изделия. 4. На склад поступили электрические лампы трех партий. Известно, что в первой партии, состоящей из 400 штук, содержится 1 % нестандартных, во второй, состоящей из 500 штук, – 2 % нестандартных, и в третьей, состоящей из 100 штук, – 4 % нестандартных. Со склада лампы поступили в магазин и здесь оказались расположенными случайным образом. Определить вероятность того, что покупатель, берущий одну лампу, купит нестандартную. 5. Найти математическое ожидание и дисперсию случайной величины X, равной числу очков при одном бросании игральной кости. 6. Вычислительная машина производит n=108 одинаковых и независимых операций, в каждой из которых с вероятностью 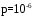 происходит ошибка. Каково среднее число ошибок? происходит ошибка. Каково среднее число ошибок?7. Дан статистический ряд: 3, 5, 7, 1, Y, Z, M, 7, 9, 10, 2, 3, 4, M, 7, 8, 9, 6, Y, 10, 12, 1, 2, 6, Z, 8, 15, 3, 2, 6, 8, Y, 16, 1, 6, 19, 4, 6, Y, 5, 20, 11, M, 13, 17, 5, Z, 13, 9, 14, 18, 7, 3, 2, 8, 20, M, 19, 1, 5, 8, 9, 3, 2, 17, Y, Z, M, 2, 19, 4, 7, 8, 3, 20, 1, 14, 9, 5, 15, 17, 3, 13, 2, 8, 6, 7, 4, 11, 1, 3, 7, 5, 8, 10, 18, 12, 17, 3, 5 а) составить ранжированный ряд б) составить вариационный ряд в) составить полигон распределения ряда г) составить гистограмму частот ряда д) составить эмпирическую функцию распределения е) найти выборочную среднюю ж) найти выборочную дисперсию Вариант 13 1. По мишени будет сделано три выстрела. Пусть событие  – при i -м выстреле произойдет попадание в мишень. – при i -м выстреле произойдет попадание в мишень.а) описать пространство элементарных событий этого опыта; б) выразить через  события: события:A – произойдет три попадания; B – не будет ни одного попадания; C – будет хотя бы одно попадание. 2. В урне содержатся 6 белых и 4 черных шара. Из урны наугад берут 2 шара. Какова вероятность того, что они окажутся одного цвета? 3. Радист трижды вызывает корреспондента. Вероятность того, что будет принят первый вызов, равна 0,2, второй – 0,3 и третий – 0,4. По условию приема, события, состоящие в том, что данный вызов будет услышан, независимы. Найти вероятность того, что корреспондент вообще услышит вызов. 4. С первого автомата получают на сборку 80 %, а со второго – 20 % одних и тех же деталей. На первом автомате брак составляет 1 %, а на втором – 4 %. Проверенная деталь оказалась бракованной. Определить вероятность того, что эта деталь изготовлена: 1) на первом автомате; 2) на втором автомате. 5. Случайная величина X задана плотностью распределения: 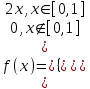 Найти математическое ожидание случайной величины. 6. Радиостанция ведет передачу информации в течение 10 мм/с. Работа происходит при наличии хаотической импульсной помехи, среднее число импульсов которой в одну секунду составляет 104. Для срыва передачи достаточно попадания одного импульса помехи в период работы станции. Считая, что число импульсов, попадающих в данный интервал времени, распределено по закону Пуассона, найти вероятность срыва передачи информации. 7. Дан статистический ряд: 3, 5, 7, 1, Y, Z, M, 7, 9, 10, 2, 3, 4, M, 7, 8, 9, 6, Y, 10, 12, 1, 2, 6, Z, 8, 15, 3, 2, 6, 8, Y, 16, 1, 6, 19, 4, 6, Y, 5, 20, 11, M, 13, 17, 5, Z, 13, 9, 14, 18, 7, 3, 2, 8, 20, M, 19, 1, 5, 8, 9, 3, 2, 17, Y, Z, M, 3, 19, 4, 7, 8, 3, 20, 1, 14, 9, 5, 15, 17, 3, 13, 2, 8, 6, 7, 4, 11, 1, 3, 7, 5, 8, 10, 18, 12, 17, 3, 5 а) составить ранжированный ряд б) составить вариационный ряд в) составить полигон распределения ряда г) составить гистограмму частот ряда д) составить эмпирическую функцию распределения е) найти выборочную среднюю ж) найти выборочную дисперсию Вариант 14 1. Взятая наудачу деталь может оказаться либо первого (событие A), либо второго (событие B), либо третьего (событие C) сорта. Что представляют собой события A+B, 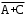 , AB, AB+C? , AB, AB+C?2. Имеется 10 карточек, на которых написаны числа: 3,3,3,4,4,5,5,6,6,6. Берутся одна за другой две из этих карточек. Число, написанное на первой карточке, принимают за числитель, на второй – за знаменатель дроби. Найти вероятность того, что полученная дробь будет правильной. 3. Производится стрельба по некоторой цели, вероятность попадания в которую при одном выстреле равна 0,2. Стрельба прекращается при первом попадании. Найти вероятность того, что произведено ровно 6 выстрелов. 4. По данным переписи 1951 года в Англии и Уэльсе среди отцов, имеющих сыновей, оказалось 13 % темноглазых и 87 % светлоглазых. У темноглазых отцов оказалось 39 % темноглазых и 61 % светлоглазых сыновей. У светлоглазых отцов – 10 % темноглазых и 90 % светлоглазых сыновей. Какова вероятность того, что наугад выбранные среди населения отец и сын имеют одинаковый цвет глаз. 5. Случайная величина |
