Контрольная работа (35 вариантов) Теория вероятностей и математическая статистика
 Скачать 289.78 Kb. Скачать 289.78 Kb.
|
X задана функцией распределения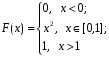 Найти плотность распределения и математическое ожидание случайной величины X. 6. Найти математическое ожидание числа лотерейных билетов, на которые выпадут выигрыши, если приобретено 200 билетов, причем вероятность выигрыша равна 0,001. 7. Дан статистический ряд: 3, 5, 7, 1, Y, Z, M, 7, 9, 10, 2, 3, 4, M, 7, 8, 9, 6, Y, 10, 12, 1, 2, 6, Z, 8, 15, 3, 2, 6, 8, Y, 16, 1, 6, 19, 4, 6, Y, 5, 20, 11, M, 13, 17, 5, Z, 13, 9, 14, 18, 7, 3, 2, 8, 20, M, 19, 1, 5, 8, 9, 3, 2, 17, Y, Z, M, 4, 19, 4, 7, 8, 3, 20, 1, 14, 9, 5, 15, 17, 3, 13, 2, 8, 6, 7, 4, 11, 1, 3, 7, 5, 8, 10, 18, 12, 17, 3, 5 а) составить ранжированный ряд б) составить вариационный ряд в) составить полигон распределения ряда г) составить гистограмму частот ряда д) составить эмпирическую функцию распределения е) найти выборочную среднюю ж) найти выборочную дисперсию Вариант 15 1. Взятая наудачу деталь может оказаться либо первого (событие A), либо второго (событие B), либо третьего (событие C) сорта. Что представляют собой следующие события: A+C, 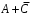 , , 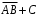 ? ?2. На 6 карточках написаны буквы: А,В,К,М,С,О. После перетасовки вынимают наугад одну карточку за другой и раскладывают их слева направо одна за другой в порядке вынимания. Найти вероятность того, что на карточках будет написано слово МОСКВА. 3. Два стрелка, для которых вероятности попадания в мишень равны соответственно 0,7 и 0,8 , производят по одному выстрелу. Определить вероятность хотя бы одного попадания в мишень. 4. В электрическую цепь последовательно включены 3 элемента, работающие независимо друг от друга. Вероятности отказов 1, 2 и 3 элементов соответственно равны: 0,1; 0,15 и 0,2. Найти вероятность того, что тока в цепи не будет. 5. Случайная величина X задана функцией распределения 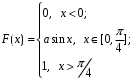 Найти коэффициент a, вероятность попадания величины X в интервал 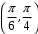 . .6. Найти вероятность попадания в интервал (6,10) нормально распределенной случайной величины X с 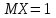 и и 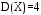 . .7. Дан статистический ряд: 3, 5, 7, 1, Y, Z, M, 7, 9, 10, 2, 3, 4, M, 7, 8, 9, 6, Y, 10, 12, 1, 2, 6, Z, 8, 15, 3, 2, 6, 8, Y, 16, 1, 6, 19, 4, 6, Y, 5, 20, 11, M, 13, 17, 5, Z, 13, 9, 14, 18, 7, 3, 2, 8, 20, M, 19, 1, 5, 8, 9, 3, 2, 17, Y, Z, M, 5, 19, 4, 7, 8, 3, 20, 1, 14, 9, 5, 15, 17, 3, 13, 2, 8, 6, 7, 4, 11, 1, 3, 7, 5, 8, 10, 18, 12, 17, 3, 5 а) составить ранжированный ряд б) составить вариационный ряд в) составить полигон распределения ряда г) составить гистограмму частот ряда д) составить эмпирическую функцию распределения е) найти выборочную среднюю ж) найти выборочную дисперсию Вариант 16 1. Пусть шесть охотников увидят лису и одновременно выстрелят по ней. Используя алгебру событий, выразить события: A – лиса будет убита и 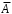 – лиса не будет убита - через события: – лиса не будет убита - через события:  – i-й охотник попал в цель (i=1,2,3,4,5,6). Попадание в лису равносильно ее убиению. – i-й охотник попал в цель (i=1,2,3,4,5,6). Попадание в лису равносильно ее убиению.2. На 32 карточках написаны по одной из 32 букв алфавита. Вынимаются наугад одна за другой три карточки и раскладываются слева на право в порядке появления. Найти вероятность того, что получилось слово "ТИР". 3. Вероятность того, что каждый из трех друзей придет в условленное место, равна соответственно: 0,8; 0,4; 0,7. Определить вероятность того, что встреча состоится, если для этого достаточно явиться двум из трех друзей. 4. На сборку поступают детали с трех автоматов. Первый дает 25 %, второй – 30 %, третий – 45 % деталей данного типа, поступающих на сборку. Первый автомат допускает 0,1 % брака, второй – 0,2 %, третий – 0,3 %. Найти вероятность поступления на сборку бракованных деталей. 5. Случайная величина X задана функцией распределения 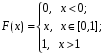 Найти дисперсию случайной величины X. 6. Устройство состоит из 1000 элементов, работающих независимо один от другого. Вероятность отказа любого элемента в течение времени t равна 0,002. Найти вероятность того, что за время t откажут ровно 2 элемента. 7. Дан статистический ряд: 3, 5, 7, 1, Y, Z, M, 7, 9, 10, 2, 3, 4, M, 7, 8, 9, 6, Y, 10, 12, 1, 2, 6, Z, 8, 15, 3, 2, 6, 8, Y, 16, 1, 6, 19, 4, 6, Y, 5, 20, 11, M, 13, 17, 5, Z, 13, 9, 14, 18, 7, 3, 2, 8, 20, M, 19, 1, 5, 8, 9, 3, 2, 17, Y, Z, M, 6, 19, 4, 7, 8, 3, 20, 1, 14, 9, 5, 15, 17, 3, 13, 2, 8, 6, 7, 4, 11, 1, 3, 7, 5, 8, 10, 18, 12, 17, 3, 5 а) составить ранжированный ряд б) составить вариационный ряд в) составить полигон распределения ряда г) составить гистограмму частот ряда д) составить эмпирическую функцию распределения е) найти выборочную среднюю ж) найти выборочную дисперсию Вариант 17 1. Радиолокационная станция будет вести наблюдения за k объектами. Событие  , i=1,..,k – будет потерян i-й объект. Используя алгебру событий, выразить через , i=1,..,k – будет потерян i-й объект. Используя алгебру событий, выразить через  следующие события: следующие события:A – ни один объект не будет потерян, B – будет потеряно не менее одного объекта, C – будет потеряно не более одного объекта. 2. В урне содержатся 6 белых и 4 черных шара. Из урны наугад берут 3 шара. Какова вероятность того, что они окажутся одного цвета? 3. Будет произведено девять независимых испытаний, в каждом из которых вероятность появления события A равна 0,1. Найти вероятность того, что событие A появится хотя бы два раза. 4. В первом ящике деталей первого сорта 30 %, во втором – 40 %. Из каждого ящика вынимается по одной детали. Определить вероятность того, что обе детали первого сорта. 5. Случайная величина X задана функцией распределения 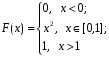 Найти дисперсию случайной величины X. 6. По каналу связи передается 1000 знаков. Каждый знак может быть искажен независимо от остальных с вероятностью 0,005. Найти приближенное значение вероятности того, что будет искажено не более трех знаков. 7. Дан статистический ряд: 3, 5, 7, 1, Y, Z, M, 7, 9, 10, 2, 3, 4, M, 7, 8, 9, 6, Y, 10, 12, 1, 2, 6, Z, 8, 15, 3, 2, 6, 8, Y, 16, 1, 6, 19, 4, 6, Y, 5, 20, 11, M, 13, 17, 5, Z, 13, 9, 14, 18, 7, 3, 2, 8, 20, M, 19, 1, 5, 8, 9, 3, 2, 17, Y, Z, M, 7, 19, 4, 7, 8, 3, 20, 1, 14, 9, 5, 15, 17, 3, 13, 2, 8, 6, 7, 4, 11, 1, 3, 7, 5, 8, 10, 18, 12, 17, 3, 5 а) составить ранжированный ряд б) составить вариационный ряд в) составить полигон распределения ряда г) составить гистограмму частот ряда д) составить эмпирическую функцию распределения е) найти выборочную среднюю ж) найти выборочную дисперсию Вариант 18 1. Прибор состоит из n блоков. Если выйдет хотя бы один блок из строя, то выйдет из строя весь прибор. Блоки выходят из строя независимо друг от друга. Используя алгебру событий, записать событие A – выход прибора из строя – через события 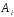 – выход из строя i- го прибора. – выход из строя i- го прибора.2. Вероятность того, что деталь имеет брак, равна 0,01. Какова вероятность того, что в партии из 10 деталей будет 3 бракованных детали? 3. Вероятность безотказной работы блока, входящего в систему в течение заданного времени, составляет 0,8. Для повышения надежности устанавливают такой же резервный блок. Требуется найти вероятность безотказной работы системы с учетом резервного блока. 4. Рабочий обслуживает 3 станка. Вероятность того, что в течении часа первый станок не потребует внимания рабочего, равна 0,95, для второго станка – 0,85, для третьего – 0,65. Какова вероятность того, что в течение часа хотя бы один станок не потребует внимания рабочего? 5. Найти неизвестное 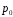 и дисперсию случайной величины, распределенной по закону и дисперсию случайной величины, распределенной по закону
6. Измерительный прибор имеет систематическую ошибку 5м и среднюю квадратическую ошибку 75м. Какова вероятность того, что ошибка измерения не превзойдет по абсолютной величине 5м? 7. Дан статистический ряд: 3, 5, 7, 1, Y, Z, M, 7, 9, 10, 2, 3, 4, M, 7, 8, 9, 6, Y, 10, 12, 1, 2, 6, Z, 8, 15, 3, 2, 6, 8, Y, 16, 1, 6, 19, 4, 6, Y, 5, 20, 11, M, 13, 17, 5, Z, 13, 9, 14, 18, 7, 3, 2, 8, 20, M, 19, 1, 5, 8, 9, 3, 2, 17, Y, Z, M, 8, 19, 4, 7, 8, 3, 20, 1, 14, 9, 5, 15, 17, 3, 13, 2, 8, 6, 7, 4, 11, 1, 3, 7, 5, 8, 10, 18, 12, 17, 3, 5 а) составить ранжированный ряд б) составить вариационный ряд в) составить полигон распределения ряда г) составить гистограмму частот ряда д) составить эмпирическую функцию распределения е) найти выборочную среднюю ж) найти выборочную дисперсию Вариант 19 1. Будет произведено наблюдение за группой, состоящей из четырех однородных объектов. Каждый из них за время наблюдения может быть обнаружен или не обнаружен. Рассмотрим события: A – будет обнаружен ровно один из четырех объектов; B – будет обнаружен хотя бы один объект; C – будет обнаружено не менее двух объектов; D – будет обнаружено ровно два объекта; E – будет обнаружено ровно три объекта; F – обнаружены четыре объекта. Указать, каково значение событий A+B, AB, B+C, BC, D+E+F. 2. В урне 2 белых, 3 черных и 5 красных шаров. Наугад вынимают три пары шаров. Найти вероятность того, что среди вынутых шаров хотя бы два будут разного цвета. 3. Произведено 9 независимых испытаний, в каждом из которых вероятность появления события A равна 0,1. Найти вероятность того, что событие A появится хотя бы два раза. 4. Вероятность удовлетворять стандарту для изделия некоторого производства равна 0,96. Была предложена упрощенная система контроля изделия, дающая положительный результат с вероятностью 0,98 для изделий, удовлетворяющих стандарту, и с вероятностью 0,05 для изделий, не удовлетворяющих стандарту. Какова вероятность того, что изделие, выдержавшее это испытание, удовлетворяет стандарту? 5. Найти значение C и 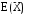 случайной величины X, обладающей плотностью распределения: случайной величины X, обладающей плотностью распределения: 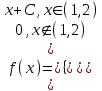 6. Будут произведены измерения партий деталей без систематических погрешностей. Случайные погрешности измерения подчинены нормальному закону со среднеквадратическим отклонением 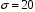 . Найти вероятность того, что измерение будет произведено с погрешностью, не превосходящей по абсолютной величине 4. . Найти вероятность того, что измерение будет произведено с погрешностью, не превосходящей по абсолютной величине 4.7. Дан статистический ряд: 3, 5, 7, 1, Y, Z, M, 7, 9, 10, 2, 3, 4, M, 7, 8, 9, 6, Y, 10, 12, 1, 2, 6, Z, 8, 15, 3, 2, 6, 8, Y, 16, 1, 6, 19, 4, 6, Y, 5, 20, 11, M, 13, 17, 5, Z, 13, 9, 14, 18, 7, 3, 2, 8, 20, M, 19, 1, 5, 8, 9, 3, 2, 17, Y, Z, M, 9, 19, 4, 7, 8, 3, 20, 1, 14, 9, 5, 15, 17, 3, 13, 2, 8, 6, 7, 4, 11, 1, 3, 7, 5, 8, 10, 18, 12, 17, 3, 5 а) составить ранжированный ряд б) составить вариационный ряд в) составить полигон распределения ряда г) составить гистограмму частот ряда д) составить эмпирическую функцию распределения е) найти выборочную среднюю ж) найти выборочную дисперсию Вариант 20 1. Будет произведено три выстрела по мишени. Рассматриваются события  - попадание в мишень при i-м выстреле (i=1,2,3). Представить в виде сумм, произведений или сумм произведений событий - попадание в мишень при i-м выстреле (i=1,2,3). Представить в виде сумм, произведений или сумм произведений событий  и и 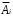 следующие события: следующие события:A – все три попадания; B – все три промаха; C – хотя бы одно попадание; D – хотя бы один промах; E – не меньше двух попаданий; F – не более одного попадания. 2. В партии из 100 изделий имеется 6 нестандартных. Наугад изымают 10 изделий. Определить вероятность того, что среди 10 изделий будет 2 нестандартных. 3. Три электрические лампочки будут последовательно включены в цепь. Вероятность того, что одна лампочка перегорит, если напряжение в сети превысит нормальное, равна 0,6. Найти вероятность того, что при повышенном напряжении тока в цепи не будет. 4. В трех урнах имеются белые и черные шары. В первой урне 3 белых и 1 черный шар, во второй – 6 белых и 4 черных, в третьей – 9 белых и 1 черный. Из наудачу взятой урны извлекается шар. Найти вероятность того, что он белый. 5. Найти математическое ожидание и дисперсию случайной величины X, распределенной по закону:
6. Случайная величина X распределена нормально со среднеквадратическим отклонением 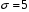 . Найти длину интервала, в который с вероятностью 0,9973 попадет X в результате испытания. . Найти длину интервала, в который с вероятностью 0,9973 попадет X в результате испытания.7. Дан статистический ряд: 3, 5, 7, 1, Y, Z, M, 7, 9, 10, 2, 3, 4, M, 7, 8, 9, 6, Y, 10, 12, 1, 2, 6, Z, 8, 15, 3, 2, 6, 8, Y, 16, 1, 6, 19, 4, 6, Y, 5, 20, 11, M, 13, 17, 5, Z, 13, 9, 14, 18, 7, 3, 2, 8, 20, M, 19, 1, 5, 8, 9, 3, 2, 17, Y, Z, M, 2, 19, 4, 7, 8, 3, 20, 1, 14, 9, 5, 15, 17, 3, 13, 2, 8, 6, 7, 4, 11, 1, 3, 7, 5, 8, 10, 18, 12, 17, 3, 5 а) составить ранжированный ряд б) составить вариационный ряд в) составить полигон распределения ряда г) составить гистограмму частот ряда д) составить эмпирическую функцию распределения е) найти выборочную среднюю ж) найти выборочную дисперсию Вариант 21 1. Подбрасываются две монеты. Рассмотрим следующие события: A – появление герба на первой монете; B – появление цифры на первой монете; C – появление герба на второй монете; D – появление цифры на второй монете; E – появление хотя бы одного герба; F – появление хотя бы одной цифры; G – появление одного герба и одной цифры; H – не появление герба ни на одной монете; K – появление двух гербов. Определить каким событиям этого списка равносильны следующие события: A+C, AC, EF, G+E, GE, BD, E+K? 2. В партии, состоящей из 100 изделий, среди которых имеется 10 бракованных, будут выбраны случайным образом 5 изделий для проверки качества. Найти вероятность того, что среди выбранных изделий одно стандартное. 3. Три прибора включены в сеть параллельно. Известны вероятности безотказной работы приборов за время T: 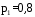 , , 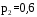 , ,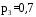 . Найти вероятность того, что цепь за время T прервется. . Найти вероятность того, что цепь за время T прервется.4. Самолеты состоят из трех уязвимых частей. Для вывода самолета из строя достаточно одного попадания в первую часть или двух попаданий во вторую часть, или трех попаданий в третью. Два снаряда попали в самолет. Найти вероятность вывода самолета из строя, если вероятность попадания одного снаряда в первую часть равна 0,18, во вторую – 0,30, в третью – 0,56. 5. Найти дисперсию случайной величины X, распределенной по закону:
6. Цена деления шкалы измерительного прибора равна 0,2. Показания прибора округляют до ближайшего целого деления. Найти вероятность того, что при отсечении будет сделана ошибка, меньшая 0,03. 7. Дан статистический ряд: 3, 5, 7, 1, Y, Z, M, 7, 9, 10, 2, 3, 4, M, 7, 8, 9, 6, Y, 10, 12, 1, 2, 6, Z, 8, 15, 3, 2, 6, 8, Y, 16, 1, 6, 19, 4, 6, Y, 5, 20, 11, M, 13, 17, 5, Z, 13, 9, 14, 18, 7, 3, 2, 8, 20, M, 19, 1, 5, 8, 9, 3, 2, 17, Y, Z, M, 1, 19, 4, 7, 8, 3, 20, 1, 14, 9, 5, 15, 17, 3, 13, 2, 8, 6, 7, 4, 11, 1, 3, 7, 5, 8, 10, 18, 12, 17, 3, 5 а) составить ранжированный ряд б) составить вариационный ряд в) составить полигон распределения ряда г) составить гистограмму частот ряда д) составить эмпирическую функцию распределения е) найти выборочную среднюю ж) найти выборочную дисперсию Вариант 22 1. Завод выпускает изделия определенного вида, каждое изделие может иметь или не иметь дефект. После изготовления каждое изделие осматривается |
